基于ICA 的多通道低频振荡模式识别方法

王冬云，张建刚，陈继刚

(1.秦皇岛职业技术学院机电工程系,河北 秦皇岛 066100；2.秦皇岛首秦金属材料有限公司,河北 秦皇岛 066100；3.燕山大学机械工程学院,河北 秦皇岛 066100)

随着电力系统互联程度的加强,以及源-荷的不确定因素,如大量风、光等新能源的并网,以及空调、电动汽车等柔性负荷的不断加入,给电网带来了一定的冲击,对系统安全造成了一定的威胁[1-2]。同时,随着广域测量系统(Wide Area Measurement System,WAMS)的使用,实现了电网信息数据的可观、可测,给低频振荡模式辨识提供了很好的条件。

低频振荡模式辨识方法主要可以分为基于数值解的分析方法及基于实测信号的分析方法。基于数值解的分析方法目前主要有传递函数法、时域仿真法、非线性理论法。传递函数法使用反馈信号寻找系统间相对应的传递关系,根据传递函数频率响应方法,准确计算低频振荡主导模式的特征值[3]。时域仿真法一般是利用共轭梯度法或不变子空间法用在电力系统的并行计算[4-5]。非线性理论法中比较常见的为模态级数法,基于泰勒展开式求解,能够用线性变换近似求解非线性系统封闭解,有着计算量较小的优势[6-7]。

基于实测信号的分析法不依靠系统模型的准确度且不用复杂的计算过程,可以基于WAMS 系统进行分析。当前较多使用的方法有Prony 法、HHT、小波变换等。Prony 算法在含有较低噪声时对低频振荡模式辨识有着较高的辨识精度[8-9]；小波变换具有多分辨分析的特点,但存在小波基函数难以选取的难题[10]。希尔伯特黄变换(Hilbert-Huang Transform,HHT) 是通过使用经验模态分解算法(Empirical Mode Decomposition,EMD),将复杂的振荡信号分解成多个固有模态函数(Intrinsic Mode Function,IMF)集合,在此基础上再对所有IMF 分量进行Hilbert 变换得到振荡参数,在低频振荡中有着较好的应用[11-12],但存在模态混叠及边界效应的问题。

大多数低频振荡模式辨识方法研究是基于单通道的低频振荡信号展开,对于多通道低频振荡信号研究相对较少。基于多通道信号的方法节省了辨识所有振荡模式需要的时间,提高了辨识精度,同时能够更好地满足电网的现状分析,为低频振荡分析提供更多参考信息。NezamSarmadi S A[13]、Ghasemi H[14]等将奇异谱分解(Singular Spectrum Decomposition,SSD)应用于电力系统机电振荡模式识别,对多通道振荡信号进行模式辨识,但是此种方法中存在要对较大矩阵进行奇异值分解的弊端,计算速度较慢,计算复杂。

利用独立分量算法(Independent Component Algorithm,ICA)[15]在分离多通道信号中的优势,将其引入多通道低频振荡信号分离中。由于ICA 能够分离信号的同时,也可分离噪声,因此将其与Prony 法结合,提取多通道低频振荡模式,并通过数值仿真对所提算法辨识精度、时间等方面进行分析,结果表明,与直接利用单通道信号算法进行辨识相比,所提ICA-Prony 法在抗噪性、计算速度上有着明显的优势,并且更加简单。

1 ICA 算法

1.1 ICA 分离模型

ICA 是由盲源信号分离方法(Blind Signal Separation,BSS)扩展而来,该方法重点就是如何从多通道混合信号中完整分离出每个信号,即源信号。如果混合信号系统是己知,那么此方法即为简单的混合矩阵求逆操作。具体如图1 所示:

图1 ICA 信号分离

1.2 ICA 数学模型

在分析多通道信号的传输通道不同的基础上,发现信号主要的混合方式主要有线性、卷积、非线性混合等。电网中基于WAMS 采集到的信号是经过上述混合方式混合的多通道信号,在对其多通道信号进行振荡模式辨识之前需要采用不同的方法进行分离。ICA 可以分离线性、非线性多通道低频振荡信号,并且由于在实际的电网环境中,会包含噪声,而ICA 算法可以将噪声看作是混合信号而被分离出来,从而达到去噪的目的。

多通道低频振荡信号模型可以用式(1)表示:

式中:A是M×M混合矩阵；矩阵S的列是未知源独立信号s1(t),s2(t),…,sM(t)；矩阵X的列包括多通道电力系统低频振荡持续信号估计值。

在利用ICA 分离多通道信号过程中,要建立解混矩阵W,使yi(t)与Si(t)无限接近,同时使得输出的任意两个信号yi和yj不相关,即通过矩阵W对y(t)进行线性变换,具体表达式为:

式中:W=[W1,W2,…,WM]为解混矩阵。

在分离过程中,要使得y(t)尽可能非高斯化,从而提高多通道信号分离准确率。对于矩阵W,需要通过对源信号去均值、初始化、及归一化等处理,达到优化选择各权重Wi的目的,从而求得多通道振荡源信号分离出的各通道估计值yi,i=1,…,M,如下所示:

式中:θj为相位,Aj为幅值；αj为衰减因子；fj为振荡频率；M为模态数。

首先对多通道信号标准化去均值、白化,消除信号之间的相关性。去均值:信号要满足E(xi)=0,=1；

在上述对信号白化处理后,观察混合信号x变成白化矢量Z；可通过对随机矢量X的协方差矩阵进行奇异值分解,如下:

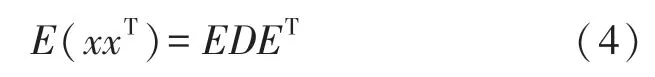
D为球化矩阵,得到白化矢量

设置初始权重矢量Wi,满足‖Wi‖2=0；并行批量迭代是将yi=代入优化方程。E{·}是求均值；g(·)代表非线性函数,取非线性函数g(x)=x*exp(-x2/2),g′代表非线性函数的导数。

在此基础上,需要对Wi归一化处理:,迭代归一化后,若｜Wi(k＋1)｜＜ξ,收敛误差0＜ξ＜1,则算法收敛,继续Wi代入Y=WX得到各个单通道的低频振荡源信号的估计值,否则继续进行迭代,直到满足收敛条件。

2 基于ICA-Prony 的低频振荡模式辨识方法

Prony 变换的推导过程,在大量文献中已经进行了介绍[16-17],此处不再重点介绍。

Prony 算法是用一组指数项的线性组合来拟合分离后的振荡信号,并可以得到所需要的分离信号的频率,达到对低频振荡模式辨识的目标。

经过ICA 算法分离后的信号,拟合模型为:

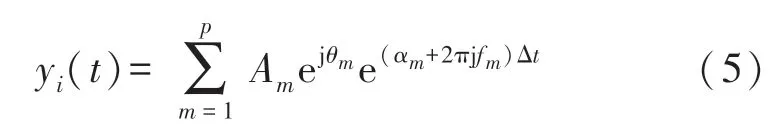
式中:p为模型的阶数,m为指数函数序号,取值为1,2,3,…,p。

假设zk是下式方程的齐次解:

式中:φ(z)为常系数线性差分方程,ai为特征方程的系数。将上式进行求解得到特征根zk,进而代回式(5)中,即可求解分离信号的频率,从而达到对信号低频振荡模式的辨识。

3 算例分析

为了验证所提方法的正确性,分别对含噪声的单通道信号以及多通道低频振荡信号进行仿真分析。

3.1 含噪声单通道信号分析

构建低频振荡信号表达式如下所示:

式中:n(t)为信噪比为3 的高斯白噪声。原始信号如图2 所示。

图2 含噪原始信号

利用ICA 算法对信号进行噪声分离,得到分离信号与原始信号对比图如图3 所示。

图3 分离信号与原始信号对比图

由上图可知,经ICA 分离噪声后的信号能够与原始信号较好地拟合,保留有原始信号的特征。再对其利用Prony 方法进行参数辨识,得到的结果如表1 所示。

表1 模式辨识结果

由表1 可以看出,在经过ICA 算法噪声分离后,能够准确地辨识低频振荡模式,辨识结果误差在3%以内,从而ICA 在分离噪声方面具有很好的效果,可以为后续参数辨识提供支撑。

3.2 多通道信号仿真分析

为了验证所提方法低频振荡辨识的正确性,构造含有3 个通道的混合低频振荡信号,各个通道的信号表达式为:

混合各个通道的波形如图4 所示。

图4 混合信号波形

首先对多通道混合信号利用ICA 算法进行分离,得到分离后的各个通道的波形如图5 所示。

图5 ICA 分离通道信号图

在得到各个通道信号的基础上,利用Prony 算法对分离后的信号进行低频振荡模式辨识,得到的结果如表2 所示。

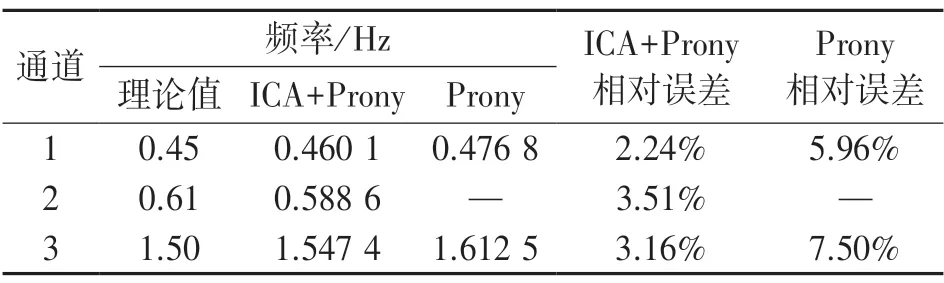
表2 多通道方法辨识结果

由图5 可知,在经过ICA 分离多通道混合信号后,能够正确地分出所含有的各个通道的信号,能够准确地分出多通道信号,能够较好地保留原有信号的特征,为后续低频振荡辨识提供基础。

由表2 可知,在使用该低频振荡结果时,精度较高,并且均能辨识出低频振荡模式,参数误差均在4%以内,能够体现出本方法的多通道并行效果。直接利用Prony 算法进行多通道信号辨识时,能够发现,存在遗漏通道2 的低频振荡模式的情况,得到的结果误差较大,无法准确对多通道信号进行分析。综上所述,ICA＋Prony 法能准确并快速地获取多通道低频振荡信号模式参数。

4 结论

提出了一种基于ICA＋Prony 法的多通道信号低频振荡模式辨识方法。首先将ICA 算法作为多通道分析手段,再利用Prony 法对分离后的通道信号进行低频振荡模式辨识。仿真分析表明,该方法利用ICA 算法进行噪声分离以及通道信号分离时,分离效果较好,能够较好地保留原始信号特征,为后续辨识提供支撑。与直接利用Prony 法的辨识结果相比,该方法辨识出的参数结果更加接近于理论值,相对误差均小于4%,且能够解决直接利用Prony 方法进行辨识时的模式遗漏问题,在多通道背景下,该方法中可一次性准确地给出多种振荡模式的辨识结果,因此在计算速度上也具有一定的优势。在后期将继续对多通道低频振荡辨识精度的提升、在线监测辨识,安全预警方面的问题进行研究。