基于Fluent有限元模拟的连续弯管冲蚀特性研究
2021-10-26陈泽陈国清杨先辉文宏武李阳付雪松
陈泽,陈国清,杨先辉,文宏武,李阳,付雪松
(1.大连理工大学材料科学与工程学院,辽宁大连 116085;2.中国石油集团渤海钻探油气井测试分公司,河北廊坊 065007)
0 引言
冲刷腐蚀是金属表面和腐蚀介质之间由于高速的相对运动所引发的损伤现象,它是冲刷和腐蚀共同作用的结果,因此又被称为冲蚀磨损,是一种具有强烈危害性的局部腐蚀[1]。管道系统在油气田开发和油气输送等场合应用广泛,在管道输送过程中其内部流体携带固体颗粒等杂质不断对管道内壁造成冲刷腐蚀,尤其在连续弯管处液体流向的持续改变更是加剧了冲蚀破坏程度。此外,冲蚀与管道材料和结构、内部液体流速及砂粒粒径等诸多因素都有关系[2-4]。鲁剑啸[5]采用正交试验方法分析得到90°弯管的冲蚀影响因素主次顺序为:入口流速>颗粒质量流量>弯径比>管道直径>颗粒粒径。闫宏伟等[6]对90°弯管的冲蚀进行模拟,结果表明不同因素对油气管道弯头冲蚀速率影响程度不同,其中入口速度和质量流量均对冲蚀速率具有正向促进作用。
综上,之前的研究都是基于单个弯管分析影响冲蚀现象的主要因素,而针对连续弯管的冲蚀磨损特性研究依然较为缺乏。本文运用Fluent有限元软件对连续弯管进行冲蚀磨损的数值模拟研究,分析讨论了液体流速和颗粒粒径对连续弯管冲蚀磨损的影响规律。
1 理论模型
1.1 离散相(DPM)模型
在流体与颗粒相组成的液固两相流体系中,流体相连续,而将内部颗粒作离散化处理,因此该模型被叫做离散相模型[7-8]。此模型为欧拉-拉格朗日模型,采用欧拉法描述了连续相,采用拉格朗日方法描述了离散相,并且对大量粒子的运动方程进行积分得到了颗粒相的运动轨迹,如下所示:

1.2 冲蚀磨损模型
连续弯管内壁面的冲蚀磨损示意图如图1所示。由于流动是连续的,颗粒的冲击会造成材料表面产生冲击坑,并且当冲击后形成的切削废料堆积到一定程度时会附着在冲击坑附近的内壁面上,从而能够相对阻挡后续颗粒的进一步冲击。
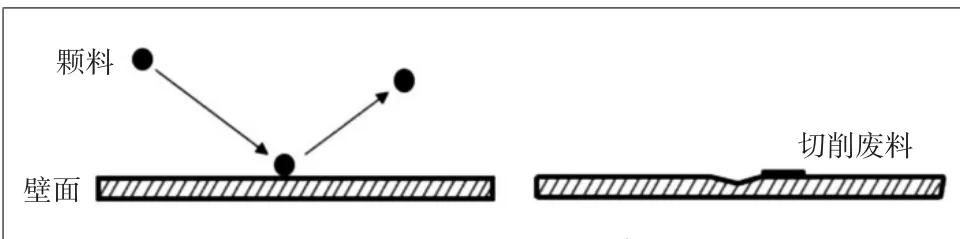
图1 连续弯管内壁面冲蚀磨损示意图
将冲蚀磨损理论计算公式应用到连续弯管冲蚀磨损研究中,则弯管内壁面的冲蚀率可以通过下式进行计算[9]:

式中:Er为冲蚀率,kg/m2·s;mp为颗粒质量流量,kg/s;C(dp)为粒径函数;b(v)为颗粒碰撞速度函数;Aface为碰撞壁面面积,m2;f(α)为冲击角函数,冲击角线性分段函数如表1所示。
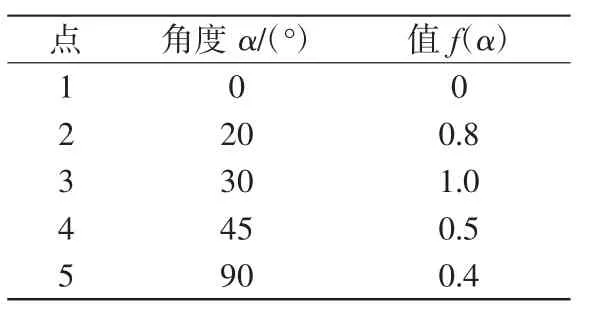
表1 冲击角线性分段函数[10]
2 连续弯管冲蚀过程的有限元模拟
2.1 模型及网格划分
图2是连续弯管内部流体域的有限元模型及流体划分网格。首先在SolidWorks软件中根据相应尺寸构建连续弯管的三维几何模型,再将其导入有限元模拟软件ANSYS Workbench中得到连续弯管的有限元模型,如图2(a)所示。然后对连续弯管进行网格划分,网格整体质量介于0.8~1.0,经检验网格满足无关性要求及计算需求,网格划分如图2(b)所示。
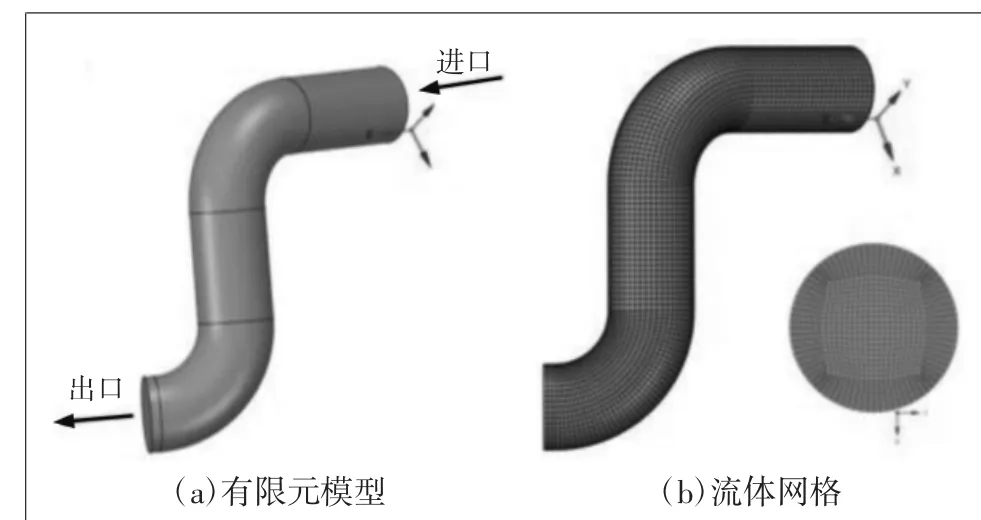
图2 连续弯管内部流体域的有限元模型及流体划分网格
2.2 边界条件
使用Fluent软件模拟计算管道内壁的冲蚀磨损率。首先,在Fluent中选用k-ε湍流模型,湍流强度为4%,采用速度入口,压力出口。此外,还需要分别对反弹系数、冲击角函数、粒径函数和速度指数函进行设置,其中粒径函数设置为常数1.8×10-9,速度指数函数设置为常数2.6。压力速度耦合使用SIMPLEC求解算法。
3 计算结果与分析
3.1 液体流速对连续弯管冲蚀的影响
为了研究连续弯管在不同流速下的冲蚀规律,在模拟过程中保持其他条件不变,选取流速大小分别为5、10、15、20、25、30 m/s,然后通过模拟获得不同流速的冲蚀率云图,如图3所示。可以看出,不同流速造成的最大冲蚀率不同,但冲蚀磨损的区域大致相同,主要存在两处区域:1)上弯头外拱壁;2)下弯头外拱壁右侧一道叶片状的狭窄区域。除此之外,连续弯管的上弯头冲蚀区域面积大,而下弯头外拱壁的损伤程度更大。这主要是因为固体颗粒由于离心力作用富集在弯头的外拱壁,当运动至下弯头时一方面由于涡旋造成冲蚀方向偏向一侧,另一方面势能降低导致速度增大,加剧了该处的磨损。
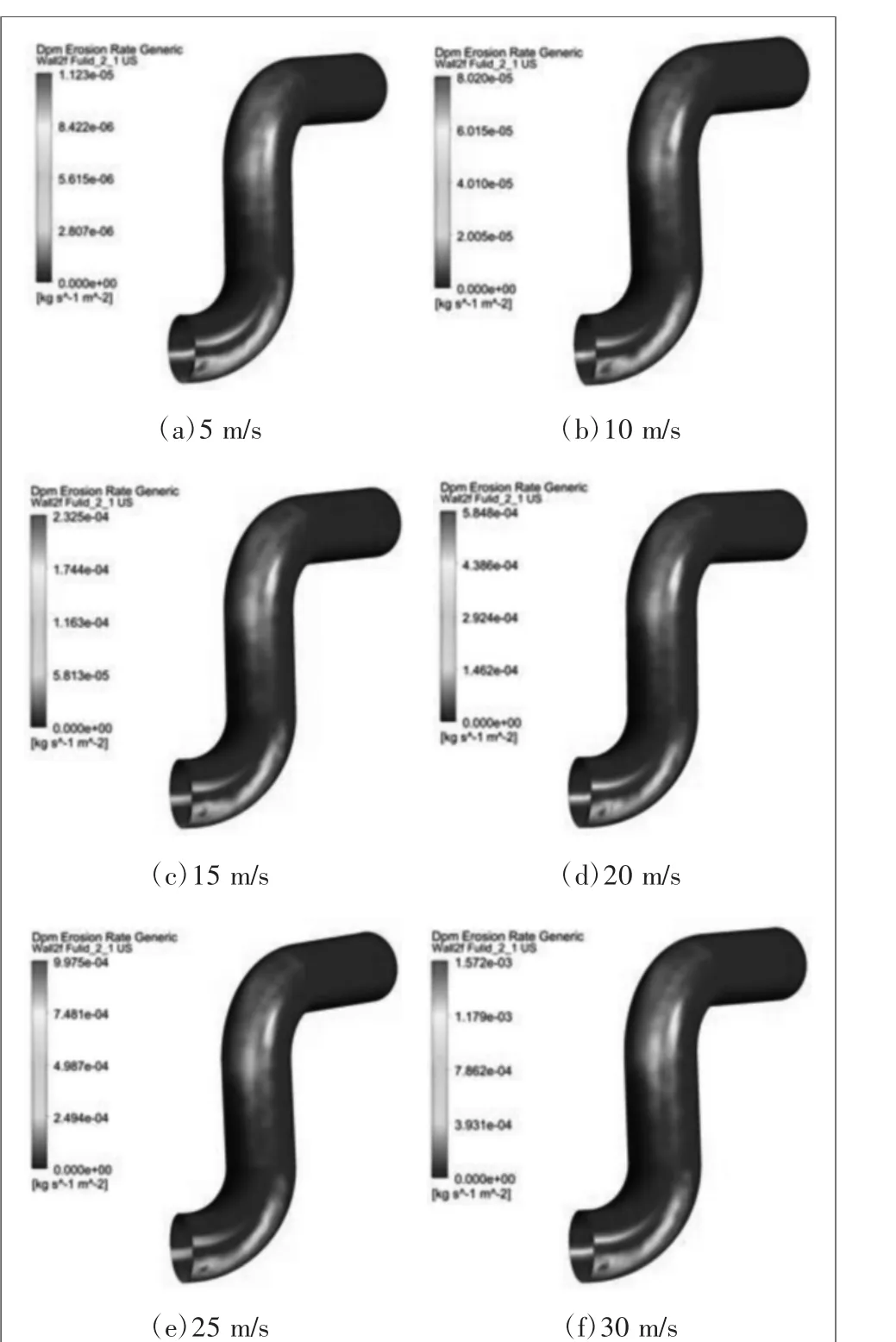
图3 不同流速的冲蚀率云图
图4所示为不同流速下最大冲蚀率与平均冲蚀率的变化曲线,可以看出当液体流速逐渐增大时,连续弯管最大冲蚀率及平均冲蚀率都相应增加,并且提升幅度也逐渐增大,满足ε= k·vn的表达式,经拟合其函数关系式分别为f(v)=0.003v2.569和g(v)=0.0005v2.648。这是因为流体所携带的固体颗粒在运动过程中由于速度增加会加剧对管道内壁的冲击切削,最终会造成壁面的磨损量加大,所以表现为冲蚀率的不断增大,且当液体流速增加至30 m/s 时,最大冲蚀率为1.57×10-3kg /(m2·s) 。
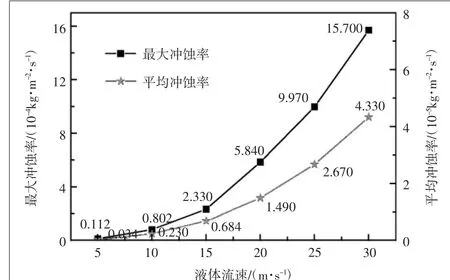
图4 不同流速下最大冲蚀率与平均冲蚀率的变化曲线
3.2 颗粒粒径对连续弯管冲蚀的影响
为了研究连续弯管内部流体携带不同尺寸颗粒时对壁面的冲蚀规律,在模拟过程中保持其他条件不变,选取颗粒粒径大小分别为0.05、0.10、0.20、0.40、0.60、0.80、1.00 mm,得到不同流速的冲蚀率云图如图5所示。可以看出,当粒径偏小时,管道的冲蚀较严重区域主要集中于上弯管的外拱壁面和下弯管的底侧壁面中心位置;随着粒径的不断增加,冲蚀区域逐渐向下弯管壁面的外侧转移。造成上述现象的原因主要是当粒径较小时,颗粒的惯性也较小,由于周围流体的包裹使得颗粒并未直接与入口段管道内壁接触,而是受转弯部位作用与上弯头的外拱壁面发生碰撞。但是当粒径逐渐增加时,颗粒质量相应增大,其惯性和动能也就越大,再加上重力与湍流涡旋共同作用,会导致颗粒以较快的速度在连续转弯处产生运动轨迹的偏移,从而体现为连续弯管冲蚀严重区域的偏移。

图5 不同颗粒粒径的冲蚀率云图
图6所示为不同颗粒粒径下最大冲蚀率与平均冲蚀率的变化曲线,可以看出:随着粒径的增加,连续弯管的平均冲蚀率先减小后趋于稳定,而最大冲蚀速率呈先减小后增大的变化趋势,且当颗粒粒径为0.2 mm 时最大冲蚀速率最小,为2.95×10-5kg /(m2·s)。前者是因为冲蚀区域发生了转移,下弯头冲蚀量的增加与上弯头冲蚀量的减少相对均衡,整体表现为平均冲蚀率的趋于稳定。而最大冲蚀率的变化主要是因为初期较小颗粒的质量小,由于流体黏度的影响,颗粒被外部流体所包裹从而减少了与壁面直接接触的可能性,同时也阻碍了后续颗粒对壁面的进一步冲蚀[11],体现为冲蚀率的减小。而当粒径增大到一定程度后,流体对固体颗粒的束缚力降低,固体颗粒与壁面发生碰撞的概率增大,颗粒对管道内壁的冲击切削能力增强,因此最大冲蚀率呈现出迅速提高的趋势。
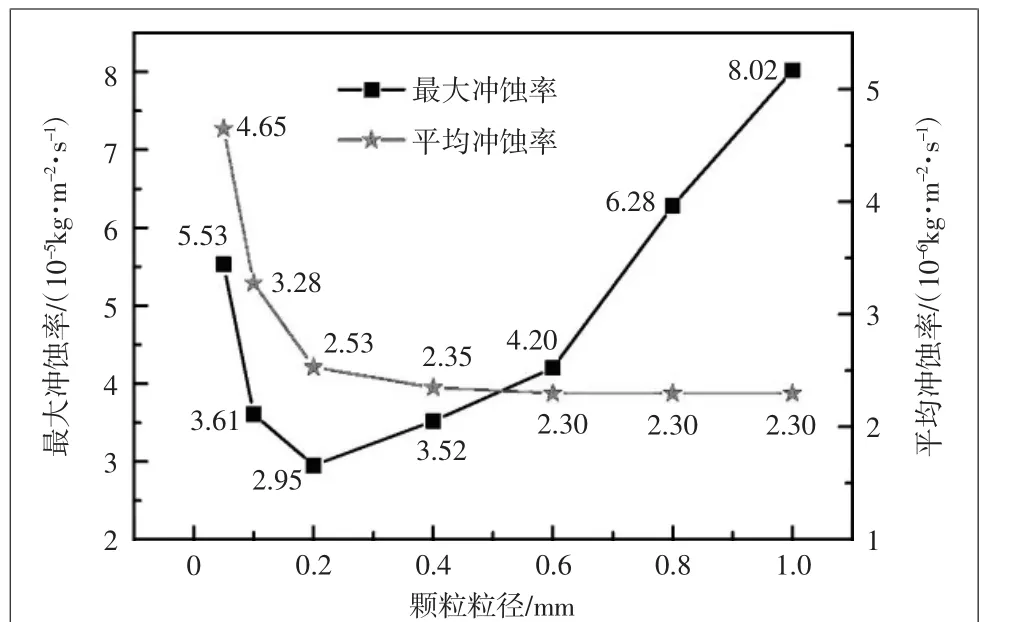
图6 不同颗粒粒径下最大冲蚀率与平均冲蚀率的变化曲线
4 结论
1)不同流速造成连续弯管壁面的冲蚀率大小不同,但冲蚀磨损的区域大致相同。当液体流速逐渐增大时,连续弯管最大冲蚀率及平均冲蚀率也都相应增加,并且提升幅度也逐渐增大。冲蚀率与流速之间呈指数关系,其函数关系式分别为f(v)=0.003v2.569和g(v)=0.0005v2.648。
2)随着粒径的不断增加,连续弯管的主要冲蚀区域由上弯管外拱逐渐向下弯管壁面的外侧转移,平均冲蚀率先减小后趋于稳定,而最大冲蚀速率呈先减小后增大的变化趋势,且当颗粒粒径为0.2 mm时最大冲蚀速率最小,其值为2.95×10-5kg /(m2·s)。
