基于GM-Markov模型的船舶水上交通安全综合指数预测研究

贾帅林，杜柏松，刘然，秦世云

（浙江海洋大学 船舶与海运学院，浙江 舟山 316022）

0 引言

船舶水上交通安全综合指数包括水上船舶交通事故数、沉船数、死亡失踪人数和直接经济损失4项标准，定量分析“4项指标”历史数据的变化趋势对保障船舶水上交通安全、明确设施建设方向以及控制水上交通风险具有重要意义[1]。灰色系统预测理论适用于“信息不完全”“数据样本少”等特点数据的问题预测，是预测船舶水上交通安全综合指数的主要方法。在解决水上船舶交通安全等实际生产问题时，国内外的很多学者钻研了灰色预测模型及其组合模型的应用。李玲玲等[2]利用水上交通事故数量的原始数据和灰色预测值的残差，建立了BP神经网络和灰色预测的组合模型。周涂强等[3]运用了蒙特卡洛仿真法改进灰色预测模型，利用风险概率分布的形式来反映区域内交通安全水平的实际变化趋势；船舶水上交通安全综合指数伴随复杂性、非线性和波动性等变化特征，而马尔科夫预测可以反映系统在不同状态下的转移规律，尤其能克服数据的波动性。因此，本文提出了一个GMMarkov模型, 运用马尔科夫原理改进灰色预测分析模型，以期提高预测精度。

1 GM-Markov预测模型

1.1 灰色GM(1.1)预测

最后，对式（1）所求得的预测值进行累减计算，可得灰色预测值：

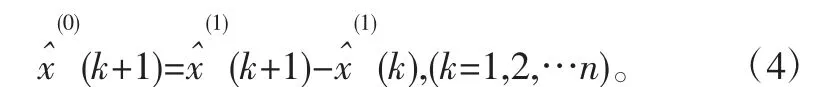
1.2 马尔科夫预测及GM-Markov模型的构建

将船舶水上交通预测值残差状态作为马尔科夫预测决策过程，并根据预测时间段内的残差状态之间的转移概率来预测其变化趋势，利用这个原理来修正灰色预测模型的预测值[5]。建模过程如下：

首先，根据灰色预测得到的预测值，计算灰色预测的残差：

其中，预测状态“高估”时候取“+”，“低估”时取“-”。

1.3 预测模型精度的检验

为更好地验证灰色预测模型和灰色马尔科夫模型的预测精度，分别对预测值进行相对误差（Q）检验、均方差比值（C）检验和小概率误差（P）检验，检验标准如表1。

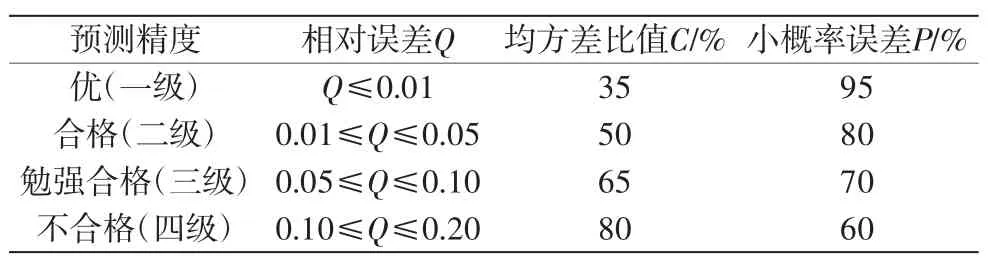
表1 预测精度等级划分标准

2 船舶水上交通安全综合指数预测的实证分析

2.1 灰色GM(1,1)模型预测

由我国交通运输部综合规划司公布的《交通运输行业发展统计公报》[6]，可查得2003—2019年船舶水上交通安全综合指数相关数据，如表2所示。可以看出4项指标总体变化趋势均呈下降态势，符合灰色预测对数据要求的特征，因此，采用传统的灰色预测模型进行预测。

表2 2003—2019年船舶水上交通安全综合指数

首先，以2004—2013年的水上交通事故数为原始序列，即X(0)={562，532，440，420，342，358，331，298，270,262}，根据式（2）～式（4）可知水上交通事故数的灰色预测模型为：x^(k+1)=-5929.2959·e-0.0882t+6491.2959，再对此进行累减计算，即可得出水上交通事故数的灰色预测值为x^(0)={562，500.6，458.3，419.6，384.2，351.8，322.1，294.9，270,247.2}，同样的预测方法，求得死亡失踪人数、沉船数和直接经济损失的灰色预测值，如表5所示。

从预测结果看：4项指标整体呈下降态势，基本能够从整体上反映水上交通安全4项指标的变化趋势；但通过观察各拟合曲线发现（如图1），灰色预测模型的拟合程度较差，只能反映出整体的变化趋势。根据精度分析标准该预测模型的精度标准仅为“合格”，说明模型的预测精度有欠缺。

鉴于此，本文利用马尔科夫模型对灰色预测值进行修正，希望能提高水上交通安全综合指数的预测精度。

2.2 GM-Markov预测

仍然以水上交通事故数这一指标为例，结合马尔科夫原理进一步优化灰色预测值[7]。由上述建模过程，可确定2004—2013年水上交通事故数的状态分布情况。

根据水上交通事故数的相对误差序列得到4个状态的分布情况，得到状态的一步转移概率矩阵如下：

多步状态转移概率矩阵：p(n)=［p(1)］(n)。

根据马尔科夫预测的转移概率矩阵的原理，以2014年最近的4个年份作为水上交通事故数的状态预测的原始数据，根据对应年份的状态和转移步骤[8]，计算出水上交通事故数量的累积状态转移概率，如表3所示，因此取累积状态转移概率最大的状态4作为2014年可能的状态，根据式（8）可得2014年的预测值。

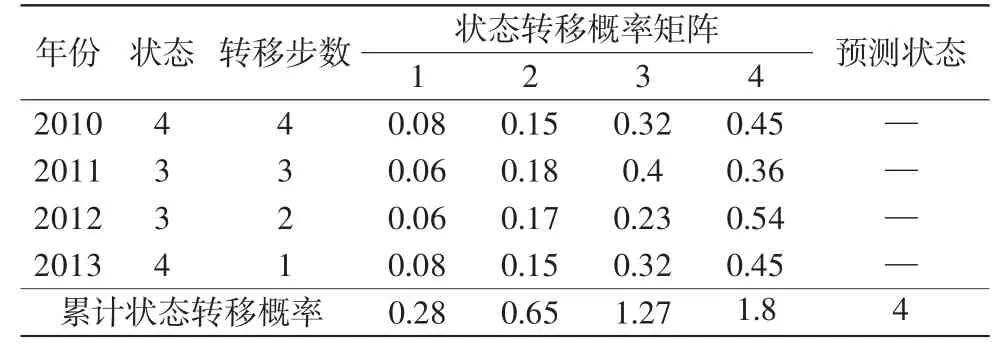
表3 2014年水上交通事故数状态预测

同理，可得到死亡失踪人数、沉船数和直接经济损失3项指标的状态划分结果，以及2014年船舶水上交通安全的4项指标状态预测及相应的预测值，如表4所示，做综合安全指数拟合值曲线如图1所示。

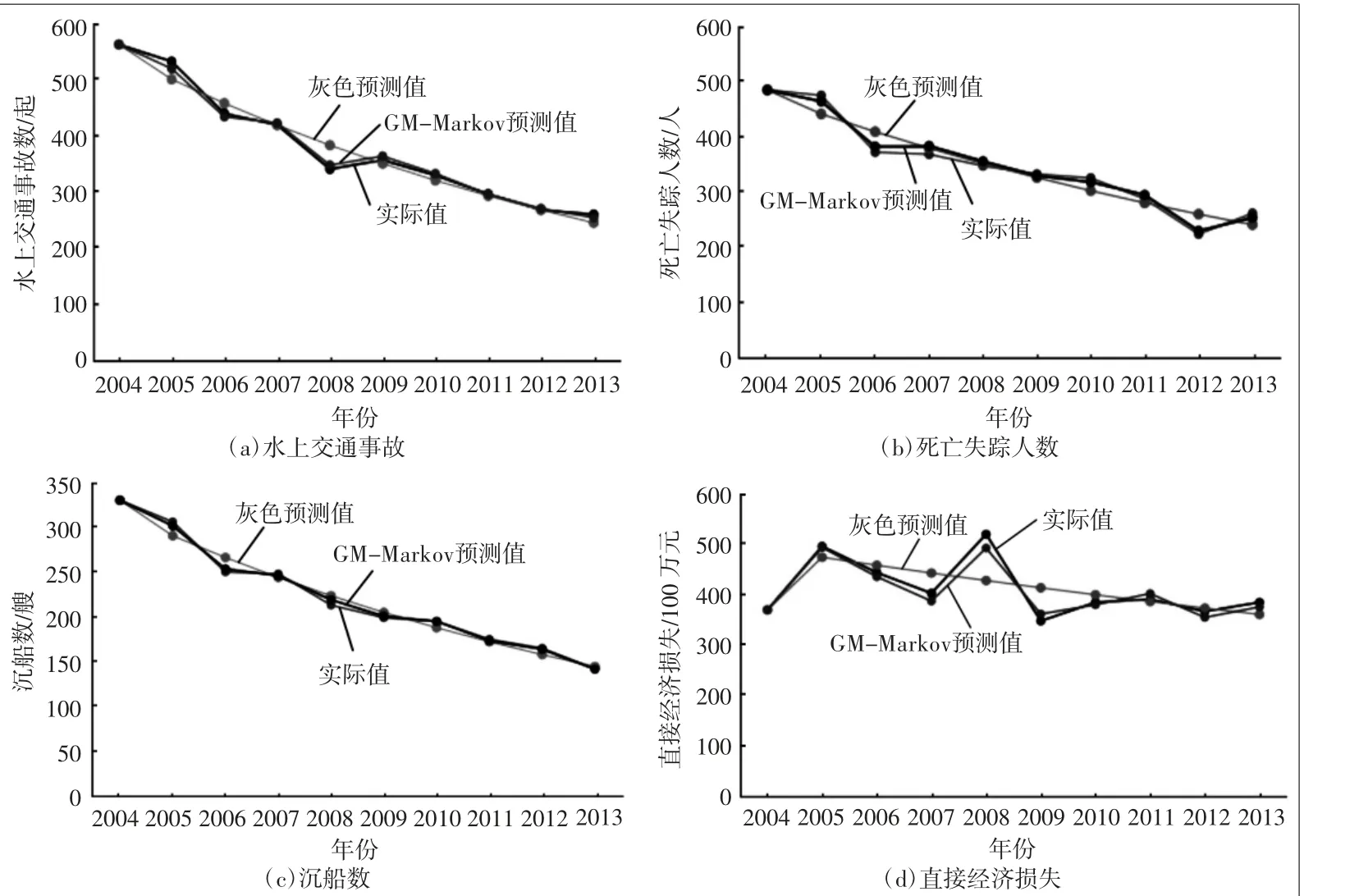
图1 2004—2013年4项指标灰色预测值和GM-Markov值的拟合曲线

可以看出，模型对波动性较大的指标存在较大的偏差。因此，采用GM-Markov模型对2014年的灰色预测值进行修正，得到修正后的马尔可夫预测，如表4所示。

表4 2014年水上交通事故数状态预测及预测值

根据计算，可得出2014年船舶水上交通安全4项指标的灰色预测值相对误差分别12.96%、8.30%、5.96%、34.32%，GM-Markov预测值的相对误差分别为9.69%、3.60%、2.41%、27.68%，相对误差均有不同程度的下降，由此可说明灰色马尔科夫预测模型相对于灰色预测模型具有较高的预测精度。

3 GM-Markov模型的预测精度与可行性分析

3.1 GM-Markov模型的预测精度分析

根据我国2003—2014年水上交通安全综合指数的实际值、灰色动态预测值和修正值，分别计算灰色预测值和修正值与实际值相对误差的均值、后验差比值和小概率误差，如表5所示。以水上交通事故数为例，结合模型精度划分表（如表1），灰色预测模型的均方差比C（C1=28.24%＞C2=7.42%）和相对误差Q （Q1=3.37%＜Q2=1.26%）均大于GM-Markov预测模型（C和P数值越小，模型精度越高，GM-马尔科夫模型的预测精度就越高[9]）。

表5 两种预测模型的精度分析

同理，可知灰色预测模型的相对误差均值为4.75%，而GM-Markov的仅为1.75%，下降了3%。结果表明：GMMarkov预测结果比单纯的灰色预测结果要精确很多，说明GM-Markov预测模型比灰色预测模型具有更高的可信度。

3.2 GM-Markov模型的可行性分析

为验证利用GM-Markov模型船舶水上交通安全综合指数各项预测的可行性，采用灰色预测模型和GMMarkov模型对2014—2019年的4项指标进行预测。

通过计算，分析2014—2019年的相对误差，如表6所示。结果表明：GM-Markov预测模型较传统灰色预测模型精度有了明显的提高[10]，且短期预测具有较好的拟合度，而中长期预测有较大的偏离度；GM-Markov预测模型对水上交通安全综合指数的短期预测效果较好，而对中长期的预测存在精度不高的现象，即表明GM-Markov预测模型在短期预测中具有一定的可信度。

表6 2014—2019年预测的相对误差均值比较

以2010—2019年4项指标原始数据为基础，运用GMMarkov预测模型进行预测，得到2020年和2021年的预测值，如表7所示。

表7 2020—2021年船舶水上交通安全的4项指数预测

从表7可以看出，4项指标2020年的预测值与2020年的数据相比有仍旧小幅度的回升，4项指标的变化与因为新冠疫情使得我国航运业空前繁荣的趋势一致；同时，新冠疫情肆虐全球，给船员的换班和遣返造成很大影响，导致大量船员在海上工作时间与协议不一致，船员疲劳、超期工作、遣返困难等将给船舶带来巨大的安全风险，希望相关部门能特别注意今年的船舶水上交通安全问题。

4 结论

1）该模型是在传统灰色模型的基础之上构建的，因此继承了灰色模型的优势，需要较少的历史数据，避免了其它方法中“大范围、长周期、低精度”的弊端，可以比较充分地利用有限的数据。

2）基于水上交通综合安全指数的特点，将灰色动态预测与马尔科夫预测相结合，建立了GM-Markov马尔可夫预测模型，研究表明这种方法对于4项指标的预测有较好的效果，提高了预测的精确度。

3）通过对比分析可知灰色预测模型只是反映了4项指标整体的发展趋势，对于具有随机性、突发性和偶然特点的问题偏差较大，而GM-Markov模型能够很好地修正此偏差，对船舶水上交通安全综合指数的拟合程度和未来走势较为准确。

4）受新冠疫情的影响，航运业受到了很大的冲击，国际贸易呈现低迷的态势，因此相关部门应充分认识4项指标的GM-Markov预测值，针对国内外的海域环境，对有关资源做出中长期的战略调整，从而确保航运业健康、安全和平稳地发展。

总之，GM-Markov模型可以作为船舶水上交通安全指数预测的数据模型，GM-Markov模型相对精准的预测能帮助水上交通安全主管机关制定更为完善的预防措施，在误差允许的范围内，为船舶水上交通安全4项指标的预测提供新的理论基础。