含运动副间隙的舵机用空间4R执行机构动态特性研究
2021-10-26张华宋梅利杜英杰
张华,宋梅利,杜英杰
(南京理工大学 机械工程学院,江苏 南京 210094)
0 引言
弹道修正技术以其低成本、高精度等优点,逐渐成为制导弹药技术研究的热门领域[1],其中以电动舵机操作鸭舵的修正技术来进行弹道二维修正,能够提供较强的修正能力,对提高弹药的打击精度有重要意义[2]。在实际舵机系统中,间隙的存在会使舵翼的偏转产生偏差,降低系统的运动精度;当舵机系统含间隙时,运动副之间会产生碰撞和冲击,恶化机构的动态特性[3]。
国内外研究人员对含间隙机构动力学问题进行了大量的分析和研究。DUBOWSKY S等[4]基于牛顿法的二状态模型,对含间隙机构的动力学特性进行了定量分析;FUNABASHI H等[5]基于牛顿法,对不同运动副存在间隙时进行了分类建模,并且通过与大量的实验结果进行对比,验证了所建模型的合理性。MIEDEMA B等[6]基于动量定理,将运动副间隙的状态分为3种,即接触、分离和碰撞。FURUHASHI T等[7]基于连续接触模型对存在多个转动副间隙的四杆机构建模,并使用拉格朗日方法建立了该机构的运动方程。目前针对含间隙的舵机用空间4R机构的研究较少且普遍未考虑因弹性体变形而引起的动态特性变化。对于多体系统,各个零件材料不尽相同,分析间隙和柔性体对机构动态特性的影响具有实际意义。
本文主要针对舵机用空间4R执行机构,利用L-N接触力模型和修正的Coulomb摩擦力模型,仿真分析不同间隙大小对机构动态特性的影响,探究机构间隙尺寸的最佳范围。建立机构的刚柔耦合模型,分析间隙作用下构件的弹性变形对空间4R执行机构动态特性的影响。
1 含间隙模型建立
本文以图1所示空间4R机构进行建模,其中构件0为机架,构件1为输入轴,构件2为连杆,构件3为输出轴,各个构件通过转动副连接。4个转动副的轴线相交于构件3的几何中心。

图1 空间4R机构简图
本文采用Lankarani和Nikravesh接触力模型(L-N接触力模型),该模型的接触力公式为[8]
(1)
式中:Kδn为碰撞过程中的弹性变形力,其中K是等效的刚度系数,δ是两碰撞物体法向侵入深度,n是碰撞力的指数,对于金属材料取1.5。K取决于接触面的材料和几何属性,当两个构件相接触时,K可由下式计算:
(2)
(3)
其中ν和E分别表示构件的泊松比和弹性模量。

D=μδn
(4)
其中μ为滞后阻尼因子。在L-N接触力模型中,由于机构内部阻尼的存在,会导致接触碰撞过程中能量的耗散。
根据能量守恒定律,在接触碰撞前后两物体的动能损失可表示为
(5)

对碰撞力进行积分同样可求得碰撞过程中物体的动能损失:
(6)
将式(5)和式(6)联立,可得
(7)
因此式(1)进一步可表示为
(8)
L-N接触力模型考虑了物体材料、变形、相对速度等因素的影响,能较为准确地表示碰撞过程中物体能量的损失情况,在含间隙机构动力学研究方面具有广泛的应用场景[9]。
当机构运动副存在间隙时,除需建立接触力模型外,还需考虑摩擦力的作用。本文采用修正的Coulomb摩擦力模型描述间隙摩擦力,其切向摩擦力Ft可以表示为
(9)
式中:μf为动摩擦因数;cd为动态修正系数;vt为切向相对速度。
2 含间隙机构多刚体动力学仿真分析
基于上述碰撞接触力模型和摩擦模型,利用ADAMS软件内置的IMPACT函数对机构进行仿真分析。依照图1所示的运动简图建立如图2所示的含间隙空间4R机构仿真模型,其中构件1为输入轴、构件2为连杆、构件3为输出轴。设计要求输出轴可以绕其轴线正负转动20°,误差<0.1°。间隙1位于输入轴1与连杆2间的转动副处,间隙2位于连杆2和输出轴3之间的转动副处,两转动副的基本尺寸均为16mm。设计加工精度为IT7级。

图2 含间隙空间4R机构示意图
为构件1添加一个旋转驱动,设置驱动转速为20r/s,其他仿真参数如表1所示。

表1 ADAMS中接触力参数
利用ADAMS分析含间隙的多刚体空间4R机构不同间隙大小和间隙数目的动态特性的影响,并探究舵机用空间4R机构存在间隙时的最佳间隙量。
2.1 间隙对机构动态特性的影响
仅考虑间隙1的作用,根据机构的尺寸和设计加工精度计算间隙的极限间隙[10],在极限间隙范围内取间隙尺寸分别为0.04mm、0.10mm和0.50mm,探究间隙对输出轴角位移和接触力的影响,仿真结果如图3所示。

图3 不同间隙时输出轴角位移变化的局部放大图
从图3可以看出,当机构不含间隙时,曲线光滑且无偏差;当间隙为0.04mm时,曲线光滑,最大误差为0.027 5°,满足设计要求;当间隙为0.10mm时,曲线变得不光滑,最大误差为0.088 7°,同样满足设计要求;当间隙为0.50mm时,曲线不光滑,最大误差为0.446 9°,不满足设计要求。可见,随着间隙尺寸的增大,机构的运动精度逐渐下降。
图4为不同间隙时输出轴与连杆之间的接触力图(本刊黑白印刷,相关疑问请咨询作者)。当间隙为0.04mm时,接触力的均值为195N;当间隙增加到0.10mm时,接触力的均值为321N;当间隙为0.50mm时,接触力的均值为4 527N。这是由于随着间隙增大,运动副元素之间的相对碰撞次数减少,相邻两次碰撞间隔增加,惯性力作用时间更久,碰撞前两构件相对速度更大,故接触力增大。

图4 不同间隙时输入轴与连杆之间的接触力图
由图4可知,随着间隙的减小,构成运动副的两物体碰撞次数增多,间隙接触力相应减小并趋向理想机构运动副反力。间隙越小,对机构动态特性的影响越小,机构的稳定性也越好。但由于间隙中存在摩擦,当间隙小到一定程度时,摩擦的影响反而导致间隙接触力增大。因此需要研究机构的最佳配合间隙量。
2.2 分析确定最佳配合间隙量范围
设输入轴与连杆之间的间隙大小分别为0.03mm、0.04mm、0.05mm、0.10mm和0.20mm,对其进行动力学仿真分析,研究接触力和输出轴角位移在不同间隙情况下的变化,仿真结果如图5所示。

图5 不同间隙时输入轴与连杆之间接触力对比图
由图5(a)可知,间隙为0.04mm时接触力曲线的波动相对于间隙为0.03mm时接触力曲线较小,且接触力的幅值较小,约为6 000N。由2.1小节的结论可知,由于间隙的碰撞模型中考虑了摩擦力,当间隙减小时,摩擦的影响增大,从而使机构间隙为0.03mm时的接触力大于间隙为0.04mm时的接触力。由图5(b)可知,间隙在0.04mm和0.05mm时接触力曲线变化不大,两个周期内接触力的大小几乎相同,此时摩擦力在碰撞过程中产生的影响不大。故可得出,此空间4R机构在间隙<0.04mm时,摩擦力对机构接触力的影响将增大。
由图6(a)可知,当间隙为0.10mm时输出轴角位移相对于不含间隙情况的最大误差为0.090 7°,满足设计要求。由图6(b)可知,间隙为0.20mm时输出轴角位移相对于不含间隙情况的最大误差为0.142 9°,不满足设计要求。结合此前分析结果可以得出结论,此空间4R机构实际工作时的合适间隙范围约为0.04mm~0.10mm。

图6 不同间隙时输出轴角位移时间历程图
2.3 含两间隙时机构的动态特性研究
同时考虑图2中间隙1和间隙2对舵机执行机构动态特性的影响,对含两间隙机构进行动力学仿真,仿真结果如图7所示。
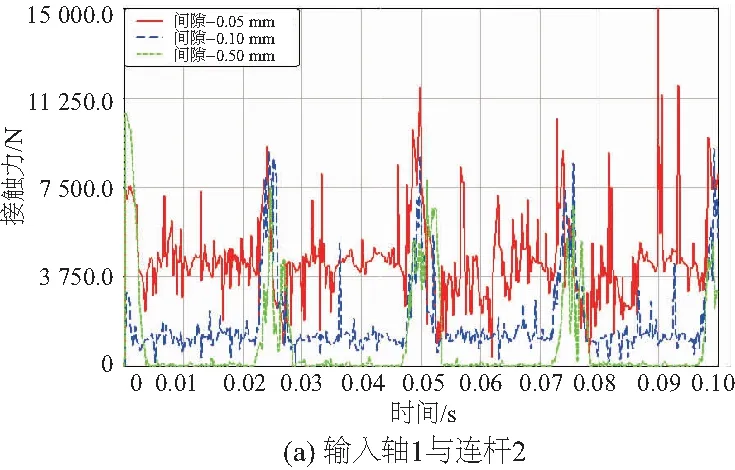
图7 含两间隙条件下输出轴接触力时间历程图
由图7可知,随着间隙的增大,两处间隙之间的碰撞均有所缓和,接触力都出现相对减小的趋势,幅值分别下降了39.3%和46.4%。其原因在于两间隙存在相互耦合的作用,两间隙之间的相互作用使得机构受力情况发生改变。间隙数量的增多,增加了机构整体的间隙碰撞次数,加快了构件动能的耗散,使单个间隙的接触力幅值减小。
为进一步探究含两间隙机构在实际工作时合适的间隙尺寸,取不同的间隙进行动力学仿真分析,输出轴角位移的仿真结果如图8所示。

图8 含两间隙不同间隙时输出轴角位移时间历程图
由图8可知,当间隙为0.07mm时输出轴角位移的最大误差为0.086 4°;间隙为0.06mm时输出轴角位移最大误差为0.092°;间隙为0.05mm时输出轴角位移的最大误差为0.290 4°。分析可知,随着间隙的减小,输出轴角位移的误差逐渐增加。其原因是间隙中存在摩擦,当间隙小到一定程度时,摩擦力的影响增大,影响输出轴的偏转,降低机构的运动精度。故可知,此舵机用空间4R机构间隙值的下限约为0.06mm。
当间隙为0.10mm时,输出轴角位移的极大值为20.070 4°,极小值为-20.064 9°,角位移的曲线光滑,满足精度要求;当间隙为0.20mm时,输出轴角位移的极大值为20.319 3°,极小值为-20.282 8°,角位移的曲线变得不光滑,且不满足精度要求。结合前面的分析结果可以得出,该舵机用空间4R机构实际工作时合适的间隙范围约为0.06mm~0.10mm。
3 含间隙机构刚柔耦合仿真与分析
对于多体系统,各个零件材料不尽相同,不同材料的变形特性也不同,对系统进行刚柔耦合分析结果更接近工程实际应用。本节对含间隙舵机用空间4R机构进行刚柔耦合仿真研究。
3.1 关键部件柔性体的建立
对舵机用空间4R执行机构的关键部件进行柔性体建模,以分析其在受载变形时对输出轴运动精度的影响;分析在间隙作用下柔性体的存在对机构动态特性的影响。本节以连杆2作为柔性体,在ANSYS软件中进行柔性体网格划分,然后导入ADAMS软件中,导入后的刚柔耦合仿真模型如图9所示。

图9 4R空间机构刚柔耦合模型
3.2 仿真与分析
取间隙为0.08mm,设置仿真时间为0.1s,仿真步数为100步,进行动力学仿真分析,输出轴角位移曲线在不同条件下的仿真结果如图10所示。图10中曲线1-曲线5分别代表了无间隙无柔性体、单间隙无柔性体、单间隙有柔性体、两间隙无柔性体和两间隙有柔性体条件下的输出角位移的时间历程。
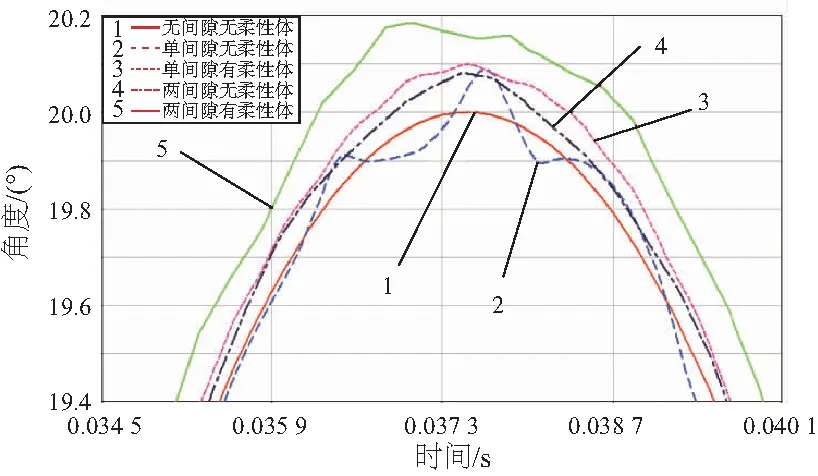
图10 不同条件下输出轴角位移时间历程的局部放大图
由图10可知,含间隙和柔性体对输出轴角位移的精度影响较大。通过和理想条件(多刚体无间隙)下输出轴角位移的对比,含间隙和含柔性体机构输出轴角位移的幅值均大于理想情况。由曲线2、曲线3和曲线4、曲线5对比可知,相较于刚柔耦合模型,多刚体模型的输出轴角位移曲线光滑且幅值更低,说明柔性体产生的弹性变形对机构输出轴角位移的不利影响较大。
输入轴与连杆的接触力仿真结果如图11所示。
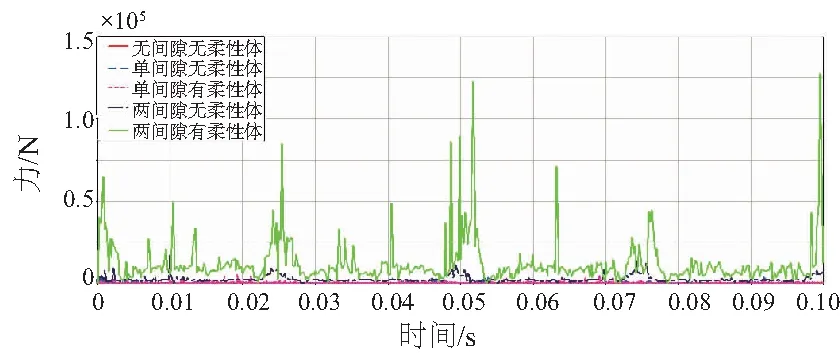
图11 输入轴与连杆间的接触力时间历程图
通过对比图中单间隙的刚性模型和刚柔耦合模型可知,在间隙大小和间隙数量相同的情况下,柔性体的存在使得机构间隙碰撞力峰值更大。当间隙数目增加到2时,柔性体的存在对机构间隙碰撞力的影响更强,间隙碰撞力峰值约为无柔性体情况下的7倍。故在实际生产加工的过程中,应尽可能保证零件的刚度要求。
4 结语
本文以舵机用空间4R机构作为研究对象,考虑运动副间隙的影响,通过仿真分析,探究了间隙大小对机构运动精度和运动副受力的影响,确定了当机构考虑单间隙和双间隙时的最佳间隙量范围。通过建立空间4R机构的刚柔耦合模型,分析了柔性体在受载变形时对输出轴运动精度的影响和在间隙作用下柔性体的存在对机构动态特性的影响。得到了以下结论:
1)间隙越大,机构的运动误差越大,对机构的破坏和磨损越剧烈;当两间隙同时作用,间隙之间运动副间的碰撞随间隙增大有所缓和。考虑单间隙时,该机构最佳间隙范围约为0.04mm~0.10mm;考虑两个间隙时,间隙量约在0.06mm~0.10mm范围内可以降低运动副间隙对机构的不良影响。
2)多刚体模型的输出轴角位移曲线优于刚柔耦合模型的输出轴角位移曲线,说明柔性体产生的弹性变形对机构输出轴角位移的影响较大;刚柔耦合模型的接触力幅值比多刚体模型的接触力幅值更大,说明了柔性体的存在会明显增强间隙碰撞带来的不良影响,并且柔性体对机构的影响随间隙数量的增多而增强。
