风电齿轮箱行星架多圆弧结构的优化设计研究

覃立，陈荣梅，郭勤涛

(1. 南京航空航天大学 机电学院，江苏 南京 210016；2. 南京安维士传动技术股份有限公司，江苏 南京 210019)

0 引言

在大型风电传动系统中，行星架承担着主轴传递过来的转矩，是风电齿轮箱中承载最大的零部件，在工程应用中前臂和前轴联接处时常会发生断裂、疲劳等故障[1]。行星架作为齿轮箱中最重要的零部件之一，为了保证风力发电机20年的运行寿命，须保证行星架具有足够的极限强度和疲劳强度[2]，因此行星架的强度设计研究具有重要意义。

在某些双臂行星架中，在前臂和前轴联接处设置有阶梯轴结构，如图1所示，以便于对支承行星架的滚动轴承轴向定位。显然，在阶梯轴的1、2两处存在应力集中现象。在机械零部件中，通常采用过渡圆弧来改善该现象，常见过渡圆弧构型有单圆弧、双圆弧和三圆弧等[3-4]。鉴于采用单圆弧过渡影响轴承装配且应力降低效果不明显。过渡多圆弧被作为一种低应力设计方案，但如何实现多圆弧参数优化设计并提高优化设计效率成为一个研究问题。

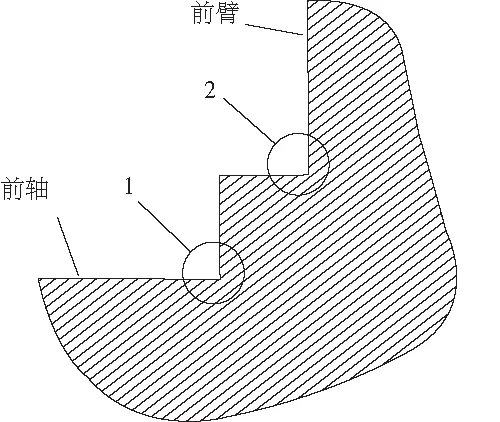
图1 阶梯轴结构

本文以两种圆弧构型即图1中1处采用双圆弧、2处采用三圆弧为例进行多圆弧结构优化设计研究。首先对多圆弧参数设计方法进行了研究，利用有限元和编程软件实现行星架多圆弧结构的参数化建模，最后进行了优化方法的探讨。

1 多圆弧曲线的参数设计

为了准确描述多圆弧曲线的形状和位置并保证设计参数之间相互独立，以三圆弧曲线为例，推导其通用的几何关系[5-8]，提取出设计参数。然后，利用该方法确定多圆弧结构的设计参数，为其优化设计提供理论依据。

1.1 三圆弧曲线的参数设计

图2 三圆弧参数的示意图

根据几何关系，可以推出圆心O1(xO1,yO1)、O2(xO2,yO2)、O3(xO3,yO3)的坐标：

(1)

(2)

(3)

根据三圆弧的相切条件，可得

(4)

在图2中，线段ED为与多圆弧相接的已知结构，以D点为原点，ED为x轴，建立坐标系x1Dy1，α为两坐标系y轴相交形成的锐角。在三圆弧形状确定时，α可以控制三圆弧结构的位置，需将其作为独立变量，用公式(5)可将圆弧上点的坐标从坐标系x2Oy2转换到坐标系x1Dy1上，即将坐标(x2,y2)转换成坐标(x1,y1)。

(5)

因此，为了确定三圆弧曲线的位置和形状，共需采用6个独立变量。应用该参数设计方法，单圆弧和双圆弧的独立变量数目分别为3个和4个。此外，圆弧段数>3的多圆弧曲线也可利用上述方法确定独立变量。

1.2 多圆弧结构的参数设计

多圆弧结构的母线如图3所示，结合上一节的参数设计方法和实际位置约束(点A、D、F、H均固定不动)，该母线可用8个独立参数描述，其中三圆弧段5个，两圆弧段3个，其参数范围如表1所示。

图3 多圆弧结构的示意图

表1 多圆弧结构的设计参数及范围

2 行星架的应力分析

2.1 参数化建模及应力分析过程

图4为联合MATLAB和HyperWorks两种软件对多圆弧结构参数化建模的方法：利用MATLAB编程，用设计变量控制多圆弧曲线的形状和位置，并调用MESH2D工具箱[9]生成多圆弧结构截面的二维网格模型，在HyperMesh中建立多圆弧结构和整体行星架的三维网格模型，此外还需利用MATLAB程序和HyperWorks的二次开发功能[10]保证参数化建模过程的可重复性。

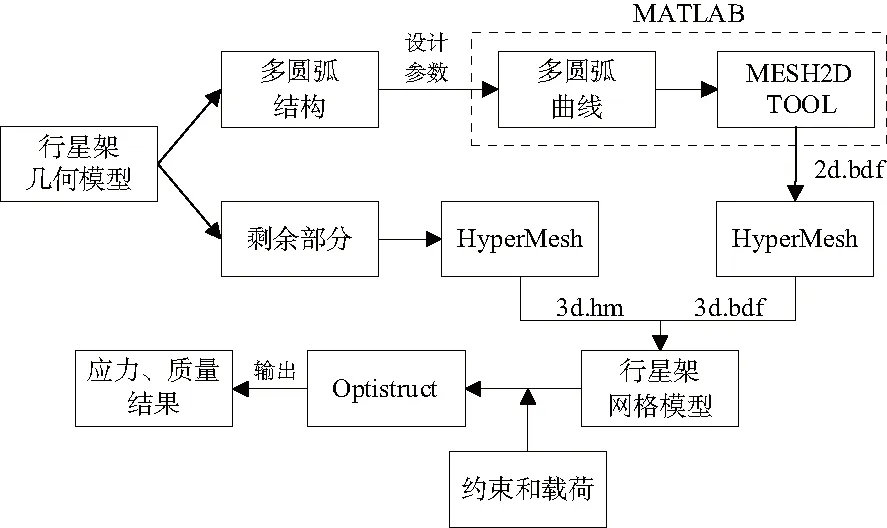
图4 行星架参数化建模及应力计算过程

图5为行星架的有限元模型及边界条件。许多学者对行星架的极限强度分析做了大量的工作[11-12]，本文不再赘述该过程。行星架的材料为QT700-2A，其疲劳极限为380MPa，材料局部安全系数为1.1，其他安全系数均考虑在载荷中，此时疲劳强度许用应力[σ]为345MPa。同时，分析应力类型为最大主应力[13]，且需用许用应力评判结构是否满足强度要求。

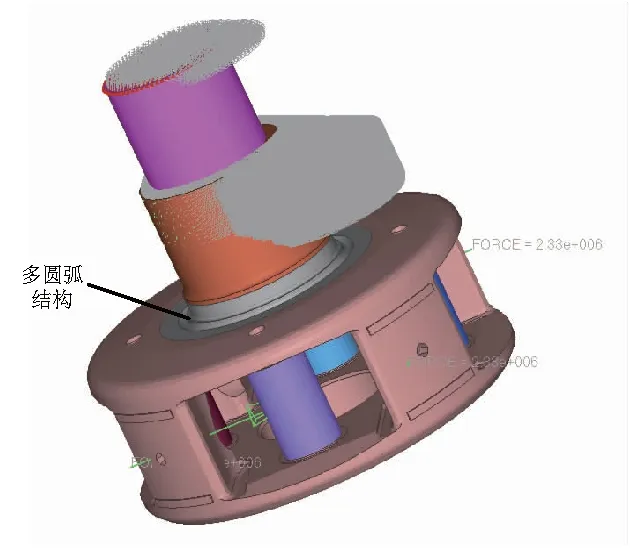
图5 行星架的有限元模型及边界条件

2.2 多圆弧参数与应力、质量的变化关系

基于表1中的设计参数和图4的应力分析过程，可以开展多圆弧参数与多圆弧结构上最大应力、质量之间的变化关系研究。

三圆弧的形状和位置由5个独立设计参数R1、R2、R3、α1和β1确定，固定两圆弧的设计参数，此时可取R5=18mm，α2=80°，β2=18°。在设计参数的取值范围内取等距的7个值，探究σl,max、σs,max和质量随单一参数的变化规律，如图6-图8所示。

图6 两圆弧处最大应力与参数的变化关系

图7 三圆弧处最大应力与参数的变化关系

图8 参数化部分质量与参数的变化关系

从图6-图8中可以看出，两圆弧处的应力值明显高于三圆弧处，并可能超过许用应力值；质量和σl,max应力随着参数R2、β1的增大而增大，随着参数R1、R3、α1的增大而减小，σs,max的变化规律与之相反；5个参数对两个圆弧段上的应力均有影响。其中，σl,max表示两圆弧段上最大应力，σs,max表示三圆弧段上最大应力。另外，两圆弧的参数也符合类似规律。

3 多圆弧结构的优化设计

3.1 优化问题的建立

基于2.2节中多圆弧参数与质量的变化规律可知，当R1=35mm，R2=15mm，R3=8mm，α1=65°，β1=7°，R5=14mm，α2=60°和β2=40°时，质量取最小值0.231 8 t，此时应力σl,max=375.3MPa，σs,max=261.7MPa。σl,max超出了许用应力，因此不满足疲劳强度要求。为了对多圆弧结构进行低应力和低质量设计，本文以多圆弧结构的8个参数作为设计变量，应力满足疲劳强度要求作为约束条件和参数化部分质量最小作为目标函数建立优化问题，数学模型如下所示。

3.2 多种代理模型的实现

行星架有限元模型每进行一次静力学分析需耗费时间为5 min左右。由于涉及8个设计变量，在优化过程中可能会迭代计算成千上万次，若基于有限元模型反复计算响应，必将产生巨大的时间成本。为了减少仿真计算时间，可采用代理模型技术[14]，它可以代替实际物理模型的计算过程。

在建立代理模型时，试验设计方法和近似模型直接影响代理模型的精度[15]，可对比不同试验设计和近似模型下代理模型的精度选出最优方案。采用正交设计、拉丁超立方和优化超立方三种试验设计方法获取模型样本点，样本点数如表2所示，并利用该样本点分别构建多项式响应面模型、Kriging模型和径向基模型，然后使用测试点验证方法[15]对模型精度进行检验，其中验证样本点为同一组拉丁超立方抽样的样本点。图9为σl,max应力代理模型精度对比图。在模型样本点数相当的情况下，正交试验设计的代理模型精度明显优于其他两种设计方法，所以试验设计方法选用正交设计。在正交设计下，σl,max应力的三阶多项式响应面模型精度最高，σs,max应力的径向基模型精度最高，质量的径向基模型精度最高，依此可以确定各目标量最优的近似模型。各目标量代理模型的优选方案如表3所示。

表2 试验和验证的样本点数

图9 σl,max应力代理模型的精度对比

表3 各目标量代理模型的优选方案及精度

3.3 基于粒子群算法的结构优化

在建立高精度的代理模型后，可采用优化算法求解优化模型的最优解。粒子群算法在求解优化问题时表现出良好的寻优能力，通过迭代寻优计算能够迅速找到最优解，因此粒子群算法在工程计算中广泛应用[16]。本文将质量最小时的参数作为优化初始值，采用粒子群算法对优化问题进行求解。

优化前后的结果比较如表4所示。从表中可以看出，优化后两圆弧段的应力值为338.5MPa，比优化前降低了9.8%，三圆弧段应力变化不大，均满足疲劳强度条件，同时多圆弧结构质量降低了5.7%。

表4 优化前后的变量值及变化量

4 结语

本文提出了基于代理模型和粒子群算法的多圆弧结构优化设计方法，并将其应用在风电齿轮箱中行星架上，具体的研究内容及后续研究任务如下：

1)推导了双圆弧和三圆弧通用的几何关系，为多圆弧结构的参数设计提供了理论依据，并基于MATLAB和HyperWorks联合建模方法建立了多圆弧结构的参数化模型；

2)结合粒子群算法和代理模型进行多圆弧结构的优化设计，降低了多圆弧结构上应力的最大值，并显著提高了优化效率；

3)由于时间和经济等原因，尚未制造出优化后的物理模型以对该套方法进行验证，之后可进一步研究试验验证的工作。