基于逐步判别分析的颜色读数与物质质量浓度预测的研究

李兴莉 蔡红梅

1 重庆建筑科技职业学院（重庆 401331）2 电子科技大学成都学院（四川成都 611731）

比色法是目前常用的一种检测物质质量浓度的方法，常用的方法有2种：目视比色法和光电比色法。目视比色法是将试样溶液滴在特定的试纸表面，等其充分反应以后生成一张颜色稳定的试纸，再将该颜色试纸与标准比色卡进行比较，目视找出色泽最相近的色阶，从而确定待测物质的质量浓度档位。每个人对颜色的敏感差异使得结果有偏差。虽然光电比色法消除了主观误差，但也有其缺点（只适用于可见光谱区及只能得到一定波长范围的复合光），以致比色法后来逐渐被分光光度法所代替。

比色法的主要优点是设备简单和操作简便，如果能准确判断颜色试纸与标准比色卡哪一类色阶相同，则能提高比色法的准确性。随着照相技术和颜色分辨率的提高，照片颜色读数可靠性不断提高，为比色法的改进提供了新的思路。本研究通过分析颜色读数和物质质量浓度的关系建立模型，由颜色读数通过模型准确判断待测物质的质量浓度。采用逐步判别法建立二氧化硫溶液（二氧化硫与水制成的溶液）颜色读数［B（Blue）=蓝色颜色值、G（Green）=绿色颜色值、R（Red）=红色颜色值、H（Hue）=色调、S（Saturation）=饱和度］与质量浓度（mg/L）的关系模型，由判别函数能准确判断二氧化硫质量浓度。

1 逐步判别分析方法

判别分析建立的判别函数受变量的影响，变量过多会增加计算量，同时一些不重要的变量可能会干扰判别函数的建立，使得判别函数不能准确判别。另外，如果将一些重要的变量删除，建立的判别函数也不能进行有效判别。逐步判别法可以解决变量选取问题，从而使得判别更加准确。逐步判别法采用有进有出的方法动态选取变量。

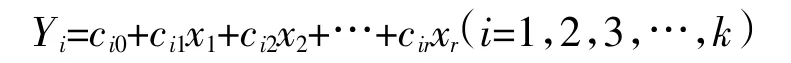
需要判断一个样品的质量浓度时，只需要将变量x1，x2，…，xr的数据代入判别函数，计算出每个判别函数值Y1，Y2，Y3，…，Yk，样品质量浓度是最大函数值对应的数值。

2 逐步判别分析建立二氧化硫颜色读数与质量浓度关系模型

将31 组训练数据，包含5 个变量（B，G，R，H，S）的二氧化硫颜色读数，以及分类变量二氧化硫质量浓度（0，20，30，50，80，100 和150 mg/L）导入SPSS软件中，按照步骤分析（Analyze）→分类（Classify）→判别（Discriminate）选择逐步进入方式，可以得到分类结果。

2.1 逐步进入步骤分析

将F进设为5，F出设为3.5，得到变量逐步引入的各项数据、指标（见表1），以及引入变量是否显著，是否剔除的各项数据、指标（见表2）。

从表1 数据可以知道每次是否有变量被选入。第一次最大F值为5 323.871，对应变量G，且对应Wilks 的Lambda 值最小为0.001，所以变量G 首先被引入模型；第二次判断变量H 的F值为56.120，是还未被引入变量中最大的，且Wilks 的Lambda 值小于0.001，所以变量H 第二个被引入模型；第三次判断后被选入的是变量B；第四次判断后被选入的变量是R；第五次判断变量S 的F值小于F进=5，因此变量S 不被引入模型。

从表2 可知，每次变量被选入之后，判断是否将其剔除时，计算出的F值都大于F出=3.5，所以这4个变量都不被剔除。最终得到的判别函数中包含R，G，B，H4 个变量，对应判别函数中的x1，x2，x3，x4。

2.2 判别函数

由上述步骤分析得到Fisher 的线性判别式函数见表3。

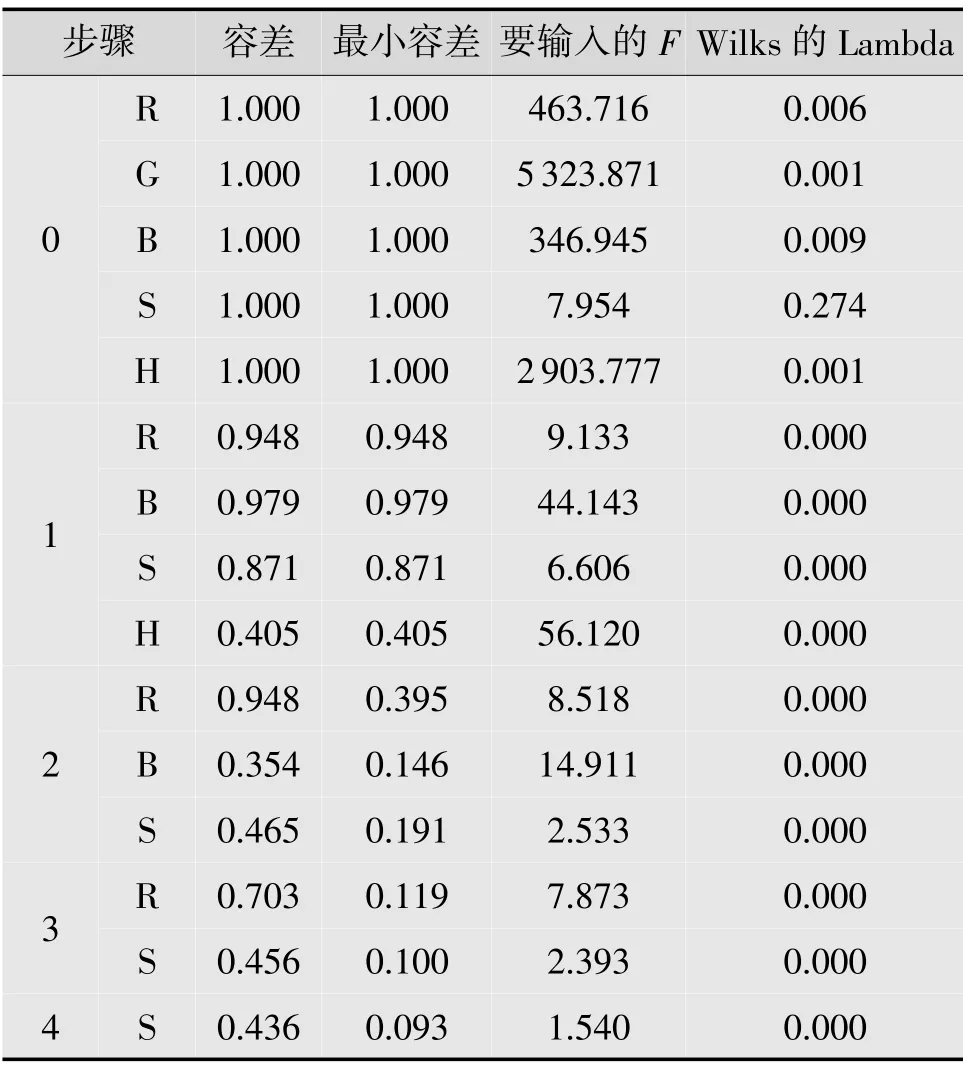
表1 不在分析中的变量

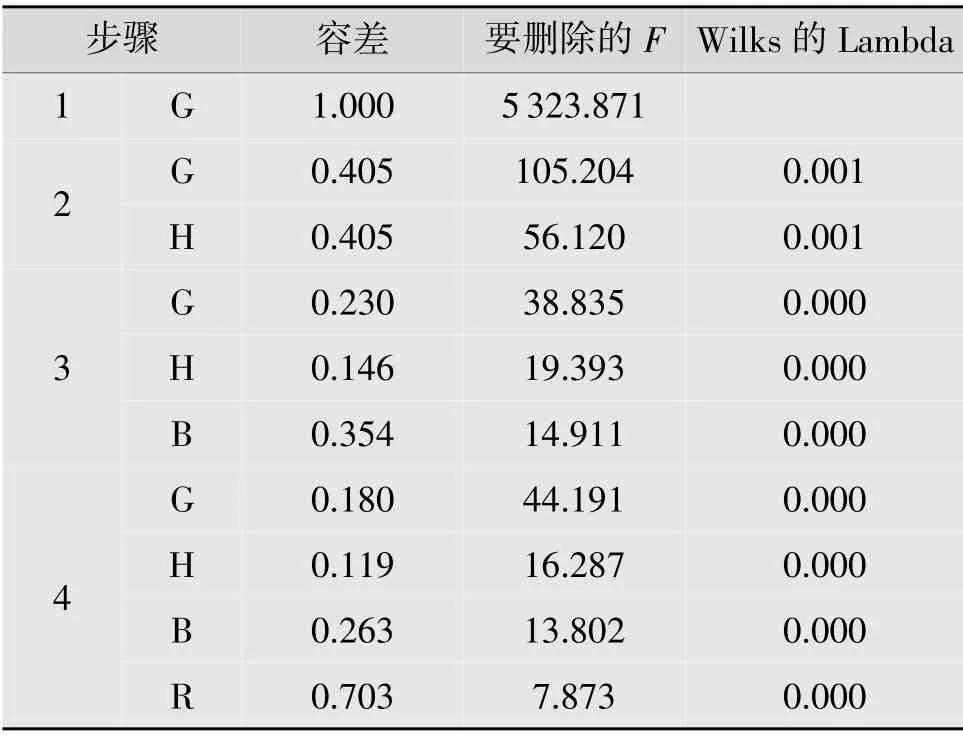
表2 分析中的变量

从分类函数系数可以得到判别函数：

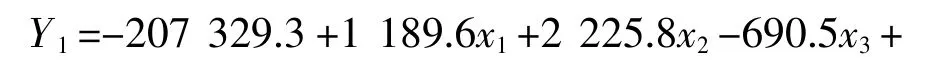
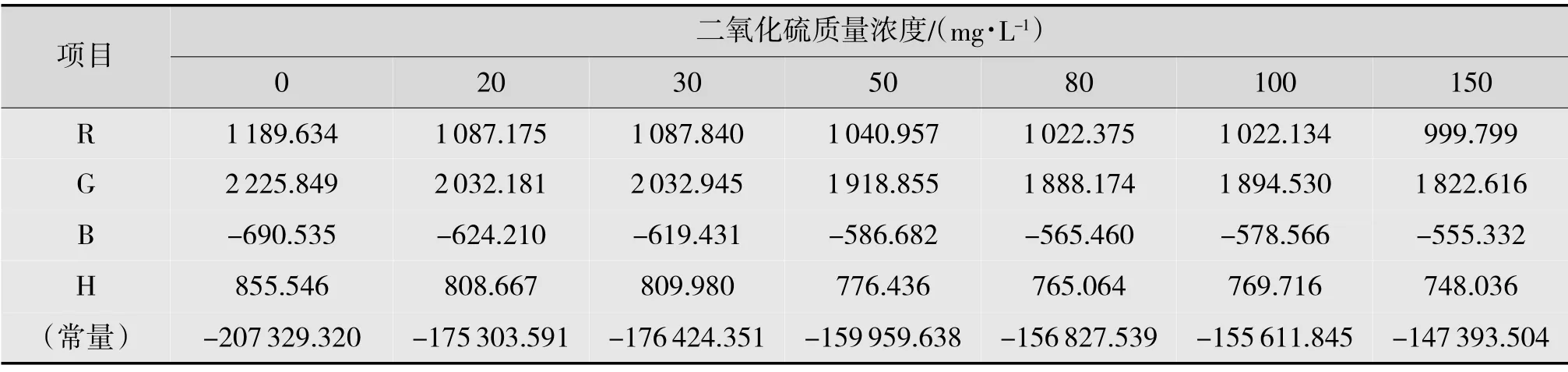
表3 分类函数系数

3 模型检验

对一个待测数据进行分类，只需要将数据中的R，G，B，H 分别代入7 个判别函数计算函数值，例如将测试组中的第一条记录代入判别函数，计算得F1=207 666，F2=205 126，F3=202 068.3，F4=202 058，F5=200 965.9，F6=201 091.1，F7=198 610，这些值中F1最大，所以属于第1 类，即质量浓度为0，与原始分类相同。利用该模型建立的判别函数对测试组的25组数据进行计算，得到的预测结果与原始数据完全吻合。

为了更好地说明该模型对二氧化硫质量浓度测定的准确性，作进一步分析。从前面二氧化硫的质量浓度判别分析模型知道：变量S 没有被引入判别函数，即如果减少变量S 再进行判别分析，得到的判别函数及结果不会发生变化。去掉变量S 用SPSS 软件进行分析，发现得到的结果与未去掉变量S 的分析结果一致。再将逐步进入法中最后进入模型的变量R，以及贡献一般的变量B 去掉后分析（即去掉S，R，B），发现虽然组质心、判别函数都不同，但是不影响模型的判别结果。以上3种不同维度判别分析得到的预测分类结果的准确率都是100%。减掉对模型贡献较大的变量G，H，B 之后进行判别分析，发现测试结果发生了变化，有部分误判。表4 显示了部分数据，其中Dis_1 是5 个变量R，G，B，S，H 作为自变量的预测结果；Dis_2 是去掉未被引入的变量S 后进行判别分析的预测结果；Dis_3 是去掉未进入模型的变量S 以及后进入模型的变量R、变量B 后进行判别分析的预测结果；Dis_4 是减掉对模型贡献较大的变量G，H，B 之后进行判别分析的预测结果。

从表4 可看出减掉对模型贡献较大的变量G，H，B 之后，判别分析得到的第8 条和第22 条记录结果与原结果不同。第8 条记录将质量浓度为20 mg/L 判断成了30 mg/L，而第22 条记录将质量浓度为150 mg/L 判断成了100 mg/L，结果判断有偏大也有偏小的情况。因此，随意减少变量对判断结果会有影响。表4 也说明逐步判别分析法在该模型中对变量的筛选非常准确，模型效果非常好。

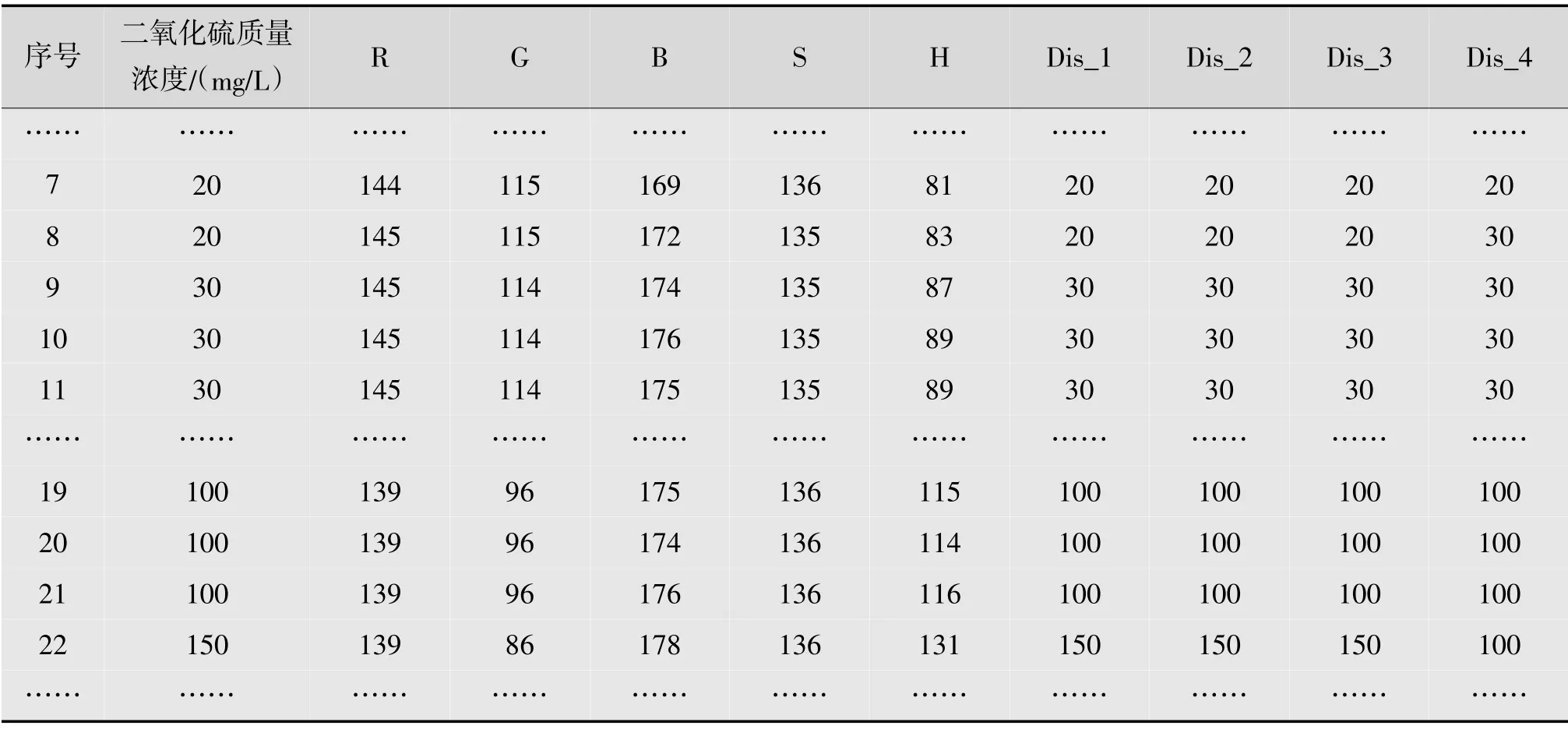
表4 几种不同变量的预判结果图

4 结论

用逐步判别分析法建立的二氧化硫颜色读数和其质量浓度的关系模型，能有效判断溶液的质量浓度，且精确度较高。该方法在化学物质检测中具有一定的参考价值，可以推广用于其他溶液（如溴酸钾溶液）质量浓度的测定，通过建立各自的判别函数，可提高比色法检测的准确度。