基于激励机制的家庭能量系统优化策略研究

刘 伟, 王 俊, 龚成生, 王 飞

(1. 东北石油大学 电气信息工程学院, 黑龙江 大庆 163318； 2. 国网山东省电力公司 曹县供电公司, 山东 曹县 274400)

0 引 言

如今光伏发电兴起和电动汽车的出现, 对智能电网需求侧管理问题的实现越来越急迫, 因此家庭能量的优化控制问题也需要不断向这个方向进行转变[1-2]。而家庭能量管理技术是体现在用户侧, 可以规划出家用负荷的分类以及分布式电源的优化控制, 为可再生能源接入需求侧提供支持[3-4]。目前, 国内外开展了很多关于家庭负荷调度问题的研究[5-7]。李中伟等[8]着眼于用电经济性以及用户舒适度的研究, 但对电网用电功率峰谷差的问题考虑不足。张延宇等[9]在智能电网环境下考虑了电动汽车在高电价时段的充放电特性对家庭能源管理系统的负载进行优化调度。佟晶晶等[10]和姚刚等[11]考虑电动汽车参与下对用电成本的影响, 但未考虑电动汽车入网对用电功率峰谷差调节的影响。李菁等[12]设计分时电价、 户用分布式光伏电源和储能装置, 建立基于经济性和舒适度的多目标优化模型。张军等[13]仅从电源侧考虑家庭用电功率的波动, 未考虑用户侧用电需求对电网功率波动的影响。综合以上分析, 笔者首先将家用电器进行分类建模以及充分考虑电动汽车充放电类建模, 电动汽车充放电标函数采用小生境的混沌粒子群优化算法进行仿真分析, 验证该调峰激励机制的有效性。

1 基本框架及其模型

1.1 家庭负荷

家庭居民用电分类负荷主要分为柔性负荷与刚性负荷[14]。其中柔性负荷的运行时间可以调控, 而刚性负荷的运行时间不可调控。其中柔性负荷可以分为两种： 1) 不可中断负荷； 2) 可中断负荷。其中不可中断负荷在运行期间不能改变其运行状态, 而可中断负荷在在运行期间可改变其运行状态。

不可中断负荷模型为

(1)

可中断负荷模型为

(2)

1.2 储能设备

蓄电池在家庭能量管理系统中起着至关重要的作用, 并于光伏发电系统配合参与用户侧电能的调控。其模型如下

(3)

其中SSOC为储能设备的荷电状态；Cbat为储能设备的额定容量；Pch、Pdisch为储能设备的充电功率与放电功率；ηch为其充电效率；Pdisch为蓄电池的放电功率,ηdisch为蓄电池放电效率；SSOCmin、SSOCmax为蓄电池最小、 最大荷电状态；Pch,max和Pdisch,max分别为蓄电池最大充电、 最大放电功率。

电动汽车与储能设备模型大体相同, 但存在如下3点区别[11]： 1) 电动汽车首先应满足出行要求, 故应考虑其接入时间的约束； 2) 由于蓄电池充放电会影响其寿命, 应考虑尽可能减少其充放电次数； 3) 为保证电动汽车的出行需求, 应保证其在离开时刻蓄电池荷电量满足最低出行标准。因此在蓄电池模型的基础上, 电动汽车需增加3个约束条件如下

(4)

其中αE、βE分别为EV运行区间的起止时刻；SSOCE为电动汽车荷电状态；PE为电动汽车充电功率；SSOCH为EV离开时刻最小SSOC限值。

1.3 温控负荷

温控负荷(如空调)是根据温度的改变确定其运行时刻以及运行功率的负荷。不同于柔性负荷其舒适度指标为负荷的运行时区, 而空调舒适度指标为室内温度, 其模型如下

(5)

其中Ti为室内设定温度；TL、TM分别为室内允许最低温度和最高温度；Tin为室内温度；Tout为室外温度；P为空调功率；α为室外温度对室内温度的影响系数；β为空调的运行系数,β<0为空调工作在制冷状态,β>0为空调工作在制热状态。

2 用户调峰贡献度的调峰激励机制及多目标能量调度优化模型

2.1 用户调峰贡献度的调峰激励机制

仅在固定分时电价策略的基础上进行用电优化很有可能造成大量的用电负荷集中到谷时电价区间运行, 构成新的用电高峰, 且可能不在系统负荷的供电谷时段, 这种错位新高峰会造成电力系统发电设备过负荷运行, 降低线路传输效率, 故仅依靠固定分时电价并不能达到预期效果。因此笔者从负荷侧参与电网调峰影响出发, 提出了对电网峰谷差有贡献度的激励机制, 达到削峰填谷的效果。

(6)

Cr=αmot(1-h(t))

(7)

其中h(t)为用户的调峰效果系数, 值越小说明用户用电负荷变动越不明显, 则调峰效果越显著；Pe(t)为第t个时刻用户的净负荷；αmot为电网公司的激励费率；Cr为激励成本, 用户参与电网调峰极极性越高, 用电负荷波动越小, 其激励收入越高。

2.2 目标函数

1) 经济性目标。以家庭用电成本最优为经济性目标, 其值越小, 说明经济性优化目标越好。

minF=Ct-Cr

(8)

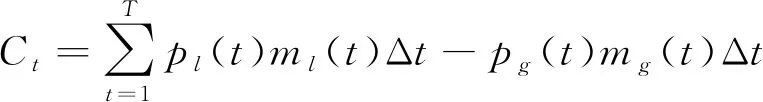
(9)

其中F为总用电成本；Ct为买电成本；pl为电网购电功率；ml为向电网购电价格；pg为卖给电网功率；mg为卖电价格。

2) 舒适性目标。以居民对负荷的用电行为习惯以及室内温度最佳为舒适度目标, 其值越大, 说明用户用电舒适度越好。

(10)

其中tsi为电器实际启动时间；Tsi为希望启动时间； ΔTi为允许工作时区长度,X为电器的总数。

3 算例分析

3.1 参数设置

算例系统中, 蓄电池和电动汽车额定容量均为5 kWh, 充放电效率均为0.8, 最大充放电功率分别为2 kW、1.8 kW, 蓄电池最小和最大荷电状态分别为0.2和0.9, 电动汽车最大和最小荷电状态为0.9和0.4, 蓄电池开始荷电状态为0.5, 由于出行需要, 电动汽车入网时间为0:00～7:00、 19:00～24:00。卖电价格0.42元/kWh, Δt=0.5,αmot=0.05。室内最低及最高允许温度分别为23 ℃和26 ℃。预测得到的光伏在每时段出力如图1所示, 不可调度负荷每时段出力如图2所示, 每时段电价信息如表1所示, 可调度负荷参数如表2所示。

图1 分布式电源功率 图2 不可调度负荷功率 Fig.1 Distributed power Fig.2 Undispatchable loads

表1 分时电价数据

表2 可调度负荷参数

3.2 结果分析

根据以上约束条件以及优化目标函数, 采用改进粒子群算法进行仿真分析, 结果如图3所示。

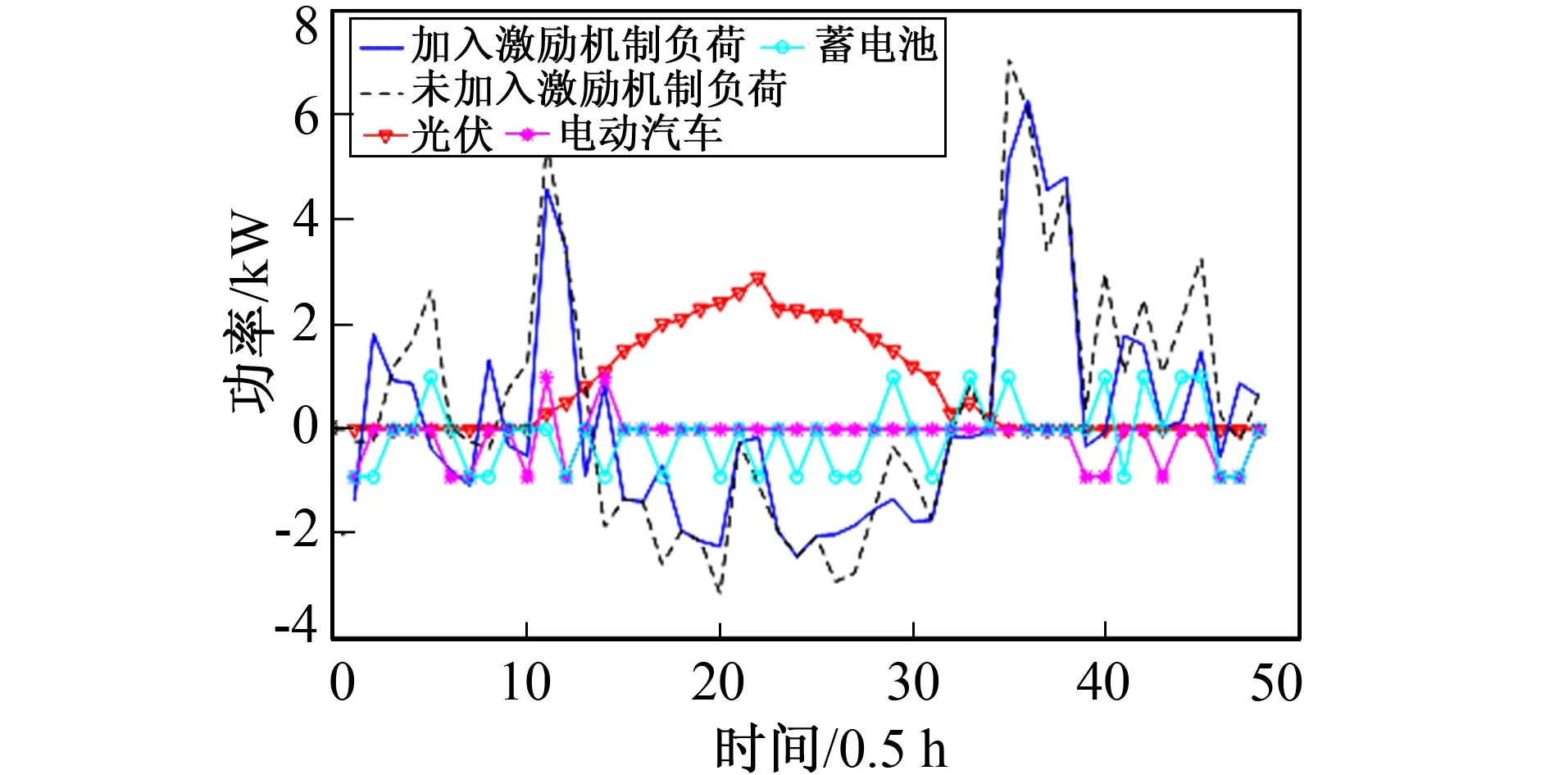
图3 负荷功率仿真图Fig.3 Load power simulation diagram

由图3分析可知, 在用电谷低谷且电价处于平时或谷时段, 加入激励机制对负荷峰谷差的影响不明显, 但在负荷处于峰值且电价处于峰时电价时段时, 提出的对电网调峰贡献度的调峰激励机制可以起到很好的削峰填谷作用, 在6:00～7:00、11:00～12:00和18:00～22:00家庭用电负荷功率处于高峰期, 激励机制有效地降低了负荷峰谷差, 加入激励机制后峰谷差降低12.5%, 从而降低了电网供电压力, 有利于电力系统的稳定。为验证所提出激励机制在减少负荷峰谷差以及用电成本的有效性, 表3列出了不同场景下的仿真结果。

表3 4种场景下特性对比

图4 适应度函数变化曲线Fig.4 Fitness function change curve

场景1为电动汽车只充电且未加入激励机制的情况, 此时电动汽车不参与负荷侧调峰, 负荷侧用电峰谷差以及用电成本较大。场景2为电动汽车充放电但未加入激励机制的情况, 对比传统电动汽车充电行为, 电动汽车充放电加入到负荷调峰后, 其优先充放电可以在用户用电高峰期充当蓄电池的作用, 很大程度上减少用电成本, 并对用户用电负荷峰谷差也有很大改善, 与场景1相比, 电动汽车考虑充放电特性后家庭用电成本降低2.2%, 负荷峰谷差降低1.7%。场景3为考虑电动汽车充放电特性并加入激励机制传统粒子群优化的情况, 可得到加入激励机制能有效减小负荷用电峰谷差和用电成本, 与场景2相比, 峰谷差降低12.1%, 用电成本减少7.2%。场景4为考虑电动汽车充放电特性并加入激励机制的基于小生境的混沌粒子群算法优化情形, 结果表明该改进算法比传统粒子群在降低负荷峰谷差以及家庭用电成本方面更有优势, 与场景3相比, 峰谷差降低3.7%, 用电成本减少2.9%。

表4 不同控制策略下的数据对比

从图4中可以看出, 基于小生境的混沌粒子群算法与传统粒子群相比, 收敛精度优于传统粒子群, 并克服了传统粒子群容易陷入早熟的缺陷。

由表4可知, 从用户舒适度的角度比较, 笔者的策略不及文献[14]中的策略理想, 但从成本下降率比较, 笔者所提的策略比文献[14]中的策略成本降低幅度更大, 因此笔者提出的激励机制能有效降低用户的用电成本。

4 结 语

笔者从用户负荷参与电网调峰的角度出发, 在建立家庭负荷用电模型的基础上, 提出了用户侧调峰激励机制, 并采用基于小生境的混沌粒子群算法进行优化。仿真分析表明, 提出的调峰激励机制能兼顾电网和用户侧的利益, 减少用户用电成本以及降低系统峰谷差, 在不影响用户需求的基础上, 节约了电力系统供电设备的使用容量以及降低线路和变压器的线路损耗, 很大程度上减轻了电网压力, 从而提高系统运行稳定性。