在数与形之间感悟数学思想

裘一能 裘迪波

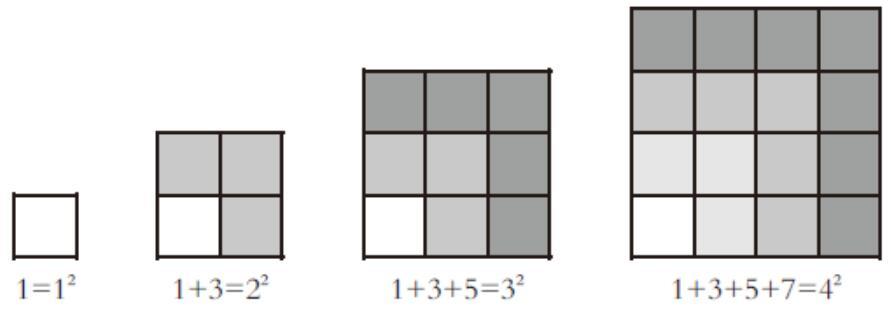
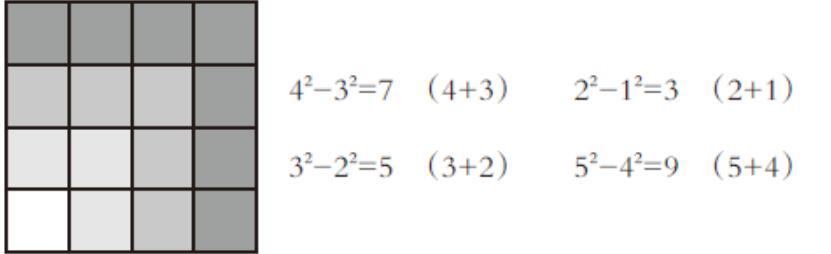
【摘要】本文以特级教师叶柱《数与形》教学片段赏析为例，论述引导学生在数与形之间感悟数学思想的策略，将数的问题转化成形的问题，从直观的图形表征中寻找计算方法;通过数与形之间的相互转换，让学生体会到数与形都是表征问题的方式，由此打通形象思维与抽象思维之间的通道。

【关键词】《数与形》 数学思想 教学片段

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）29-0082-02

人教版数学六年级上册教材将“数学广角”中的《数与形》单独列为一个主题单元，目的是引导学生体会数形结合思想的直观性，培养学生观察、分析、推理以及解决问题的能力。但在学生的认知结构中，数是数、形是形，两者难以和谐统一。如何将数的问题转化成形的问题呢？教师应当从直观的图形表征中寻找计算方法，通过数与形之间的相互转换，让学生从中体会数与形都是表征问题的方式，由此打通形象思维与抽象思维之间的通道。沟通数与形之间的联系，可促使学生将知识内化于心、外化于形，使深度学习真正发生。下面，以特级教师叶柱执教的六年级上册《数与形》为例，探索以“数形结合”为基石，让学生在解决问题中真正体会到“寓数于形”“以形解数”“数形互补”的数与形之间的联系、发展与变化，促使学生在数与形之间的相互转换中，感悟数形结合的数学思想。

一、寓数于形

师：“1”这个数可以用哪一种“形”来表示？

生1：长方形、三角形。

生2：“1”可以表示一个圆形、正方形、平行四边形等。

师：你用了“等”字表示“1”，这表示还可以有很多不同的图形，那我们就选择其中一个代表吧，假如“1”用一个正方形来表示，那么“2”应该怎么表示？“4”怎么表示？“99”呢？

生3：“2”表示2个正方形，“4”表示4个正方形，“99”表示99个正方形。

师：同学们都知道不同的数字可以表示不同个数的正方形，那么，“1+3+5”这个算式可以用什么图形表示呢？请你将想到的图形在本子上画下来。

（图形展示如图1、图2、图3）

生4：我画了1个加3个、加5个小正方形。（如图1）

生5：因为1+3+5是一个等差数列，我就想到了可以用“金字塔”的图形。（如图2）

生6：我发现“1”是一个正方形，加上3个会组成一个更大的正方形，加上5个就会得到更大更大的一个正方形。（如图3）

师：从这三个图形中，我们发现了一个固定的算式，如果采用形来表示，可以有多种不同的表示方法。图3这样组成的图形与前面两种比较，好处在哪里呢？

生7：组成的图形是一个大正方形，很容易知道一共有3×3=9个，9=32。

师：那如果是1+3呢？1+3+5+7呢？请直接说出答案。

生8：1+3=4，1+3+5+7=16。

师：这里只有1+3+5的图形，你觉得加7，添上7个小正方形应该添在哪里呢？

[ ][ ][ ][ ][1=12][1+3=22][1+3+5=32][1+3+5+7=42]

生9：我认为上面加一排，右边加一排，可以组成一个更大的正方形。

生10：像他这样拼，可以拼成一个边长为4×4的正方形。

师：如果是1+3+5+7+9+11+13，请你计算一下答案。谁能用简洁的语言解释一下为什么是这个答案？

生11：答案是7的平方。因为按照这样的规律，2个数相加是2的平方，3个数相加是3的平方，以此类推，7个数相加就是7的平方。

师：你还能联系上面4×4的图形，推理得出1+3+5+7+9+11+13的图形吗？

【赏析】要实现数形结合，就要完成从数到形的转化，打通从数到形的“隔断墙”。先通过简单的数字“1”引导学生思考用哪一个形来表示，还有2，4，99呢？学生初步感知数与形的对应关系。接着引导学生思考，并画一画1+3+5这个算式可以用怎样的图形来表示，让学生构造形，体会形虽然有多种，但数与形却一一对应，感悟同样的形可以产生不同的计算方法，用不同的方式计算同一个几何量，达到用“数”来表示“形”，用“形”来理解“数”，感受数与形之间的联系、发展与变化。最后，引导学生联系图形推理1+3+5+7+9+11+13，想一想算式的结果和组成的圖形之间的联系，进一步激发他们探究规律的欲望。从数到式、从独立的形到组合的形，从多样化的形到呈正方形，层层递进、深入思考，学生体会到了“数中有形”，更加深入地感悟“形中有数”。

二、以形解数

师：这个“形”中还隐藏着其他的数的运算规律吗？（如下图形所示）口算：42-32等于几？

[ ][42-32=7 （4+3）  22-12=3 （2+1）

32-22=5 （3+2）  52-42=9 （5+4）]

生1：42-32=7。

师：请你对照图形观察，4的平方，3的平方，7分别对应什么图形？

生2：4的平方对应整个大正方形的个数，3的平方对应除了外面一圈小正方形，里面所有小正方形的个数，7指的是最外面一圈正方形的个数。

师：请继续计算：32-22，22-12。

生3：32-22=5，22-12=3。

师：那么52-42呢？请问这个图上有“5的平方”和“4的平方”吗？你能想象出算式与图形之间的联系吗？

生4（上台手指图形）：增加了大正方形外面的一圈，正方形的个数表示5的平方;原来大正方形内正方形的个数，表示4的平方;外面一圈正方形个数表示9个。

师：看看这四道算式，你有没有发现其中存在着什么规律？

生5：42-32=7，7=（4+3）;32-22=5，5=（3+2）;22-12=3，3=（2+1）。

师：你能指一指4+3，3+2，2+1各表示哪里的图形吗？

（生5上台指4+3，3+2，2+1所表示的图形，其余学生也用手书空比划）

师：根据这一规律，你能计算1002-992等于几，并想象算式与图形之间的聯系吗？

【赏析】要实现数形结合，还要完成形对数的反哺，搭建从形到数的“玄关墙”。“数”引导学生去探索规律，而“形”的出现提高了学生探索规律的效率。先让学生计算42-32，32-22，22-12分别等于几，并找一找所有数字分别对应什么图形，巧妙借助图形帮助学生理解算式中数的含义，为探索“数”的规律做好“形”的铺垫;接着学生找一找四道算式的规律，指一指“数”规律背后隐藏的图形，借助图形的直观性将抽象的数规律具体形象化，数形对照，算式与图形一一对应，培养学生寻找数与形的对应能力。如此教学，学生体会“数中思形”，更加深刻地感悟“以形解数”，再根据算式发现规律，并用图形来表达、验证规律，有利于学生反思建构，实现形象思维和抽象思维的互助互补、相辅相成。

三、数形互补

师：这个图形的涂色部分占整个正方形的几分之几？请用算式表示。（出示图4）

生1：[12]+[14]=[34]，涂色部分占整个正方形的[34]。

师：这里通过简单的计算就能得出结果，如果再加一块涂色部分呢？请你用一道算式来表示，并计算出结果。（出示图5）

生2：[12]+[14]+[18]=[78]，涂色部分占整个正方形的[78]。

师：这个[12]+[14]+[18]，能通过计算得到[78]，那么，你能联系图形，通过其他更简单的方法来说一说吗？

生3：将整个图形设为“1”，这个空白部分表示[18]，涂色部分也可以表示1-[18]=[78]，因此：[12]+[14]+[18]=1-[18]=[78]。

师：这位同学通过联系图形，从不同的视角解释计算的结果，想法更加巧妙。如果这个图形不断增加，你能写出一个算式，并很快得出计算结果吗？请试着写一写。（出示图6）

生4：[12]+[14]+[18]+[116]+[132]+[164]=[6364]。

师：你是如何快速知道计算结果是[6364]？

生4：因为最后的一块空白部分为[164]，那么，涂色部分只要1-[163]=[6364]就是各个涂色部分之和。

【赏析】数的运算离不开形的支撑，形的存在是让学生更加理解数的规则与运算方法。如果说“寓数于形”是顺向思维，那么“以形解数”就是逆向思维。在这一教学环节中，学生通过观察图形列出算式并计算结果，即把形的直观描述与数的精确刻画相结合体现“形中有数”，再利用计算结果联系图形找到更简洁的计算方法，发展到了“以数释形”。通过图形不断增加，设置“你能写出一个算式，并比较快地得到计算结果吗？你是如何快速知道计算结果是[6364]”这几个问题，让学生反思数与形的关系，进而在发现规律的过程中体会到：如果没有直观图形作思考的载体，学生很难发现和理解规律;只通过图形，不借助算式也难以建立计算结果与算式之间的联系，从而在形对数的直观性、数对形的深刻性两方面，构筑起数形结合的“承重墙”，发挥了数形互补的作用。

【作者简介】裘一能（2002— ），男，汉族，浙江嵊州人，现就读于绍兴文理学院，小教专业;裘迪波（1977— ），男，汉族，浙江嵊州人，现就职于浙江省嵊州市教育体育局教研室。

（责编 杨 春）