Limited-Budget Consensus Design and Analysis for Multiagent Systems With Switching Topologies and Intermittent Communications

Le Wang,Jianxiang Xi,Bo Hou,and Guangbin Liu

Abstract—This paper investigates limited-budget consensus design and analysis problems of general high-order multiagent systems with intermittent communications and switching topologies.The main contribution of this paper is that the tradeoff design between the energy consumption and the consensus performance can be realized while achieving leaderless or leaderfollowing consensus,under constraints of limited budgets and intermittent communications.Firstly,a new intermittent limitedbudget consensus control protocol with a practical trade-off design index is proposed,where the total budget of the whole multiagent system is limited.Then,leaderless limited-budget consensus design and analysis criteria are derived,in which the matrix variables of linear matrix inequalities are determined according to the total budget and the practical trade-off design parameters.Meanwhile,an explicit formulation of the consensus function is derived to describe the consensus state trajectory of the whole system.Moreover,a new two-stage transformation strategy is utilized for leader-following cases,by which the dynamics decomposition of leaderless and leader-following cases can be converted into a unified framework,and sufficient conditions of the leader-following limited-budget consensus design and analysis are determined via those of the leaderless cases.Finally,numerical simulations are given to illustrate theoretical results.

I.INTRODUCTION

DISTRIBUTED cooperative control of multiagent systems has received much attention from scholars due to its increasing applications in various technological fields,such as coordination of mobile robots,formation of multiple satellites,and synchronization of wireless sensor networks [1]–[5].Note that consensus problems should be tackled in the aforementioned applications,which refer to designing distributed controllers using local information such that a group of agents realize an agreement of some relevant states.Recently,some significant researches on the consensus of multiagent systems has been performed and many interesting works regarding consensus were reported in [6]–[9].

Due to the resource limitation,it is required that the control budget should be limited.In this situation,the consensus performance and/or the energy consumption should be optimized under limited budget constraints.It should be pointed out that the concept of the limited-budget consensus is inspired by the guaranteed-cost consensus,which is described as a suboptimal or optimal consensus problem.Recently,some researchers studied guaranteed-cost consensus problems and determined different guaranteed costs to depict upper bounds of cost indexes as shown in [10]–[14],where the cost budgets cannot be limited.Considering the impacts of the limited energy,Xiet al.[15] addressed energy-constraint output consensus problems for multiagent systems,where only the energy consumption is ensured without considering the consensus performance.Although the consensus in[10]–[15] were optimized,the limited budget constraints were not considered.In practical applications,because the total budget of the whole multiagent systems is usually limited,it is significant to investigate limited-budget consensus problems.Meanwhile,since both consensus performance and energy consumption are important indexes to optimize,it is important to realize their trade-offs with the limited budget.

Communication topologies play key roles in consensus problems,which may suffer some communication constraints in practical applications.On the one hand,since links of communication networks may change,the neighboring relationships among agents are time-varying,which can be described by switching topologies.In this scenario,communication topologies switch at some time points,so the Laplacian matrix of the whole topology is piecewise continuous as shown in [16]–[18] and the references therein.On the other hand,due to intermittent communications caused by the likes of network-injected packet losses,actuator failures,and temporary faults of sensing devices,the whole communication link will be interrupted and the control inputs of all agents will be zero during disconnected communication time intervals.Considering the influence of intermittent communications,consensus for second-order nonlinear multiagent systems with time delays and adaptive consensus for high-order delayed multiagent systems were studied in[19] and [20],respectively.An observer-based method was proposed to address the distributed robust consensus with intermittent communications in [21].Wenet al.[22] investigated consensus problems with both switching topologies and intermittent communications adopting tools of theM-matrix theory.

Based on communication patterns among agents,consensus can be divided into leaderless consensus and leader-following ones.For leaderless consensus,multiple agents share the neighboring state information to reach a collaborative behavior autonomously,which cannot be specified previously[23]–[25].It should be pointed out that a virtual leader,also called a consensus function,can describe the expected trajectory formed by agents in leaderless multiagent systems.Olfati-Saber and Murray [26] determined the consensus function by investigating the average-consensus problem for first-order multiagent systems.A consensus function was derived in [27] to show the macroscopic movement of leaderless high-order nonlinear multiagent systems as a whole.Moreover,there exists a real leader in leader-following multiagent systems,where the leader can be regarded as an objective to be tracked by followers.Several important breakthroughs on leader-following consensus were obtained in[28]–[31].Although many efforts have been made to investigate leaderless and leader-following consensus utilizing different methods,it is still significant to develop an approach that can study these two cases in a unified framework.

Motivated by the aforementioned works,this paper studies the limited-budget consensus problems of general high-order multiagent systems with intermittent communications and switching topologies,which is of great significance.Firstly,the achievement of the limited-budget consensus means that the agreement of all agents can be reached under the constraints of the total budget given previously,which has many potential important applications,including the cooperation of robots and quadrotors with limitations to their battery supply and oil tank capacity.Secondly,in practical applications,multiagent systems may be subject to communication constraints of intermittent communications and switching topologies,which may break down the operation of the whole system.By proposing the limitedbudget consensus protocol with these communication constraints,their effects to the multiagent systems will be well delt with.To the best of our knowledge,the following three problems are still worthy of investigation:1) Realizing the trade-off design between consensus performances and energy consumptions with limited budgets;2) Determining the impacts of both intermittent communications and switching topologies on the limited-budget consensus;3) Unifying leadless and leader-following consensus in a same framework.

In this paper,firstly,we propose leaderless and leaderfollowing intermittent limited-budget consensus protocols,respectively,where the intermittent relative state information among switching neighbors is utilized and the value of the trade-off design index is required to be less than the limited total budget.Then,we study leaderless and leader-following consensus in the unified framework.In this framework,the dynamics of the whole multiagent system is decomposed into two parts: its consensus dynamics and disagreement dynamics,which describe the consensus state trajectory and the relative movement among agents,respectively.For leaderless consensus,this decomposition is achieved by an orthonormal transformation,and an explicit formulation of the consensus function is determined for the consensus dynamics.Leaderless limited-budget consensus design and analysis criteria are given in the form of linear matrix inequalities(LMIs).For leader-following consensus,a new two-stage transformation approach is developed for the decomposition.In this case,the dynamics of the leader is used to describe the consensus dynamics,and sufficient conditions of the leaderfollowing limited-budget consensus design and analysis are derived.

Compared with existing works regarding the optimized consensus,the results in this paper are new in three aspects.Firstly,the practical trade-off design between energy consumptions and consensus performances is realized with a limited total budget.In this scenario,limited-budget consensus design and analysis criteria are derived,where matrix variables of LMIs are partly determined according to the total budget and practical trade-off design parameters.The total budget could not be limited in [10]–[14] and the trade-off design was not considered in [15].Secondly,the impacts of both switching topologies and intermittent communications are considered in consensus design and analysis,which is challenging since the trade-off design index becomes a piecewise continuous integral function and the relative state information among agents is intermittent.In contrast,switching topologies and intermittent communications were not involved simultaneously in [10]–[15].Thirdly,leaderless and leader-following consensus are achieved in a unified framework,where leader-following limited-budget consensus design and analysis criteria are obtained via the main results of the leaderless consensus,adopting a new two-stage nonsingular transformation approach.However,leaderless and leader-following consensus were not be unified in [10]–[15].

The remainder of this paper is arranged as follows.In Section II,basic concepts of the graph theory,types of communication constraints,and the consensus protocol modeling are presented.Section III gives the leaderless limited-budget consensus design and analysis criteria,and determines an explicit formulation of the consensus function.In Section IV,the main results of leaderless cases are extended to leader-following cases via a two-stage nonsingular transformation approach.Section V provides two numerical simulation examples to demonstrate the effectiveness of the theoretical results.The main work is summarized in Section VI.

Notations:N represents the set of natural numbers.Rdand Rd×ndenote the real column vector and real matrices of dimensionsdandd×n,respectively.Let 1Nbe anNdimensional column vector with its entries being 1.The transpose and the inverse matrix ofAare indicated byATandA−1,respectively.M=MT>0 means that the matrixMis symmetric and positive definite.INdenotes the identity matrix of the dimensionN.0,0dand 0d×nrepresent zero numbers,ddimensional zero column vectors andd×n-dimensional zero matrices,respectively.The notation ⊗ is used to denote the Kronecker product.The symbol ∗ stands for the symmetric terms of a symmetric matrix.

II.PROBLEM FORMULATION

A.Communication Topology Modeling

B.Communication Constraint Analyzing

In this paper,we consider the influence of both switching topologies and intermittent communications,which is analyzed by the following three steps.

Firstly,it is assumed that there exists a sequence of uniformly nonoverlapping time intervalswithwhereis bounded and topologies switch at time pointt˜r.Note that the communication among agents is always connected,which means that each undirected graph is connected or each directed graph contains a spanning tree.

Thirdly,in virtue of the above analysis,we can suppose that t here exists a sequence of uniformly bounded nonoverlapping time intervalsand an integerrpsuch thatandwitht0=0 andLetrepresent the disconnected communication rate withIt can be found that both switching topologies and intermittent communications occur over time intervals [tp,tp+1);that is,topologies are switched by the switching signal δ(t) in time intervalsand communications among all agents are disconnected in time intervals(see Fig.1 for illustration).

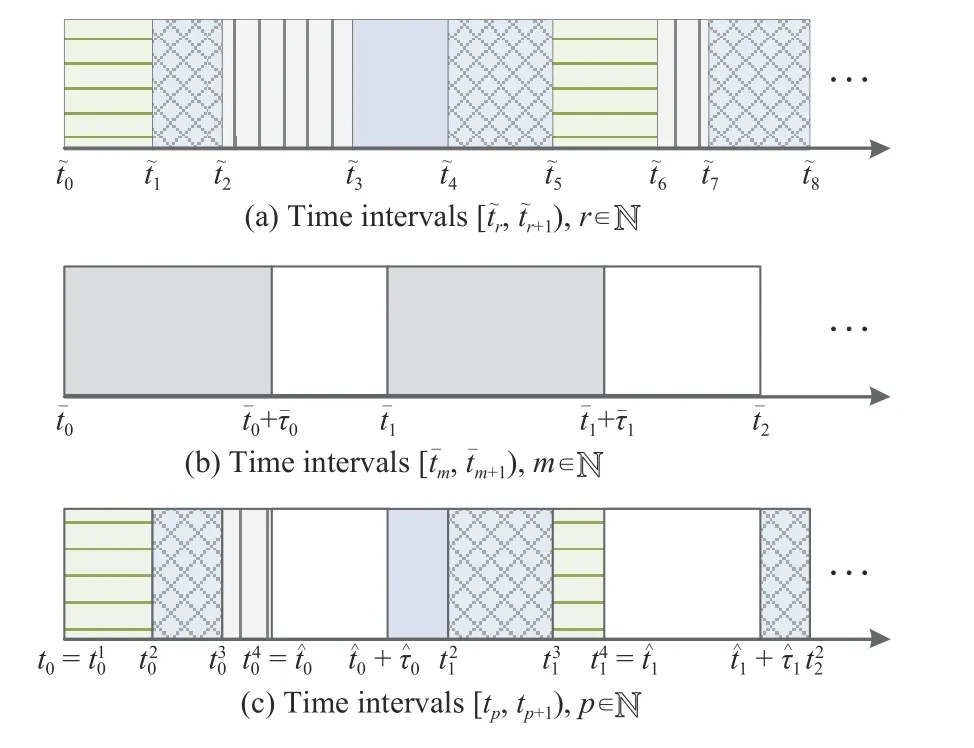
Fig.1.Examples for communication constraints.

C.Leaderless Consensus Protocol Designing

Consider a general high-order multiagent system consisting ofNhomogeneous agents,where the dynamics of theith agent is modeled as follows:

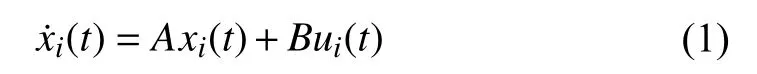
wherei∈{1,2,...,N},xi(t)∈Rdandui(t)∈Rnare the state and the control input,respectively.A∈Rd×dandB∈Rd×nare system matrices,and it is assumed that the pair(A,B) is stabilizable.

According to the analysis of communication constraints,we propose a new limited-budget consensus protocol with switching topologies and intermittent communications in the following form:

withp∈N,M=MT>0 andQ=QT>0 representing the practical trade-off design parameters.Kudenotes the gain matrix,andJis the practical trade-off design index between the energy consumption and the consensus performance.Allowing ψ to be the total budget of the whole multiagent system,then we can give the following definition of the leaderless limited-budget consensus design for multiagent systems with switching topologies and intermittent communications.

Definition 1:For any given bounded non-identical initial statesxi(0)(i=1,2,...,N) and total budget ψ>0,multiagent system (1) is said to be leaderless limited-budget consensualizable by protocol (2) if there exist a gain matrixKuand a bounded vector-valued functionc(t)∈Rdsuch that limt→+∞(x(t)−1N⊗c(t))=0NdandJ≤ψ,wherec(t) is called the consensus function.

The control objectives of this paper are twofold:1) Designing the gain matrixKusuch that multiagent system (1) with switching topologies and intermittent communications reaches leaderless limited-budget consensus,and determining an explicit formulation of the consensus function.2) Extending the main results of the leaderless limited-budget consensus to the leader-following case.

Remark 1:The proposed protocol (2) contains two new features.Firstly,the limited total budget ψ is considered as a significant performance constraint for multiagent systems and protocol (2) should be designed to ensure that the value ofJis less than the total budget ψ.In this case,it is challenging to determine the interaction mechanism of matricesMandQon the gain matrixKu.Secondly,Jis a piecewise integral function due to the impact of intermittent communications.It should be noted that both the energy consumption and the consensus performance affectJin the connected communication time intervalswhile only the consensus performance has an impact onJin the disconnected communication time intervalsIn this scenario,Jis a piecewise continuous integral function since bothJx(t)andJu(t) have the piecewise continuous right-hand sides caused by intermittent communications and switching topologies.Compared with the consensus protocols of[10]–[15],the advantages of the proposed consensus protocol are twofold.On the one hand,the practical trade-off design index is introduced to weigh the energy consumption against the consensus performance under the limited budget constraint,while on the other hand,the proposed consensus protocol can be utilized in the situation that both switching topologies and intermittent communications are involved.However,the proposed consensus protocol may contain some deficiencies; that is,there exists potential chattering phenomenon caused by the piecewise continuous right-hand sides of the consensus protocol,which we will address in future works.

III.LEADERLESS LIMITED-BUDGET CONSENSUS DESIGN AND ANALYSIS CRITERIA

In this section,we first propose leaderless limited-budget consensus design and analysis criteria with both switching topologies and intermittent communications,and then determine an explicit formulation of the consensus function to describe the consensus state trajectory of the multiagent system as a whole.

Substituting the control inputui(t) of (2) into (1),we can obtain that

By inequation (21),we can find thatwhich indicates that multiagent system (1) reaches consensus exponentially.

In the following,we will discuss the impact of the limited budget on the gain matrixKuin accordance with the practical trade-off design indexJ.From (2),we can obtain that

Theorem 1 gives a method to design the gain matrix of protocol (2) such that multiagent system (1) with switching topologies and intermittent communications is limited-budget consensualizable.Next,the limited-budget consensus analysis criterion is provided when the gain matrix of protocol (2) is given.By adopting the convex property of LMIs and lettingwe can derive the following corollary directly from Theorem 1.■

Corollary 1:For any givenKuand ψ >0,multiagent system(1) with protocol (2) reaches leaderless limited-budget consensus ifand there exists a matrixP=PT>0such that

In the sequel,we will determine an explicit formulation of the consensus function to describe the macroscopical motion trajectory of the whole multiagent system.From (8),Definition 1 and the fact thatwe can obtain that

According to (6),(31) and (32),the following corollary can be obtained.

Corollary 2:If multiagent system (1) reaches limitedbudget consensus with protocol (2),then an explicit formulation of the consensus function is described as

Remark 3:In Theorem 1,the conditionshows the interaction mechanism of the total budget ψ on the matrix variablewhich is associated with the initial states.Note that in the practical application of the state feedback control,the initial states of the multiagent system should be available.In this case,the conditioncan be easily satisfied by providing a proper total budget ψ.It is also noted that the initial states are supposed to be non-identical to derive this condition,which is a mild and reasonable assumption since consensus is reached when states of multiagent systems are agreed,and the consensus control is no longer required in this case.It should also be noted that the practical trade-off design between energy consumptions and consensus performances is achieved by establishing the relationship between the matrix variableand the matricesMandQ.In this case,MandQrepresent the weight of the consensus performance and the energy consumption,respectively,and one can adjustMandQto realize the trade-off design.Moreover,can be estimated by the Gersgorin disc theorem in [33] and Theorem 2.2 in [34],respectively.

Remark 4:To address the intermittent communication problem,two parameters are introduced.The first one is the nominal convergence rate α,which can guarantee that the convergence rate of the Lyapunov function is faster than α in connected communication time internalsp∈N.The second one is the maximum divergency rate β,which undertakes that the Lyapunov function is divergent with a rate no more than β over disconnected communication time internalsp∈N.By introducing these two parameters,the conservativeness of the method can be reduced by a more rigorous scaling of the time derivative of the Lyapunov function than the methods found in [10]–[15].In this sense,multiagent system (1) can reach consensus exponentially with a convergence rate faster thanaccording to inequation (21).However,the methods in [10]–[15] can only reach the asymptotical consensus without intermittent communications and switching topologies.Note that ifwhich means that the communication is continuous,then the conditionin Theorem 1 becomes α>0.In this case,multiagent systems without intermittent communications reach consensus exponentially with a convergence rate faster than α by designing a proper gain matrixKuby Theorem 1 without the term

Remark 5:Consensus function plays an important role in consensus problems since it describes the macroscopical motion trajectory of the whole multiagent system.The consensus function of the average consensus problem is the average of the states of all agents,i.e.,which was proposed by Olfati-Saber and Murray [26].For first-order multiagent systems,the consensus function is the average value of initial states of all agents,if the communication topology is balanced and strongly connected.According to Definition 1 and Corollary 2,it can be found that the consensus function for high-order multiagent systems is associated with both the average value of initial states of all agentsand the matrix exponential functioneAt.In this case,since the communication topology is undirected and connected,the consensus function can be regarded as the zeroinput response of the average of initial states of all agents,which is similar to that of the average consensus.However,if the communication topology is directed,then the consensus function can be determined by the initial state of each agent with an oblique projector as shown in Theorem 3 of [35],which is different from that of the average consensus.

IV.ExTENSION TO LEADER-FOLLOWING CASES

In this section,we give the leader-following limited-budget consensus design and analysis criteria for multiagent systems with switching topologies and intermittent communications.

Allowing agentNto be the leader and the otherN−1 agents to be the homogenous followers,then the multiagent system with the leader-following structure is described as

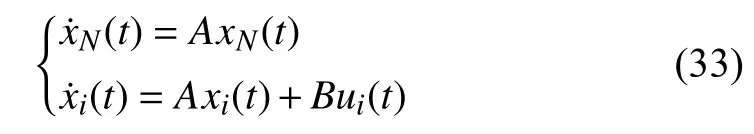
wherei=1,2,...,N−1.In system (33),the leader is located at the root vertex of the spanning tree;that is,there exist one or more directed communication channels from the leader to its followers.It is supposed that the leader never receives state information from followers and the communication channel among followers is undirected.It can be seen from (33) that the dynamics of the leader can be utilized to determine the consensus function,which is tracked by followers.

We propose the leader-following limited-budget consensus protocol as follows:

p∈N,W=WT>0,R=RT>0 andKulrepresenting the gain matrix.The definition of the leader-following limited-budget consensus design for multiagent systems with switching topologies and intermittent communications is given as follows.

Definition 2:For any given bounded non-identical initial statesxi(0)(i=1,2,...,N−1) and total budget ψl>0,multiagent system (33) is said to be leader-following limitedbudget consensualizable by protocol (34),if there exists a gain matrixKulsuch that1,2,...,N−1)andJl≤ψl.

Next,we develop a two-stage transformation method to decompose the whole dynamics of system (35) with leaderfollowing structure into the consensus dynamics and the disagreement dynamics.

Firstly,we give the nonsingular transformation to convert the Laplacian matrixLδ(t) into a block diagonal matrix.Define a nonsingular matrix as follows:system (33) with protocol (34) reaches leader-following limited-budget consensus ifand there exists a matrixF=FT>0 such that

Remark 6:In this paper,we investigate leaderless and leader-following limited-budget consensus in a unified framework of the dynamics decomposition.For leaderless cases,we construct an orthonormal transformation to decouple the dynamics of the whole multiagent systems into two linearly independent parts due to the symmetry of Laplacian matrices for undirected topologies.For leader-following cases,since the Laplacian matrices are asymmetric,the aforementioned orthonormal transformation is no longer valid.To facilitate the analysis of the leaderless and leaderfollowing cases in a unified framework,we proposed a twostage nonsingular transformation approach,where the first stage is to deal with the asymmetry of Laplacian matrices by a nonsingular transformation.In this case,the Laplacian matrices can be transformed into diagonal block matrices with the blockand 0.Then,in the second stage,we diagonalize the blockby the orthonormal transformation such that the dynamics of the whole multiagent systems can be linearly decoupled.

Remark 7:According to the two-stage nonsingular transformation approach,limited-budget consensus design and analysis criteria are derived in Theorem 2 and Corollary 3,respectively,which are similar to the main results of leaderless cases obtained in Section III.However,the main differences between leaderless cases and leader-following cases are two-fold.Firstly,the communication topology structures of multiagent systems (1) and (33) are different.System (1),with the leaderless structure,describes the dynamics of each agent,where all agents decide their collaborative behavior collectively.However,system (33)with the leader-following structure describes the dynamics of the leader with no control input and that of the follower,where the consensus state of followers is determined by the state of the leader.Secondly,the interaction mechanism matrices between the practical trade-off design indexes (2)and (34) are different.For leaderless cases,the interaction mechanism matrixis the Laplacian matrix of a c[omplete graph ]while it is a Laplacian matrix,i.e.,of a star graph for leader-following cases(see Fig.2 for illustration).From Fig.2,it can be found that all agents play equal roles in determining the interaction mechanism of the practical trade-off design index for the leaderless cases,but it is determined solely by the leader for the leader-following cases.

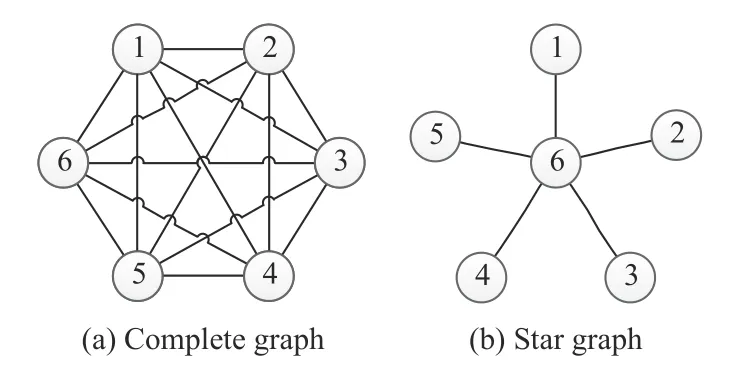
Fig.2.Examples for complete graph and star graph.

V.NUMERICAL SIMULATIONS

In this section,two simulation examples are provided to illustrate the efficacy of the theoretical results obtained in the previous sections.

Example 1 (Leaderless Cases):

Consider a leaderless multiagent system consisting of six agents,where the switching communication topologies and the switching signal withTd=0.3 s are shown in Figs.3 and 4,respectively.Without loss of generality,the adjacent matrices of topologies are chosen as 0–1 ones.Set the system matrices of each agent as

The initial states of multiagent system (1) are chosen as

Fig.3.Switching communication topology set for leaderless cases.

Fig.4.Switching signal for leaderless cases.

The connected and disconnected communication time intervals are set ast∈[0.6p,0.6p+0.48)s andt∈[0.6p+0.48,0.6(p+1))s(p∈N),respectively.In this scenario,the parameters in Theorem 1 are given asand β=8.The practical trade-off design parameters areM=diag{0.04,0.02,0.05,0.03} andQ=0.15.The provided total budget is ψ=300.According to Theorem 1,it can be calculated by the feasp solver of the LMI toolbox in MATLAB that κ=0.0311 and

Then,we can design the gain matrix of protocol (2) asKu=[−0.1436,0.4186,0.7249,0.4675].

Fig.5 shows the state trajectories of six agents and the consensus function,where the states of the agents are denoted as full curves and the trajectory of the consensus function is represented by a sequence of circles.The trajectory of the practical trade-off design index and the total budget are shown in Fig.6.

It can be found from Fig.5 that the states of six agents converge to the same value formed by the consensus function,which describes the macroscopical movement trajectory of the whole multiagent system.Note that the small bulges in the state curve of each agent reflect the impacts of the intermittent communications and switching topologies.Fig.5 indicates that the consensus can be achieved under the communication constraints.The curves in Fig.6 show that the value of the practical trade-off design index converges to a finite value that is less than the total budget,which means that the limited budget constraints are satisfied.It can be concluded by the simulation results that leaderless multiagent system (1) with switching topologies and intermittent communications is limited-budget consensualizable by consensus protocol (2).

Fig.5.State trajectories of six agents and the consensus function.

Example 2 (Leader-Following Cases):

Consider a group of agents with one leader and five followers,where the disconnected communication time intervals are set ast∈[0.6p+0.45,0.6(p+1))s(p∈N) with the upper bound of the disconnected communication rate beingThe system matrices are given as follows:

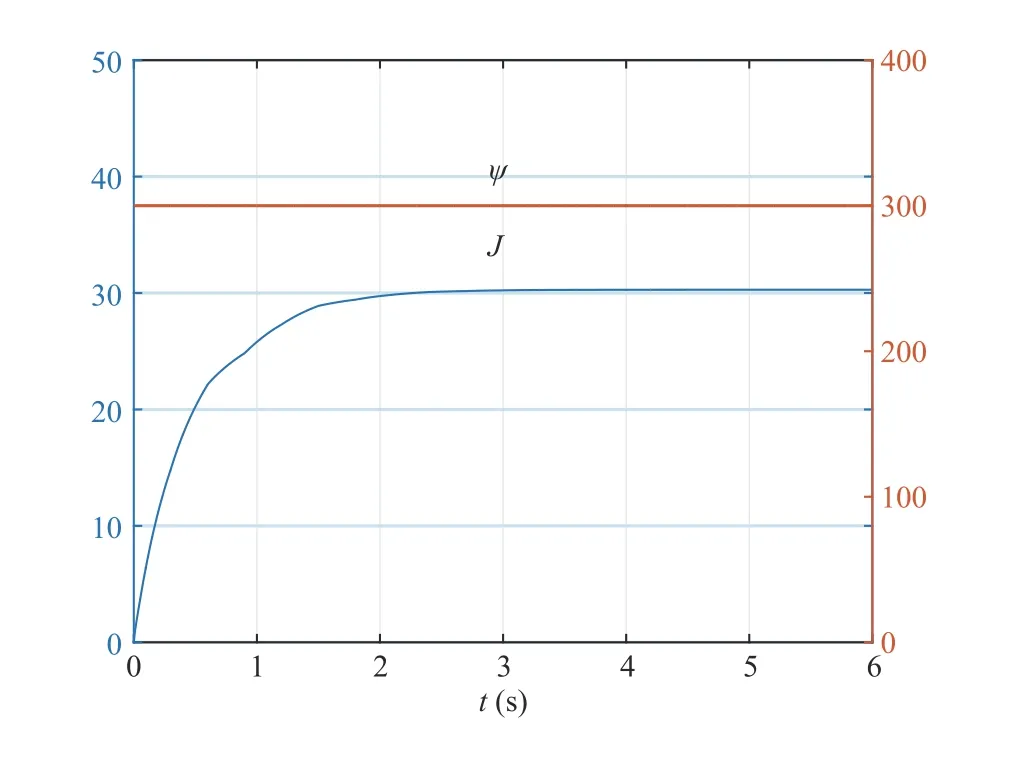
Fig.6.Trajectories of the practical trade-off design index and the total budget for leaderless cases.

The switching communication topology set is shown in Fig.7 by 0–1 weighted graphs,and the switching signal with the dwell time beingTd=0.3 s is described in Fig.8.Letx6(0)=[−6.5,−2.4,−5.4,−3.1]Tfor the leader,and the initial states of five followers are given as

Let α=2 and β=6.The values of the practical trade-off design parameters are set asM=diag{0.03,0.04,0.01,0.02}andQ=0.08,respectively.Let ψl=2500,then it can be determined according to Theorem 2 that κ=0.0092 and

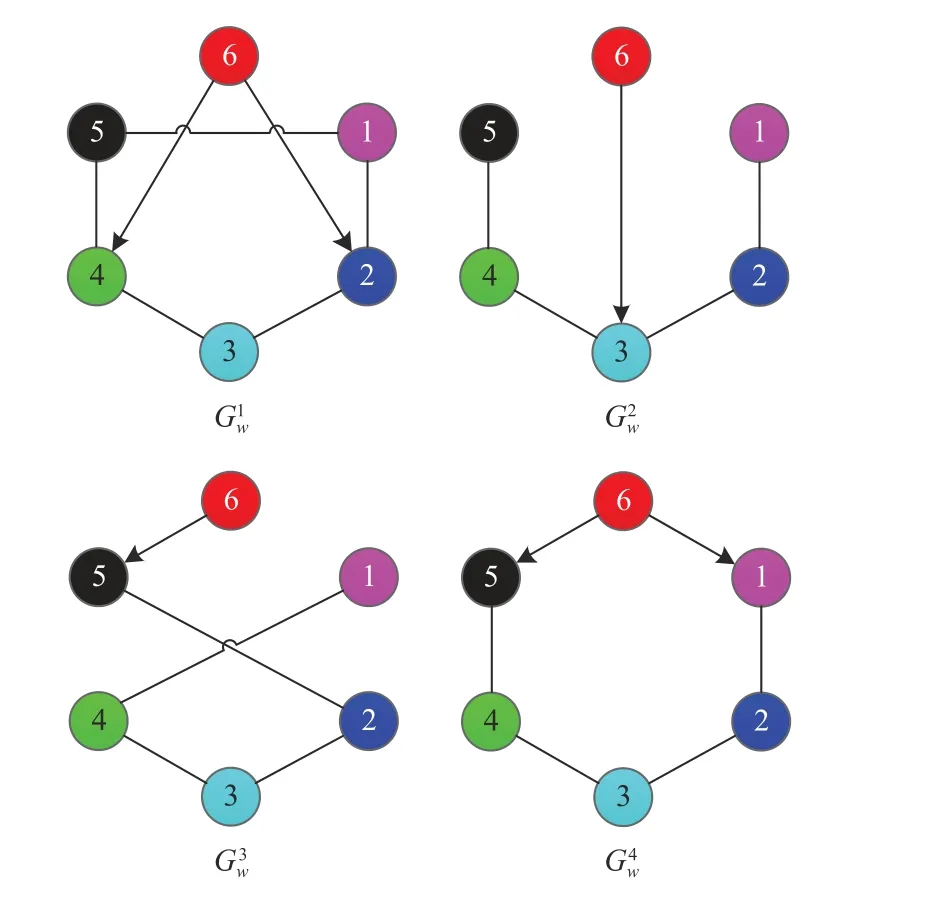
Fig.7.Switching communication topology set for leader-following cases.

Fig.8.Switching signal for leader-following cases.

In this case,we can design the gain matrix of protocol (34) asKu=[−0.1678,0.4299,2.2709,1.3618].

Fig.9 depicts the state trajectories of the leader and five followers,where the states of the leader and followers are described as sequences of circles and full curves,respectively.Fig.10 shows the curves of the practical trade-off design index and the total budget,respectively.

From Fig.9,it can be seen that state the curves of the five followers converge to that of the leader,where the state of the leader determines the consensus trajectory of the multiagent system as a whole.The influence of the intermittent communications and switching topologies can also be found in the state trajectories of the followers.Fig.10 indicates that the value of the practical trade-off design index converges to a finite value that satisfiesJl<ψl.The results in Figs.8–10 illustrate that for previously given total budgets,leaderfollowing multiagent system (33) with switching topologies and intermittent communications is limited-budget consensualizable by consensus protocol (34).

Remark 8:There are two main differences between the simulation results of the leaderless case and the leaderfollowing case.The first one is that the structures of the Laplacian matrices of these two cases are different.For the leaderless case,the Laplacian matrix is symmetric.However,the Laplacian matrix of the leader-following case is asymmetric,and all the elements of the row related to the leader are zero ones,since the indegree of the leader is zero.The second one is that the descriptions of the consensus trajectory of the whole multiagent system are different.For the leaderless case,the consensus trajectory is depicted by the consensus function,but it is described by the state trajectory of the leader for the leader-following case.

VI.CONCLUSIONS

Fig.9.State trajectories of one leader and five followers.

Fig.10.Curves of the practical trade-off design index and the total budget for leader-following cases.

Both leaderless and leader-following limited-budget consensus design and analysis problems were addressed in a unified framework for multiagent systems with switching topologies and intermittent communications.Leaderless and leader-following intermittent limited-budget consensus protocols with trade-off design indexes between consensus performances and energy consumptions were proposed,where the trade-off design index was required to be less than the limited total budget.An orthonormal transformation and a two-stage nonsingular transformation were proposed to decouple the dynamics of the whole multiagent systems into two linearly independent parts for leaderless and leaderfollowing cases,respectively.For leaderless cases,limitedbudget consensus design and analysis criteria were given,and an explicit formulation of the consensus function was determined.For leader-following case,the consensus dynamics was determined by the dynamics of the leader,and sufficient conditions of limited-budget consensus design and analysis were derived.

Future works will focus on extending the current work by adopting an event-triggered mechanism to address the limitedbudget event-triggered consensus design and analysis problems for multiagent systems with intermittent communications,and some interesting event-based dynamic feedback methods as shown in [36] also serve as inspiration.