Theory and Experiments on Enclosing Control of Multi-Agent Systems
2021-10-25YihuiWangYanfeiLiuandZhongWang
Yihui Wang,Yanfei Liu,and Zhong Wang
Abstract—This paper proposes a control strategy called enclosing control.This strategy can be described as follows:the followers design their control inputs based on the state information of neighbor agents and move to specified positions.The convex hull formed by these followers contains the leaders.We use the single-integrator model to describe the dynamics of the agents and proposes a continuous-time control protocol and a sampled-data based protocol for multi-agent systems with stationary leaders with fixed network topology.Then the state differential equations are analyzed to obtain the parameter requirements for the system to achieve convergence.Moreover,the conditions achieving enclosing control are established for both protocols.A special enclosing control with no leader located on the convex hull boundary under the protocols is studied,which can effectively prevent enclosing control failures caused by errors in the system.Moreover,several simulations are proposed to validate theoretical results and compare the differences between the three control protocols.Finally,experimental results on the multi-robot platform are provided to verify the feasibility of the protocol in the physical system.
I.INTRODUCTION
COOPERATIVE control has been widely researched due to its potential application in both military and civilian fields [1]–[3].As a type of engineering system,cooperative control can be characterized as a group of agents with autonomous functions connected through network topology,using their state information and limited inter-agent communications to complete complex tasks.According to the dynamics of the control object,cooperative control can be classified into first-order agent cooperative control [4],[5],second-order agent cooperative control [6],[7],high-order agent cooperative control [8],[9],heterogeneous agent cooperative control [10],[11],nonlinear agent cooperative control [12]–[14],etc.According to the control task,the cooperative control can also be classified as consensus control[15]–[17],formation control [18]–[20],flocking [21],[22],containment control [23]–[27],etc.The theoretical basis for solving these problems has become the cornerstone of solving other cooperative control problems.
Cooperative control mainly studies the cooperative work of various agents in a multi-agent system.On the other hand,the interaction between multi-agent systems is often involved in some scenarios,for example,using robots for shepherding,or using a group of robots to surround another group of robots.Due to the rivalry of the game,the robots do not send their information to the opponent but obtain the information of opponents through their sensors.Therefore,we define robots as followers and opponents as leaders.To further expand the generality of the problem,we assume that the number of opponents is greater than or equal to one.Here,we propose a control strategy calledEnclosing Control.The control strategy process can be described as followers designing their control inputs based on neighbor agent information,where the motion forms a convex hull,which contains the surrounded leaders.
Enclosing control and containment control have certain similarities.The containment control process is one where followers design their control inputs based on the information of neighboring agents,and move into the convex hull formed by the leader.It can be seen that enclosing control and containment control have the following differences:i) The leaders in the containment control are agents that form a convex hull,while the leader in the enclosing control is the surrounded object.ii) Followers in containment control enter into the convex hull through movement,while followers in enclosing control form the convex hull through movement to contain the leaders.iii) The primary relationship between the leaders and followers in the containment control is cooperation.In contrast,the relationship between the two types of agents in the enclosing control is mainly confrontation.
Although there are many differences between containment control and enclosing control,many theories in containment control can be used in the feasibility analysis process of enclosing control problems.Nowadays,due to the application potential of containment control,it has become a research hotpot.In [24],which used an integrator model to describe the dynamics of an agent,aStop-Gostrategy was proposed to guarantee that swarm systems with stationary/dynamic leaders achieve containment.The work in [25] proposed a control protocol based on consensus theory and gave topological requirements to achieve containment control.This paper provides a reference protocol design method for enclosing control requirements.In [26],continuous-time protocols and sampled-data based protocols were proposed and divided the theoretical analysis into two parts:system convergence analysis and topology design that ensure containment.This analysis method provides a reference analysis method for enclosing control.The containment control problem of continuous-time and discrete-time swarm systems with general linear dynamics under directional topology was studied in [23].The above works and some other works in the field build the basic framework for containment control research.They also provide an essential reference for enclosing control research.
As another important branch in collaborative control,the formation control process can be described as agents designing their control input according to the information of the neighboring agents and the vector describing the prescribed formation and the prescribed formation under control.A consensus-based distributed formation control was proposed in [28].The algorithm makes the agents come into agreement on the time-varying position and direction of the virtual center.This method provides a way to solve the problem of enclosing control of an isolated target by agents.In [29],a distributed control law without a virtual center is designed for linearized systems,and it is proved that the required relative altitude/position can be successfully achieved,and its heading angle can be synchronized.This scheme needs to design an algorithm when closing the target so that the formation stays around the target.A solution for relative positioning and formation control was proposed in [30].In this scheme,the agents estimate the relative position of their neighbors in realtime and use the estimated value to calculate their control inputs and drive them to reach the prescribed formation.This method can solve the enclosing control of the swarm system with dynamic leaders by designing the relative positions of the agents in the formation in advance.The work in [31] designed a formation control scheme based on a virtual leader for multiagent systems with first-order dynamic characteristics.By setting the virtual leader according to the status information of the leaders,and setting the relative position between the virtual leader and the follower,enclosing control over multiple targets can be achieved.
By setting the vector describing the prescribed formation or setting additional control algorithms,formation control can solve part of the enclosing control problem.However,there are still some problems using formation control to solve the enclosing control problem:i) In formation control,the virtual leader or leader is generally in motion.In order to use formation control to solve the enclosing control problem of multi-agent systems with stationary leaders,it is necessary to make the formation stay around the target and surround the target.ii) When using formation control in the enclosing control problem of multi-agent systems with multi-targets,it is necessary to know the state information of all the objects to design a predetermined formation that encloses all the targets.
The contribution of this paper mainly includes the following:i) This paper proposes a control strategy calledenclosing control.In this control strategy,the leaders and followers are primarily confrontational,which is very different from the collaborative relationship between the two types of agents in [23]–[27].ii) We designed a continuoustime protocol and a sampled-data based protocol.iii)Moreover,we analyzed and obtained the parameter requirements for the system to achieve convergence,and analyzed the topological conditions of the system to achieve enclosing control.
The outline of this paper is as follows:We list some related definitions and results in Section II.In Section III,we provide stability analysis of systems with network topology under the action of continuous-time control protocols.The stability of the system under the influence of the sampled-data based protocol is analyzed in Section IV.In Sections V and VI we give some simulation and experiment results,respectively.Then,we give a conclusion in Section VII.
II.PRELIMINARY
Some related concepts and results are introduced in this section.The detailed descriptions can be obtained from [5],[32]–[35].
A.Graph Theory

B.Notations,Definitions,and Lemmas
Notations:letInbe the identity matrix with dimensionn.i is the imaginary unit.Suppose a complex number λ ∈C,thenIm(λ),Re(λ),and |λ| denote,respectively,the imaginary part,the real part and the modulus of λ .ρ(A) denotes the spectral radius ofA.
Definition 1:Suppose that there is a finite set of pointsx1,...,xn∈Rm.The convex hull of the set of points is the minimal convex set,which contains all pointsxi,i=1,...,n,denoted by co{x1,...,xn}.Particularly,co{x1,...,xn}=
Definition 2:In a two-dimensional plane,suppose that there are a finite set of pointsx1,x2,...,xnand a pointyin the convex hull formed by the point set,y=k1x1+k2x2+···+knxn,n>2 holds.Assume thatmis the number of coefficients satisfyingki>0.Whenm≤2,it is said that the pointyis located on the boundary of the convex hull.
Lemma 1 (Geršgorin Disc Theorem):LetB=[βij]∈Cn×n.Then all the eigenvalues ofBare located in the union ofndiscs
Lemma 2 ([33]):Assume that the convergence radius of the power seriesisr.If a square matrixAsatisfies ρ(A)
In enclosing control,the surrounded targets/agents and the agents whose motion forms the convex hull are defined as leaders and followers,respectively.This paper considers the enclosing control of a multi-agent system with stationary leaders.Similarly,[5],[26],[36] investigate the containment control of a multi-agent system with stationary leaders.Without considering the velocity of the stationary leaders,a single-order integrator can be used to describe the dynamic model of the agent.Referring to [5],[26],[36],we assume that the system hasnagents,and use the single-integrator model to describe the dynamics of the agents.

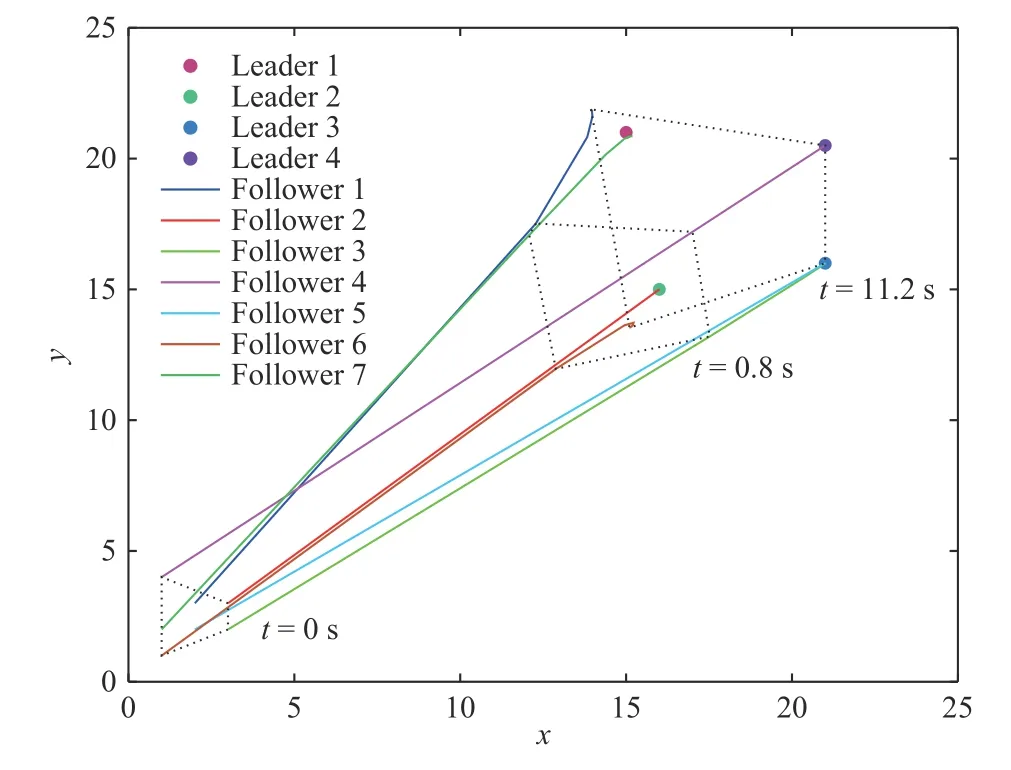
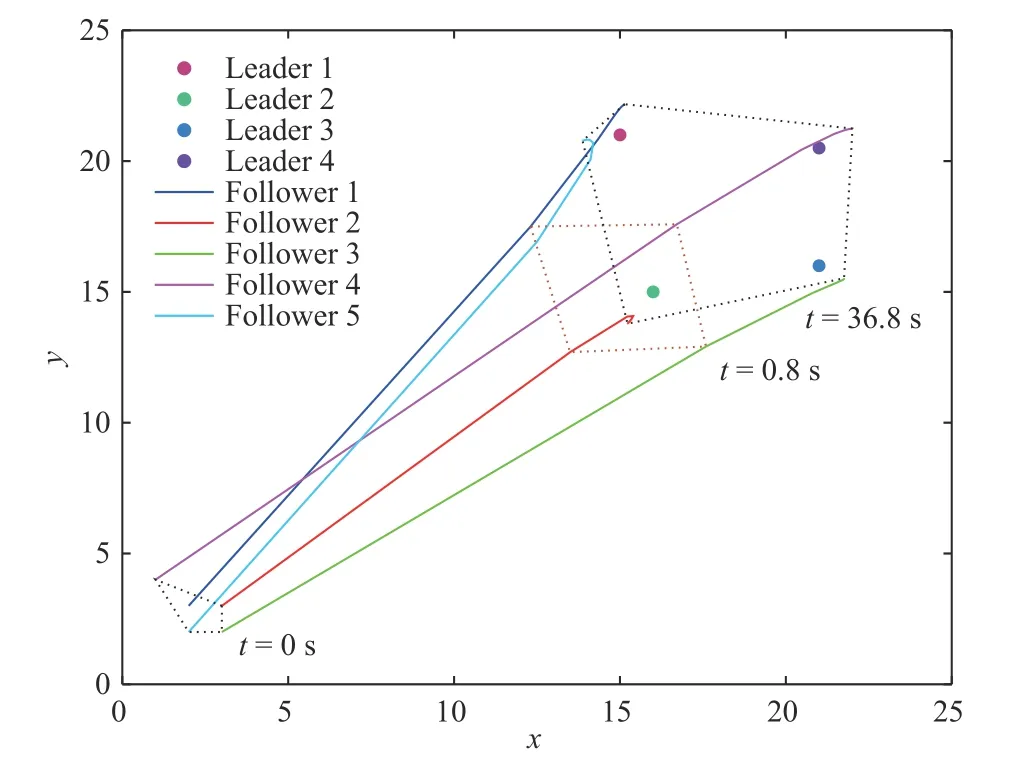
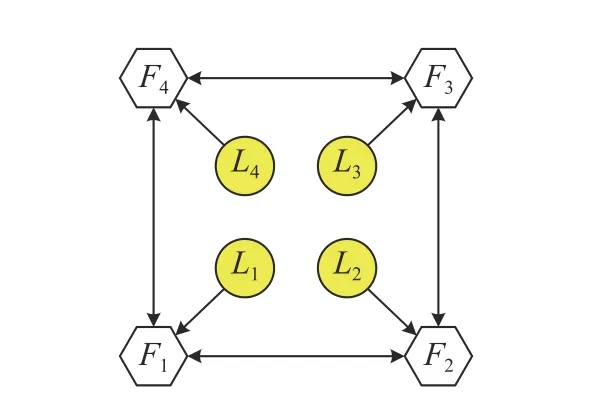
wherexi(t),ui(t)∈RNdenote,respectively,the state and the control input ofi-th agent.Among thenagents,magents are leaders andm Remark 1:In the enclosing control system,as mentioned above,then−mfollowers design their control inputs based on the information of neighboring agents,and the motion forms a convex hull,which contains themleaders.While in [23]–[27],n−mfollowers enter the convex hull formed by the leaders through control. We design the following enclosing control protocol for (1) as: whereLis the Laplacian matrix.According to the definitions of leaders and followers,LandEcan be,respectively,partitioned as The next lemma shows the gain requirements for the system to achieve convergence. WhenxF(+∞) has a convergent solution,all the eigenvalues ofFFFshould have positive real part.LetLiidenote diagonal elements in rowiofL,thenFrom the expression ofFFFand Lemma 1,we can get that α must satisfy Because each follower only receives the state information of one leader,and there are no isolated leaders in the communication topology,FFRis column full rank,and we can obtain that for anyi,i=n−m+1,...,n,there is a numberk,k=1,...,n−m,such that From Definition 1,we know that all leaders passively enter the convex hull spanned by the dynamic followers.■ Remark 2:When α increases in the value range,the radius of the smallest circumscribed circle of the convex hull decreases.Particularly,when α=0,all positions of followers converge to that of leaders. Remark 3:Because in the application of the physical system,it is rare to use fewer followers than the leaders to surround the leaders,this paper assumesn−m≥min Section II.Whenn−m Corollary 1:When the topology is fixed,andmaxi∈FUsing (2) for (1),in a 2-D space,there are no leaders on the convex hull boundary if all followers receive state information from the other two or more followers,and each follower in the system receives information for one leader state only,and there is no isolated leader in the communication topology. Proof:The expression of any leader in the agents can be written as Case 1:When the convex hull requires all followers to form,since all followers receive state information from two or more leaders,there are at least three elements in γ1,γ2,...,γn−mthat are not zero.And γ1,γ2,...,γn−msatisfiesfrom Definition 2,so all the followers are not on the convex hull boundary. Case 2:When the convex hull only needs to be composed ofsfollowers,ands When γs+1,...,γn−m=0,the leader is inside the convex hull.When at least one number in γs+1,...,γn−mis not zero,then there are at least three coefficients inxp=ηp1x1+···+ηpsxst hat are not zero.Therefore,at least three coefficients in the expression ofxkare not zero.By calculation,we can obtain that From Definition 2,all the leaders are not on the convex hull boundary.■ Remark 4:The significance of studying this special enclosing control is that when a leader is on the boundary of t he convex hull,the leader can escape the convex hull with a small movement,and this enclosing control can prevent this. We discretize the protocol (2),so the sampled-data based protocol can be written as whereh>0 is the sampling period andk=0,1,...are the sampling instants.By using the protocol (20) for (1),the Then,the conclusions of Lemma 4 can be obtained.■ From the proof of Theorem 1,we have the following theorem. Theorem 2:Suppose that the directed network topology is fixed,withandh<2.Using (20) for(1),dynamic followers form a convex hull that contains all leaders for arbitrary initial positions if each follower in the system receives one leader state information only,and there is no isolated leader in the communication topology. Proof:The verification is similar to that of Theorem 1.■ From the proof of Corollary 1,we can obtain the following corollary. Corollary 2:When the topology is fixed,α<0 andh<2.Using (20) for (1),in a 2-D space,there are no leaders on the convex hull boundary if all followers receive state information from the other two or more followers,and each follower in the system receives one leader state information only,and there is no isolated leader in the communication topology. Proof:The verification is similar to that of Corollary 1.■ We present several simulations in this section,which to validate the previous theoretical results and compare the differences between containment control,formation control,and enclosing control.In simulations,assume that the elements of the weighted adjacency matrix are all 1 or 0.When there is an edge of a leader (or follower) pointing to a follower,the corresponding element is 1;otherwise,it is 0. In the simulation,we do not consider the rotation of agents.Then,each dimension of the state space of the agent is independent.Considering the enclosing control of the multiagent system on a two-dimensional plane,based on the dynamic model assumption (1),the dynamic model of the agent can be obtained as follows: wherexixandxiyare,respectively,x-axis andy-axis coordinates of the agents,anduixanduiyare the control input ofx-axis andy-axis ofi-th agents,respectively. When a group of agents with four leaders and seven followers are considered.Li,Fidenote the leaders and followers,respectively. Example 1:When the fixed network topology is chosen as in Fig.1.From Theorem 1,we can obtain −0.25<α<0.We choose α=−0.1.Set the simulation time to 0 to 50 seconds.The simulation result is shown in Fig.2.The convex hull formed by the final positions of the movement of the followers contains the leaders,and Leader 4 on the boundary of the convex hull. Example 2:Still consider Fig.1.From Theorem 2,by calculation,we can obtain −0.25<α<0 andh<2.We choose α=−0.15 andh=0.8.We set the simulation time to 0 to 50 seconds.The result using (20) for (1) is shown in Fig.3.The conclusion is consistent with the continuous-time situation. Fig.1.A topology with four leaders and seven followers. Fig.2.Trajectories of all the agents in Example 1. Fig.3.Trajectories of all the agents in Example 2. A group of agents with four leaders and five followers with a fixed interaction pattern is chosen as shown in Fig.4,whereLiandFidenote the leaders and followers,respectively.Each follower in the topology has at least two follower neighbors and receives state information of one leader only,and there is no isolated leader in the communication topology.The topological graph satisfies the conditions of Theorem 1,Theorem 2,Corollary 1,and Corollary 2. Fig.4.A topology with four leaders and five followers. Example 3:When the interaction pattern is chosen as in Fig.4,from Theorem 1,we can obtain that −0.25<α<0.We choose α=−0.2 and set the simulation time from 0 to 50 seconds.The simulation result is shown in Fig.5.It is obvious that all the leaders passively enter the convex hull formed by the final position of the movement of the followers. Fig.5.Trajectories of all the agents in Example 3. Example 4:Consider Fig.4.From Theorem 2,by calculation,we can obtain −0.25<α<0 andh<2.We choose α=−0.12 andh=0.8 and set the simulation time from 0 to 50 seconds.The result using (20) for (1) is shown in Fig.6.It is known from Fig.6 that the final position of the movement of the followers forms the convex hull,which contains all leaders. Fig.6.Trajectories of all the agents in Example 4. The works in [26] proposes the following containment control protocol for a multi-agent system with single-order integrator dynamics.The simulation result is shown in the simulations in [26].The simulation results show that the followers enter the convex hull formed by the leaders.It can be seen from the results that the containment control is not suitable for enclosing control problems. A formation control strategy is proposed in [31].Using an artificially designed convex hull shape,when topological conditions are met,formation control can solve some enclosing control problems.However,the convex hull needs to be designed according to the leader.This process is cumbersome,while the control strategy proposed in this paper only requires information about the parameters that control the size of the convex hull. We experimentally validate the proposed enclosing control algorithms on a multi-robot platform in this section.Experiments were performed using an omnidirectional wheeled robot to obtain results.Next,this paper briefly introduces the experimental platform we developed. The platform we developed consists of eight robots equipped with the control program;each robot has four omnidirectional wheels,an ultra wide band (UWB)positioning system,and a control station,as shown in Fig.7.The hardware of the robot is developed based on the Smallsize Football Robot.The shape is approximately a cylinder with a diameter of 18 cm,the battery life is 11 minutes,and the overall weight is 3.184 kg.The controller is developed based on STM32F407 with a clock frequency of 72 MHz.The attitude of robot is estimated by MPU6050.The UWB system with an accuracy of 5 cm of circular error probable is used to obtain the position and speed of the robot,and the output rate is 10 Hz.The main controller measures the wheel speed with high-precision encoders and uses the proportional-integralderivative (PID) algorithm to control the motors.A 1 GB micro secure digital memory (SD) card is onboard for data recording.The compass board sends the direction information from the compass to the control station through the Serial to the nRF24L01 (NRF) module.The control station sends instructions to control the coordinate system of robot to align with that of the UWB system.The control station software is developed based on Python3.7 in the Windows10 environment.It can obtain the operating parameters of the robot from the UWB positioning base station,Serial to NRF network,and send control instructions to the robot.Fig.8 describes the hardware structure of the multi-agent platform. In order to realize the control of multiple robots under different communication topologies,we have designed a control software that can be divided into two layers.The top layer is responsible for setting the communication topology,implementing the control protocol,robot positioning,and coordinate system alignment.The bottom layer is accountable for the collection and transmission of sensor data,and the speed PID loop control of the robots. Because the acceleration process of the robot takes a short time and can be ignored,its movement process can be regarded as uniform motion.Then,the first-order integrator can be used to describe the dynamic model of robot,and the control input is speed.When the coordinate system of robot is aligned with that of the positioning system,(26) can be used to describe the robot dynamics model.We use this model to describe the dynamics of all robots. Fig.7.Multi-robot platform.The robot can be set as a leader or follower by setting the communication topology. Fig.8.The hardware structure of platform.Mainly includes the UWB positioning system,compass alignment system,robot system,and control station. When the leaders are close to the convex hull boundary,due to the existence of positioning errors,it is easy to cause the failure of the enclosing control.Design the topology,as shown in Fig.9.Li,Fidenote the leaders and followers,respectively.Each follower in the topology has at least two follower neighbors.The topology satisfies the conditions of Corollary 2.Using (20),by calculation,we can determine that−0.25<α<0 andh<2.Leth=0.8.The simulation results and experiment results are shown in Fig.10.In the experiments,the UWB positioning system uses distance units in centimeters,and the experiment results correspond to that of simulations.We then get two results: 1) The convex hull formed by the dynamic followers contains the leaders,and there are no leaders in the boundary of the convex full,which is consistent with the results in Corollary 2. Fig.9.A communication topology with four leaders and four followers. Fig.10.Trajectories of the eight mobile robots using (20).The simulation and experiment time is 0 to 51 s. 2) When α is increased within the range of value,the radius of the smallest circumscribed circle of the convex hull decreases. The interaction between multi-agent systems is often involved in some scenarios.Therefore,this paper proposes a control strategy called enclosing control.We used directed graphs to describe the direction of information exchange between robots and proposed a continuous-time and a sampled-data based protocol.We analyzed the requirements of the gain parameters to ensure the convergence of the system and the topological requirements to ensure achieving enclosing control.Then,we studied the special case of no leader on the convex hull boundary under the influence of the two protocols.Some simulation results are proposed to verify the theoretical derivation results.Then some simulations are given to compare the differences between containment control,existing solution,and the methods proposed in this paper.Simulation results show that enclosing control is more concise in protocol design than formation control.Finally,the experimental results on a multi-robot platform are given.The experimental results show that the minimum circumscribed circle radius of the convex hull becomes smaller as the gain parameter increases. In this paper,the setting of the gain parameter uses the information of the Laplacian matrix.It essentially uses the information of all agents.In practical applications,the follower cannot always obtain the information of the entire system,so the agent can only achieve enclosing control by making the parameter approach zero.This will reduce the size of the convex hull and increase the probability that the enclosing control fails because of measurement and control error.There have been many examples in the literature of fully distributed control of multi-agent systems.Our future work will refer to related research results to design fully distributed enclosing control protocols.Besides,we only study multi-agent systems with universal first-order integrator dynamic models.We will consider enclosing control of second-order,high-order,and nonlinear systems in our future work.III.ANALYSIS FOR CONTINUOUS-TIME PROTOCOL





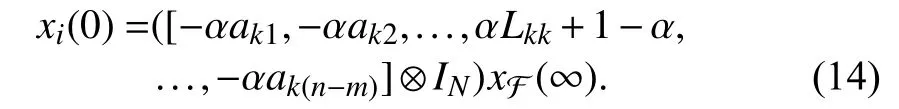



IV.ANALYSIS FOR SAMPLED-DATA BASED PROTOCOL


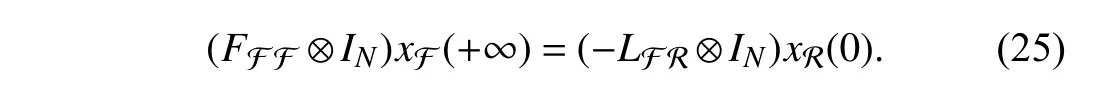
V.SIMULATIONS





VI.ExPERIMENTAL VALIDATION



VII.CONCLUSION
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems:Applications and Trends
- Adaptive Memory Event-Triggered Observer-Based Control for Nonlinear Multi-Agent Systems Under DoS Attacks
- Vehicle Motion Prediction at Intersections Based on the Turning Intention and Prior Trajectories Model
- Command Filtered Finite/Fixed-time Heading Tracking Control of Surface Vehicles
- Hierarchical Reinforcement Learning With Automatic Sub-Goal Identification
- Variational Gridded Graph Convolution Network for Node Classification
