Adaptive Memory Event-Triggered Observer-Based Control for Nonlinear Multi-Agent Systems Under DoS Attacks
2021-10-25XiangguiGuoDongyuZhangJianliangWangandChoonKiAhn
Xianggui Guo,Dongyu Zhang,Jianliang Wang,,and Choon Ki Ahn,
Abstract—This paper investigates the event-triggered security consensus problem for nonlinear multi-agent systems (MASs)under denial-of-service (DoS) attacks over an undirected graph.A novel adaptive memory observer-based anti-disturbance control scheme is presented to improve the observer accuracy by adding a buffer for the system output measurements.Meanwhile,this control scheme can also provide more reasonable control signals when DoS attacks occur.To save network resources,an adaptive memory event-triggered mechanism (AMETM) is also proposed and Zeno behavior is excluded.It is worth mentioning that the AMETM’s updates do not require global information.Then,the observer and controller gains are obtained by using the linear matrix inequality (LMI) technique.Finally,simulation examples show the effectiveness of the proposed control scheme.
I.INTRODUCTION
NOWADAYS,multi-agent systems are widely used in various fields,such as unmanned aerial vehicles,power systems,sensor networks,etc.[1]–[4].However,as networks evolve,the problem of network security becomes more prominent [5]–[7].Since multi-agent systems (MASs) work in networked environments,they are vulnerable to cyber attacks,which may cause system performance degradation or even instability [8].Hence,the security problems of MASs have attracted the research interest of many scholars in the control field [8]–[10].In multi-agent networks,agents may be subjected to denial-of-service (DoS) attacks,stealthy deception attacks,replay attacks,false data injection attacks,etc.[11],[12].Among these attacks,the DoS attack scenarios can be divided into two types;the first type affects the cyberphysical network (which is constituted of a physical layer with fixed physical links and a cyber layer with cyber control units)to prevent the prompt update of the control inputs,and the other type destroys the communication network within the cyber layer to affect the communication topology graph,which would hinder the information interaction among agents[13];thus,they are more destructive than other attacks [14].To resist DoS attacks,there are existing results on solving security problems for MASs [15]–[21].Persis and Tesi [15]studied the input-to-state stability (ISS) of networked systems,and clearly described the frequency and duration of DoS attacks under ISS for the first time.Based on this work,in[16]–[19],the secure consensus problem of MASs under DoS attacks was analyzed,and constraint conditions on DoS attack frequency and duration were obtained under guaranteed consensus.It should be noted that most previous works only consider the security of linear MASs.However,in practice,real systems are essentially nonlinear [22]–[24],and the study of nonlinear systems is more challenging.Moreover,although some results,such as those in [20],[21],consider the security consensus of nonlinear MASs,they generally require that all system states are measurable.Nevertheless,full system states are often challenging to obtain in most practical applications[24]–[27].Therefore,the observer-based feedback control is often used.Furthermore,in practice,it is generally believed that external disturbances in the system are the main underlying cause of performance degradation and even instability [28].Due to the growing demand for high-accuracy performance under external disturbances,disturbance compensation control approaches have been widely applied in the control community due to their powerful ability to reject disturbances [29],[30].The composition of the state observer with the disturbance compensation mechanism and the design of an observer-based anti-disturbance controller under DoS attacks make the secure consensus control problems of MASs highly complicated and challenging.Hence,how to design an observer-based anti-disturbance controller for nonlinear MASs under DoS attacks is the main motivation of this article.
Another problem in multi-agent networks is limited communication bandwidth.In contrast to the traditional timetriggered mechanism,the event-triggered mechanism (ETM)is based on pre-set conditions to determine whether the transmission and control tasks are executed,which can reduce the collection and transmission of redundant data and save network resources [31].Therefore,the consensus problem for MASs based on ETM has been widely studied [21],[32]–[34].In [21],an event-based consensus control scheme is proposed for MASs under cyber attacks by using fixed threshold parameters in the event triggering scheme,which may cause significant consumption of communication resources.A centralized event triggering scheme is presented in [32],in which all agents are triggered at the same time.This method reduces the design difficulty but requires global information,and will result in unnecessary usage of communication and computing resources.A distributed adaptive event triggering strategy is adopted in [33],[34],where the threshold can be adjusted dynamically with the system state,and only the information of it and its neighbors are needed to update.As a result,network resources are saved and it is a good choice for ameliorating the event triggering strategy.Certainly,reducing the communication burden will inevitably lead to the decline of system performance.Therefore,how to dynamically adjust the number of trigger points to improve system performance based on reducing the communication burden is another motivation of this article.
Considering the above discussion,the main difficulties are summarized as follows:a) how to design a more accurate state observer and a more effective controller under DoS attacks and disturbance to achieve consensus for nonlinear MASs and b) how to design an ETM based on reduced communication resources to improve system performance.To solve these problems,this paper studies the event-triggered security consensus problem for nonlinear MASs under DoS attacks,and the main contributions are as follows:
1) An Anti-Disturbance Control Scheme Based on a Novel State Observer:Compared with the observer design scheme proposed in [25],[26],by embedding a buffer in the state observer,the state of the previous moment can be stored;thus,the observer accuracy can be improved in the presence of DoS attacks.Unlike [25],[35] where the control signal is set to zero when DoS attacks occur,the proposed observer-based controller can reduce the impact of packet loss caused by DoS attacks due to the existence of the buffer,which can provide a more reasonable control signal and improve the security and reliability of MASs.
2) A Novel Adaptive Memory Event-Triggered Mechanism(AMETM):In contrast to the adaptive ETM studied in [33],[34],by storing recently received information,we can dynamically adjust the number of trigger points to improve system performance and reduce the occurrence of error triggered events caused by sudden changes due to erroneous measurements.Meanwhile,its threshold can be adjusted with state changes for the purpose of saving network resources,and the design process is considerably simpler than that of the memory ETM in [36],[37].Moreover,a hybrid update mechanism is used to eliminate Zeno behaviors.
3) The Compensation Mechanism for the Observer and Controller:In contrast to [38] in which a disturbance observer is used based on the state feedback control technique to resist disturbances,the proposed compensation mechanism can effectively reduce the difficulty caused by unmeasurable states and resist the influence of disturbances.In addition,the consensus performance of the system can be improved.
The remaining sections of this article are organized as follows.Section II introduces the system description and some preliminaries.The main results are given in Section III.Simulation examples in Section IV illustrate the feasibility and effectiveness of the proposed method.Finally,conclusions and future work directions are presented in Section V.
The following notations are used throughout this article: Rn,RN×N,and N denote then-dimensional space,N×Nreal matrices,and set of positive natural numbers,respectively;INrepresents the identity matrix of dimensionN;and 1Ndenotes theN×1 matrix with all ones.The superscript“T”is used to represent the transpose of a matrix.Let diag{·} be a diagonal matrix and colThe Euclidean norm and union are denoted as ‖·‖ and ∪,respectively.For a symmetric matrixM,M>0(≥0) orM<0 denotes that the matrixMis positive definite (positive semidefinite) or negative definite,respectively,and its maximum and minimum eigenvalues are denoted by λmax(M) and λmin(M),respectively.In addition,to facilitate the calculation,we give the definition of Kronecker product below.IfM=[mij]∈Rα×βandN=[nij]∈Rp×q,then the Kronecker productM⊗N∈Rαp×βqis the block matrix

II.PROBLEM STATEMENT AND PRELIMINARIES
Fig.1 depicts the structure of theith agent under DoS attacks,which mainly consists of sensor,actuator,controller,buffers,zero-order hold (ZOH),AMETM,and observer.When the AMETM picks out state variables that need to be sampled,these data are transmitted to observers and controllers over the network.If DoS attacks occur,the data transmission will be blocked,which will adversely affect the system stability and performance.
A.Graph Theory
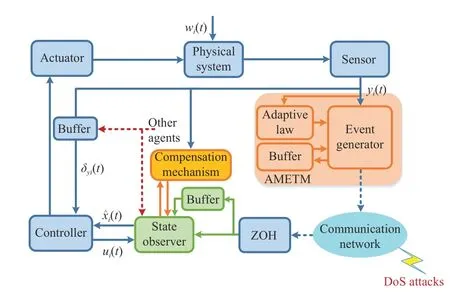
Fig.1.Framework of the ith agent under DoS attacks.
The multi-agent system is assumed to have an undirected topology G=(V,E) where V={1,...,N} is the node set and E ⊆V×V is the edge set.Each agent is represented by a node.In graph G,if nodesiandjcan exchange information with each other,then nodejis a neighbor of nodeiand vice versa.Let Ni={j∈V|(j,i)∈E,j≠i} represent the set of neighbor nodes of nodei,and A=[ai j]∈RN×Nbe the adjacency matrix,whereai j=1 if(j,i)∈E,which means that agentican receive information from agentj;otherwise,aij=0.For an undirected graph,(j,i)∈E implies(i,j)∈E.Furthermore,define the degree matrixD=diag{d1,...,dN}∈RN×Nwiththen,the Laplacian matrix L is denoted by L=D−A.For the fixed undirected graph G,its Laplacian matrix L is a symmetric matrix with eigenvalues satisfying 0=λ1(L)<λ2(L)<···<λN(L).For brevity,λ2(L)and λN(L) will be denoted respectively as λ2and λNin the rest of this paper.
B.System Model
Consider a nonlinear MAS ofNagents with the dynamics of theith agent being given by

wherexi(t)∈Rn,ui(t)∈Rb,yi(t)∈Rq,andwi(t)∈Rdare the state,input,output and external disturbance of theith agent,respectively.f(xi(t),t)=col{f1(xi(t),t),...,fn(xi(t),t)}∈Rnrepresents the nonlinear dynamics of theith agent.Furthermore,A,B,C,D,andFare known matrices with appropriate dimensions,and ΔAis a time-varying uncertain matrix.Suppose that rank(B)=rank(B,D)=b.
Assumption 1:The pair (A,B) is stabilizable,the pair (A,C)is observable,and matrixCis of full row rank.
Assumption 2:There exists a positive constantϖand a matrixE(t),such that

E(t)ET(t)E(t)≤IN
where time-varying matrix satisfies .
Assumption 3:There exists a matrix Λ such that∀x1(t),x2(t)∈Rn,the nonlinear functionf(xi(t),t) satisfies

Assumption 4:The disturbance signalwi(t) is bounded,i.e.,whereis a known upper bound of the disturbance signal.
Remark 1:Assumption 1 is common in many existing results [10],[25],[39].Assumption 2 is a constraint condition for the uncertainties that may be caused by mismatched parameters,inaccuracies in the model,etc.[40].The mild Lipschitz condition in Assumption 3 describes a class of nonlinear systems,such as robot systems.In fact,all linear functions and piecewise time-invariant continuous functions also satisfy this assumption [41],[42].
C.DoS Attack Model and AMETM
In this paper,as shown in Fig.1,we only consider DoS attacks that affect the updating of the controller,i.e.,the first type of DoS attacks mentioned in the introduction section,which prevents the transmission of sensor data by destroying the communication channel from sensors to observers.It affects the updating of the observer and controller.In addition,under DoS attacks,each agent may be attacked at any time.In practice,however,it is impossible for an attacker to launch a continuous attack because it needs to gather energy for the next attack.Next,to facilitate the analysis,the relevant definitions of DoS attacks are given below.
Let {hk}k≥0be a time sequence of DoS attacks,where thekth DoS time interval is Hk=[hk,hk+ηk) withhk+1>hk+ηk,in whichhkis the instant when thekth DoS attack starts,and ηk>0indicates the duration of thekth attack.Over the time interval [t0,t),let Φ(t) denote the time period set,where communication is subjected to attack,and let Ψ(t) denote the time period set,where communication is allowed.Then,

In addition,to describe the influence of DoS attacks on trigger points,we give the following definition.
Definition 1 (Communication Failure Frequency [32]):For∀t>t0,letn(t0,t) denote the total number of trigger points under attack during [t0,t) for each agent.Then,the frequency of attack on trigger points ℓ(t0,t) over [t0,t) is defined as

Remark 2:In order to distinguish between a DoS attack and package dropout,the differences are summarized as follows:1) The number of packet losses usually belongs to an integer set,and the number of continuous packet losses is usually a small number,while the DoS attack may last for a long period of time.For example,when the communication failure frequency is less than a certain value,the considered DoS attacks may include the case in which the network is blocked for a certain period of time.However,this case usually does not fall into the category of packet loss owing to the fact that the continuous packet loss is less than a small number.2)From 1),we know that the developed method is effective when the communication failure frequency is smaller than a certain value.Thus,as long as a class of packet losses meet this condition,the developed mathematical framework is also applicable for addressing issues related to this class of packet losses.Note that such a framework for dealing with packet loss has not been used in the existing literature;therefore,it is also a new method in the area of handling packet loss.

wherep∈N denotes the number of data stored in a buffer.Then,in contrast to the traditional event triggering scheme,a novel AMETM is proposed as follows:
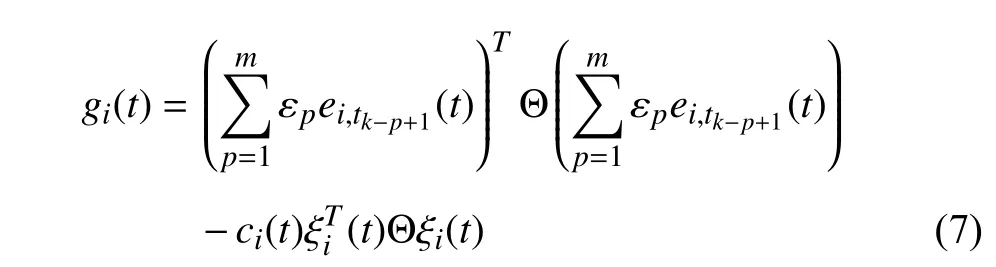

Remark 3:Compared with the centralized event triggered condition designed by accumulating all agent errors in [32],this paper adopts the event triggered condition (7) that requires neighboring agents only.This can effectively reduce unnecessary communication.Differently from the traditional event triggered condition [21],recently triggered packets are also used by adding a buffer of sizemto (7).Note that the latest released packet is more important,so the choice of ε1should be larger than the other εp’s.By adjusting the value of εp,we can change the number of trigger points.A smaller ε1and a largermwill trigger more points to ensure system performance.When ε1=1 andm=1,the event triggering scheme degenerates to a normal adaptive trigger mechanism,as in [33].In addition,the trigger speed depends onci(t).The smallerci(t) is,the more triggers there are but the better the system performance is.Alternately,the largerci(t) is,the fewer triggers there are but the worse the system performance is.Obviously,the larger the number of triggers,the heavier the communication burden.Moreover,whenci(t)=0,the event triggering scheme becomes a time triggering mechanism.Therefore,the choice ofci(t) should be a tradeoff between system performance and communication burden.
To avoid Zeno behavior,similarly to [17],[32],the next triggered instant is determined as follows:

whereσis a given positive constant.
In this study,undirected communication networks are considered,and the control objective is to design a control strategy based on observation information to ensure that the multi-agent system (1) can achieve consensus in the presence of DoS attacks and disturbance,i.e.,
Furthermore,to achieve the purpose of this article,the following Lemmas are necessary.
Lemma 1 [32]:For a positive definite functionV(t),if it satisfies:
whereαandρare unknown positive constants,andts+1is the next trigger instant with the latest successful trigger instant beingtswhent∈[tk,tk+1) andtk∈Φ(t).Then,the following inequality holds:
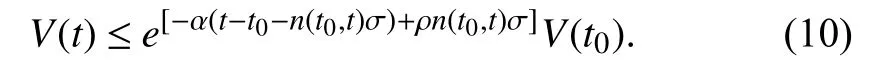
Lemma 2 [24]:For a matrix equality constraint,i.e.,PB=BN,it can be transformed into a standard linear matrix inequality and be rewritten approximately as

whereνis an arbitrarily small positive constant.
III.MAIN RESULTS
In this section,an anti-disturbance control strategy based on a state observer is proposed,which improves the observer accuracy by storing the previous data in a buffer and compensating for the uncertainty and disturbance.The secure consensus of the multi-agent system subject to external disturbances and DoS attacks is analyzed,and the conditions for ensuring consensus are given.In addition,the problem of coupling observer and controller gains with unknown matrix variables is solved by using the linear matrix inequality (LMI)technique.Finally,Zeno behavior is excluded for all agents.
A.Design of Observer and Controller
The state observer for theith agent is constructed as below:


B.Consensus Analysis
To simplify the notation,denote the state estimation errorThen,it follows from (1) and (15) that
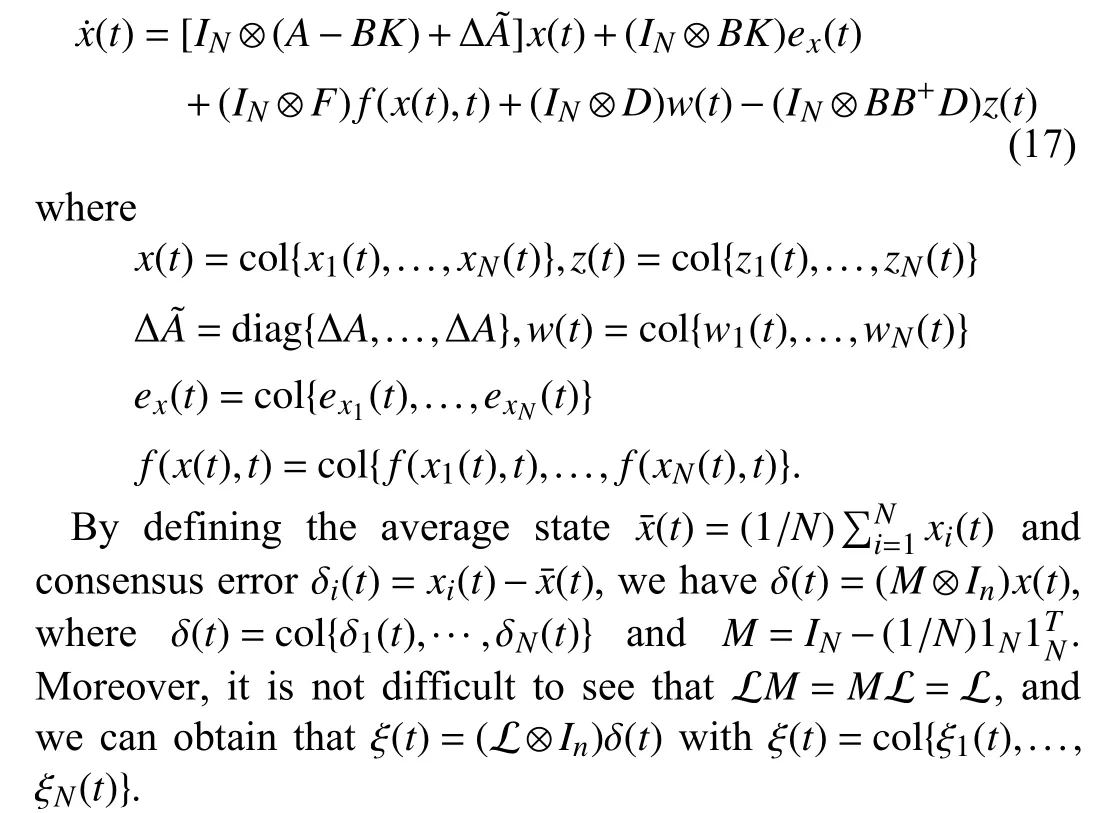
Then,based on the above definitions and (17),the dynamic of the consensus error δ is given by

Next,the main results of this article are presented in the following theorem.
Theorem 1:Suppose that Assumptions 1–4 hold.Under the observer-based anti-disturbance controller (15) and the triggering function (7) with the triggering sequence (9),MAS(1) can achieve consensus and the designed observer (12) can give accurate estimate of the state in the presence of DoS attacks and external disturbances,if there exist symmetric positive definite matricesP1,P2and matricesL,K,W,andW1satisfying
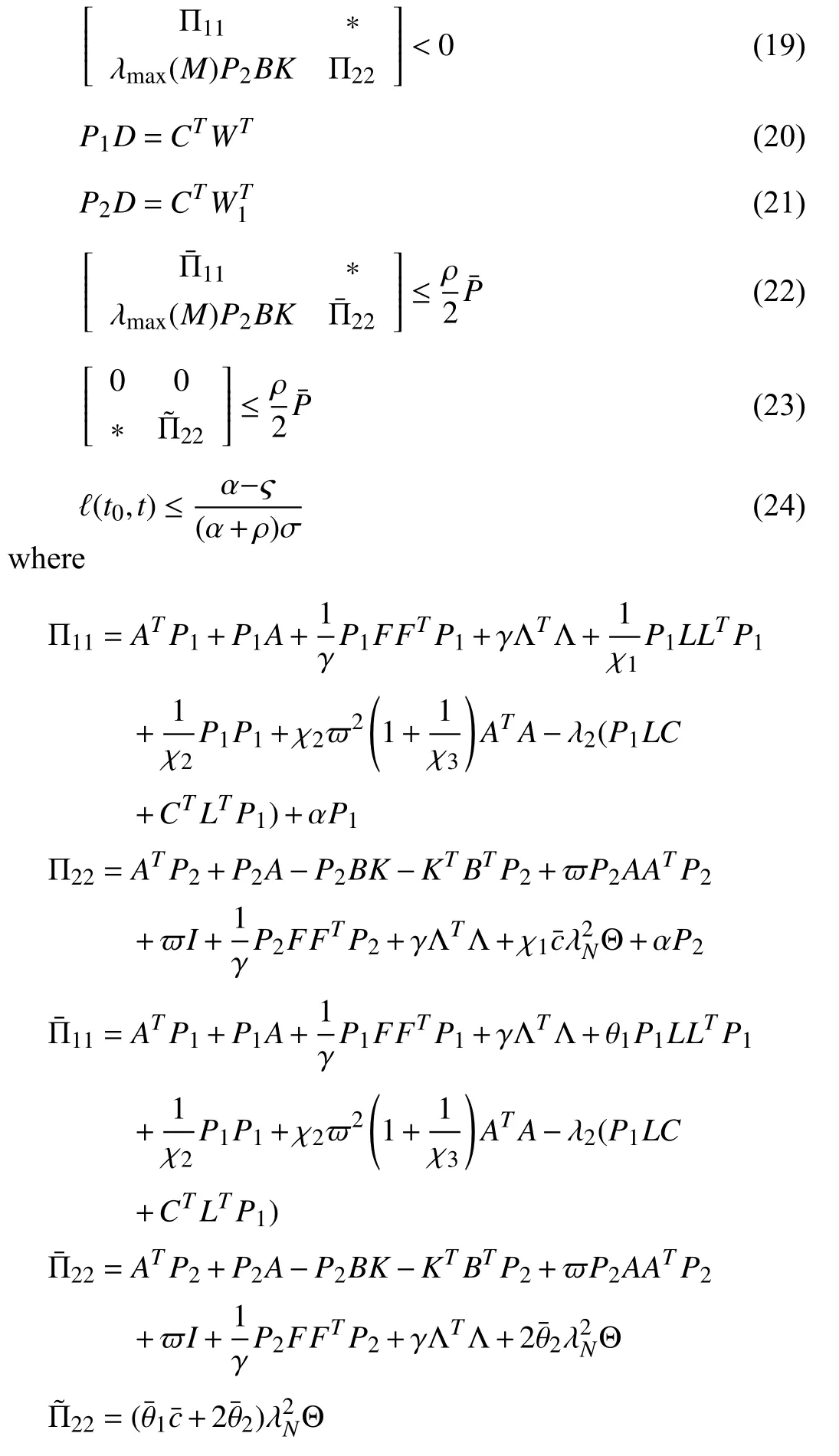

Proof:The proof of Theorem 1 is given in Appendix.■
Remark 5:In order to solve LMIs (19)–(23) more easily,we can pre-set the parameters of the same type,such as χ1,χ2,and χ3,to the same value,and then adjust them by trial-anderror method.Besides,for conditions (22) and (23) in Theorem 1,since (19)–(21) have solved forP1,P2,L,andK,we only need to find a suitableρto satisfy these conditions instead of solving forLandKwith (19)–(23).This can simplify the solution process.
Remark 6:In many existing results (such as [16],[17],[19])on the secure consensus of multi-agent systems under DoS attacks,time is divided into two parts according to whethertis during the interval of DoS attacks,so the duration and frequency of DoS attacks are restricted.However,in this paper,we discuss whether the trigger time is during DoS attacks,so there is no need to limit the frequency and duration of DoS attacks separately.Instead,we just limit the frequency of communication failures,which will also indirectly limit DoS attacks.Moreover,the constraints need to be met for all agents.
Remark 7:In previous works [16]–[19],[32],[43],algebraic Riccati equation (ARE) and algebraic Riccati inequality (ARI)are used to solve for the control gain.It should be pointed out that these methods are very conservative when the matrix dimension is large or there are many parameters.In this paper,the observer and the controller are simultaneously designed based on the LMI technique without adjusting the parameters and the symmetric positive definite matrices in advance.In addition,the obtained conditions without involving the Kronecker product will be convenient to solve.
C.Joint Design of Observer and Controller
The conditions of Theorem 1 ensure that the MAS achieves consensus and observers observe the system state under external disturbances and DoS attacks.However,sinceLandKin (19) are coupled with unknown matrices,and (20),(21)are equality constraints,they cannot be solved directly using the LMI toolbox in MATLAB.To facilitate finding a solution,the following theorem presents a design method for observer and controller gains.
Theorem 2:For given positive scalarsα,γ,χ1,χ2,χ3,νandϖ,if there exist symmetric positive definite matricesP1andP2,and matricesQ1,N,WandW1satisfying the following conditions:
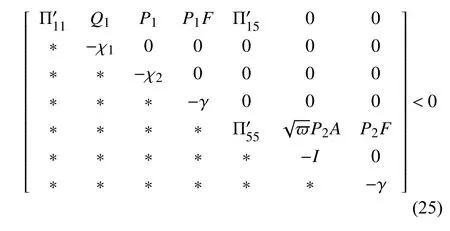

Next,using the Schur complement lemma and Lemma 2,we can obtain (25)–(28).■
D.Zeno Behavior Analysis
Zeno behavior is a very important issue in the eventtriggering strategy.Zeno behavior will result in unlimited triggers in finite time,which is physically unrealizable and obviously violates the original intention of the eventtriggering strategy to reduce the number of triggers.Therefore,we should endeavor to avoid it.
In this paper,a mixed event-triggering method is adopted to determine the triggered time instants.If DoS attacks occur,a fixed timeσis used to determine the next triggered instant,so Zeno behavior will not occur during this period.If DoS attacks do not occur,the trigger functiongi(t) in (7) will determine the next trigger moment.Next,the following theorem shows that a positive lower bound exists between two arbitrary consecutive event instants in communication areas,which proves that Zeno behavior does not occur.
Theorem 3:Under the event triggering strategy (9),Zeno behavior will not be exhibited in MAS (1) and the minimum time interval between any inter-event instants is strictly positive when DoS attacks do not occur.That is


Remark 8:It should be pointed out that the proof process of Theorem 3 is enlightened by [43].Note that the interval ϵibetween two events is related toci(t),so it is very important to select an appropriateci(t) to achieve a balance between the performance and communication burden.In addition,the existence of a hybrid update mechanism means that a lower bound always exists when DoS attacks occur;thus,this mechanism prevents continuous triggering.
IV.SIMULATION ExAMPLES
In this section,we demonstrate the validity of our method by using the communication topology shown in Fig.2.Consider each agent with the dynamic as (1) and system matrices as follows:

Fig.2.Communication topology.
In addition,the nonlinear functionf(xi(t),t) is denoted asf(xi(t),t)=[0,0,0,0.01sin(xi1(t))]T.Then,according to Assumption 3,one has Λ=diag{0.01,...,0.01}.Moreover,from Fig.2,it is easy to obtain the Laplacian matrix L whose minimum non-zero eigenvalue and maximum eigenvalue are 0.6972 and 4.3028,respectively.
It is worth noting that in the following simulation part,we consider the following two different types of disturbances acting on the first agent to show the validity of the proposed method
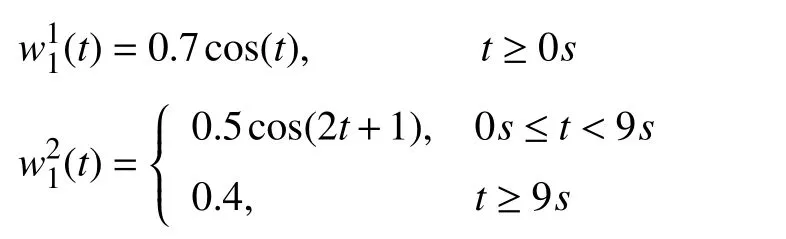
and there are no disturbances to other agents.
Then,based on Theorems 1 and 2,we choose parameters ϖ=0.0001, γ=1,χ1=0.01, χ2=4.5, χ3=0.01,ν=0.001,α=0.25,ρ=4,ς=0.001 and σ=0.04.By solving LMIs(25)–(28),the observer gainL,the controller gainKand matricesP1,W,andW1are obtained as follows:

To achieve a trade-off between the system performance and communication burden,the parameters and initial coupling gains in the trigger function (7) and the adaptive law (8) are selected asm=3, ε1=0.8, ε2=0.15, ε3=0.05, βi=0.1,c1(0)=0.27,c2(0)=0.28,c3(0)=0.28,c4(0)=0.1 andc5(0)=0.2.Furthermore,the initial states of each agent are given in Table I.
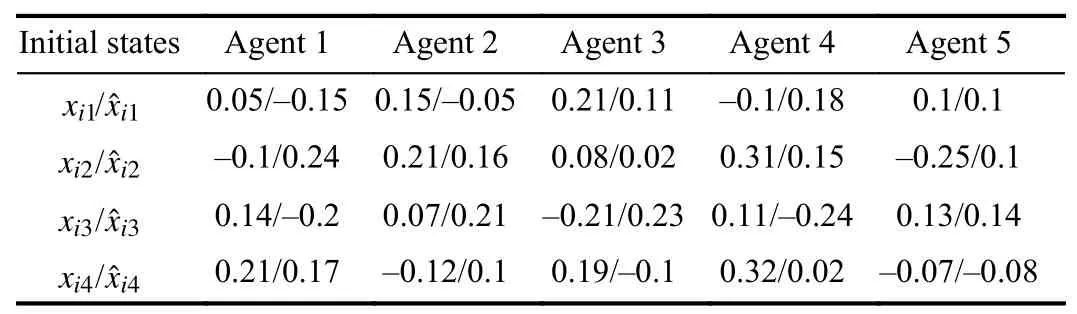
TABLEI INITIAL STATES OF EACH AGENT
It is assumed that the disturbance signaloccurs for the first agent.Define the consensus error of the whole system asThe simulation results are shown in Figs.3–7.Fig.3 displays the state trajectories of the five agents,with gray bars indicating DoS attacks that act on all agents when the attacks occur.Note that our proposed control scheme can achieve better consensus even in the presence of external disturbances and DoS attacks.The adaptive coupling gainsci(t) and triggering instants of each agent are depicted in Figs.4 and 5,respectively.From Fig.5 and through calculation,we can find that the communication failure frequency of each agent satisfies (24) and prevents Zeno behavior.In addition,we find that the dense period of trigger points corresponds to the time when the disturbance signal changes most violently,i.e.,when its first derivative is the largest.To achieve the ideal performance in the presence of disturbances,more packets are needed to adapt to the disturbances.This requires the event-triggered mechanism to generate more trigger points during the disturbance,which is consistent with the theoretical analysis.The observer errors for the first agent with or without disturbance compensationGi(t)in observer (12) underare shown in Figs.6.From this,we can see that the observer errors gradually tend toward 0 withGi(t).The consensus errors of the five agents with and without disturbance compensationzi(t) in control scheme (15)are shown in Fig.7.It can be found from Figs.6 and 7 that better state estimation performance and consensus performance are achieved by introducing disturbance compensationGi(t) andzi(t),which illustrates the validity of the proposed method.

Fig.3.State trajectories of five agents under DoS attacks and

Fig.4.Adaptive coupling gains ci(t) under

Fig.5.Triggering i nstants of each age nt under

Fig.6.Observer errors for the first agent with (a) and without (b)disturbance compensation Gi(t) in observer (12) under
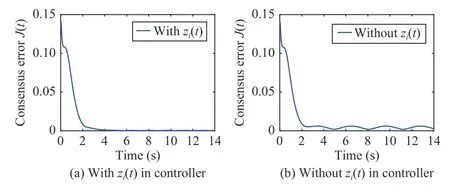
Fig.7.The consensus error of five agents with (a) and without (b)disturbance compensation zi(t) in control scheme (15) under
To further highlight the advantages of our design method,comparisons with existing methods are made in the following.To make the comparisons more obvious,suppose that the disturbance signaloccurs for the first agent,and the initial states are reset asx1(0)=[−0.05 −0.05 −0.05−0.05]T,x2(0)=[0.05 0.05 0.05 0.05]T,x3(0)=[0.1 0.1 0.1 0.1]T,x4(0)=[0.15 0.15 0.15 0.15]T,x5(0)=[0.2 0.2 0.2 0.2]T.Fig.8 displays the comparison between two different methods,one of which uses the AMETM (7) and the observer-based controller (15) proposed in this paper.The other uses the method of [44].From Fig.8,we can see that the control strategy of [44] can not achieve consensus due to the existence of external disturbances,and the designed observer can not track the states accurately.Nevertheless,our method introduces a compensation mechanism for the observer and controller,which can achieve better performance.Moreover,Table II shows the number of releases under these two different control schemes.By comparison,we can conclude that better consensus performance and state estimation performance are obtained by using the method of this paper.Furthermore,the communication burden is also reduced.
V.CONCLUSIONS

Fig.8.Comparison between proposed observer-based control scheme (15)in Theorem 1 and the method in [44] under

TABLEII TRIGGER NUMBERS OF EACH AGENT UNDER DIFFERENT CONTROL SCHEMES
In this paper,the consensus problem of nonlinear MASs subject to DoS attacks is studied.More practically,external disturbances and uncertainties have also been considered in this work.An observer-based controller design method is proposed to ensure the consensus of MAS under DoS attacks and disturbance signals.The controller gain and observer gain are obtained through a joint design method.Moreover,to reduce the communication burden,an AMETM for MAS is designed,whose updates not only depend on the current state but also previously stored information,and Zeno behavior is eliminated.Finally,simulation results show the advantages of our method.Note that in this paper,only undirected network communication is considered in the cyber layer.Thus,how to extend this result to directed network communication is an interesting future research direction.In addition,extending these results to fault-tolerant problems will also be a future research topic.
APPENDIx
Proof of Theorem 1:Choose the Lyapunov function candidate as follows
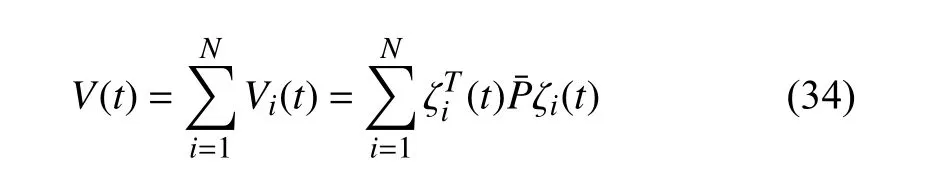
where ζi(t)=col{exi(t),δi(t)}.Then,according to whetheris under attack instant,we divide the proof process into two parts.First,consider


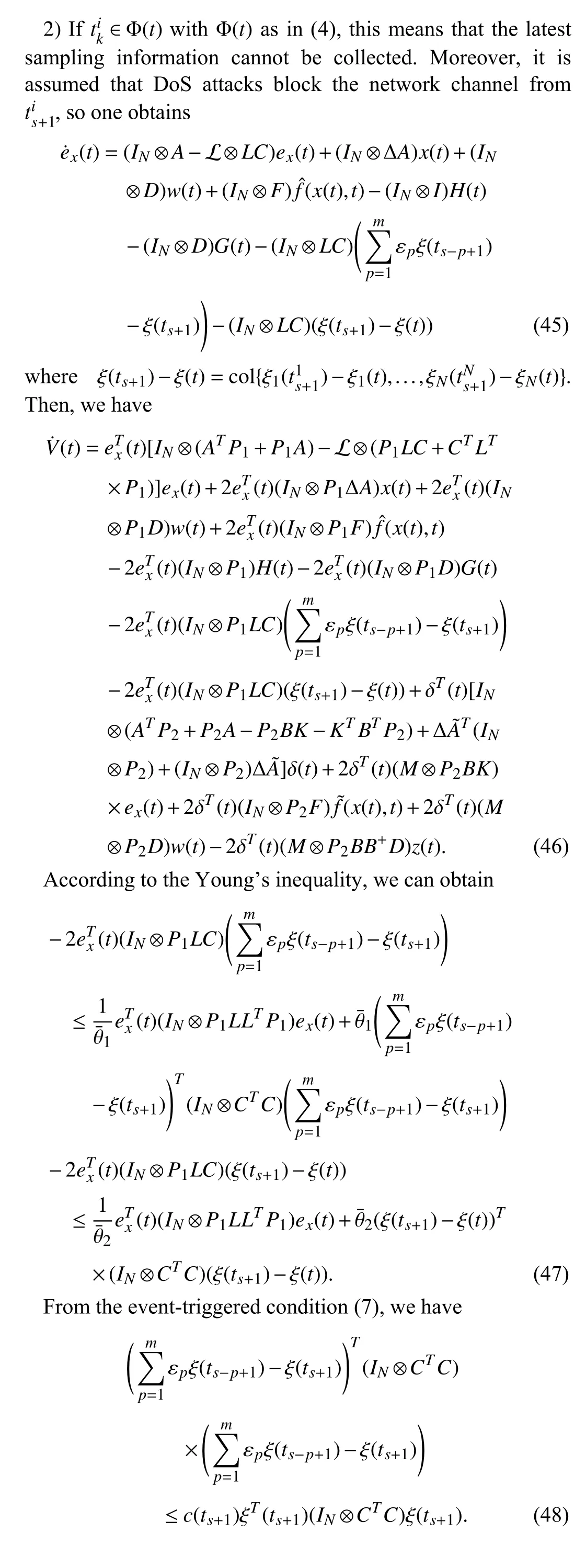
Additionally,it is easy to conclude that
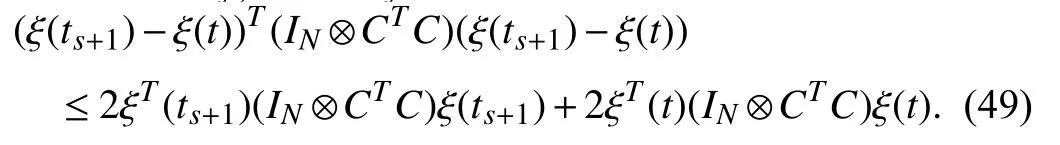
Next,using the analysis methods in Part 1),combining (47)and (48) with (49),and according to LMIs (22) and (23),we can deduce from (46) that

which means thatV(t) is bounded.Therefore,the secure average consensus of MASs (1) is guaranteed.■
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Limited-Budget Consensus Design and Analysis for Multiagent Systems With Switching Topologies and Intermittent Communications
- Reduced-Order Observer-Based Leader-Following Formation Control for Discrete-Time Linear Multi-Agent Systems
- Distributed Order-Up-To Inventory Control in Networked Supply Systems With Delay
- Variational Gridded Graph Convolution Network for Node Classification
- Hierarchical Reinforcement Learning With Automatic Sub-Goal Identification
- Theory and Experiments on Enclosing Control of Multi-Agent Systems
