Command Filtered Finite/Fixed-time Heading Tracking Control of Surface Vehicles

Zhenyu Gao and Ge Guo,

Abstract—This paper investigates the heading tracking problem of surface vehicles with unknown model parameters.Based on finite/fixed-time control theories and in the context of command filtered control,two novel adaptive control laws are developed by which the vehicle can track the desired heading within settling time with all signals of the closed-loop system are uniformly bounded.The effectiveness and performance of the schemes are demonstrated by simulations and comparison studies.

I.INTRODUCTION

RECENTLY,the heading tracking problem for surface vehicles has received much interest,owing to it is directly related to the operation,economy,safety,and effectiveness of the vehicle control system.To track the desired heading,a proportional-integral-derivative (PID) controller,which greatly improves steering performance,was presented in 1920s.Later,many advanced control algorithms,such as modern optimal control [1],neural network control [2]–[4],robust control [5],[6],and fuzzy control [7],have been applied to heading control of surface vehicles.However,the control approaches in [1]–[7] can only obtain the infinite-time stability of tracking systems,where it is generally known that the finite-time stability is more practical than the infinite-time stability in a real control system.

To handle the finite-time control of the system,many interesting results have been obtained in recent years [8]–[11].These research works are based on the theory of finite-time stability or fixed-time stability [12].In addition,the system with finite-time or fixed-time convergence usually demonstrates not only faster convergence rates,but also has better rejection features against uncertainties and disturbances.Although the idea of finite-time and fixed-time control are promising,research works so far has been solely focused on stabilization of various nonlinear system [9]–[11] and the consensus of multi-agent systems [13],[14].Here,we aim to extend the control strategies under finite/fixed-time control frameworks such that the heading tracking can be achieved with faster convergence rates and higher tracking precision.

It is also worth mentioning that,the results mentioned above are all based on backstepping methods.As we all know,the backstepping method is subject to the problem of“explosion of complexity”caused by repeated differentiations of the virtual control signals.To eliminate this defect,the adaptive dynamic surface control method [15] was applied to address heading tracking control in [16],[17].However,since command filters are used to deal with differentiation of the virtual control signals,the control performance of this method may be affected by the filtering errors.Recently,[10],[18],[19] gave a new command-filtered control method to remove the filtering errors by introducing a compensator for each control signals.However,the filtering errors cannot be eliminated within setting time.

Motivated by the aforementioned observations,this paper aims to give two novel adaptive control schemes,by which the desired heading can be tracked within a given settling time.The main contributions are summarized as follows:

1) Proposing a finite-time and a fixed-time backstepping control scheme with which the vehicle can track the given heading with all the signals uniformly bounded and the tracking errors converge to a neighborhood of zeros within the settling time.Besides,under the proposed finite/fixed-time control scheme,the system has better robustness to external disturbance and uncertainty.

2) Incorporating the compensator-based command filter technique into the proposed control scheme,by which the issue of“explosion of complexity”is eliminated,the filtering error can be compensated within finite/fixed time and the controller design procedure is much simpler and easier for implementation.

This paper is organized as follows.Section II contains the preliminaries and problem statement.Section III presents the controller design and stability analysis.Section IV gives the simulation studies.Finally,some conclusions are drawn in Section V.

II.PRELIMINARIES AND PROBLEM STATEMENT

A.Preliminaries

B.Problem Statement

Consider the following Norrbin nonlinear model describing the steering dynamics of a surface vehicle,depicted by [17]

where ψ ∈R is the course angle,δ ∈R is the actual rudder angle,T∈R is the time constant,K∈R is the gain constant,and γ ∈R is the Norrbin coefficient.

For simplicity,the model (10) can be transformed into the following state space expression:

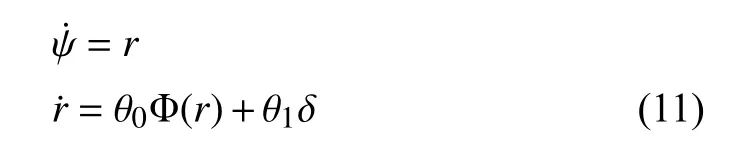
whereris the yaw velocity of the vehicle,and θi,i=0,1,are model parameters.

To facilitate the control design,the following assumption is made.

Assumption 1:The parameters θi,i=0,1,in (11) are unknown yet bounded.

Remark 1:Since the model parametersK,T,and γ are susceptible to external factors,such as velocity,shape,and load of vehicles,depth of water,etc,they are difficult to obtain accurately,but they are bounded.Hence,the Assumption 1 is reasonable.

The objective of this paper is to design two control schemes(i.e.,a finite-time and a fixed-time control scheme) for a surface vehicle with unknown model parameters,so that the actual heading ψ tracks the desired heading ψdwithin the settling time successfully as shown in Fig.1,while guaranteeing all signals of the closed-loop system are uniformly bounded.Further,the control objective can be stated mathematically as

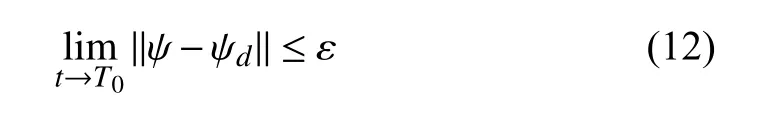
Fig.1.Heading tracking of a surface vehicle.

Fig.2.Schematic of heading tracking control of a surface vehicle.

and

whereT0,ε are positive constants,andT0∈[0,∞).

III.CONTROLLER DESIGN AND STABILITY ANALYSIS

In this section,two adaptive control schemes combining the adaptive technique with the command filter-backstepping design procedure,as shown in Fig.2,will be given.

Define the heading tracking errorz1and yaw angle velocity tracking errorz2as follows:

A.Adaptive Finite-time Controller Design

In this subsection,a finite-time control scheme is proposed,and the controller design contains the following two steps.

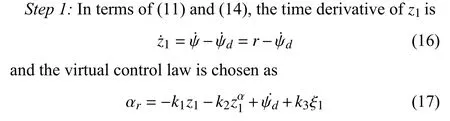
whereki,i=1,2,3,and α are positive gain constants withk1>k3/2,0<α<1,and ξ1is a compensating signal which will be given later.

To generate the stabilizing functionand it is derivativethe nominal stabilizing function is then passed through the following finite-time command filter

where λ1and λ2are positive constants,φ1,1is the estimate of αr,ι is the derivative of φ1,1,φ1,1(0)=αr(0) and ι(0)=0.

Remark 2:If λ1and λ2are properly chosen,then we haveafter a finite time of transient process and the corresponding solutions of the dynamic systems are finite time stable in the absence of input noises.

In practice,the input noise is inevitable,and to compensate for the filtering error,defines the filtering errorand then the compensating signal is defined as

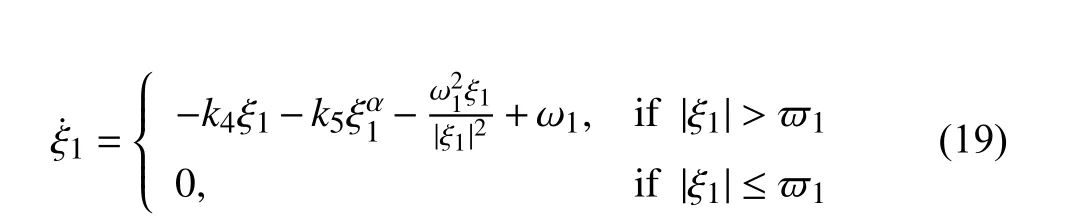
where ϖ1,k4,k5are positive constants withk4>(k3+1)/2 and ξ1(0)=0.

Remark 3:Compared with the compensator-based command filter technique in [10],[18],[19],the proposed command filter technique (18) and (19) can not only eliminated the problem of“explosion of complexity”,but also can compensate the filtering error within finite time.

Here,the candidate Lyapunov function is selected as

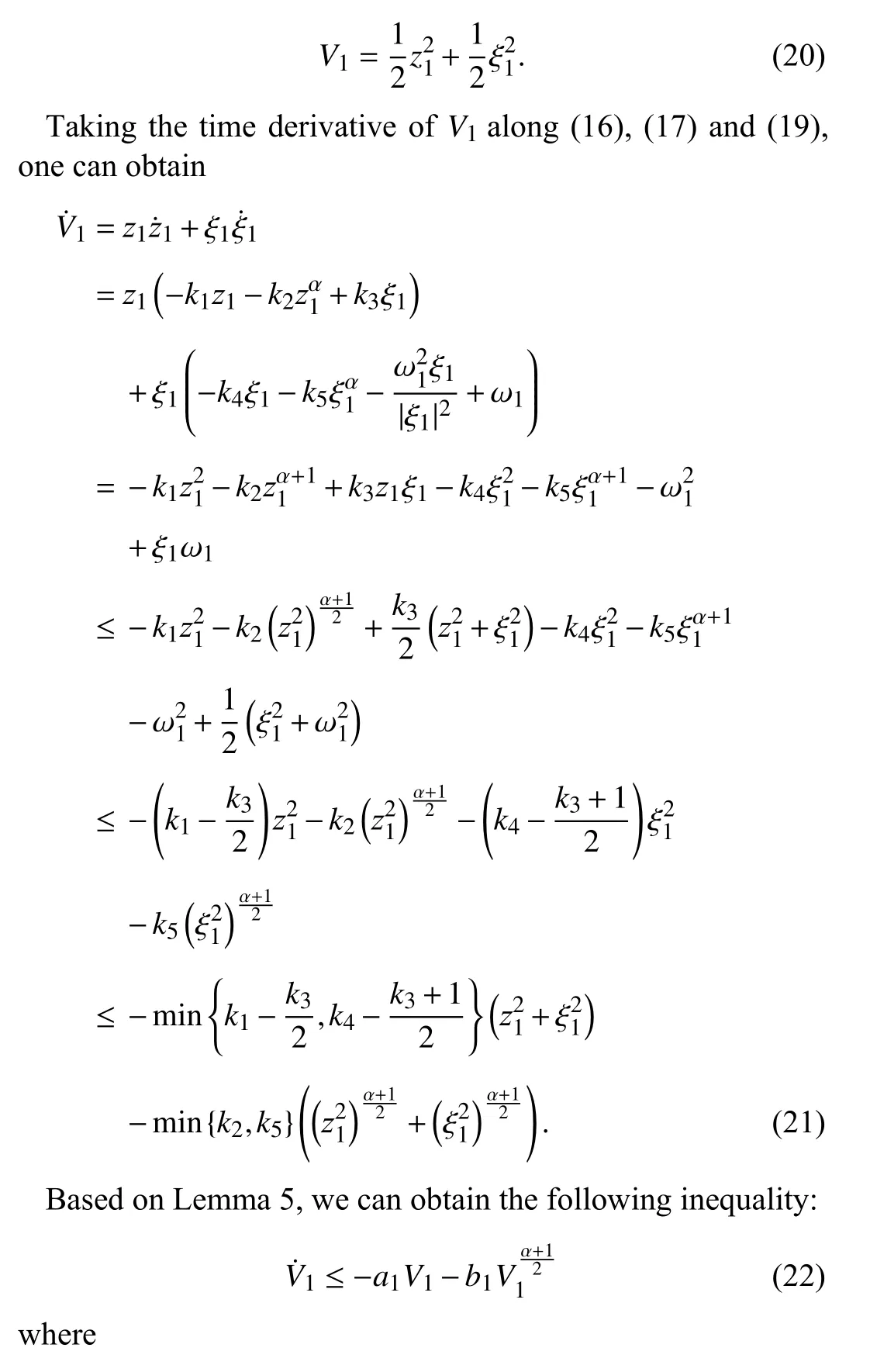
According to Lemma 2,it can be concluded that the systemz2is practically finite-time stable.

Consider the following candidate Lyapunov function for the whole system

Therefore,there is the following theorem.

Theorem 1:Consider the nonlinear heading dynamics of surface vehicles in (11) under Assumption 1,the heading tracking can be achieved by the proposed actual input (24)with virtual input (17),command filter (18),the compensating signal (19) and adaptive laws (25),(26),while guarantee that all signals of the closed-loop system are uniformly bounded and all tracking errors will convergence to a region near neighborhood of zeros in finite time.

Proof:Based on (31) and Lemma 5,one can obtain

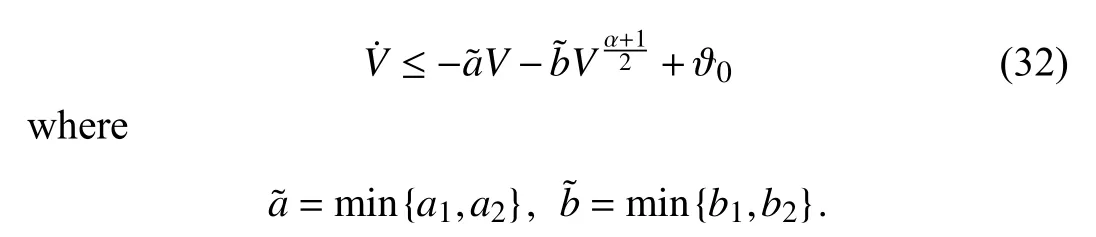
According to Lemma 2,it is easy to obtain that the system is practically finite-time stable,and the residual set of the system(30) is given by

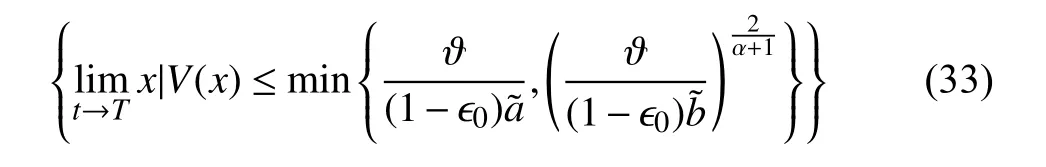
Remark 4:Although the proposed control scheme above can ensure that the desired heading can be tracked in finite time,the convergence time cannot be determined beforehand,since it depends on the initial states of the system which is usually unknown.

With the above finite-time control scheme,the convergence time depends on the initial states of the system and the heading tracking objective cannot be achieved within a given time.Therefore,in the next subsection,we will give a fixedtime control scheme.

B.Adaptive Fixed-time Controller Design

Here,a fixed-time control scheme is developed for the heading tracking of surface vehicles.

Step 1:Here,the virtual input is chosen as follows:

where φ2,1is the estimated value of αr,ι1,1is the derivative of φ2,1, λ1,i,i=1,2,3,4,are positive constants,andm1,1=α,n

1,1=β,m1,2=α/(2−α),n1,2=2β−1, φ2,1(0)=αr(0),and ι1,1(0)=0.

Remark 5:For the command filter (36),if the parameters λ1,1, λ1,2,λ1,3,and λ1,4are properly chosen,the following equalities φ2,1=αr,andare true in the absence of input noises after a fixed time of transient process,and the corresponding solutions of the dynamic systems are fixedtime stable.

Here,the compensating signal is generated by the following system:

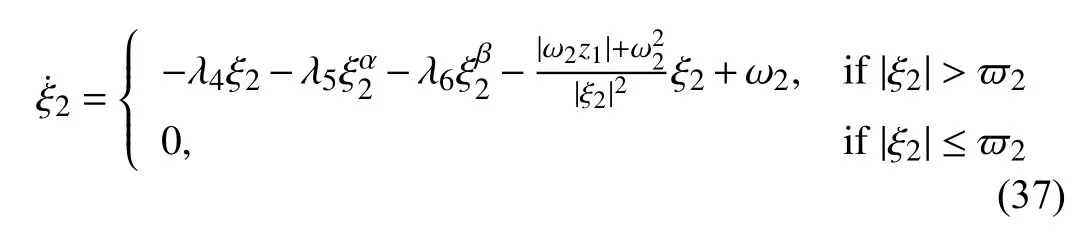
where ϖ2and λi,i=4,5,6,are positive constants with

Remark 6:Compared with the compensator-based command filter technique in [10],[18],[19] and the command filter technique (18) and (19),the proposed filter (36) and (37)can avert repeated differentiations of the virtual control signals which reduced the computation greatly.Meanwhile,the filter proposed here can compensate the filtering error within fixed time.

Here,consider the same Lyapunov function as (20),and taking the time derivative ofV1along (35) and (37),one can obtain

Therefore,there is the following theorem.

Theorem 2:Consider the nonlinear heading dynamics of surface vehicles in (11) under Assumption 1,the heading tracking can be achieved by the proposed actual input (40)with virtual input (35),command filter (36),the compensating signal (37),and adaptive laws (41),(42),while guaranteeing all signals of the closed-loop system are bounded and all tracking errors converge to a neighborhood of zeros within the settling time regardless of the initial states of the system.

Proof:In view of (45),one can easy obtain

Remark 7:According to (48),we can see the maximum convergence time only depends on the controller parameters and ϵ1.Therefore,the presented method allows one to arbitrarily choose the convergence rate of the heading tracking control of surface vehicles,which makes it feasible for us to meet strict settling time requirements in practical applications.Moreover,the fixed-time algorithm can ensure a fixed settling time regardless of the initial states of surface vehicles.

Remark 8:By selecting the controller parametersand ϵ to satisfy corresponding constraints as mentioned in the above discussions,we can guarantee a bound of the settling time as given in (48),which determines a certain convergence rate.Generally,the relation between the convergence rate and these parameters are shown in Table I.

Remark 9:From the stability analysis and the definition of convergence time (48),we can see that the values of controller parameters do not affect the stability of the closed-loop system,although they may influence the convergence time.

TABLEI RELATIONSHIP BETWEEN PARAMETERS AND CONVERGENCE RATE

For a practical tracking control problem,the desired convergence time cannot be too short,otherwise,the closedloop system may be instable due to saturation constraint of the thruster.In addition,a feasible convergence time should also take the transient performance into consideration in the design procedure according to the maximum maneuver capability.

Remark 10:The Lyapunov function (20) in the paper is in general a non-quadratic,and according the result in [22] and[23],the non-quadratic Lyapunov functions usually result in better performance compared with quadratic functions.In this paper,the usage of non-quadratic Lyapunov function and finite/fixed-time theory leads to improved convergence of the system error signal to zero.

IV.SIMULATION STUDIES

In this section,we do the high-fidelity simulations using the module MSS/control/autopilots/heading autopilot model from the marine system simulator (MSS) toolbox [24] developed by the Department of Marine Technology,Norwegian University of Science and Technology,Norwegian.An autopilot with the following parametersT=21 s,K=0.23 s−1, γ=0.3 s2are taken as the simulation example.The design parameters of finite-time controller arek1=k6=2,k2=k7=5/7,k3=k4=3/2, γ1=γ2=0.1,ι0=3, ι1=5, α=5/7,and the parameters of fixed-time controller are λ1=λ7=2,λ2=λ5=λ8=5/7, λ3=λ6=λ9=3/5, λ4=2, γ3=γ4=0.1,ι2=3,ι3=3,α=5/7, β=5/3 and ϖ1=ϖ2=0.2.To show the relation between convergence time and initial states,the following initial states are chosen(ψ1(0)=0,r1(0)=0) and(ψ2(0)=−10,r2(0)=10).

In this simulation,the reference heading of the vehicle is given as

A.Performance of Proposed Heading Tracking Control Schemes

In this subsection,the simulations are carried out using the proposed control schemes.

Case 1:Adaptive finite-time (FinT) controller;

Case 2:Adaptive fixed-time (FixT) controller.

Fig.3.Desired heading and actual heading with different initial states under adaptive FinT/PID controller.

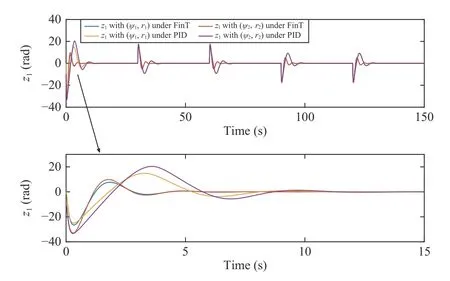
Fig.4.Heading tracking error z1.

Fig.5.Paramet er estimat es and

Simulation results are shown in Figs.3–14.The results of the heading tracking control with different initial conditions under FinT controller and PID controller are shown in Figs.3 and 4.Here,the PID controller is chosen as δPID=From these figures we can see,under the same FinT controller parameters,different initial states have different convergence time that means the settling time depend on the initial states of the system.Furthermore,the FinT controller has faster convergence speed than PID controller.Fig.5 shows the estimate result of θ0and θ1,which will converge to their true values under the proposed adaptive law.Fig.6 shows the filtering errorin FinT control scheme,by which we can see the filter with compensator has smaller filtering error.Fig.7 shows the filtering errorwith the command filter in[19] and the finite-time command filter proposed in this paper.From the result in Fig.3,it is shown that the proposed finitetime command filter not only has faster convergence rate but also achieves better tracking effect.Fig.8 shows the actual control input δ in FinT control scheme,by which the heading tracking control can be achieved.

Fig.6.Filtering err or αr −with/without compensator.

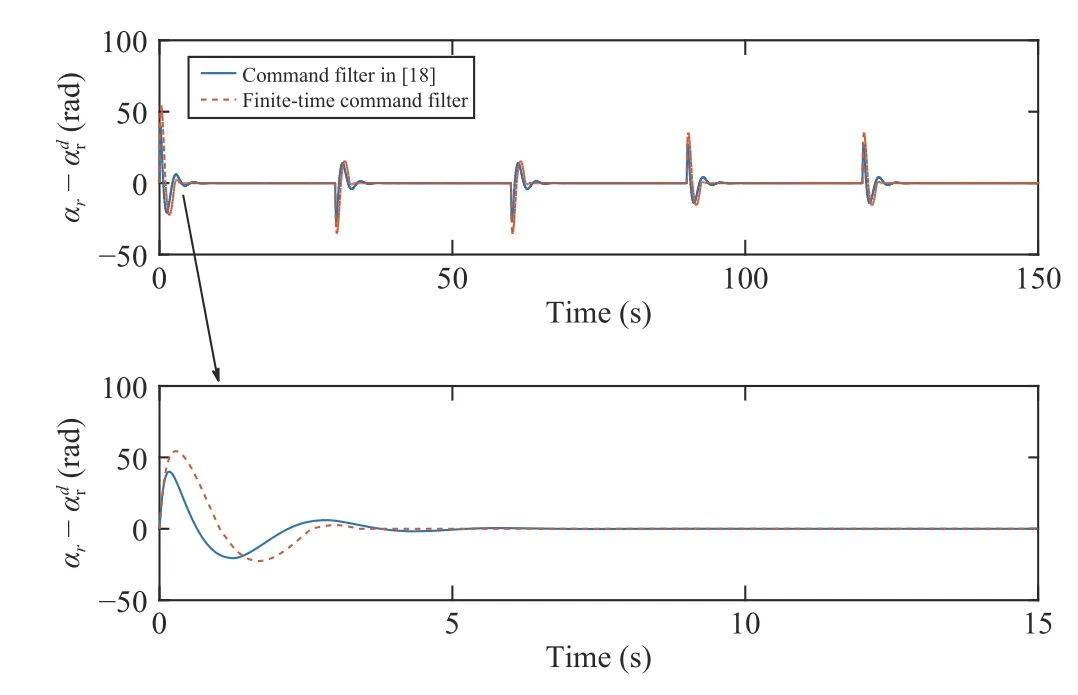
Fig.7.Filtering errorαr −with different command filter.

Fig.8.The actual control i nput δ under the FinT controller.

Fig.9.Desired heading and actual heading with different initial states under adaptive FixT/FinT controller.

Fig.10.Heading tracking error z1.

Fig.11.Para meter esti matesand

Figs.9 and 10 show the results of the heading tracking control under the proposed FixT controller and FinT controller.From these two figures we can see,with the same parameters of FixT controller,the vehicle will track the desired heading within the same settling time regardless of the initial condition.Besides,under the proposed adaptive law,the unknown parameters θ0and θ1can be estimated as shown in Fig.11.Filtering error with/without compensator is shown in Fig.12,which implies that the filter with compensator has better performance.Fig.13 shows the result of filtering errorunder the command filter in [19],the finite-time command filter,and the fixed-time command filter proposed in this paper.The simulation results indicate that the fixedtime command filter has the best performance,that is,faster tracking speed and higher tracking accuracy.Fig.14 shows the actual control input δ in FixT control scheme,by which the heading tracking control can be achieved within settling time.

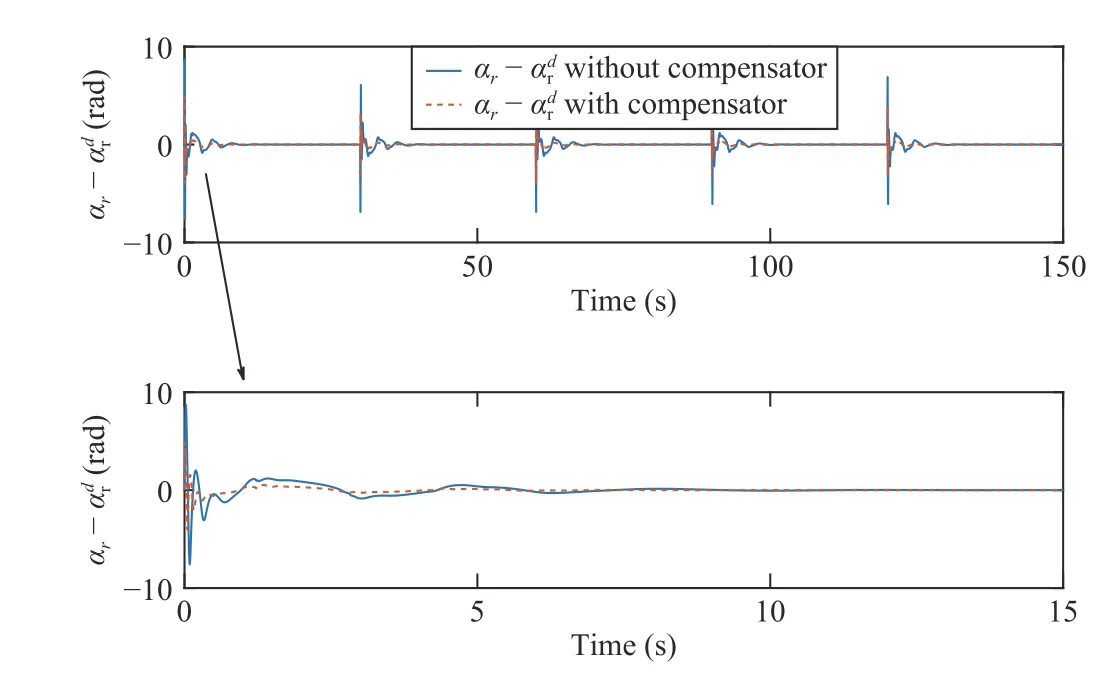
Fig.12.Filteringerror αr −with/without compensator.

Fig.13.Filtering error αr −withdifferent command filter.

Fig.14.The act ual control input δ under the FixT controller.

B.Performance of Proposed Heading Tracking Control Schemes Under Disturbance

The time-varying external disturbance is taken asd(t) with the Gaussian random process.

The simulation results are depicted in Figs.15 and 16 and the performance indices are also summarized in Table II.It is observed from Figs.15 and 16 and Table II that the proposed heading tracking control law exhibits almost identical control performance in presence of disturbance,which shows that the proposed control law has better rejection feature against disturbance.

Fig.15.Desired heading and actual heading with disturbance under adaptive FixT/FinT and PID controller.

Fig.16.Heading t racking error z1 under disturbance.

V.CONCLUSION

The paper presents two novel control schemes of heading tracking control of surface vehicles with model parameter uncertainties.Firstly,a novel finite-time control scheme is proposed by which the vehicle can tracks the desired heading in finite-time that depends on the initial states of the system.In order to solve the drawback of convergence time related to the initial states,then,a fixed-time control scheme is developed,with which the control objective can be achieved within the settling time independent of the initial conditions,while guaranteeing all signals of the closed-loop system are uniformly bounded and the tracking errors converge to a neighborhood of zeros within the settling time.In addition,to eliminate the problem of“explosion of complexity”in backstepping method,compensator-based command filter technique is introduced to obtain the derivative of virtual input.Simulation results demonstrate the effectiveness of the proposed control method.In future work,we plan to extend the finite/fixed-time control theory to trajectory tracking or formation control of surface vehicles,and investigate the possibility of heading control of surface vehicle within settling time in the presence of actuator saturation.

TABLEII PERFORMANCE COMPARISON OF THE PROPOSED CONTROL SCHEME AND PID SCHEME