Variational Gridded Graph Convolution Network for Node Classification
2021-10-25XiaobinHongTongZhangZhenCuiandJianYang
Xiaobin Hong,Tong Zhang,Zhen Cui,and Jian Yang
Abstract—The existing graph convolution methods usually suffer high computational burdens,large memory requirements,and intractable batch-processing.In this paper,we propose a high-efficient variational gridded graph convolution network(VG-GCN) to encode non-regular graph data,which overcomes all these aforementioned problems.To capture graph topology structures efficiently,in the proposed framework,we propose a hierarchically-coarsened random walk (hcr-walk) by taking advantage of the classic random walk and node/edge encapsulation.The hcr-walk greatly mitigates the problem of exponentially explosive sampling times which occur in the classic version,while preserving graph structures well.To efficiently encode local hcr-walk around one reference node,we project hcrwalk into an ordered space to form image-like grid data,which favors those conventional convolution networks.Instead of the direct 2-D convolution filtering,a variational convolution block(VCB) is designed to model the distribution of the randomsampling hcr-walk inspired by the well-formulated variational inference.We experimentally validate the efficiency and effectiveness of our proposed VG-GCN,which has high computation speed,and the comparable or even better performance when compared with baseline GCNs.
I.INTRODUCTION
IN recent years,convolutional neural networks (CNNs) [1]have achieved great success in a variety of machine learning tasks such as object detection [2],[3],machine translation [4],and speech recognition [5].Basically,CNNs aim to explore the local correlation through neighborhood convolution,and are rather sophisticated to encode Euclidean structure data w.r.t.shape-gridded images and videos.In realworld applications,however,there is a large amount of non-Euclidean structure data such as social networks [6],citation networks [7],knowledge graphs [8],protein-protein interaction [9],and time series system [10]–[14],which are usual non-grid data and cannot be habitually encoded with the conventional convolution.
As graphs are natural and frequently-used to describe nongrid data,researchers have recently attempted to introduce convolution filtering into graph modeling,which is called graph convolution or graph convolution network (GCN).Generally,they fall into two categories:spectral based approaches [15]–[22] and spatial based approaches [23]–[26].
Spectral based approaches employ the recent emerging spectral graph theory to filter signals in the frequency domain of graph topology.Brunaet al.[15] proposed the first spectral convolution neural network (Spectral CNN),which defines the filter as a set of learnable parameters to process graph signals.Chebyshev Spectral CNN (ChebNet) [16] defines the Chebyshev polynomial of eigenvector diagonal as the convolutional filter,which avoids the computation of the graph Fourier basis,reducing the computation complexity from O(N3) to O(Ke) (whereNis the number of nodes,eis the number of edges,andKis the number of engine vectors).Kipf and Welling [17] proposed the most commonly used GCN,which is essentially a first-order approximation of ChebNet assumingK=1 and the max-eigenvalue λmax=2.Wuet al.[22] proposes a disordered graph convolutional neural network (DGCNN) based on the Gaussian Mixture Model,which extends CNN by adding a preprocessing layer called disordered graph convolutional layer (DGCL).DGCL uses a mixture of Gaussian functions to achieve the mapping between the convolution kernel and nearby nodes in the graph.Besides,some other GCN variants have also been proposed,including Hessian GCN (HesGCN) [19] and Hypergraph p-Laplacian GCN (HpLapGCN) [20].Specifically,HesGCN and HpLapGCN belong to the first-order variant of GCN,while TGCN [21] is the second-order approximation of GCN.
These spectral based methods above are well-supported by the strong theory of graph signals,but they usually suffer high computational burdens because of the eigenvalue decomposition on graph topology.To mitigate this problem,the fast approximation algorithm [27]–[29] defines convolution filtering as a recursive calculation on graph topology,which actually may belong to the category of spatial convolution.
Spatial based approaches often use explicitly spatial edgeconnection relations to aggregate those nodes locally adjacent to one reference node.The local aggregation with mean/sum/max operation on neighbor nodes cannot yet satisfy the Weisfeiler-Lehman (WL) test [30],where non-isomorphism graph structures need different filtering responses.The critical reason is that graph topology structures are degraded to certain-degree confusion after aggregation,even though the recent graph attention networks (GAT) [31] attempts to adaptively/discriminatively aggregate local neighbor nodes with different weights learnt by the attention mechanism between one central node and its neighbor nodes.Moreover,spatial based GCNs usually need to optimize the entire graph during training due to the intractability of batch-processing,which will result in high-memory requirements for large-scale graphs and thus cannot run on plain platforms.This means that,when graph structures change with newly-added/deleted nodes or links,the GCN models should be well-restarted or even re-trained for new structures.In addition,the time complexity of spatial based GCNs will be exponentially increased with the receptive field size (w.r.t.the hop stepl),i.e.,O(Nmld2) in each convolution layer,wheremdenotes average degree of nodes,anddis the dimension of input signal.
In this paper,we propose a high-efficient variational gridded graph convolution network (VG-GCN) with highcomputation efficiency,low-memory cost,easy batch-process,and comparable or even better performance when compared with the baseline GCNs.To efficiently capture local structures,we introduce the random sampling strategy through random walks,which can well preserve graph topology under randomly sampling sufficient walks [32],[33].As the quantity of walks has the exponentially-explosive increase with the walk step,i.e.,O(Nml),the burden of sampling sufficient walks tends to overwhelm the entire algorithm especially for the larger node degreem≫2.Instead of the original random walk,specifically,we propose a hierarchically-coarsened random walk (hcr-walk) to reduce sampling times.The strategy of hcr-walk can efficiently reduce traversal edges through random combinations (to form hyper-edge) of connection edges during walking.As a result,the hcr-walk balances the advantages of random walk as well as node aggregation.Under the fixed hyper-edge numberthe hcrwalk will fall into a deep-first traversal onwhose height may be limited in the radius of graph to cover the global receptive field.In view of the limited height,as well as the smallvalue,a small amount of sampling times could well preserve most information of topology structures as well as node signals.
To efficiently encode the local hcr-walk around each reference node,we project the hcr-walk onto an ordered space to form image-like grid-shape data,which better favors those conventional convolution networks.Thus,a 2-D convolution filtering can be performed in the normalized hcr-walk space to encode the correlation of within-walk adjacencies and cross adjacent walks.To characterize the uncertainty of latent feature representation,we design a 2-D variational convolution block (VCB) inspired by the recent variational inference,rather than directly adopting 2-D convolution filtering.The benefit of variational convolution is that the probability distribution of random sampled walks could be well modeled and the performance could be further boosted.The proposed hcr-walk can be framed in an end-to-end neural network with high running speed even on large-scale graphs.
Our contributions are three-fold:
1) We propose the hcr-walk to describe local topology structures of graphs,which can efficiently mitigate the problem of exponentially-explosive sampling times occurring in the original random walk.
2) We project the hcr-walk onto the grid-shape space and then introduce 2-D variational convolution to describe the uncertainty of latent features,which makes the convolution operation on graphs more efficient and flexible,just as the standard convolution on images,and well support batchprocessing.
3) We experimentally validate the efficiency and effectiveness of our proposed VG-GCN,which has a high-efficient computation speed,and comparable or even better performance when compared with those baseline GCNs.
II.RELATED WORk
In this section,we will introduce previous literatures which are related to our work.Generally,they can be divided into three parts:graph convolutional neural networks,random walk,and variational inference.
A.Graph Convolutional Neural Networks
With the rapid development of deep learning,more and more graph convolutional neural network models [34]–[37]are proposed to deal with the irregular data structure of graphs.Compared with regular convolutional neural networks on structured data,this is a challenge since each node’s neighborhood size varies in graphs,while the regular convolutional operation requires fixed local neighborhood.To address this problem,the graph convolutional neural networks fall into two categories,spectral-based convolution and spatial-based convolution.Spectral-based filtering method was first proposed by Brunaet al.[15].It defines the filter operators in spectral domain,and then implements a series of convolution operations through the Laplace decomposition of graphs.Because the spectrum filter includes the process of matrix eigenvalue decomposition,the computational complexity is generally high,especially for graphs with a large number of nodes.To alleviate the computation burden,Defferrardet al.[16] proposed a local spectral filtering method,which approximates the frequency responses with the Chebyshev polynomial.Spatial-based filtering methods simulate the image processing approach of regular convolutional neural networks,and employ convolution based on nodes’ spatial relations.The general approach of spatial convolution is to construct the regular neighborhood of nodes through sampling (discarding a part of nodes if the neighbor number exceeds while repeating a part of nodes if the neighbor number is insufficient),and then carry out the convolution operation with the convolution kernel of rules.According to whether the data to be predicted can be known from the model in training stages,it can be divided into transductive learning [38] and inductive learning [39].Specifically,for the inductive learning,the data to be predicted is not accessible during training,and the data of the model may be in an“open world”.
B.Graph Clustering
Graph clustering aims to depart a complete graph G toKdisjoint subsets V1,...,VK.The vertices within clusters are densely connected,while the vertices in different clusters are sparsely connected.Graph clustering plays an important role in community detection [40]–[42],telecommunication networks [43],and email analysis [44].Heet al.[45] proposed a dubbed contextual correlation preserving multiview featured graph clustering (CCPMVFGC) for discovering clusters in graphs with multiview vertex features.To address the problem of identifying clusters in attributed graphs,Huet al.[46] proposed an inductive clustering algorithm (MICAG) for attributed graphs from an alternative view.To overcome the problem where common clustering models are only applicable to complex networks where the attribute information is composed of attributes in binary form,Huet al.[47] proposed a three-layer node-attribute-value hierarchical structure to describe the attribute information in a flexible and interpretable manner.
C.Random Walk
Random walk is an effective method to get graph embedding.It is especially useful in the situation that the graph is partially visible or the graph is too large to measure in its entirety.Given a graph composed of nodes and the connection between nodes,walk paths can be obtained by selecting the start nodes and then executing random walk with certain sampling strategies.The commonly used random walk strategies generally include the truncated random walk[48]–[50] and the second-order random walk [51].Analogous to tasks in natural language processing where all the nodes in a graph constitute a dictionary,a walk path is regarded as a sentence,and a node in the path is regarded as a word.Graph embedding can be learned by adopting the continuous bag-ofwords (CBOW) model [52] or the Skip-gram model [53].Specifically,the CBOW model uses context to predict the central node embedding,while the Skip-gram model predicts the context nodes based on the central node embedding.Among them,Skip-gram model is the most widely used one.Skip-gram aims to maximize the co-occurrence probability among the words that appear within a windoww.Among various graph embedding methods based on random walk,DeepWalk and node2vec are two typical examples.
1) DeepWalk:DeepWalk preserves the high-order proximity between nodes by maximizing the co-occurrence probability of the lastknodes and nextknodes in the path centered at vertexvi:maximizing logPr(vi−k,...,vi−1,vi+1,...,vi+k|Yi),where 2k+1 is the walk length.It produces lots of walks and optimizes the logarithmic probability of all paths.
2) node2vec:node2vec controls the partial random walk on the graph by two hyper-parameterspandq,which can be seen as providing a trade-off between breadth-first (BFS) and depth-first (DFS) graph searching,and hence produces higherquality and more informative embedding than DeepWalk.
D.Variational Inference
Variational inference is a fast and effective method from machine learning that approximates probability densities for a large amount of data.In Bayesian statics,the inference of unknown quantities can be regarded as the calculation of posterior probability,which is usually difficult to calculate.The usual approach is to make an approximation using the Markov Chain Monte Carlo (MCMC) algorithm [54],which is slow for large amounts of data due to the sampling.Different from MCMC,the idea behind variational inference is to first posit a family of densities based on latent variables,and then to find the member of that family which is close to the target.Specifically,the degree of closeness is usually described by the Kullback-Leibler (KL) divergence.Moreover,Kingma and Welling [55] proposed the reparameterization trick to solve the non-differentiable problem in optimization caused by the sampling of the involved latent variables.
III.VG-GCN
In this section,we will introduce our VG-GCN in detail.We first define the notations used in this paper and overview the entire architecture of VG-GCN,then introduce the main modules of VG-GCN,including hcr-walk,gridding,and variational convolution.
A.Notations
B.Overview
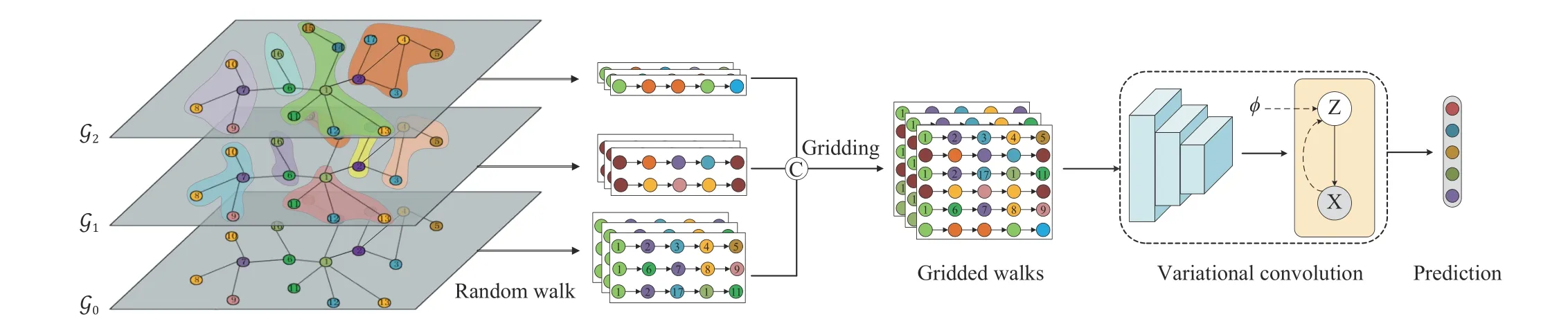
Fig.1.The framework of our proposed VG-GCN.The description can be found in Section III-B.Specifically,G0 denotes the origin graph,and G1,G2 are the coarsened graphs with different coarsening ratios.

Fig.2.Graph coarsening with the coarsen ratio of 0.3.
The overall network framework is shown in Fig.1,where the input is the graph-structured data.To illustrate the convolution process,we take the corresponding local subgraph (i.e.,local receptive field) around one node as an example.In order to aggregate topological information of different levels of nodes,we execute graph coarsening on the input graph according to different coarsen ratios,and then random walk on these hierarchical graphs to capture the local structures;see Section III-C.Through random walk based on hierarchically coarsening,the hcr-walk could effectively mitigate the problem of exponentially-explosive increases of sampled walks incurred in the original random walk as sufficient sampling could well guarantee to cover graph structures.Next,the sampled walks are adaptively gridded into an ordered space through the computation of correlation to the first principal component of random-walks;see Section III-D.The gridding walks are spanned to a 2-D plane ofT×L,which thus favors the conventional convolution.If stacking multi-dimensional signals,the gridded representation of local subgraph is a 3-D tensor ofd×T×L.Thus,the high-efficient and powerful CNNs run on images can be extended for this case to encode the correlation of within-walk adjacencies and cross adjacent walks.To describe the variations of latent feature representation,we introduce variational inference into the 2-D convolution process,referred to as the variation convolution block,to encode the distribution of random-walks therein.Finally,the output features of variation convolution are passed through a fully connected layer and a softmax function for node classification.
C.Hierarchically-Coarsened Random Walk
The random sampling strategy is introduced to characterize the topology structure of local receptive fields.There are two critical questions which need to be solved:i) random sampling should well preserve topology property of original graph,and ii) sampling times should be as few as possible for highefficient computation as well as low-memory requirement.The first condition dedicates to the accuracy of representation,while the second one focuses on the efficiency of learning.Random walk can satisfy the first condition well under the sufficient samplings,but the sampling complexity heavily depends on node degrees during traversals on graph.Given the average node degreemand walk lengtht,the combinatorial number of walks ismt,which has the exponentially-explosive quantity whenmis a bit large(especially density graph) even for a small walk step.For example,supposem=10 andt=8,the combinatorial walks can reach the number of 1 0 000 000 for each staring node.In order to guarantee the accuracy in the first condition,the practical sampling times might be huge even if a small sampling ratio is taken.It will cause high-computation burdens and require high storage space.
To address this problem,we extend the random walk to hierarchically-coarsened random walk by leveraging the powerful topology preservation ability of random walk and the high efficiency of random aggregation.The schematic diagram of graph coarsening is shown in Fig.2.If we useto denote the original graph before coarsening andp1to denote the coarsen ration,the coarsening graph for G1can be represented aswhererepresent the numbers of nodes in G1and G2.Specifically,s atisfymeans round up to an integer.We randomly seeded G1with|V2|c luster seeds based on the coarsen ratiop1,and the nodes in G1converge to each cluster seed according to the adjacency relationship in E1.The connection relation of coarsening graph G2is defined by the connection and the number of connections among the clusters.For example,denote nodeiand nodejin G2,they are composed ofm1andm2nodes in G1
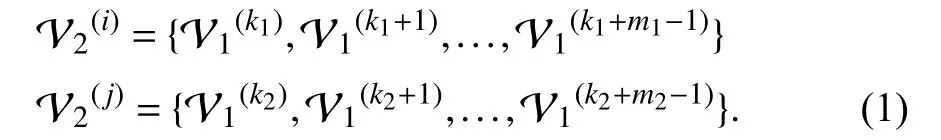
Considering that the number of connections between cluster nodes is not consistent,we processed the coarsening graph into a weighted graph (For consistency,the original unweighted graph can convert to the weighted graph according to the node’s degree).The weightbetweenandcan be computed as
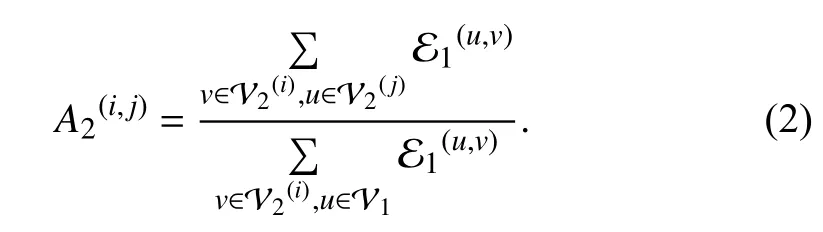
The feature of the node in coarsening graph is related to the nodes belonging to the cluster.In graph learning task,the larger the degree of the node,the more important the node (for example,in social networks,large degree nodes represent popular users and play a more important role in pattern mining).Therefore,the degree of nodes in the cluster can be used as the weight of their feature synthesis

whereDvdenotes the degree of nodev.We construct the hierarchical coarsening graphs by coarsening the input original graph according to different coarsen ratios,and then execute random walk on the original graph and hierarchical graphs.We employ the alias sampling method [56] to sample truncated random walks from the discrete probability distribution in Aifor hierarchical graph Gi,and concatenate the paths which belong to the same start node.The walks on different hierarchical graphs can aggregate the graph topologies with few sampling times,high-efficient computation,and low-memory requirement.
D.Gridding
One problem of the classic random walk is the irregularity along different paths caused by random sampling,which makes it rather challenging to exploit the underlying local correlation across adjacent walks.To solve this problem,we perform gridding on the output features of random-walks to project them into an ordered space.Based on this operation,the gridding paths are spanned to a 2-D plane based on two axes,i.e.,TandL,representing the time of sampling and the number of walk step,respectively.The operation of gridding brings one notable benefit that the high-efficient and powerful CNNs run on images can be extended for the paths to jointly encode the correlation of within-walk adjacencies and cross adjacent walks.For multi-dimensional signals,the gridded representation of local subgraph may be a 3-D tensor ofd×T×L,which is also suitable for the application of CNN.
To adaptively capture the correlation among random paths,we conduct gridding from the perspective of distribution and consider each sampled path based on its correlation to the first principal component of hcr-walk.For the hcr-walk on one node with the representation denoted aswe first split it into a set of path samples denoted as {d1,...,dT} along the sampling time axisT,whereis the vectorized representation of thei-th path sample.For gridding,the clustering center of path samples is first calculated as

Then,the correlation between thei-th path sample and the cluster center is defined as follows:
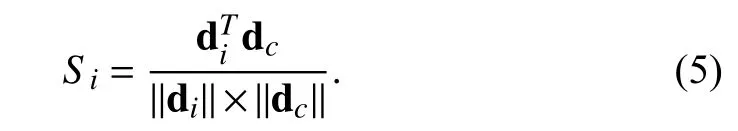
Then,the path of each node is gridded based on its corresponding value correlation related to the cluster center.
E.Variational Convolution
Variational convolution is used to characterize the uncertainty of latent feature representation,which is inspired by the variational inference.We stack multiple 2-D convolutional layers on the ordered grid-like feature mapis the output of gridding operation,andf(·) denotes the convolutional layers.We view the path numberTand the walk lengthLas the height and width in one image,and use the feature dimensiondto represent the in-channel of convolutional layers.Because of the dimensions ofTandLcontain the practical structure significance of the graph,instead of the standard convolution kernel (k×k),we employ an irregular convolution kernel(k1×k2) to better aggregate the neighborhood structure information sampled by the hcr-walk and the node information in different size of receptive field.For one start node,the irregular kernel collects the depth information from theLdimension and the breadth information from theTdimension,which performs as the local aggregation process with an increasing receptive field.Ideally,ifL=2 and the central node’s first neighbor number isT,our convolutional layer is equal to one layer of GCN.
For each start nodevi,we get the feature representationHifrom stacked convolutional layers.Then,we adopt VCB to describe the probability distribution of node’s aggregated feature representation Hi.The structure of VCB is shown in Fig.3.According to the theory of variational inference,the marginal likelihood of Hican be written as
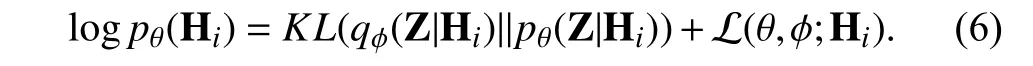

Fig.3.Variational convolution block (VCB).
The first term denotes the KL divergence of the approximate from the true posterior,and the second term L(θ,φ;Hi)is called the variational lower bound.According to the conditional probability formula

and the definition of KL divergence

We can use Monte Carlo sampling [57] to approximate the expectation of the second logarithmic likelihood term in (9),and adopt reparameterization trick (Z=g(H,ϵ),ϵ~N(0,1))to make the process of calculating parameter gradient be differentiable.Let the prior of Z denote the standard normal distribution: Z~N(0,1),the resulting estimator for this model and datapoint Hiis
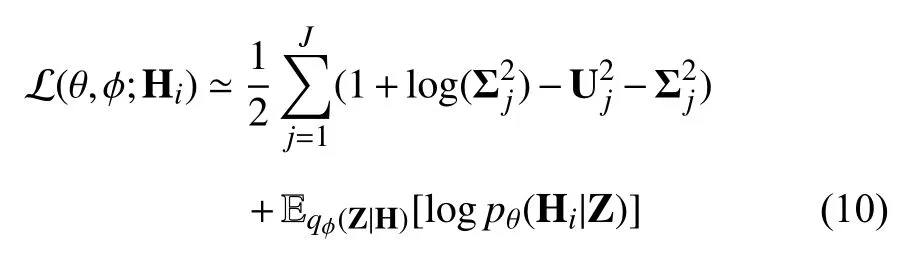

wherejdenotes thej-th feature map,(x,y) denotes the local position of(T,L),k1andk2are the height and width of the kernel,andis the value at the position(p,q) of the kernel connect to thej-th feature map.
IV.ALGORITHM AND ANALYSIS
Our VG-GCN algorithm flow is shown in Algorithm 1.VGGCN is an end-to-end online learning model.The inputs are the adjacency matrices A and feature matrices X of the starting nodes,and the outputs are the corresponding predicted labelsThe loss function L of the model consists of two parts:cross-entropy loss L1and variational lower bound L2in(10).

where α is a hyper parameter.


For each starting node,we sampleTpaths with lengthLin hcr-walks,so as to ensure that the neighborhood nodes could be covered as much as possible.The complexity of VG-GCN iswherenis the number of nodes to be processed (i.e.,training set and testing set),kis thek-th layer,dkis the output dimension of thek-th layer,andk1andk2denote the height and width of convolution kernels,respectively.The complexity of GCN isandN≫nin commons (i.e.,in Pubmed dataset,n=1060 andN=19 717),indicates the speed of our proposed VG-GCN.
V.ExPERIMENTS
In this section,we comprehensively evaluate the effectiveness of our method on five widely used public datasets:Cora,Citeseer,Pubmed [58],AMZ PHOTOS [59],and NELL [60].We first briefly introduce these datasets,then report our experimental results on them and compare the performance with other state-of-the-art methods.Finally,we conduct an ablation study to dissect the proposed model.
A.Datasets
Five public graph-structured datasets are employed to evaluate our proposed method,including three citation network datasets (i.e.,Cora,Citeseer,Pubmed),a co-purchase dataset (i.e.,AMZ PHOTOS),and a knowledge graph dataset(i.e.,NELL).For fair compassion,the dataset split protocols of these citation networks strictly follow the widely used ones in [60].The overall information about these five datasets is listed in Table I.
1) Cora:Cora is a citation network about machine learning papers categorized into seven classes:case-based,genetic algorithm,neural network,probabilistic method,reinforcement learning,principle learning,and theoretical.In total,Cora contains 2708 nodes and 5429 edges,where each node can be described by a 1433 dimensional vector consisting of0/1-valued elements.The average degree of nodes in Cora is about four.For the protocol on this dataset,there are 5.2% of nodes labeled for training (20 nodes in each class,140 nodes in total),500 nodes for validating,and 1000 nodes for testing.

TABLEI GRAPH DATASETS INFORMATION
2) Citeseer:Citeseer depicts a citation network of 3327 nodes and 4732 links,where the nodes are divided into six classes.Each node can be described by a 3703 dimensional 0/1-valued vector.For evaluation,3.6% nodes are labeled for training (20 nodes in each class,120 nodes in total),and the numbers of nodes in the validation and test sets are 500 and 1000,respectively,which are as same as those in Cora.Each node in Citeseer is connected by three nodes in average.
3) AMZ PHOTOS:AMZ PHOTOS is a Co-purchase dataset.It contains 7487 nodes of 8 classes with 119 043 edges.Each node is described by a 745 dimensions vector,and the average degree of nodes is 32.This dataset is split by 200/4800/2487 for train/val/test.
4) Pubmed:Pubmed contains 19 717 nodes of three classes with 44 338 edges.Each node is described by a term frequency-inverse document frequency (TF-IDF) vector drawn from a dictionary with 500 terms.For the widely accepted protocol on this dataset,there are only 0.3% of nodes for training (20 nodes in each class,60 nodes in total),500 nodes for validating,and 1000 nodes for testing.The average degree of each node is about five.
5) NELL:NELL dataset is extracted from the never ending language learning (NELL) knowledge graph [61].Each relation in NELL links the selected entities (9897 in total)with text descriptions in ClueWeb09 [62],and can be described with a triplet (eh,r,et) whereehandetare the head and tail entity vector,andrdenotes the relation between them.By splitting every triplet (eh,r,et) into two edges (eh,r1) and(et,r2),a graph of 65 755 nodes (including relations and entities) and 266 144 edges can be obtained,where each node can be described by a 61 278 dimensional vector and approximately connected by four nodes.
B.Baseline Methods
To verify the superiority of our proposed VG-GCN model,various state-of-the-art methods are used for performance comparison.Basically,the results of these baseline methods are obtained either according to their reported performance in previously literatures,or through conducting the experiments based on their released public codes.For the baseline methods of our implementation,sophisticated hyper-parameter finegrained tuning is performed to report their performances.
DeepWalk [48] is a generative model for graph embedding,which samples multiple walk paths from a graph by the truncated random walk,and learns the representation by regarding the paths as sentences,and path nodes as tokens in natural language processing (NLP).The source code for DeepWalk is publicly available1https://github.com/phanein/deepwalk.Planetoid [60] is inspired by the Skipgram [53] model from NLP,and it embeds a graph through both positive and negative samplings while considering the node information and graph structure.The source code of Planetoid is available2https://github.com/kimiyoung/planetoid.Chebyshev [16] designs a fast localized graph convolution by employing localized filters with polynomial parametrization,and adopts graph coarsening procedure to group together similar vertices.Graph convolutional networks (GCN) [17] updates the feature expression of the central node by synthesizing the information of the gradually expanding sensing nodes in the field.GCN’s source code is publicly available3https://github.com/tkipf/gcn.Graph attention networks(GAT) [31] applies the attention mechanism to graph convolution.It calculates the attention coefficient between central node and its neighborhood nodes to express the different contribution of neighbor connections.Moreover,GAT has an additional sparse version which is also involved as the baseline.For these two versions of GAT,the performance is reported in Table II.GAT’s source code is publicly available4https://github.com/PetarV-/GAT.Dual graph convolutional networks(DGCN) [63] executes dual graph convolution based on the adjacency matrix and positive pointwise mutual information(PPMI) matrix,respectively,and combines the output of different convolved data transformations.The source code of DGCN is publicly available5https://github.com/ZhuangCY/DGCN.Graph learning-convolutional networks (GLCN) [64] learns a discriminativeSto replace the adjacency matrixAfor graph convolution based on the topological between nodes and on high-dimensional manifold.gLGCN [65] adds the local invariance constraint to the loss function that the same label samples should have the same data distribution.Hypergraph neural networks (HGNN) [66]designs a hypergraph structure,where one edge can connect multiple nodes.Then,robust node representation can be learned by aggregating the node information to the hyper-edge and then returning the integrated information to each node.
C.Experiment Setting
The parameters of our VG-GCN model are traversed in certain ranges and finally set when the best performance on the validation set is obtained.For the basic architecture of the VG-GCN model,there are two convolutional layers in VCB.The coarse layers number is 2 and the coarse ratios are 0.8 and 0.4,respectively.In the hcr-walk process,the number of walks,denoted asT,is set to 15,and the hcr-walk lengthLis5.For the convolutional layers,the sizes of convolution kernels are set to 5×3,while in the VCB the convolution kernel sizes are both set to 1×1 to produce the mean and covariance matrices,respectively.During the training process,we run the model for 500 epochs with the learning rate of 0.01 and dropout rate of 0.5 for tuning the network parameters.

TABLEII PERFORMANCE OF GRAPH NODE CLASSIFICATION, COMPARED WITH DEEPWALk, PLANETOID, CHEBYSHEV, GCN, GAT,DGCN, GLCN, GLGCN, AND HGNN METHODS
D.Experiment Results
The experimental results of our proposed VG-GCN on the three citation datasets (Cora,Citeseer,and Pubmed),one copurchase dataset (AMZ PHOTOS),and large-scale dataset of knowledge graph (NELL) are reported in Table II.These performances are also compared with various state-of-the-art methods,where the metric of accuracy is employed for quantitative evaluation of the semi-supervised node classification.Our VG-GCN obtains the best results on AMZ PHOTOS,Pubmed,and NELL datasets (there are 0.05%performance gain on AMZ PHOTOS,1.2% on Pubmed,and 4.2% on NELL),and achieves the competitive performances on the Cora and Citerseer datasets.
We calculated the average and variance of node degree of five datasets.We found that the degree variances of two small datasets (Cora and Citeseer) are small (27.3 and 11.4,respectively),while the other three large scale datasets (AMZ PHOTOS,Pubmed,and NELL) have the larger degree variances (55.2,1852.3,and 2262.6,respectively).Therefore,we speculate that the reason our VG-GCN does not achieve the best performance on the two small datasets may be that the two dataset have fewer random walk patterns and are more likely to fall into over-smoothing during the training process.This also shows that our hierarchical coarsening and random walk can model complex data patterns.
Besides the competitive performance,it should be especially noticed that our model is more advantageous in computation efficiency compared with all other baseline methods.We present the time costs of our VG-GCN for running one epoch on Cora and Pubmed datasets in Table III,and compare them with GAT,DGCN,and GCN.For Cora,the smallest dataset,GAT takes about 7 s per epoch while its sparse version takes 1 s,and DGCN takes about 0.5 s per epoch.The time consumed by our VG-GCN is 0.05 s,which is much less than those of GAT and DGCN,while almost the same as GCN.However,on the large graph Pubmed (19 717 nodes),our VG-GCN takes about 0.04 s per epoch,and is the fastest compared with the sparse GAT of 2.5 s per epoch,DGCN of 3.2 s,and GCN of 0.6 s.

TABLEIII EACH EPOCH TIME COST ON CORA AND PUBMED, COMPARED WITH GAT, DGCN, AND GCN
The convergence of our VG-GCN on the Nell datasets is shown in Fig.4,and is compared with that of DGCN which also achieves a considerable performance.Both VG-GCN and DGCN are trained 1000 epochs on NELL dataset.According to Fig.4,our VG-GCN can converge faster and obtains better performances.In terms of running time and accuracy comparisons,our VG-GCN takes about 6 minutes with the accuracy of 79.1%.In contrast,DGCN takes about 2.8 hours,which is 29.2 times that of VG-GCN,while obtaining an accuracy of 74.9%,which is 4.2% lower.

Fig.4.The convergence on NELL datasets,compared with DGCN.
E.Ablation Study and Parameter Sensitivity
As the proposed VG-GCN achieves promising performance with high computational efficiency,it is interesting for us to dissect the model to evaluate the contribution of each part.Moreover,it is also meaningful to evaluate the sensitivity of those critical parameters in the VG-GCN model to make clear how their variation influences the performance.Therefore,we conduct several additional experiments:
1) Comparison between the hcr-walk and random walk.To verify the superiority of the proposed hcr-walk over random walk,we simply replace the hcr-walk unit with random-walk on original graph,and test the performance on the four public datasets.The results are shown in Table IV.

TABLEIV COMPARISON BETWEEN HCR-WALk AND RANDOM-WALk
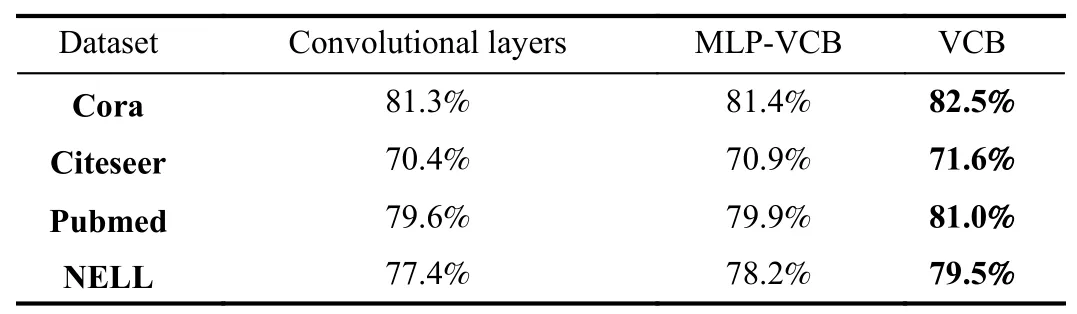
2) Evaluation of VCB.To evaluate the effectiveness of the proposed VCB,we compare its performance with the classic convolutional layer and MLP-VCB on the four datasets,and the results are shown in Table V.Specifically,MLP-VCB means that the calculation of mean and covariance matrices in VCB are revised to be obtained through multilayer perception instead of convolutional layers.
TABLEV COMPARISON OF CONVOLUTIONAL LAYERS, MLP-VCB, AND VCB
Based on the results of the multiple experiments above,we can get the following observations:
1) Hcr-walk outperforms classic random walk and promotes the node classification performance.On all the four evaluated datasets,the classification accuracies of our hcr-walk are higher than those of random walk.The performance gain verifies the effectiveness of our hcr-walk,which constructs coarsening graphs,while avoiding an explosive growth of walk paths with increasing walk steps.
2) VCB is effective to promote the node classification task.Comparing with both convolutional layers and MLP-VCB,VCB obtains better node classification performances with an average performance gain of about 1% on the four public datasets.The performance improvement verifies the superiority of VCB,which encodes the comprehensive correlation of within-walk adjacencies and cross adjacent walks.
Kernel sizek1,k2,hcr-walk numbersTand lengthL,and coarsening ratiopare hyper parameters in VG-GCN.To analyze the sensitivity and value selection of each hyper parameter,we designed the following comparative experiments.
1) Kernel Size:The non-square 2D convolution kernel is employed in hcr-walk convolution.The different classification performance with different kernel sizes on three citation datasets is plotted in Fig.5.From the experimental results of Fig.5,the irregular convolution kernel with size (5,3) has better performance on three datasets.Specifically,(5,3)means the cross-path filtering height is 5 and within-path filtering width is 3.

Fig.5.Classification performance with different kernel sizes on three citation datasets.
2) Hcr-Walk Numbers and Length:The parameter sensitivity experiments with the hcr-walk numbersTand hcrwalk lengthLbelonging to one start node are shown in Figs.6 and 7.For Cora dataset,15 hcr-walks are sampled for each node,and the length of 5 is the most appropriate.(T=20,L=5) and (T=12,L=6) are the best combinations of parameters for Citeseer and Pubmed datasets,respectively.
3) Coarsening Ratio:The hierarchically-coarsened random walk is employed to leverage the powerful topology preservation ability of random walk and the high efficiency of random aggregation.We experimentally compare the effects of one coarsening layer,two coarsening layers and different coarsening ratiospon the classification accuracy of Cora dataset in Table VI.For the two coarsening layers,the coarsening ratio of the second layer is half of the first.Two coarsening layers with ratios of (0.8,0.4) achieve the best performance.

TABLEVI SENSITIVITY OF COARSEN LAYER NUMBER AND COARSE RATIO ON MODEL PERFORMANCE ON CORA DATASET.FOR TWO COARSEN LAYERS, WE SET THE COARSEN RATIO OF SECOND LAYER IS HALF OF FIRST LAYER

Fig.6.The results of VG-GCN model with different hcr-walk numbers on Cora,Citeseer,and Pubmed datasets.

Fig.7.The results of VG-GCN model with different hcr-walk lengths on Cora,Citeseer,and Pubmed datasets.
4) Convolution Layers:The number of variational convolution layer is traversed in [2,8] on Cora dataset,and the experiments results are listed in Fig.8.The experimental results show that the too deep network can not surely achieve higher classification accuracy,and may cause performance degradation which may be due to the over-smoothing.

Fig.8.The results of different variational convolution layers on Cora dataset.
In order to show that our VG-GCN can better capture the graph local invariance than other methods (GCN),we perform a standard set of“evolving”t-SNE [67] plots of the test set embeddings on Cora dataset,given in Fig.9.The raw features come from the node original feature matrix,and the GCN and our VG-GCN embeddings come from the output of the last layer respectively.Intuitively,our VG-GCN is best placed to clearly separate different categories of nodes.And from the perspective of quantitative analysis,the Silhouette score [68]of our VG-GCN is the largest (The larger the Silhouette score,the better the clustering effect).
VI.CONCLUSION
In this paper,we proposed a VG-GCN framework for node classification.We developed the random walk and proposed the hcr-walk to effectively avoid possible exponential explosion of walk paths as the path length increases,and cover the whole neighborhood by coarsening graphs.In order to maintain the permutation invariance of the generated paths belonging to the same node of each epoch,we sorted them after projection and constructed a grid-like feature map for 2-D convolution.Moreover,we designed a 2-D convolution variational inference block to learn the probability distribution characteristics of latent variables in two-dimensional space.As a result,VG-GCN learns the aggregation pattern of node topological neighborhood in an inductive way,which can be easily extended to the inference problem of unknown nodes.Meanwhile,VG-GCN can process large scale graphs quickly with the tensor graph structure and consumes less memory.Experiments on a variety of public datasets verified the effectiveness of our method for solving the node classification problem.

Fig.9.t-SNE embeddings of the nodes in the test set of Cora citation network from the raw features (left),GCN model (middle),and our VG-GCN model(right).Our VG-GCN performs the best clustering effect of embedding among the three plot,and the Silhouette scores support evidence.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Limited-Budget Consensus Design and Analysis for Multiagent Systems With Switching Topologies and Intermittent Communications
- Reduced-Order Observer-Based Leader-Following Formation Control for Discrete-Time Linear Multi-Agent Systems
- Distributed Order-Up-To Inventory Control in Networked Supply Systems With Delay
- Hierarchical Reinforcement Learning With Automatic Sub-Goal Identification
- Theory and Experiments on Enclosing Control of Multi-Agent Systems
- Command Filtered Finite/Fixed-time Heading Tracking Control of Surface Vehicles
