漂浮式海上风电塔新型基础设计

2021-10-25宋波周恒王道永

船海工程 2021年5期

宋波，周恒，王道永

(北京科技大学 a.土木与资源工程学院;b.强震区轨道交通工程抗震研究北京市国际科技合作基地,北京 100083)

近年来，漂浮式海上风电塔因其适用水深范围广、安装运输方便而备受关注[1]。漂浮式基础是海上风电塔结构的重要组成部分。目前广泛使用的漂浮式海上风电塔基础结构形式[2]，图1。

图1 漂浮式风电塔基础结构示意

图1a)所示的单立柱基础结构优点是结构形式简单，缺点是具有较高的自由度和不稳定性。图1b)所示的张力腿基础结构优点是稳定性好，缺点是张力腿一直处于绷紧状态，基础设计较复杂。图1c)所示的三浮体基础结构优点是结构简单，缺点是基础整体尺寸太大，锚泊系统过于复杂。海上风电场运行环境复杂，慎重选择海上风电塔基础的结构形式，并进行合理设计，是海上风电场建设的关键[3]。针对漂浮式海上风电塔，借鉴力学原理，提出一种新型的半球壳基础结构形式。利用ABAQUS有限元分析软件建立风电塔结构与基础模型，探究使用该种新形式基础的漂浮式海上风电塔的稳定性能，以验证半球壳结构形式的漂浮式基础的可行性。

1 工程概况

以江苏环港某海上风电场为背景，该区域离岸距离约10 km，水深约58 m，抗震设防烈度为7度，场地类别为Ⅱ类，设计地震分组为第Ⅲ组，设计基本地震加速度值为0.1g。塔身为变截面、变壁厚筒状结构，材料为Q345C钢，塔筒底部最大厚度为50 mm、顶部最小厚度为20 mm。风电塔结构基本计算数据如下。

轮毂高度56.6 m；风轮直径72.3 m；

上部结构质量129.8 t;塔筒质量156.1 t；

塔顶直径3.1 m；塔底直径4.5 m。

2 风电塔基础结构形式设计

2.1 不倒翁结构及其原理

不倒翁是一种上半身为半球壳，下半身为实心球体的物体，底部为圆形，其结构上轻下重，重心位于半球体内。不倒翁在受到外力作用发生倾斜时，其重心不断升高，并受到2个力矩的作用，如图2所示。由外力产生的力矩为干扰力矩，另一个为抵抗力矩(也称扶正力矩)，是由其自身重力产生。随着不倒翁倾斜的角度不断增大，重力作用线的偏移量随之增大，抵抗力矩也随之增大，最终和干扰力矩相互平衡。此外，不倒翁底部为圆形，摩擦力小，利于不倒翁回到原来的位置。

图2 不倒翁原理示意

2.2 基础尺寸的拟定

风电塔塔筒底部与基础顶部通过高强螺栓锚固连接，在基础中间部位设置一圆形支撑，以降低基础的重心并提高其稳定性。基础通过锚链与海床相连，以增加海上风电塔结构的整体抗倾覆能力。结构整体示意于图3。

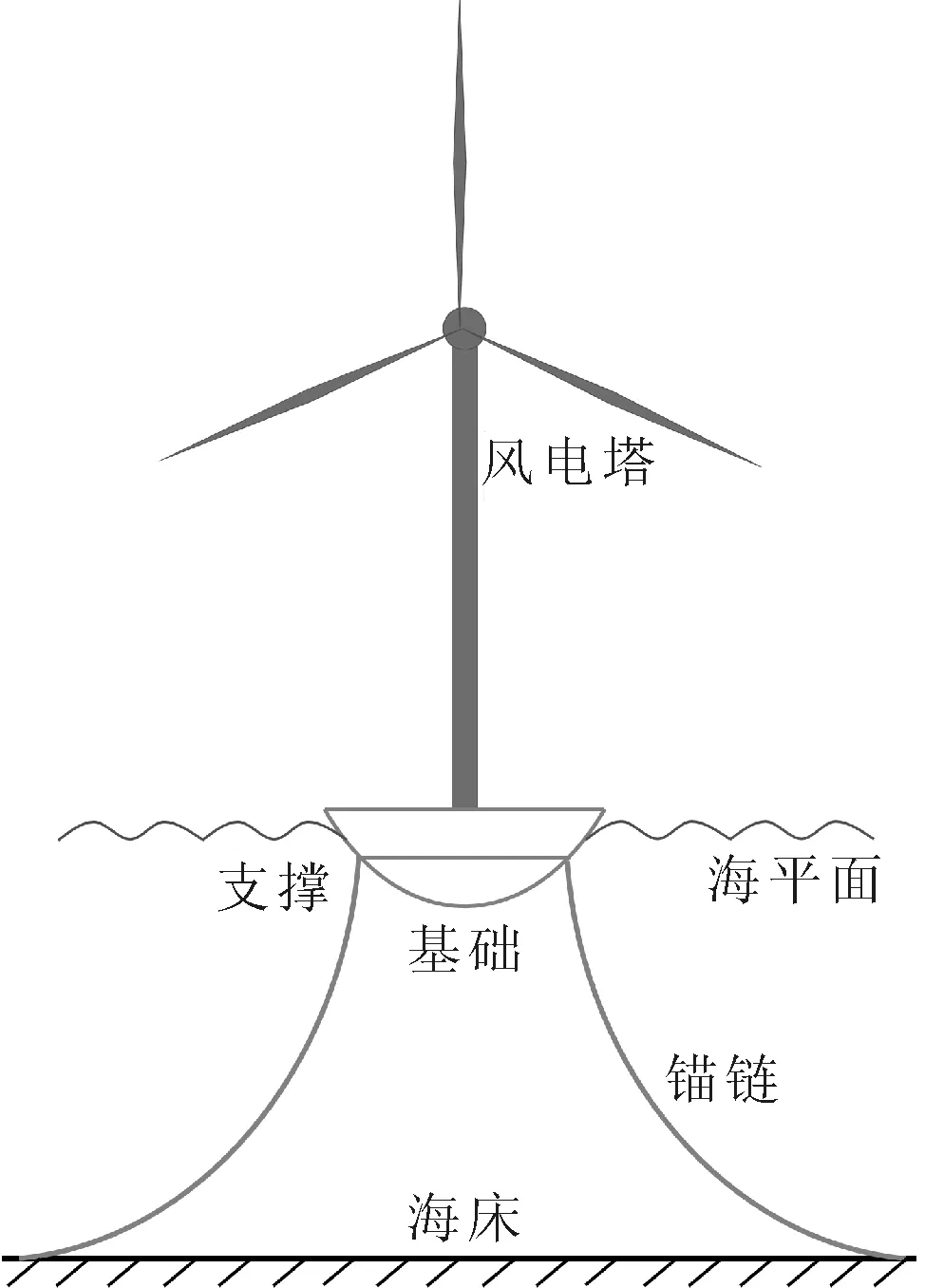
图3 海上风电塔和基础结构示意

该基础结构形式为半球壳，基础外轮廓为一半球形。假定漂浮式基础采用DH32钢材，厚度为10～30 mm，基础半径为15 m，中间圆形支撑厚度为10 mm，计算得基础总质量为225.3 t。漂浮式风电塔结构整体质量为511.2 t。

对所选基础尺寸进行验证。为保持平衡，风电塔结构所受浮力需与重力相等，即所受浮力为5 004.8 kN。根据阿基米德定律计算可得风电塔基础排水体积为511.2 m3。

3 动力响应分析

3.1 漂浮式海上风电塔结构模型建立

利用ABAQUS有限元软件对风电塔结构进行建模。基础采用S4R壳单元划分网格；塔筒、机舱与叶片采用C3D8R实体单元划分网格；轮毂采用C3D10实体单元划分网格；各个部件之间均采用绑定约束。对于海洋采用欧拉体进行模拟，模型尺寸足够大，忽略边界条件的影响，单元类型为EC3D8R[4]；锚链采用T3D2桁架单元划分网格。结构的整体有限元计算模型见图4。

图4 结构整体有限元模型

3.2 波浪载荷的选取

波浪是影响漂浮式海上风电塔稳定性的重要因素。采用线性波理论计算方法[5]。简化的线性波波面见图5。

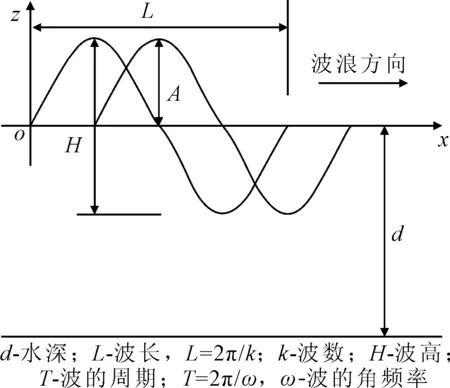
图5 线性波波面示意

线性波用余弦公式表示为

η=Acos(kx-ωt)

(1)

式中：A为幅值；t为时间。

根据线性波理论，水质点运动时，x方向速度为

(2)

式中：γ为波浪的传播方向与x轴的夹角；

水质点运动时，x方向加速度用为[6]

(3)

根据线性波理论在结构整体模型中输入波浪载荷，进行漂浮式风电塔结构的动力响应分析。

3.3 风电塔结构模态

将锚链-基础-塔筒-机舱-风轮作为整体，对结其进行模态分析，得到结构前6阶频率f与周期T，见表1。

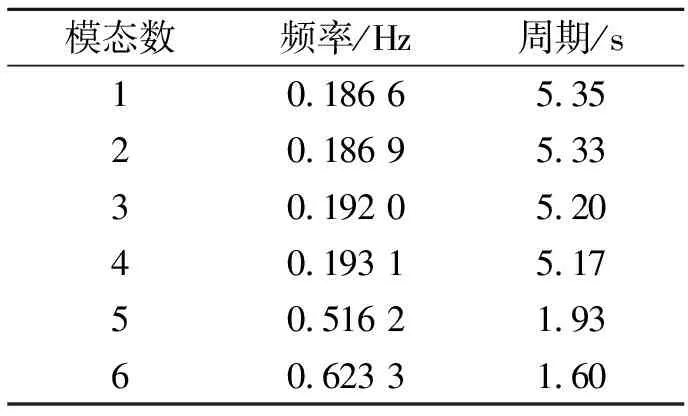
表1 风电塔结构前6阶模态

风电结构的1阶振动模态反映了漂浮式风电塔上部结构的弯曲变形，结构第2阶至第4阶自振频率与第1阶自振频率相差不大，其振型仍为上部结构的弯曲变形振动；从第5阶模态开始，结构的振型频率明显增大，结构开始出现上部结构的二次弯曲与下部基础和锚链的组合变形。

3.4 考虑不同波浪载荷的作用

在有限元模型中输入波浪载荷，载荷作用于欧拉体上，载荷作用方向与结构风轮面垂直。选取波浪等级为微浪、轻浪、中浪和巨浪，浪高分别为0.1，0.5，1.25，4 m[7]。根据风电塔结构的基本周期，选定波浪载荷作用时间为12 s。目前只考虑几何非线性进行结构的稳定性分析。

风电塔结构在微浪荷载作用下位移时程见图6。

图6 微浪载荷下风电塔结构位移时程

目前关于漂浮式风电塔的安全评价标准尚未成熟，一般规范中并没有对漂浮式风电塔的倾角限值做出规定，但为了保证风电塔关键设备的正常运行，有必要设置风电塔倾角最大限值。借鉴传统海工平台规范，参考DNVGL发布的漂浮式风机设计标准[8]，这里采用漂浮式风电塔正常工作时倾角限值5°。

由图6计算得到微浪作用12 s内，风电塔结构底部与顶部最大位移差值为0.21 m，最大倾斜角为0.22°。

风电塔结构在轻浪荷载作用下位移时程见图7。

图7 轻浪载荷下风电塔结构位移时程

由图7计算得到轻浪作用12 s内，风电塔结构底部与顶部最大位移差值为0.43 m，最大倾斜角为0.45°。

风电塔结构在中浪作用下风电塔位移时程见图8。

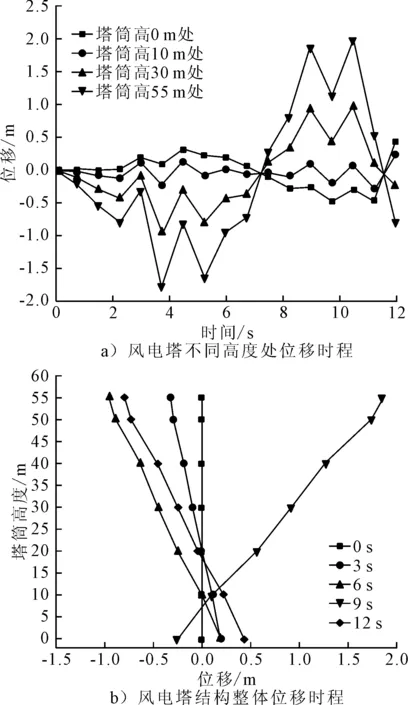
图8 中浪载荷下风电塔结构位移时程

由图8计算得到中荷作用12 s内，风电塔结构底部与顶部最大位移差值为2.42 m，最大倾斜角为2.6°。

风电塔结构在巨浪作用下的位移时程见图9。

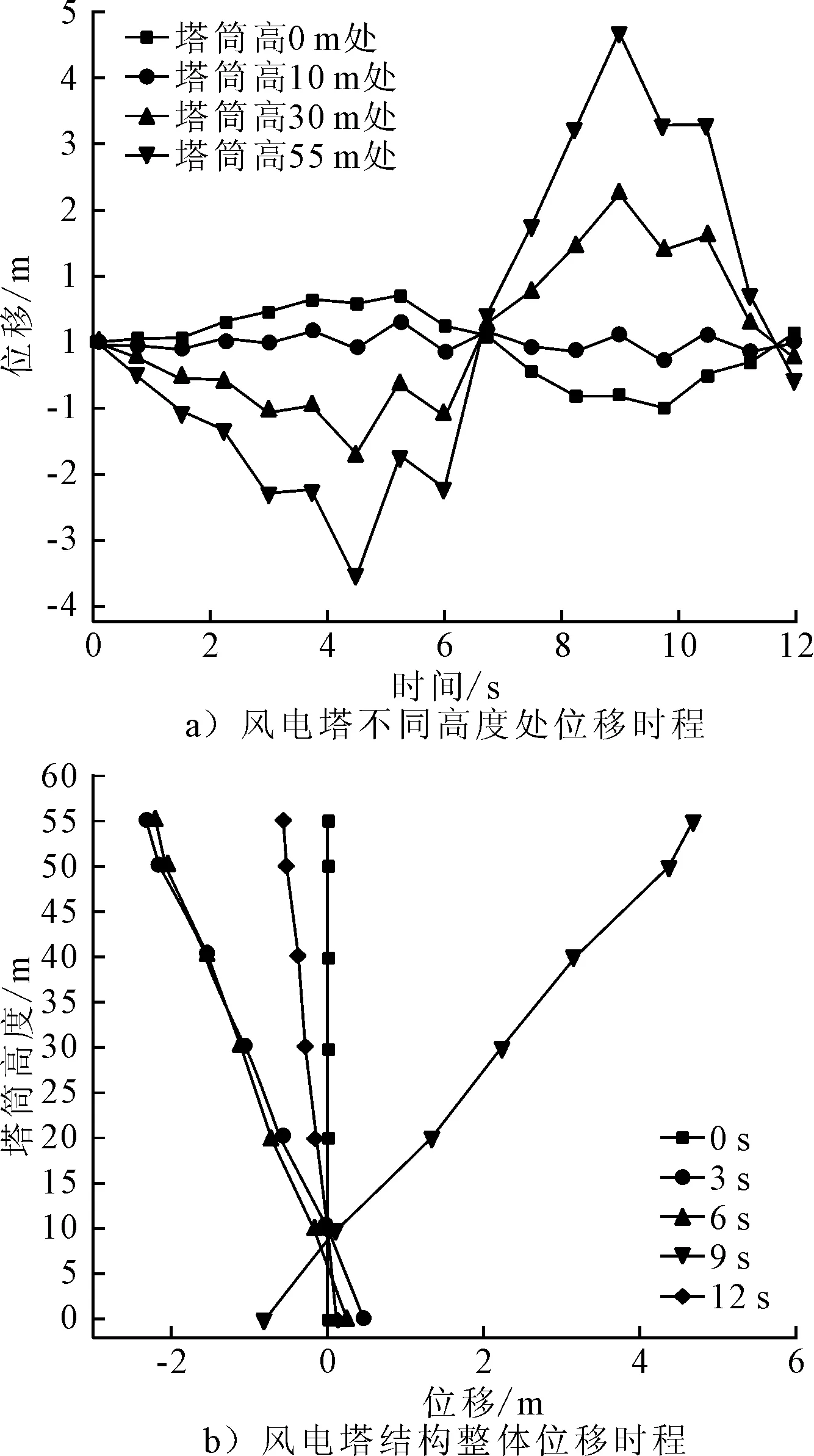
图9 巨浪载荷下风电塔结构位移时程

由图9计算得到巨浪作用12 s内，风电塔结构底部与顶部最大位移差值为4.69 m，最大倾斜角为4.8°。

由图6～9可知：这种新基础形式的海上漂浮风电塔在微浪、轻浪与中浪载荷作用12 s内，最大倾斜角分别0.22°，0.45°，2.6°，均满足漂浮式风电塔倾斜角限值5°的要求，风电塔结构具有良好的稳定性；在巨浪载荷作用12s内，风电塔结构发生大幅度晃动，最大倾斜角为4.8°，虽然接近漂浮式风电塔倾斜角5°的限值，但仍满足漂浮式风电塔设备正常运行的要求，不会出现倾覆或沉没，初步证明这种半球壳形式漂浮基础可行。