基于相关性分析和主成分分析的基因调控网络研究

董 艺，路云龙

(北华大学 数学与统计学院，吉林 吉林 132013)

随着生物芯片技术[1]的发展，基因芯片的信息挖掘成为生物信息学的一个研究热点，人们从研究基因测序[2-3]转而研究基因功能.基因调控网络是一个抽象概念，指细胞内(或特定一个基因组内)两基因之间的相互作用关系所形成的网络，在众多相互作用关系之中，又特指基于基因调控所导致的基因间作用.研究基因调控网络，建立基因调控网络模型，就可以对一个组织或一个生物的全部基因关系进行整体的模拟、分析和探索，进一步在整体基因的框架下研究生命现象和信息流动的规律，所以研究基因调控网络具有重要的现实意义.

目前人们对于基因调控网络的研究处于蓬勃发展的阶段.20世纪中期，Rater首先提出了控制原核生物细胞内基因之间相互影响和相互作用的系统和特征.20世纪60年代，Kauffman构建基因调控网络.许多基因网络模型相继被提出,如布尔网络模型[4]、贝叶斯网络[5]、微分方程网络模型[6]等.这些模型都有各自的优势,然而也存在一些不足.如布尔网络模型使用方便，但容易出现信息缺失问题；贝叶斯网络在寻优的过程中已出现计算成本过大、计算困难的问题；微分方程方法易出现数据噪音不能控制的问题.相关性分析方法也是建立基因调控网络的一个有效工具[7-8]，通过确立基因间是否存在相关性来构建基因调控网络.文章利用主成分分析法确立剪边原则，对相关分析法得到的初始基因网络进行修剪，建立最终的基因调控网络，并对结果进行分析.

1 基因调控模型及方法

1.1 基因网络模型

基因的表达在调节生命活动中充当着重要的角色，在一个生物体中，任何细胞都带有同样的基因，但是，一个基因在不同组织、不同细胞中的表现并不一样，这是由基因调控机制所决定的.基因网络是由大量的基因构成的，这些基因间又存在着复杂的相互作用，这种相互作用是通过他们所产生的蛋白质水平来呈现的，进而构成了基因调控网络.其可以简化成有向图表示,如图1所示,其中节点表示基因,边表示基因间的调控关系.研究基因网络就是为了探索生物或组织中基因间的相互作用关系,以此来认识生命结构,找到生命间的基本规律.

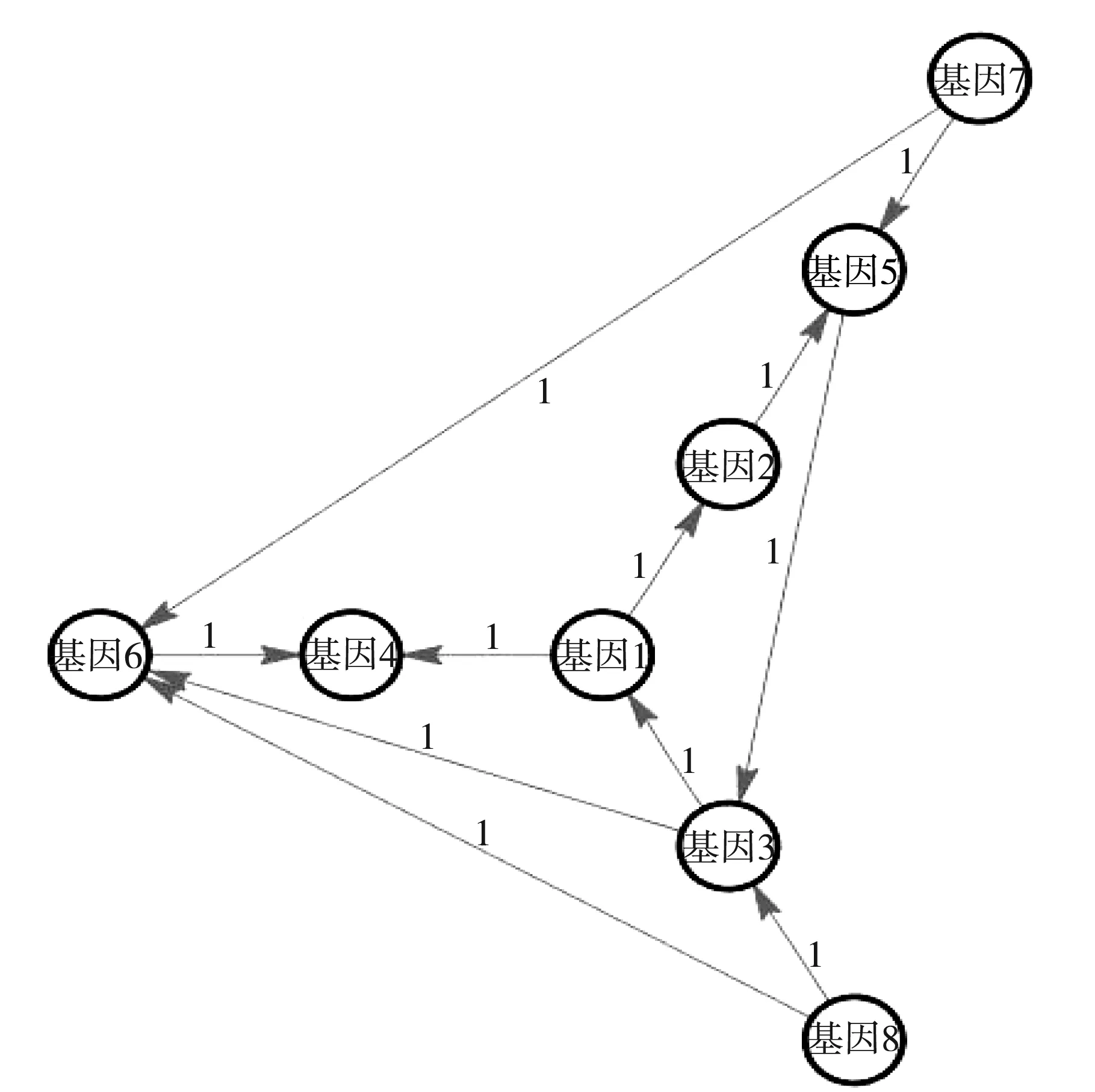
图1 基因调控网络

1.2 双变量相关性分析模型

相关性分析[9]是不考虑变量之间的因果关系，而只研究分析变量之间的相关关系的一种统计分析方法，包括偏相关分析、距离分析等，这里只对于双变量相关分析进行研究并用其解决相关问题.双变量相关分析中主要的相关系数有皮尔逊系数、斯皮尔曼系数以及肯德尔系数.皮尔逊相关系数相比斯皮尔曼系数、欧几里得距离、曼哈顿距离、切比雪夫距离的预测具有较高的准确率[10-11].皮尔逊相关系数主要是衡量两个变量的依赖性的非参数指标，对于样本容量为n的样本，n个原始数据被转换成等级数据，其计算公式为：

(1)

公式(1)主要是用其来判别两基因之间的线性关系.若相关系数ρ=0，则x与y之间无线性关系；相关系数越接近-1或1，相关度越强，相关系数越接近0，相关度越弱.具体标准见表1.

表1 相关系数的判别

1.3 评价标准

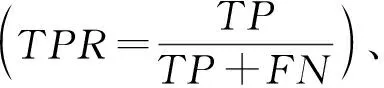
除上述指标外,还有ROC(Receiver Operating Characteristic)曲线和其曲线下的面积AUC(Area Under Curve)来比较不同算法构建基因网络的能力.通过计算上述指标来判定所得到的结果是否成立及其所建立的模型是否合理.

2 基于相关性分析和主成分分析的基因调控网络构建

下面给出主成分相关分析的基因调控网络构建的基本过程.具体步骤如下：

第1步：录入数据；

第2步：验证数据是否服从正态分布；

第3步：对数据进行相关性分析得到相关系数表，利用公式(1)和表2画出初始的基因调控网络；

第4步：对数据进行主成分分析.首先确定“影响小”的结点：在任意一个主成分的评价函数中系数的绝对值小于等于一个正常数时，认为此点对该主成分的影响较小，即为“影响小”的结点；其次，假定影响小的结点引出的不显著相关的边需要进行剪边，即对于与此点相关但相关性不强(表2)对应的边进行剪边，否则不剪边.输出最终剪边后的基因调控网络；

第5步：模型评价.

3 实验结果与分析

3.1 DREAM数据

文章中用到的基因表达数据来源于DREAM项目中的challenge3(https://dreamchallenges.org/dream-3-gene-expression-prediction/),用于推断模拟基因调控网络.利用DREAM3网络中的大肠杆菌(Ecoli1)基因表达数据，包含10个基因，样本数量为10.图2是黄金标准下Ecoli1的基因网络，共11条边.

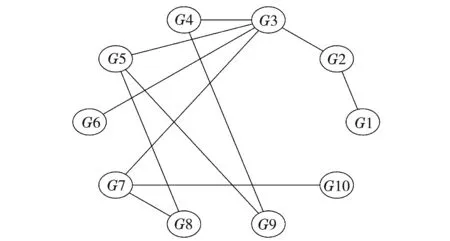
图2 黄金标准下Ecoli1的基因网络

3.2 实验结果与分析

下面利用上述第2节的方法进行测试.

首先验证基因数据是否服从正态分布，结果如图3所示.

图3 数据的柱状图

由图3可以看出数据服从正态分布，接着利用SPSS软件进行相关性分析，得到如下表2所示的相关性矩阵.

表2 相关性矩阵

利用表2的皮尔逊相关系数矩阵和表1的相关系数判别标准得到初始基因调控网络，如图4所示.

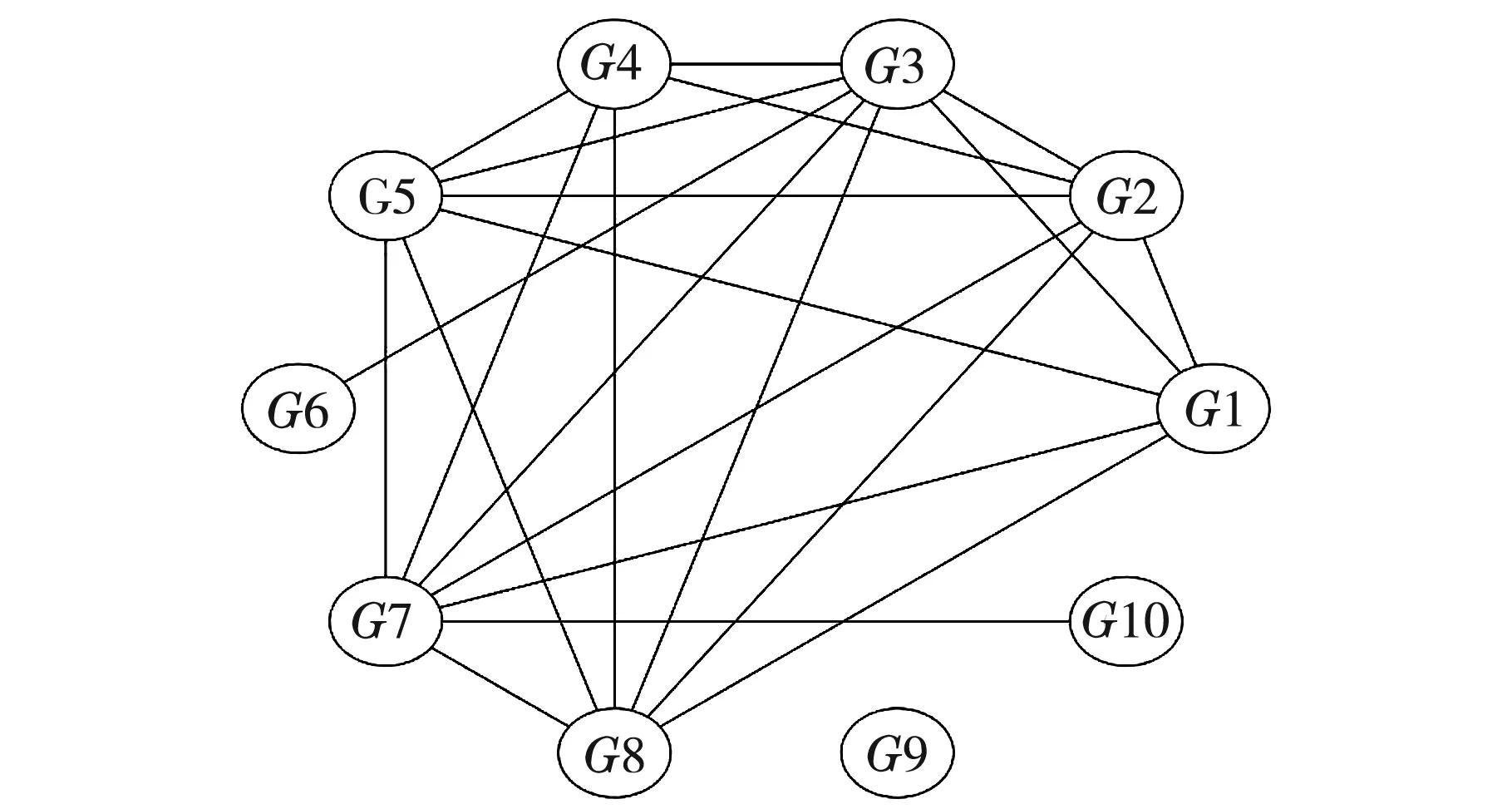
图4 初始基因调控网络

如图4所示,只进行相关性分析后得到的基因网络与黄金标准下的基因调控网络相差较大，有较多多余的边，因此考虑利用SPSS对数据进行主成分分析，得到的总方差解释率如表3所示.

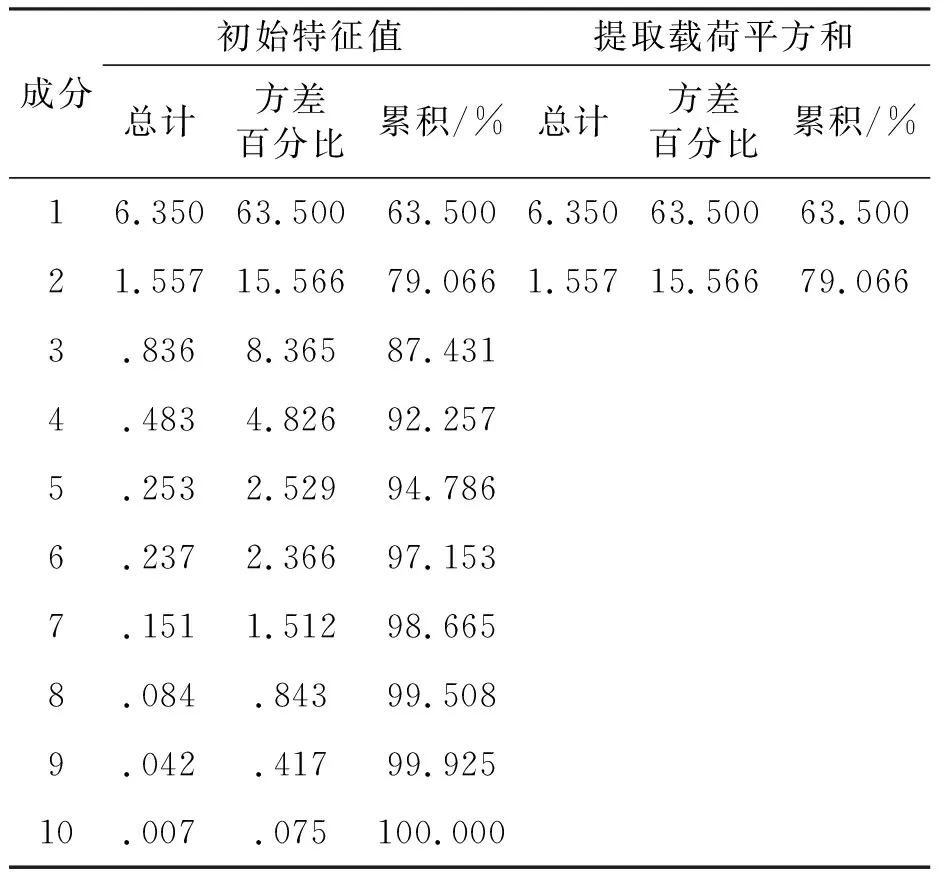
表3 总方差解释

提取方法：主成分分析法.

从表3可以看出前两个主成分的累计方差解释率达到79.066%，因此在1～10基因中得到两个主成分:

Z1=-0.737G1+0.941G2-0.954G3+0.911G4+0.955G5+0.419G6-0.856G7+0.947G8-0.032G9+0.679G10，

Z2=0.501G1-0.045G2+0.119G3+0.038G4-0.204G5+0.737G6-0.188G7-0.103G8-0.690G9+0.426G10.

参考上述主成分函数，根据算法第4步，可知G2、G3、G4、G5、G7、G8、G9前的系数有小于正常数0.25的情形出现，就认为这些结点是“影响小”的结点.结合相关系数表2和图4进行剪边，与“影响小”的结点G2、G3、G4、G5、G7、G8、G9相关但相关系数小于0.8的边G1-G3、G1-G5、G1-G7、G1-G8、G2-G4、G2-G5、G2-G7、G2-G8、G3-G8、G4-G7、G4-G8、G5-G7、G7-G8均需被剪掉，从而得到一个新的基因调控网络，如图5所示.

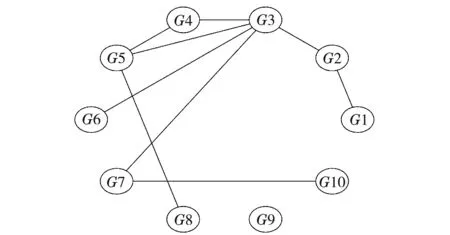
图5 剪边后的网络

根据图5所示结果，经过相关性分析和主成分分析在10个基因中得到9条边，其中有8条边是正确的，G4-G9、G5-G9、G7-G8是缺失的边,G4-G5是多添加的边.相关性分析和主成分分析的实验结果，如表4所示.

表4 实验结果

结合表4可知该方法正确的边较多，准确率较高.因此，相关性分析和主成分分析对于构建小规模基因网络的能力较强、效果较好.

4 结 论

文章首提出相关性分析和主成分分析结合的基因网络调控模型，对DREAM3、data10中Ecoli1的10个基因进行测试，与黄金标准网络相比准确率较高，说明此方法对于少量基因的基因调控网络构建的效果较好.另一方面，相关性分析和主成分分析虽然能够显示变量间是否相关以及相关性强弱的问题，但是相关性分析只能定性而不能定量，从而这种关系是促进还是抑制，存在怎样的表达都无法确定，也不能给出有向的基因调控网络图，这是此方法存在的局限性.另外，在算法中有关阈值的设定还需进一步检验.因此对于基因调控网络的研究，路途遥远，将来还会做进一步的探索.