基于反步法的板球系统自抗扰控制器设计

韩光信，孟圣钧，万云波

(1.吉林化工学院 信息与控制工程学院，吉林 吉林 132022；2.吉林石化公司 电石厂，吉林 吉林 132022)

板球装置作为球杆系统的二维扩展，是一类高阶、不确定性非线性系统,对其研究涉及动力学建模、伺服系统设计、轨迹跟踪等众多领域[1].小球运动过程中，板和球之间的非线性摩擦力、模型误差、执行机构的滞后现象等因素都会降低轨迹跟踪精度，导致控制效果不佳.国内外学者研究了模糊控制[2]、滑模变结构控制[3]、神经网络控制[4]、预测控制[5]等相关算法以获得期望的控制性能.吉林大学的段慧达博士针对板球系统可能出现的量测噪声污染问题，研究了带滤波功能的自抗扰设计方案，并提出了基于RBF神经网络的自抗扰控制器参数优化方法，最后利用级联自抗扰控制器较好地实现了轨迹跟踪控制[6].北京理工大学董振晔针对系统采集小球位置存在量测噪声这一问题，设计了含一阶惯性环节的扩张状态观测器，同时用自抗扰控制器实现了小球在不同速度下的定点控制和轨迹跟踪控制[7].

本文综合考虑板球系统的摩擦、扰动等不确定因素以及系统耦合项对小球轨迹跟踪精度的影响，利用扩张状态观测器对其进行估计和“补偿”，完成自抗扰控制方案的设计.由于板球系统实验平台X、Y轴的输入信号存在量测噪声干扰，故采用全程快速微分器滤除干扰，同时提取输入信号并求导，实现无需速度测量的控制，且全程快速微分器与跟踪微分器TD相比，受参数影响小、计算更为简洁.接着设计高阶扩张状态观测器ESO观测小球的位移、速度、角度、角速度状态变量，将观测出的系统状态变量与反步法相结合，设计出高阶自抗扰控制器.其中，ESO参数的选择至关重要，低阶次ESO的参数一般采用与步长幂函数的倒数成正比的规律选取.而本文设计的高阶次ESO的参数，采用步长与菲波娜奇数列的规律选取.仿真结果表明，与级联自抗扰控制器相比，改进的高阶自抗扰控制器设计结构简单、计算方便，有效地降低了板球系统的不确定扰动影响，轨迹跟踪效果更为理想.

1 板球系统建模

板球系统实验平台如图1所示.

图1 板球系统实验平台

主要由两个步进电机及相关驱动系统、平板、小球、视觉系统等组成.板球系统具有4个自由变量，即小球的位置(x,y)和平板X、Y轴的转动角度.通过欧拉-拉格朗日方程推导后，板球系统的状态空间模型为[8]：

(1)

y=[x1,x5]T.

其中，x1、x2、x3、x4和x5、x6、x7、x8分别为板球系统X、Y轴的小球位移、速度和平板转动角度、角速度.u0x和u0y为系统的控制输入(物理意义为角加速度).k=m/(m+Jb/r2)，m为小球的质量，r为小球半径，Jb为小球转动惯量，Jb=2mr2/5.y为板球系统的输出，即小球X,Y轴方向的位移.当小球在平板上运动时(无跳动现象)，平板的转动角度足够小(一般不超过±5°)可以忽略耦合项x4x5x8和x1x4x8.板球系统线性化、解耦后，可得X、Y轴线性子系统：

(2)

y1=x1,y2=x5.

2 自抗扰控制器设计

自抗扰控制器由跟踪微分器(TD)、非线性反馈控制器(NLSEF)、扩张状态观测器(ESO)3部分组成.因板球系统X、Y轴对称分布，故控制器的推导以X轴为例，Y轴控制器的推导参考X轴即可.本文的跟踪微分器采用全程快速微分器实现信号的提取和求导[9].

2.1 全程快速微分器

韩京清教授设计的非线性跟踪微分器，能够快速、精准地安排过渡过程并提取其微分信号，同样适用于多种控制系统.但在信号的跟踪过程中具有抖振现象，影响系统的轨迹跟踪精度.全程快速微分器采用非线性和线性组合的连续函数形式，能够对系统输入信号准确的求导，防止出现抖振现象，同时对输入信号的测量误差和输入噪声具有鲁棒性.

(3)

y3=z2(t).

(4)

y3=z2(t).

2.2 扩张状态观测器

板球模型中的不确定扰动和摩擦力对系统的响应造成较大的干扰，为获得更加准确的跟踪轨迹，设计扩张状态观测器时将这部分扰动作为总扰动进行估计补偿.根据板球系统模型式(2),设计完整的四阶板球系统中X轴子系统对应的扩张状态观测器.

定义轨迹跟踪误差：

e1=x1-y0x,

(5)

(6)

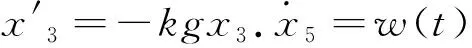
(7)

选择合适的β01、β02、β03、β04、β05估计板球系统的状态变量x1、x2、x3、x4和被扩张状态的实时作用量w(t).为避免小球运动过程中出现高频颤振现象，将扩张状态观测器中函数|e1|αsign(e1)改造成原点附近具有线性段的连续的幂次函数[10].

(8)

函数fal(·)具有小误差、大增益，大误差、小增益的非线性特点.由于δ通常取值为小于1的数，β0i通常取值为大于1的数，而β0i的选取决定了ESO对扰动的观测精度，进而影响轨迹跟踪精度.低阶ESO中的β0i参数值的选取一般采用β0i与1/hi(h=δ)成正比的规律[7,10].本文ESO式(11)β0i参数值的选取采用文献[10]中式(4.8.3)菲波娜奇数列与h(h=δ)的关系进行选择.

(9)

2.3 非线性反馈控制器

在板球系统的控制器设计中实现“模型和未知外扰补偿”是非常重要的.本文的非线性反馈控制器采用反步法，以Lyapunov函数的收敛性为目标，将完整的板球系统逐步分成若干个子系统.通过对后面的每一个子系统逐步引入虚拟函数，使前面的若干子系统满足Lyapunov稳定性，最终完成整个板球系统控制规律的求解，实现系统的全局调节，达到理想的控制效果.

结合式(2)、(5)定义系统偏差[1]：

(10)

其中，α1、α2、α3为虚拟函数.选取Lyapunov函数V1：

(11)

结合式(10)，对式(11)求导后可得：

(12)

设α1=-c1e1(c1>0的常数)，结合式(10)可求得：

(13)

(14)

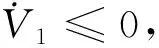
选取Lyapunov函数V2：

(15)

(16)

(17)

(18)

选取Lyapunov函数V3：

(19)

结合式(18),对式(19)求导后可得：

(20)

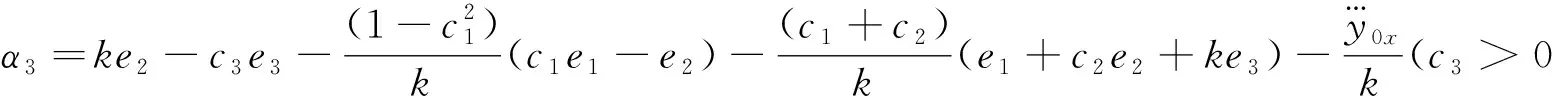
(21)

(22)

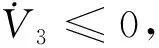
选取Lyapunov函数V4：

(23)

结合式(10)、(13)、(17)、(21)、(22)和α3，对式(23)求导后可得：

(24)

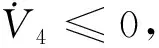
(25)

其中c4>0的常数.

化简后可得：

(26)

综上可知，完整的四阶板球系统X轴自抗扰控制器由式(4)、(7)、(26)组成.

3 仿真结果分析

x1/m图2 高阶自抗扰控制轨迹跟踪

在零初始条件下，板球系统X、Y轴输入信号处加入幅值为0.01的随机信号作为噪声干扰.m=0.1 kg，r=0.01 m，g=9.8 m/s2，k=5/7，c1=4，c2=3，c3=2,c4=1，b=-7.007.式(4)中R=20，a0=b0=0.1，v(t)=y0x.式(7)中δ=0.375，β01=2.67，β02=2.373，β03=0.594 8，β04=0.043 32，β05=0.005 582.板球系统Y轴自抗扰控制器设计参照X轴即可.当系统稳定运行时，外界扰动wx和wy选择step=0.5的阶跃输入.小球从原点(0,0)出发，做R0=0.1 m圆形轨迹跟踪运动.输入信号如下：

(27)

仿真实验在Matlab2014环境中进行，自抗扰控制器各部分模型采用S函数进行封装，分别设计级联自抗扰控制器和高阶自抗扰控制器，在Simulink中分别搭建系统仿真模型.图2～6给出了高阶自抗扰控制的仿真结果.作为对比，图7～10给出了级联自抗扰控制的仿真结果.对比图4和图9可知，高阶自抗扰控制5 s内能够迅速跟踪预设轨迹，而级联自抗扰控制20 s后才趋于稳定；另外高阶自抗扰控制X、Y轴误差的绝对值分别是5.45和4.925 mm,而级联自抗扰控制X、Y轴误差的绝对值分别是6.5、13.25 mm，控制精度显著提高.对比图5和图10，高阶扩张状态观测X、Y轴扰动几乎为零，达到了理想的干扰抑制效果，而级联自抗扰控制的干扰抑制效果欠佳.高阶自抗扰控制和级联自抗扰控制中的全程快速微分器X、Y轴输出图仿真结果相同，均能有效地滤除输入信号干扰，故只给出高阶自抗扰控制中的全程快速微分器X、Y轴输出曲线，如图6所示.

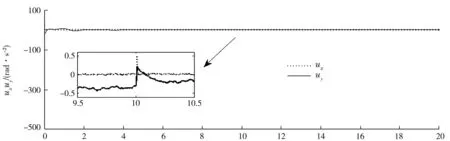
t/s图3 高阶自抗扰控制器X、Y轴输出

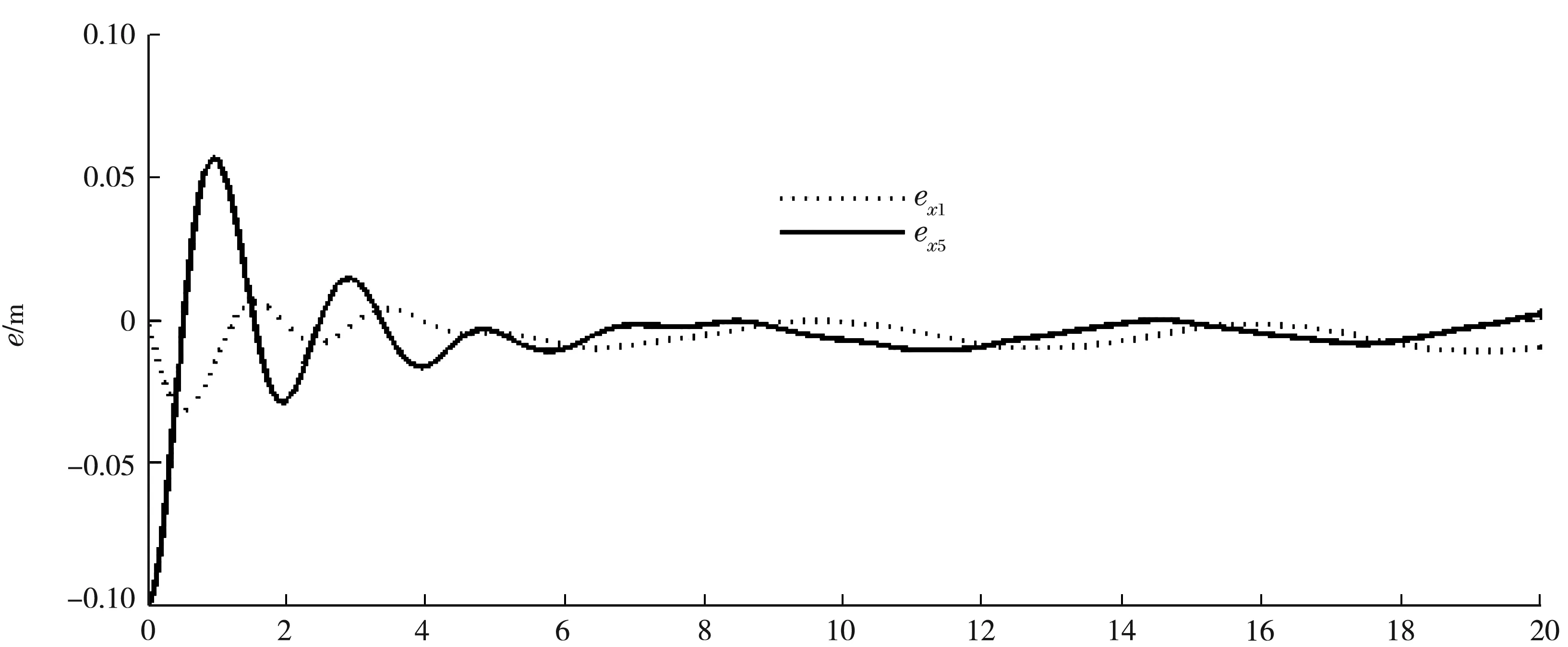
t/s图4 高阶自抗扰控制X、Y轴误差

图5 高阶扩张状态观测X、Y轴扰动

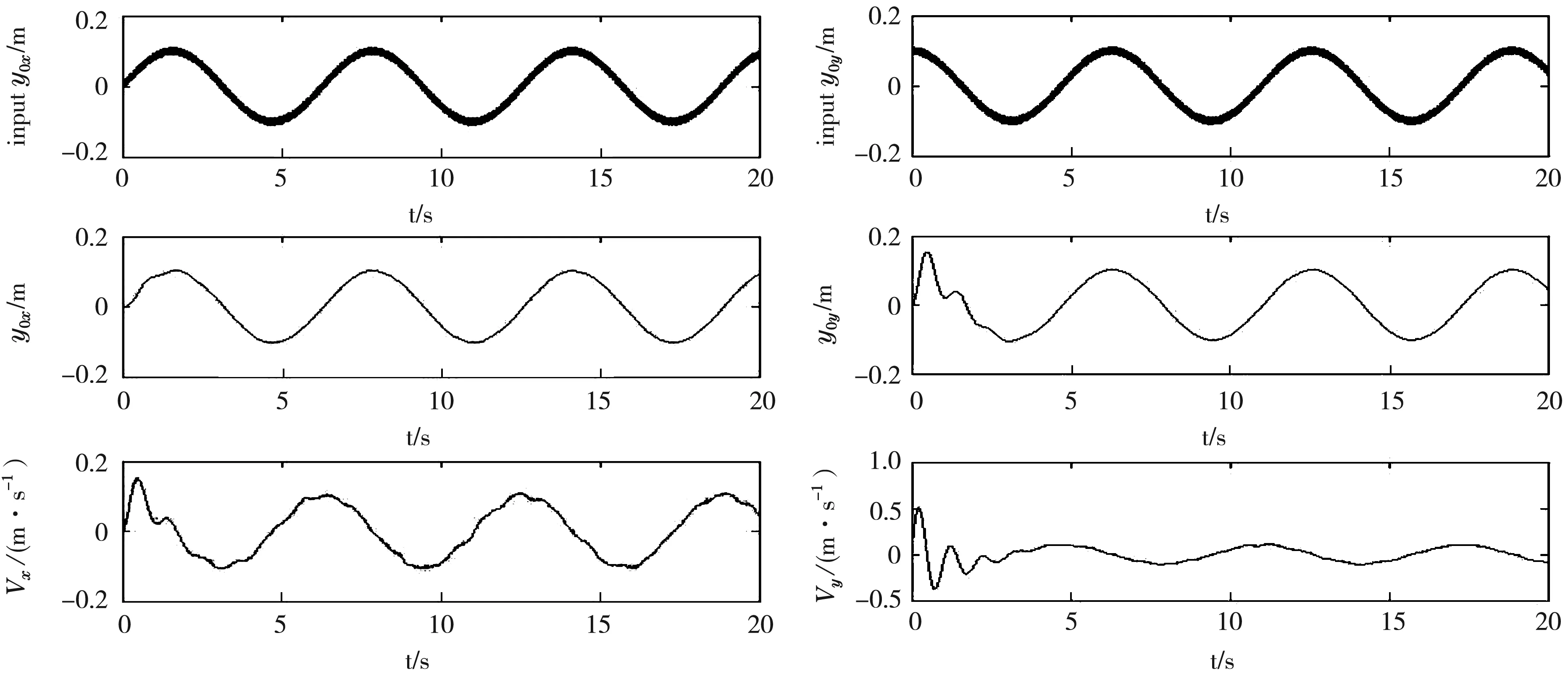
图6 高阶全程快速微分器X、Y轴输出

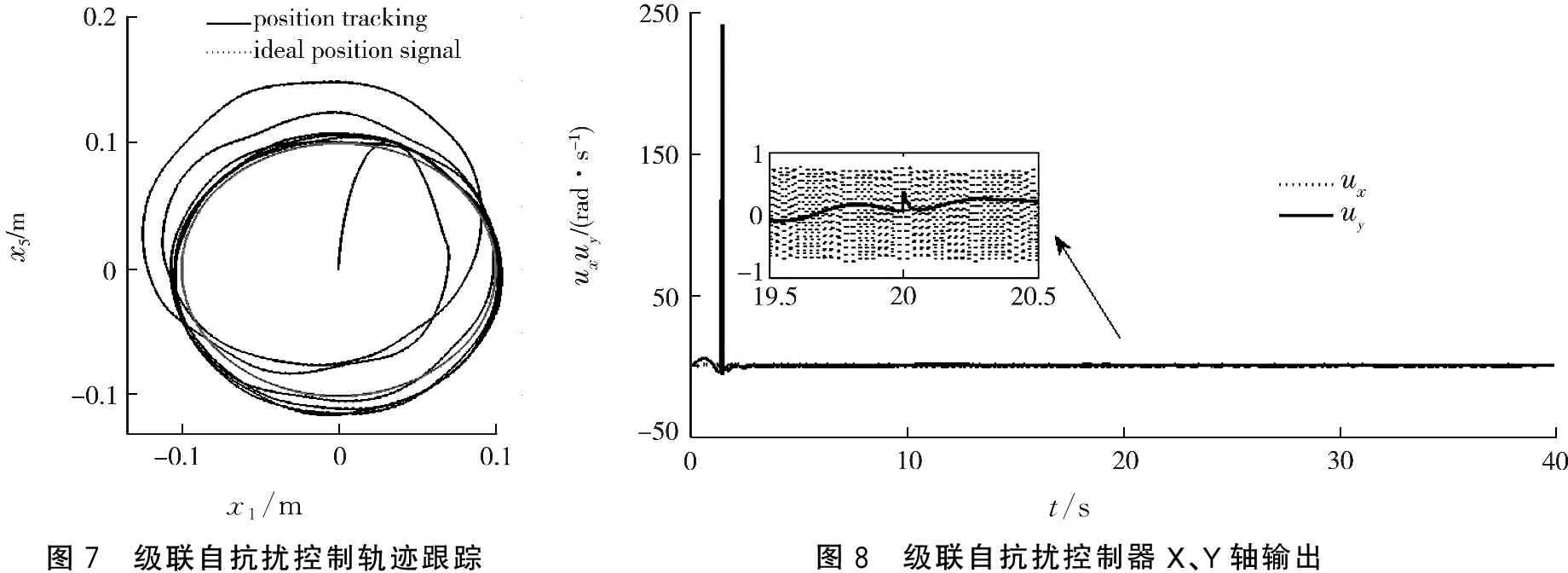
x1/m图7 级联自抗扰控制轨迹跟踪t/s图8 级联自抗扰控制器X、Y轴输出

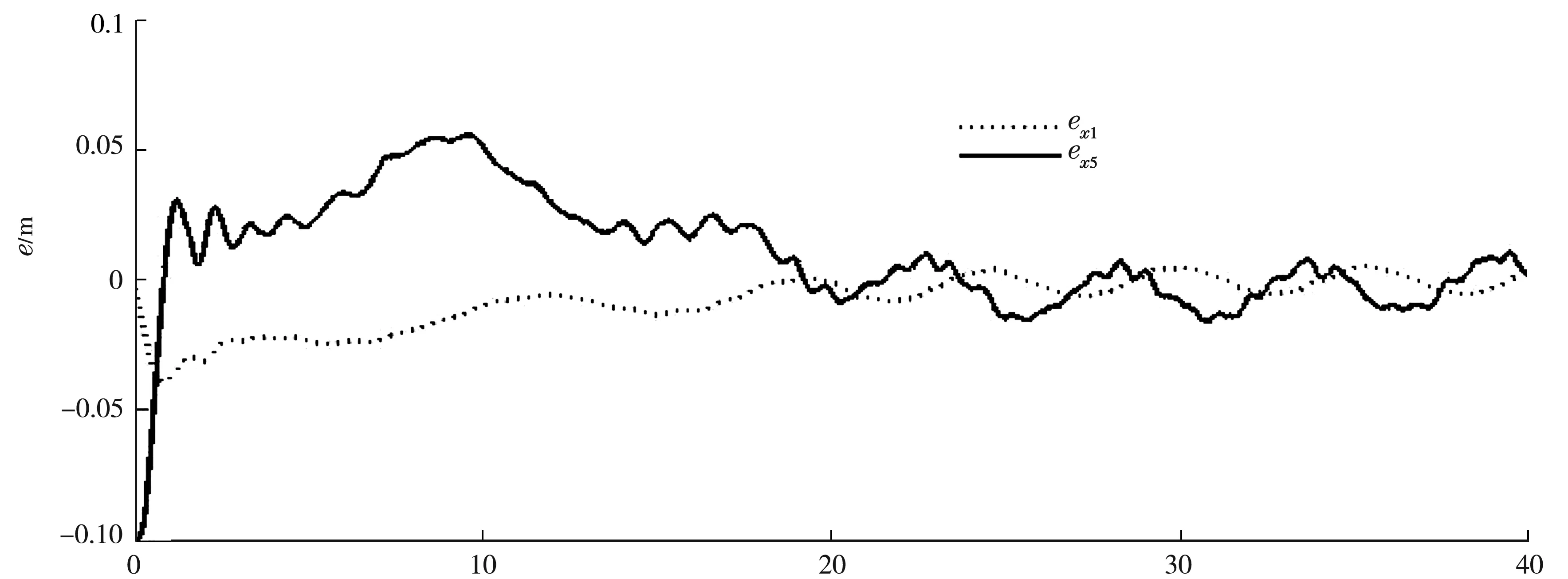
t/s图9 级联自抗扰控制X、Y轴误差

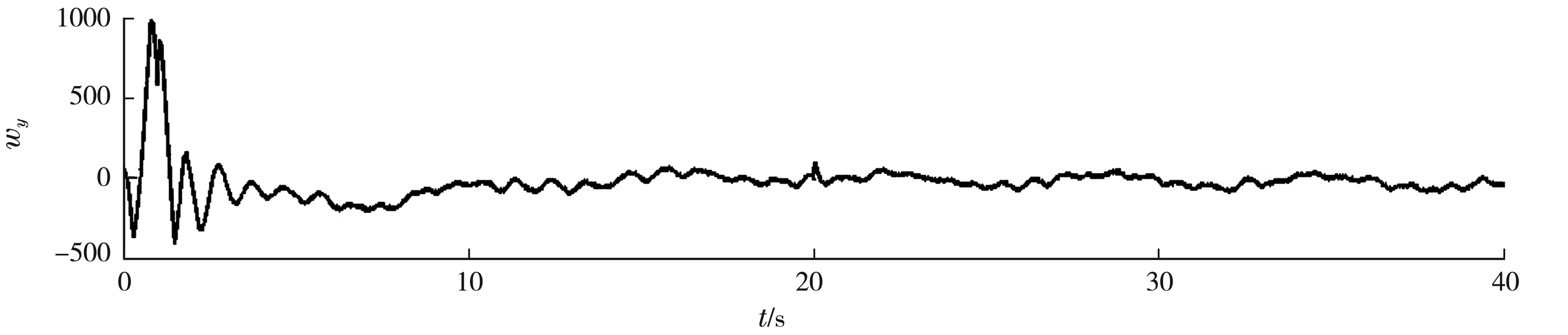
图10 级联扩张状态观测器X、Y轴总扰动

4 结 论

以多变量、强耦合的板球系统作为研究对象，针对系统受到的内、外部不确定干扰而影响轨迹跟踪精度这一问题，在设计自抗扰控制方案中，采用全程快速微分器滤除系统输入信号的噪声干扰，利用ESO实现对板球系统内部干扰的估计和“补偿”，并将观测的状态变量与非线性反馈控制器的设计相结合，设计出高阶次的自抗扰控制器.实验结果表明，高阶次的自抗扰控制器克服自身和外部的干扰能力强，能够快速实现高精准的轨迹跟踪控制.