基于SVR-GA的燃煤锅炉NOx含量软测量研究

孙 悦，王雪晶，于 攀，曹玉波*

(1.吉林化工学院 信息与控制工程学院,吉林 吉林 132022；2.吉林石化公司 合成树脂厂，吉林 吉林 132021；3.科世达汽车电器有限公司 AP1工艺工程部,吉林 长春130033)

随着工业生产活动的增加，氮氧化物(NOx)排放对大气环境的破坏并影响人类健康的问题也越来越受到广大专家学者的重视.其中燃煤锅炉是NOx的主要排放源之一，对燃烧废气中NOx含量进行实时和准确测量是控制和减少污染排放的首要环节.然而，传统的借助仪器直接测量的方法存在测量精度低、实时性差的问题.而软测量方法是建立NOx排放的预测模型进行预测，具有方便使用、精度高的优点，目前已经有学者从不同角度对软测量预测模型进行了研究[1-2].

支持向量机是一种由Vapnik提出的统计学习方法[3].理论基础已经十分完善，并且数学模型简洁明了.由于现场工况复杂多变，常规的软测量方法建立的模型固定且单一，变负荷运行时存在预测精度不稳定、泛化性差的问题.本文采用支持向量回归算法建立锅炉的NOx排放软测量模型，并利用遗传算法(GA)良好的寻优特性选取最佳的模型参数以提高模型预测精度.同时为验证模型预测性能，将GA-SVR模型与SVR、BPNN等模型进行对比分析.最终实验结果表明，GA-SVR所建立的模型具有最佳的预测精度和泛化能力，可以有效解决脱硝反应器入口NOx排放量难以精准测量的问题，为燃煤电厂后续进一步做燃烧优化提供参考.

1 算法简介

支持向量机主要优点表现在克服了模型过拟合同时保留了良好的泛化能力.回归问题可理解为：

根据输入输出数据集(xi,yi)(i=1,2,3,…m)，求取一个超平面：f(x)=wx+b.

在支持向量回归中，先将输入向量映射到高维特征空间，然后，在高维空间中构造优化超平面：

f(x)=wTxg(x)+b，

(1)

式中，W是权重向量；g(x)是将x映射到特征空间的映射函数；b为偏置.设φ(x)为映射用的非线性函数，则k(xi,xj)=φ(xi)·φ(xj)，称为核函数.

(2)

约束条件为：

(3)

利用支持向量回归机建立锅炉燃烧NOx预测模型，选用径向基函数[exp(σ×|xi-xj|2)]作为核函数，其中各项参数可以通过遗传算法优化获取最优参数组合[5].

遗传算法[6]是一种以自然选择学说为基础的并行随机搜索最优化方法.通过选择交叉变异的方式实现群体的循环迭代以达到参数优化的目的.凭借着精度高、搜索更加灵活的优点，使得遗传算法具有了广泛的应用领域，如函数优化[7]、自动控制[8-9]、图像处理[10]、机器学习[11]、数据挖掘[12]等领域.

2 基于GA的支持向量回归算法

2.1 适应度函数和评价指标

群体中每个个体都有Ci和gi两个参数，遗传算法迭代的目的在于寻找使得模型均方误差和最小的参数组合，为了方便计算，因此选择均方误差(MSE)为适应度函数，第i个个体的适应度为：

(4)

为了对模型预测结果进行比较，本文采用平均绝对误差(MAE)，平均相对误差(MRE)和均方根误差(RMSE)3种指标来评价模型的预测能力.计算方法如式(5)～(7)所示.

(5)

(6)

(7)

2.2 算法步骤

基于GA算法的支持向量回归算法步骤如下：

通过迭代得到最优的参数组，并对支持向量回归模型进行训练.

GA-SVR支持向量回归模型流程如图1所示.

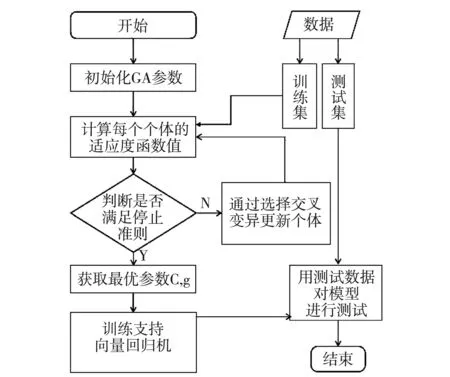
图1 GA-SVR建模和寻优流程图

3 NOx排放响应模型建立及验证

本次研究使用的数据来自国内某发电公司300MW亚临界固态排渣锅炉.锅炉采用同心反切燃烧系统，炉膛的四角布置有切向摆动式燃烧器，可控制摆动以调节再热汽温，同时配有5层一次风门、6层二次风门以及顶端燃尽风门.

锅炉燃烧系统主要生产过程分为燃料传送、燃烧、废气排放3个部分.原煤通过传送带送至磨煤机内，在磨煤系统中被磨成煤粉，同时送入经过空气预热器的热一次风和经过送风机的冷一次风，再将煤粉和二次热风混合送入炉膛燃烧室，其中二次热风提供煤粉燃烧所需要的氧气，煤粉燃烧所释放的能量经过蒸汽系统产生饱和蒸汽，送至涡轮汽缸驱动发电机发电.与此同时，燃烧过程中产生的氮氧化物废气通过排风机从烟囱排出.

3.1 输入参数选取

对于该300MW燃煤锅炉，总燃料量和总空气量这两个参数用以描述锅炉运行负荷对NOx排放的影响；5层一次风门、6层二次风门以及燃尽风门挡板开度用以描述不同的配风方式对NOx排放的影响；烟气含氧量描述排出气体的含氧量对NOx排放特性的影响，以及不可控参数煤质特性，这些参数都对NOx排放有着较大的影响.

结合实际工业流程以及对NOx生成机理的分析，选取以下27个变量作为输入参数：总燃料量、总空气量、一次风门开度(5项)、二次风门开度(6项)、烟气含氧量、煤质参数(6项)、给粉机通风量(5项)、OFA风门开度(2项)，选取NOx排放量为输出参数，通过DCS现场数据采集系统，采样周期1 min，共计采集NOx排放相关参数变量运行数据1 000组.其中主要变量信息如表1所示.

表1 主要变量信息

3.2 GA-SVR预测模型的建立

利用Matlab软件为仿真平台编制程序，以现场采集的1 000组工况数据为基础，选取其中800组用于训练样本，剩余200组用于预测，训练样本分别用于对GA-SVR、BP神经网络模型、常规SVR模型进行训练.

BP神经网络采用了27-25-1的网络结构，每层的激活函数采用tansig函数，迭代次数为500；GA-SVR模型，种群数为50，最大迭代次数为50，参数寻优的设定范围C∈[0.01,500],g∈[0.01,50].遗传算法参数优化的效果图如图2所示，从图中可知，使用GA算法对模型的参数g和C进行参数寻优，并且10折交叉验证下最优的适应度为17.779 3，此刻的最优参数组合g为0.188 1，C为51.227 7.

进化代数图2 GA参数寻优适应度变化图

图3中(a)展示了3种不同的模型对800组训练样本的预测误差图，(b)为3种不同模型对200组测试样本的预测误差图.由图3(a)中可以看出，在训练样本中SVR模型和GA-SVR模型的效果最佳，相对误差绝大部分处于区间(0，0.25].不过在图3(b)测试样本的预测中，经过遗传算法调参的SVR模型明显优于其余两者，调参之后的模型泛化能力更强.

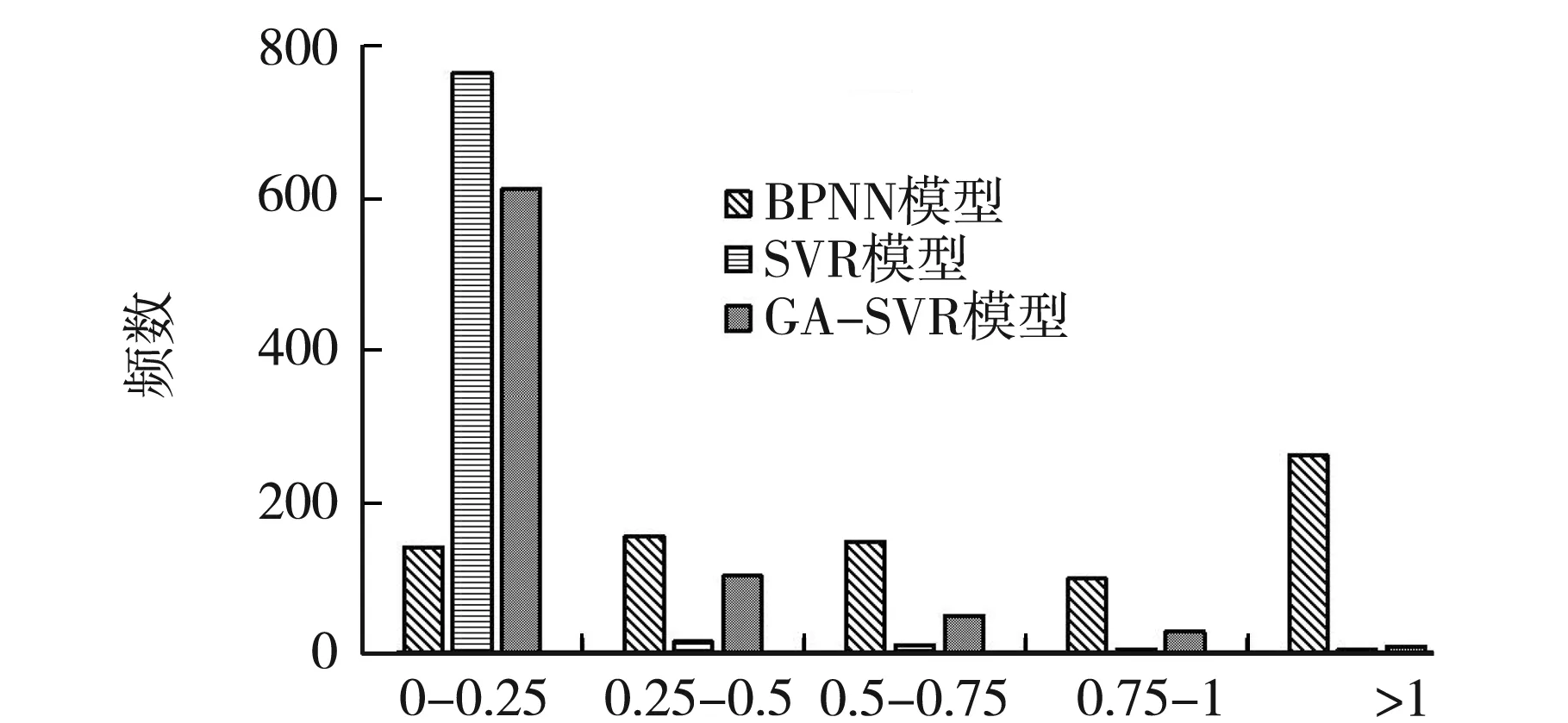
相对误差/%(a)训练样本误差图

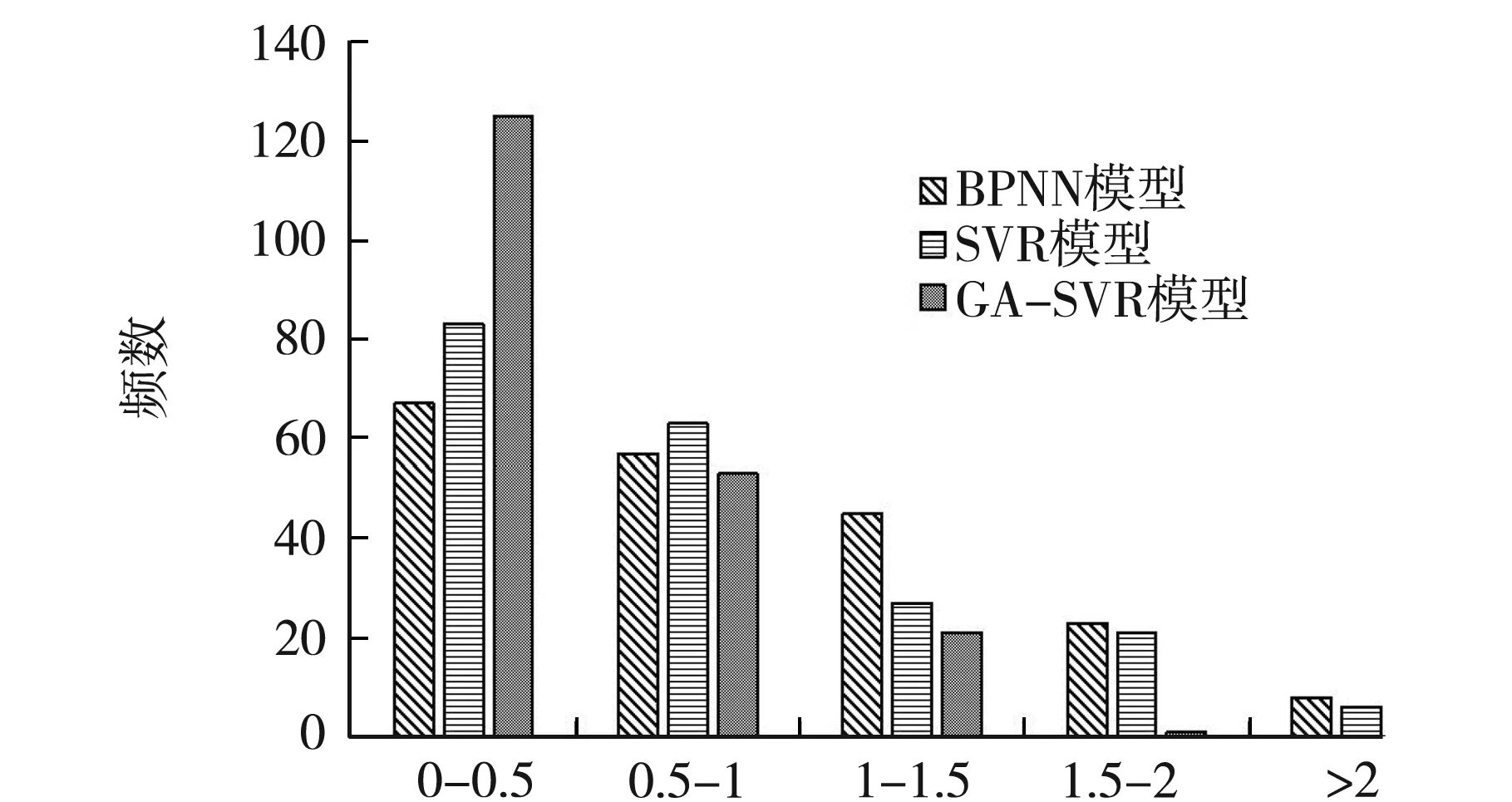
相对误差/%(b)测试样本误差图图3 NOx排放量预测误差图

3.3 实验结果分析

图4(a)～(c)为3种模型下200组测试样本的预测结果散点图.

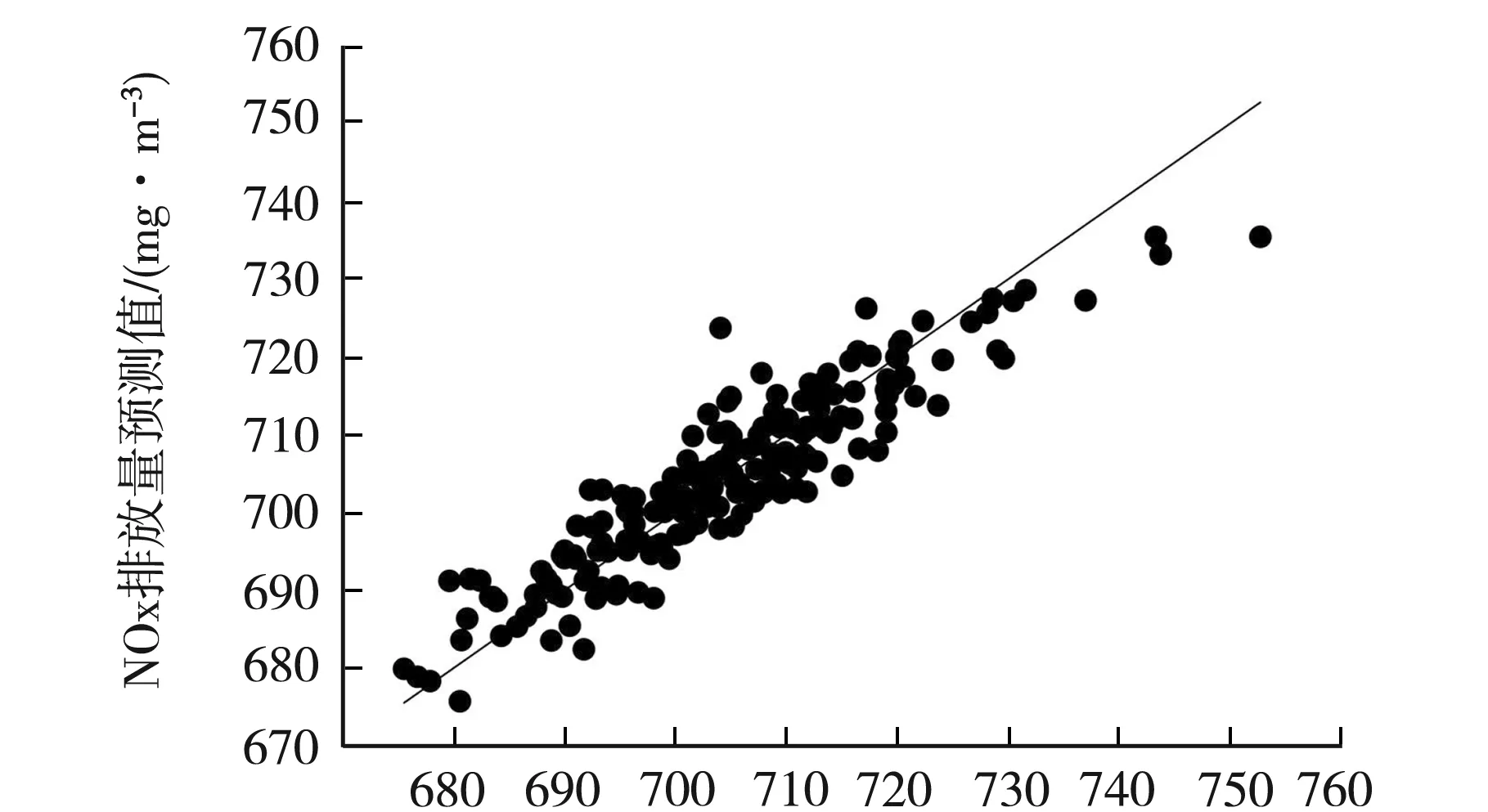
NOx排放量实际值/(mg·m-3)(a)BPNN模型预测结果

NOx排放量实际值/(mg·m-3)(b) SVR模型预测结果

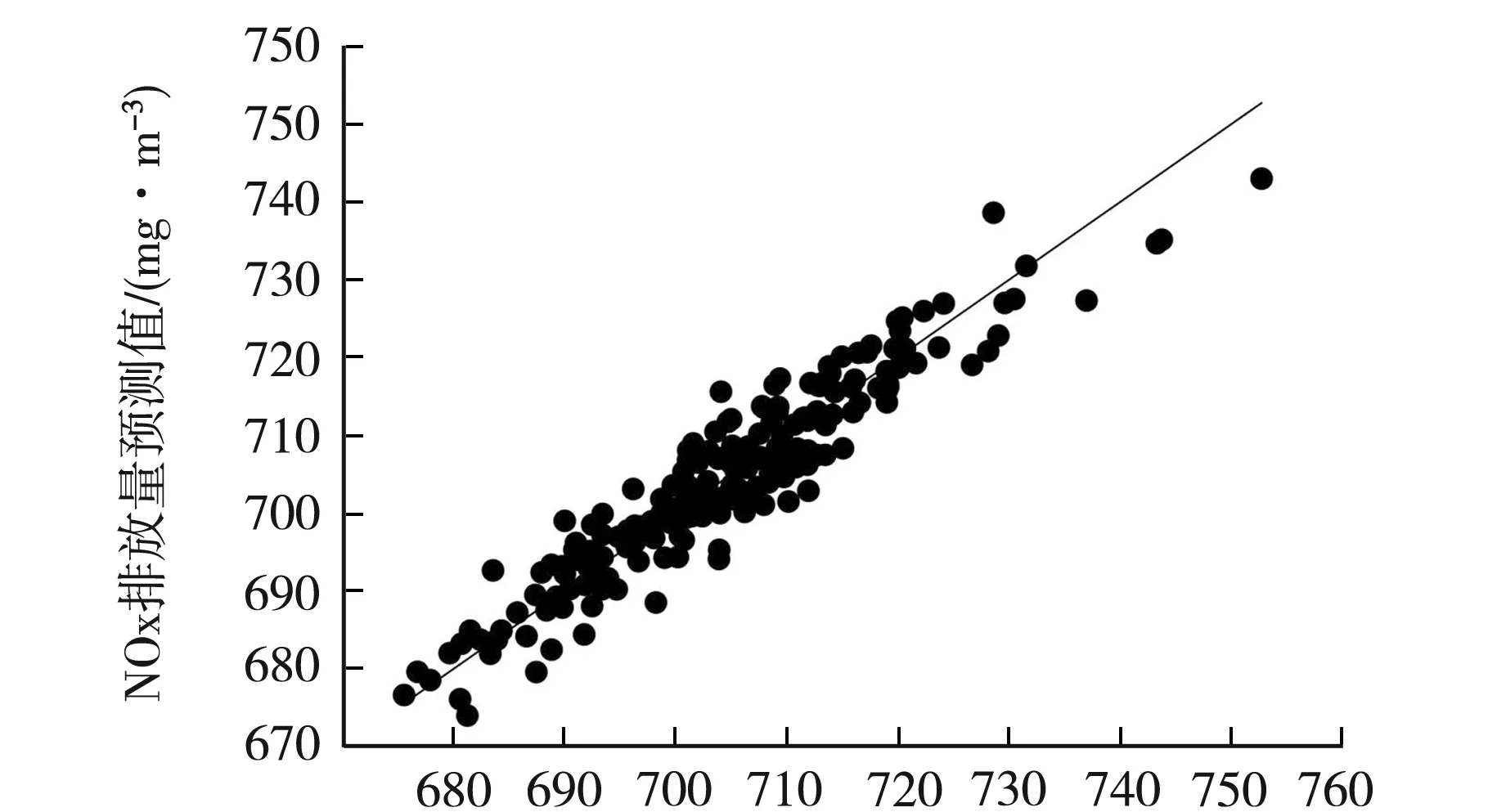
NOx排放量实际值/(mg·m-3)(c) GA-SVR模型预测效果图4 测试样本预测效果图

GA-SVR模型无论是对训练样本还是测试样本都有较好的效果，体现出了GA-SVR模型较好的泛化能力，满足建模的要求.

根据上面建模过程中获得数据，计算实验中SVR模型、BP神经网络模型、GA-SVR模型的训练样本预测均方根误差(RMSE)分别为1.723 9，4.178 3，2.214 5，测试样本预测均方根误差(RMSE)分别为4.703 9，5.039 8，4.216 5.可见GA-SVR模型在训练样本上效果逊于SVR模型，不过其泛化性能更佳，且绝对误差都保持在2%之内，预测效果较好.表2为不同模型在测试集上的预测效果.由表2可以看出，GA-SVR模型的预测误差要好过BP神经网络模型和SVR模型，样本相对误差平均值为0.47%，可见GA-SVR模型的预测精度最高.

表2 不同模型预测结果对比

4 结 论

电厂燃煤锅炉NOx排放量的预测受多方面影响，传统的直接测量方法存在诸多问题且实时性差.针对这些问题，本文使用支持向量回归算法建立NOx排放的软测量预测模型.并结合GA算法对SVR模型参数进行优化，使用电厂DCS数据采集系统中获取的现场数据对GA-SVR模型进行验证，并与常规SVR模型、BP模型进行了对比分析.实际结果表明，GA-SVR模型精确度更高，泛化能力更好.可以实现对电厂锅炉NOx排放量的精准预测，后续可以结合全局优化算法，搜寻出最优的操作参数组合，为大型电厂锅炉通过燃烧降低NOx排放提供有效手段.