电励磁直线同步电机磁悬浮系统自抗扰控制*

李 枫, 蓝益鹏

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

0 引 言

数控机床直线电机直接驱动系统，与传统驱动系统不同，省掉了中间传动环节，具有运动惯量小，结构简单，高精度和高速度等优点。但是运动部件与导轨之间的摩擦问题依然存在，影响直线伺服系统的性能，为了解决这个问题采用磁悬浮电励磁直线同步电机(EELSM)，消除摩擦对系统的影响，从根本上改善系统的性能[1-3]。EELSM水平方向上产生电磁推力驱动平台直线运动，垂直方向产生可控悬浮力使平台悬浮于导轨上，实现无摩擦进给[4]。由于EELSM系统省掉了中间传动环节，端部效应等不确定扰动会直接作用在直线电机上，对系统性能影响更加显著，控制变得困难。因此，如何选择合适的控制方法提高系统的鲁棒性受到广泛关注。

目前，直线电机控制系统中，PI控制器仍然占有主要地位，其原理是“基于误差反馈来消除误差”。针对PI控制存在“快速性”和“超调”的矛盾问题，1998年韩京清[5]提出自抗扰控制(ADRC)。多年来对ADRC研究已取得丰硕的成果。文献[6]针对线性扩张状态观测器的估计能力和闭环系统的稳定性问题分析，论证构造出适合的线性扩张观测器可使估计误差趋于零。文献[7-8]从频域分析方法入手，基于频带特性曲线，提出一种新的非线性ADRC参数整定公式，简化了非线性扩张观测器参数整定。文献[9]对ADRC的原理进行系统性地理论分析，进一步论证参数对系统稳定性及性能的影响，阐述了ADRC所蕴含的思想。文献[10-11]设计速度环ADRC，通过试验证明当负载变化时，电机转速仍可以稳定。文献[12]提出一种二阶NLADRC实现位置和速度的复合控制，简化了伺服系统的调试过程且提高了系统动态响应速度。

综上所述，NLADRC具有更高的控制精度和更强的抗扰能力，其控制效果与非线性函数选取、参数调整大小有直接关系。本文针对EELSM数学模型的特点，设计了三阶NLADRC，并对其抗扰原理进行研究。通过对比和分析非线性函数参数变化对系统性能的影响，归纳和揭示出参数的物理意义及其整定方向。最后通过仿真表明，本文所提出的三阶NLADRC控制对EELSM悬浮系统有很好地抑制非线性因素和内外扰动的效果。

1 构建EELSM磁悬浮系统数学模型

1.1 EELSM磁悬浮进给平台构成

本文选取EELSM磁悬浮进给平台如图1所示，由EELSM、平台基座、辅助导轨、电涡流传感器、运动平台、光栅尺组成。

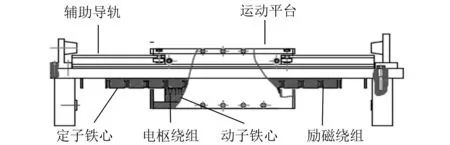
图1 EELSM磁悬浮进给平台结构图

EELSM悬浮系统驱动原理：电枢绕组通入三相电流，会在气隙中产生水平方向的行波磁场。励磁绕组中通入直流电流，会在气隙中产生励磁磁场。行波磁场与励磁磁场相互作用产生电磁推力，推动平台直线运动。垂直方向上，励磁磁场与动子铁心之间产生磁悬浮力与悬浮平台重力相等时，实现平台稳定悬浮[13]。根据此原理推导出垂直方向的状态方程。

1.2 EELSM磁悬浮系统状态方程

EELSM磁悬浮系统在dq轴系下的数学模型[14]如下。

电压方程：

(1)

(2)

(3)

式中：ud、uq、id、iq为dq轴系下的电压与电流；uf与if为励磁电压和励磁电流；Rs与Rf为推力绕组的电阻和励磁绕组；τ为电机的极距；v为电机运行速度。

磁链方程：

ψd=id(Lmd+Lσ)+ifLmd

(4)

ψq=iq(Lmq+Lσ)

(5)

ψf=if(Lmd+Lσf)+idLmd

(6)

式中：ψd、ψq为dq轴系下的磁链；ψf为励磁磁链；Lmd、Lmq为d、q轴主电感；Lσ为推力绕组的漏电感；Lσf为励磁绕组的漏电感。

采用id=0的矢量控制方式，得到电机的悬浮力方程:

(7)

式中：Z为悬浮高度。

(8)

式中：Fy1是Fy中第2项当作扰动处理后的磁悬浮力。

悬浮方向的运动方程：

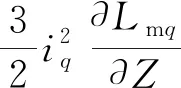
(10)

式中：k为磁悬浮系数，数值为5.659×10-6。

以此完成数学模型构建，将其中不确定性因素视为扰动处理。

2 EELSM磁悬浮ADRC控制器设计

2.1 EELSM磁悬浮ADRC结构

针对EELSM系统存在非线性以及不确定性扰动的特点，本文采用三阶NLADRC控制器，控制其悬浮高度，所采用标准型为串联积分型(并非实际结构)。总扰动除了包括实际结构与标准型结构的差别外，还包括系统中不确定因素以及内外扰动[15]。图2为本文设计的基于NLADRC控制的EELSM悬浮系统原理框图。虚线框内为三阶NLADRC控制器，分别由跟踪微分器(TD)、扩张状态观测器(ESO)以及非线性状态误差反馈控制律(NLSEF)组成。

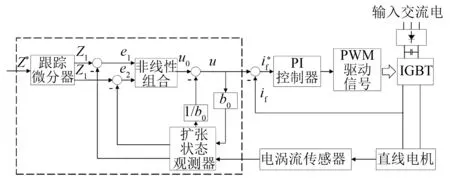
图2 EELSM磁悬浮ADRC结构图

2.2 跟踪微分器设计

对于初始状态，误差过大会导致控制量过大进而对系统有冲击影响，可以利用TD在系统输入前安排过度过程，消除超调的同时保证快速性，并且给出输入给定值的近似微分信号。

根据推导出状态方程选取最速跟踪微分器表达式为

(11)

式(11)非线性TD采用的fhan函数形式。其表达式如下：

式中：e为输入信号与跟踪信号的误差；h为采样周期；参数r为决定跟踪速度的因子。

为了消除进入稳态时出现超调现象，将最速跟踪微分器fhan(e,x2,r,h)函数中的h换成h0，只要取h0为适当大于h的参数就会消除超调现象[16]。

通过仿真实验可知，h0的大小影响跟踪微分器的响应快慢，当参数r不变时，改变h0大小来跟踪响应快慢的变化，如图3所示。

图3 h0不同时跟踪曲线

由图3可知，给定值为2.5×10-3m时，不同的h0过度时间不同，当h0为2、3、4时，过度时间分别为0.517、0.839、1.122 s，由此可见h0值越小响应速度越快。

2.3 非线性扩张状态观测器设计

非线性ESO通过对系统输入量与输出量测量进而确定内部各状态量，测出系统被施加的总扰动，再通过控制器进行扰动补偿，使系统稳定。

要实现我国山区玉米的高产栽培，首先需要对玉米种子和山区种植的基础设施进行完善，充分结合山区的气候因素和环境因素，选择合适的种子进行推广，需要注意的是，即使是同一个地区的土壤也会存在着一定的差异，需要对种植区域的土壤等因素进行详细的分析，并针对性的采用科学的种植方法。例如可以采取轮作等方式来有效的提升玉米产量，同时不断的改良土壤，从而更好的提升农户的经济收入。

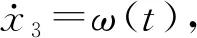
(13)

则对应的扩张状态观测器：

(14)

(15)

式中：α为幂次；δ为线性区间。fal函数在原点附近为线性的连续幂次函数。

在式(10)中g为已知重力加速度，为了观测未知扰动，需要将已知部分放进扩张状态观测器中。最终建立的悬浮方向上的三阶扩张状态观测器为

(16)

式中：β01、β02、β03、a、δ、b0为系统可调参数；z3为系统中被扩张的状态观测量。

2.4 非线性状态误差反馈控制律选取

式(17)中e1和e2是TD的输出与ESO的输出之间的误差，通过e1和e2计算误差反馈控制量u0，其中k1、k2为可调参数，然后通过ESO观测出总扰动进行补偿，得到最终的控制量u，实现被控对象的反馈线性化，得出NLSEF的数学模型：

(17)

3 非线性函数fal参数α与δ的整定

对式(15)作如下变换[18]：

(18)

此时fe(t)与fe1(t)是式λ(e)与误差e乘积。参数α与δ分别对系统有影响，两者之间又相互关联。分析δ的影响，当α=0.5时不同的δ值函数输出曲线如图4所示。

图4 δ不同时λ(e)函数变化曲线

由图4可知，当α=0.5时，δ越小其线性阶段越小，误差越小时函数λ(e)值就越大，但是δ取值过小，增益会过大造成系统不稳定。δ取值过大显示不出非线性的优势。因此，在实际应用中要根据具体的系统选取合适的线性区间，本文对EELSM悬浮系统验证，δ取值范围在0.000 1～0.005之间线性区间最好。

当α=0.5，δ=0.001时，λ(e)函数曲线如图5所示。

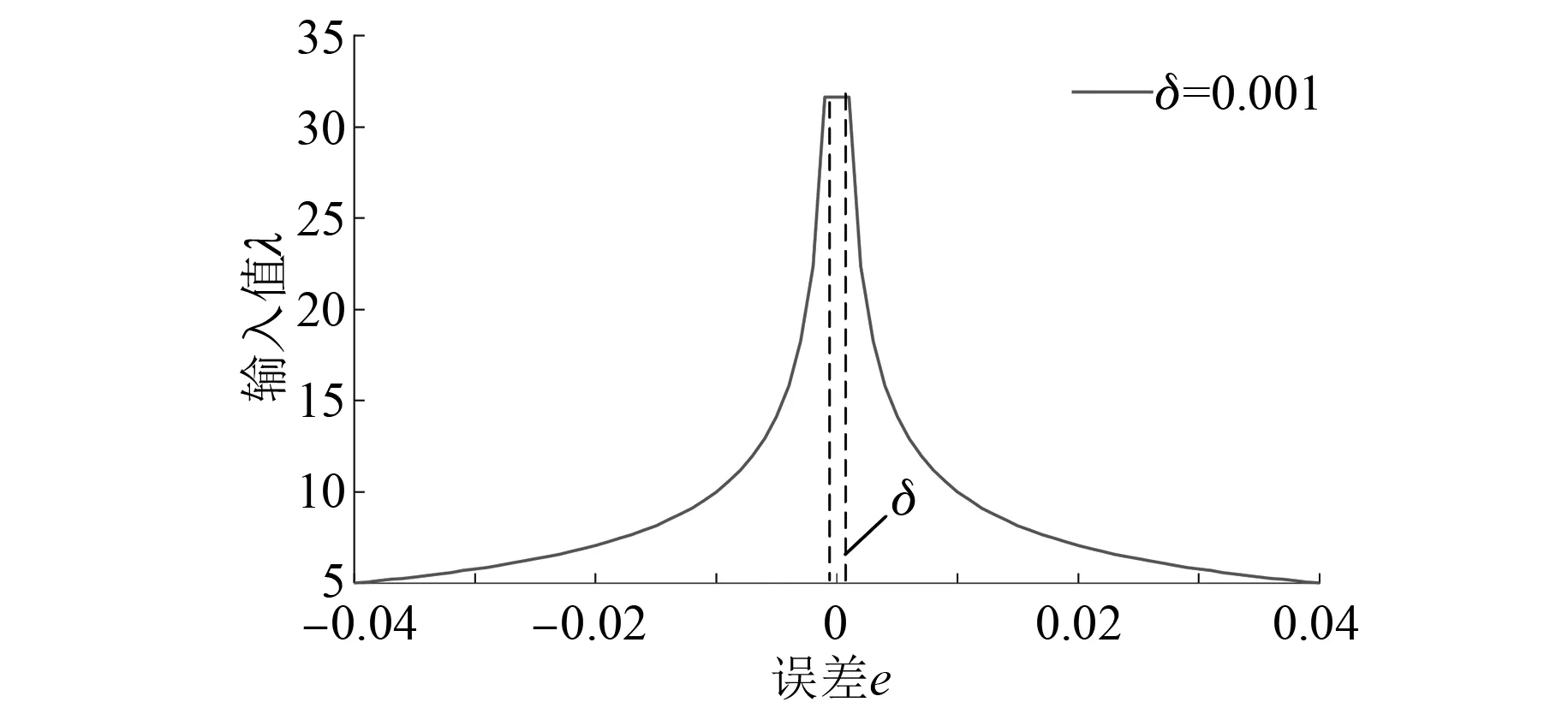
图5 λ(e)函数曲线

当误差值在δ区间内，函数输出为线性恒定值，此时表现为“小误差大增益”；当误差大于δ区间时，随着误差的增大增益逐渐减小，表现为“大误差小增益”。

α值同样影响系统性能，当δ=0.001时，不同的α值λ(e)函数曲线如图6所示。

图6 α不同时λ(e)函数变化曲线

由图6可知，α值越小，函数λ(e)的恒值越大，非线性的“大误差，小增益；小误差，大增益”特性越明显。但是当α取值过小会导致控制量高频振颤，取值过大会影响误差衰减性能以及抗扰能力。本文选择α为0.25和0.5。

4 仿真研究

由于ADRC需要整定的参数比较多，式(16)中控制增益b0整定可按照模型计算得出，也可试凑整定，已有研究表明总扰动中就包含控制增益b0的不确定性，b0也具有较强的鲁棒性，可大范围调节而不会引起系统的不稳定[8]。

本文通过模型计算得出b0=0.1。采用仿真试验得到β01=6 000,β02=200,β03=10 000,k1=20 000,k2=1 600。对控制系统进行计算机仿真，电流环采用PI控制，位置环采用NLADRC控制，与PI控制算法进行对比。

分3种情况对EELSM悬浮系统进行分析：

(1) EELSM的起动性能。图7为起动时PI控制与ADRC对比下悬浮气隙高度响应曲线。采用PI控制的系统，响应过程无超调，约0.12 s达到给定的磁悬浮气隙高度，但存在稳态误差，调节时间长。采用ADRC的系统，响应过程无超调，约0.053 s达到给定气隙高度，无稳态误差，调节时间短。因而ADRC控制比PI控制响应速度快，性能优越。

图7 起动时磁悬浮气隙高度响应曲线

(2) EELSM系统对负载扰动的抑制能力。系统稳定时，在0.3 s加上f=20 N的负载扰动，在0.6 s时卸掉负载。图8、图9分别是加入负载扰动后PI控制与ADRC对比下磁悬浮气隙高度响应曲线和励磁电流响应曲线。采用PI控制时，加入扰动后，动态降落为4.32×10-5m，恢复到给定值时间为0.2 s。采用ADRC系统动态降落为7×10-6m，恢复时间为0.05 s。说明ADRC的系统抗干扰能力强，对外界扰动不灵敏，在加入扰动后的稳态误差为0，反映了系统具有良好的扰动抑制能力。

图8 加入扰动时磁悬浮气隙高度响应曲线

图9 加入扰动时励磁电流响应曲线

(3) EELSM系统对直线电机特有端部效应的抑制能力。采用正弦函数f=15sin(20t)N模拟端部效应。图10为正弦扰动下的气隙高度响应曲线。采用PI控制时，加入正弦扰动后，波形波动剧烈抗干扰能力差。采用ADRC的系统没有明显的波动，抗扰能力优于PI。

图10 正弦扰动下磁悬浮气隙高度响应曲线

5 结 语

(1) 分析EELSM磁悬浮系统的结构以及运行机理，构建电压方程、运动方程，以及系统状态方程，将其中的不确定性因素视为扰动处理。

(2) 设计三阶NLADRC控制器。选取最速跟踪微分器，对给定信号进行跟踪滤波的同时给出微分信号，然后，通过构建的状态方程，设计三阶非线性扩张状态观测器，最后，构建出合适的非线性状态误差反馈律。分析NLADRC中的非线性函数fal的参数整定方向和规律。

(3) 通过对控制系统的计算机仿真，与PI控制器对比，三阶NLADRC应用于EELSM磁悬浮系统的抗扰性、稳定性和响应的快速性均具有明显优势。