地铁车辆永磁同步电机振动噪声测试及特性分析*

丁 杰, 尹 亮

(湖南文理学院 机械工程学院，湖南 常德 415000)

0 引 言

永磁同步电机具有功率密度大、效率高、过载能力强等特点，在轨道车辆中得到较多应用[1-3]。永磁同步电机工作过程中，由气隙磁场产生的电磁力驱动转子旋转的同时，也会使定子铁心振动而产生电磁噪声，影响乘坐的舒适性。因此，永磁同步电机的振动噪声问题受到了很多关注。

国内外学者从理论分析、仿真计算和试验测试等方面对电机的振动噪声问题开展了大量研究。Gieras等[4]对多相电机的噪声问题开展了系统性研究。韩雪岩等[5]基于电机电磁力时空阶次分析和气隙电磁力的时空分解，提出一种计算电机电磁振动噪声的准解析方法。付敏等[6]利用有限元分析与傅里叶分解方法，分析得出电机运行中出现的振动噪声问题主要由谐波分量引起。李晓华等[7]针对电动汽车内置式永磁同步电机，建立控制模型、电磁模型和结构模型，分析恒转速调速和弱磁调速等工况下的振动噪声频谱特性。王晓远等[8]针对电动汽车永磁同步电机建立优化前后的电磁场模型、结构振动响应模型，分析了优化措施对电机电磁噪声特性的影响。Besnerais[9]对永磁同步电机空载工况的径向和切向电磁力进行仿真计算，发现电机磁极数和槽数的最小公倍数与径向电磁力的频率有关。王宇等[10]采用边界元法计算车用永磁同步电机的电磁噪声，分析了定子槽口宽度和磁体圆角半径等因素对电磁力和电磁噪声的影响。Lin等[11]对不同谐波条件下的永磁同步电机电磁力、电磁振动噪声进行仿真计算与影响因素分析。肖阳等[12]对正弦脉宽调制变频器的输出谐波及电磁力波进行推导，并开展电磁-结构-噪声仿真计算。Zhao等[13]结合有限元方法与多目标遗传算法，对高速永磁同步电机进行多物理场仿真分析，得到折衷的解决方案。相龙洋等[14]对电动汽车的永磁驱动电机进行台架试验，获得了电机的振动噪声特性。

本文以某地铁车辆用永磁同步电机为研究对象，分析电机产生电磁力波的理论，开展顺时针和逆时针转向加减速条件下的振动噪声测试，获得不同工况下的电机噪声特性，可为永磁同步电机的应用提供指导。

1 永磁同步电机电磁力波的理论

永磁同步电机由逆变器供电，不计铁心磁阻及饱和的影响时，考虑l次电流谐波的气隙磁通密度为

b(θ,t)=Bsl+Bpm=

Bsl,Λ0l+Bsl,Λkl+Bpm,Λ0+Bpm,Λk=

(1)

式中:Bsl,Λ0l和Bsl,Λkl分别为平均磁导调制和开槽磁导调制产生的定子磁场，Bsl为两者之和；Bpm,Λ0和Bpm,Λk分别为平均磁导调制和开槽磁导调制产生的转子磁场，Bpm为两者之和；Bν,Λ0l和Bν,Λkl分别为平均磁导调制和开槽磁导调制产生的定子磁场气隙磁通密度幅值；Bμ,Λ0和Bμ,Λk分别为平均磁导调制和开槽磁导调制产生的转子磁场气隙磁通密度幅值；ν和μ分别为定子和转子的谐波次数；p为永磁同步电机极对数；θ为转子机械角度；ω为基波磁势角频率；z为定子槽数；t为时间；φν为第ν次定子电枢谐波初相位。

根据麦克斯韦应力张量法，忽略切向磁通密度，单位面积径向电磁力波为

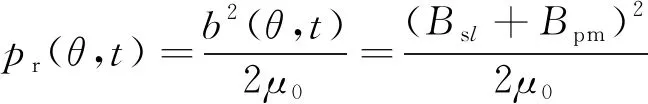
(2)

式中:μ0为真空磁导率。

定子磁场产生的径向力波可分为平均磁导调制定子磁场相互作用产生的电磁力波、平均磁导调制定子磁场和定子开槽磁导调制定子磁场相互作用产生的电磁力波、定子开槽磁导调制定子磁场相互作用产生的电磁力波3个部分，相应的径向力波阶数分别为(ν1±ν2)p、(ν1±ν2)p±kz和(ν1+ν2)p±2kz，其中，k为磁导谐波次数[7]。

定转子磁场相互作用产生的径向力波可分为平均磁导调制定转子磁场相互作用产生的电磁力波、平均磁导调制转子磁场和定子开槽磁导调制定子磁场相互作用产生的电磁力波、开槽调制转子磁场和平均磁导调制定子磁场相互作用、定子开槽磁导调制定转子磁场相互作用产生的电磁力波4个部分，相应的径向力波阶数分别为(μ±ν)p、μp±νp±kz、μp±νp±kz和μp±νp±2kz。

2 永磁同步电机的测试说明

某地铁车辆用风冷永磁同步电机的额定功率为190 kW、极对数为4、转速范围为0～3 200 r/min。为获得该电机的噪声特性，并分析噪声与振动的关系，利用B&K振动噪声测试系统在半消室中开展噪声与振动测试。

噪声测试采用五点法进行测量，噪声测点N1～N5分别位于永磁同步电机的传动端、左侧、后端、右侧和顶部中心线，距离电机包络面1 m处。振动测点V1～V3分别位于永磁同步电机的后端正上部、右侧中间位置和传动端正上部。三向加速度传感器的轴向、垂向和横向分别表示与电机轴平行、垂直于地面和平行于地面且垂直于电机轴。转轴上布置有转速传感器。测试现场如图1所示。

图1 振动噪声测点布置

永磁同步电机的测试分4种工况。测试工况1是顺时针转向，以每级间隔200 r/min逐级加速至3 200 r/min；测试工况2是逆时针转向，以每级间隔200 r/min逐级加速至3 200 r/min；测试工况3是顺时针转向，连续加速至3 200 r/min后断电；测试工况4是逆时针转向，连续加速至3 200 r/min后断电。

3 永磁同步电机的噪声特性分析

3.1 A计权声压级分析

由于永磁同步电机的电磁噪声具有离散频谱的特点，容易出现尖锐刺耳的声音，对人体感官造成不适，因此，分析频段取人耳听力频率范围20～20 000 Hz，对测试工况1和测试工况2各转速下的A计权声压级进行统计分析，得到如图2所示不同转速下的总噪声对比。可以看出：(1) 200～800 r/min的平均噪声近似从55.7 dB(A)线性增加到72.8 dB(A)，800～2 000 r/min的平均噪声在73 dB(A)附近变化不大，2 000～3 200 r/min的平均噪声变化趋势呈现波动，在2 400 r/min和3 200 r/min时存在噪声峰值，分别为79.1 dB(A)和81.4 dB(A)；(2) 600、800、2 200 r/min时，顺时针旋转的平均噪声较逆时针旋转高1.5～2.5 dB(A)，其余转速下转向的影响在1 dB(A)内；(3)测点N4和N5在800 r/min和2 400 r/min时存在峰值。

3.2 1/3倍频程分析

图3为顺时针转向200 r/min、1 900 r/min和3 200 r/min转速的A计权声压级1/3倍频程。可以看出：200 r/min时，4 000 Hz和500 Hz在全频段中的贡献最大，且测点N4在500 Hz的噪声明显高于其余测点；1 900 r/min时，1 600 Hz在全频段中的贡献最大；3 200 r/min时，400 Hz和2 500 Hz在全频段中的噪声较大，且测点N4和N5在400 Hz的噪声明显高于其余测点。

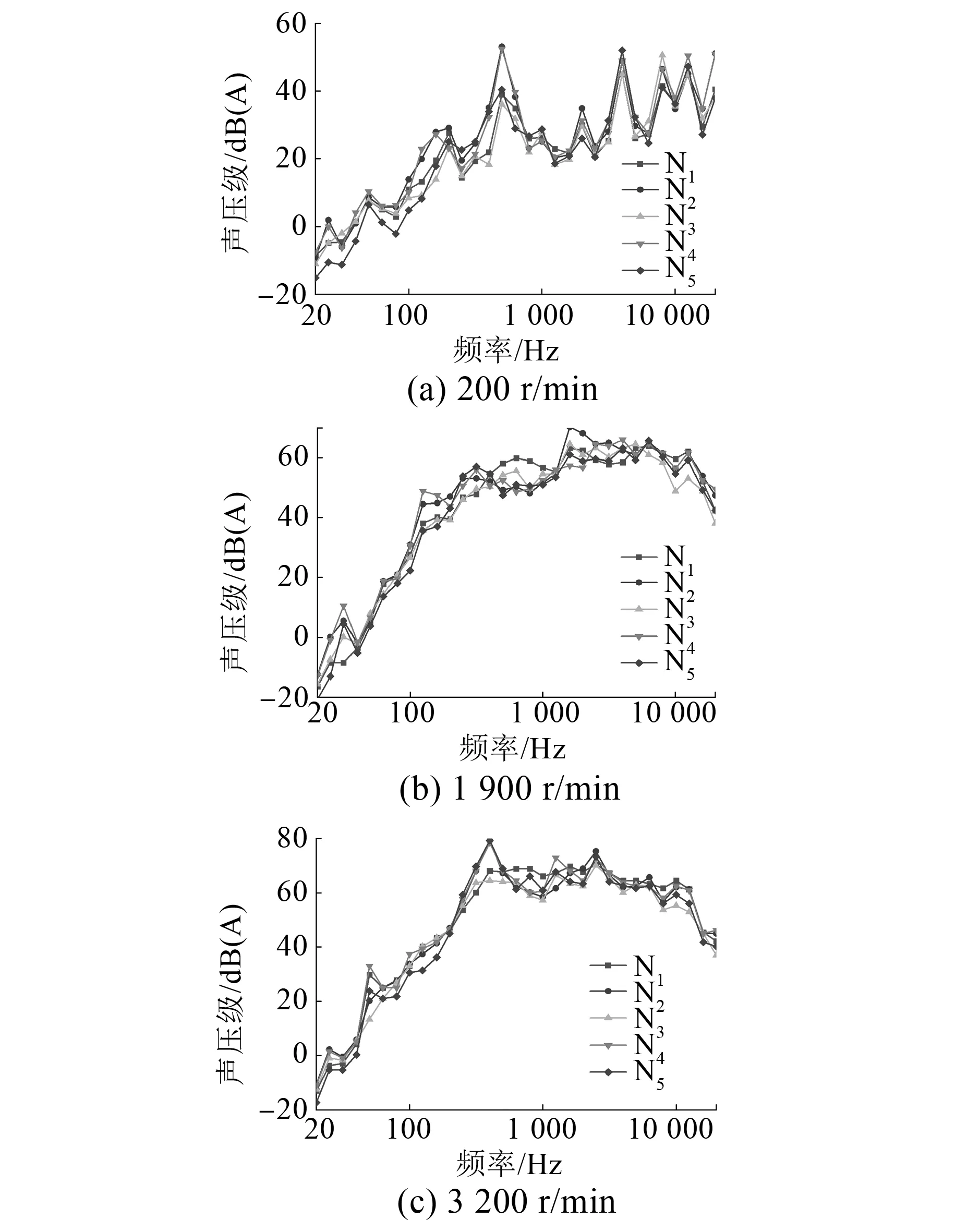
图3 不同转速的1/3倍频程分析

3.3 噪声随转速变化关系分析

3.3.1 噪声时域信号

图4为测试工况3的时域信号，可用于定性分析噪声随转速的变化过程。由图4可以看出永磁同步电机加速过程中的噪声变化大致有以下特点：(1) 470 r/min左右，噪声突然增加，可能存在共振现象；(2) 600～1 000 r/min，噪声在增加过程中存在波动；(3) 1 000～2 000 r/min，噪声近似维持稳定；(4) 2 000～3 000 r/min，噪声迅速增加后维持稳定，但在2 400 r/min附近形成峰值；(5) 3 000～3 200 r/min，噪声迅速增加后维持稳定。

图4 测试工况3的噪声时域信号

3.3.2 总噪声随转速变化

为定量分析噪声随转速的变化关系，图5给出测试工况1各测点噪声随转速变化的曲线，其余工况的结果未列出。可以看出：(1)在470 r/min，测点N1、N2、N4和N5的噪声存在峰值，N3的噪声峰值较小；(2) 600～1 000 r/min，噪声值在增加过程中存在较大波动，噪声峰值所在转速为710、790、830、940 r/min等；(3) 1 000～2 000 r/min，噪声值维持稳定，波动较小；(4) 2 000～3 200 r/min，噪声逐渐增加，在2 010 r/min和2 390 r/min附近个别测点噪声存在峰值。

图5 测试工况1的各测点噪声随转速变化曲线

图6为加速和减速时测点N1的噪声曲线对比。可以看出：减速过程没有开关频率的作用，在3 200～1 000 r/min减速过程中的噪声值下降较快，但在1 000 r/min以下，减速过程和加速过程变化趋势接近，说明开关频率作用主要体现在1 000 r/min以上。

图6 加速和减速时测点N1的噪声曲线对比

3.3.3 频谱随转速变化

图7为测点N5的转速-频率-声压级色谱图。由图7(a)所示的顺时针加速的转速-频率色谱图可知：永磁同步电机噪声主要由电磁激励造成，频谱表现为以(0 Hz，0 r/min)为原点固定斜率的阶次信号和开关频率(2 000 Hz)及倍频(4 000、6 000、8 000 Hz等)为中心固定斜率的调制信号组成，对噪声影响较大的阶次信号包括56阶、48阶、104阶和8阶等。从前述永磁同步电机电磁力波理论可知，由于定子、转子的谐波次数ν和μ均为奇数，整数槽电机的槽数z是极对数p的整数倍，电磁力波的空间谐波阶次可表示为极对数的偶数倍，测试所得的阶次与理论分析一致。IGBT器件开通关断时，由于正弦脉宽调制的作用，高频的电磁力频率主要分布在开关频率两侧，与开关频率相差奇数倍的电流基频，该特征在图7(a)中表现明显。由图7(b)所示的顺时针断电减速的转速-频率色谱图可知：频谱仅存在与转速强相关、以(0 Hz，0r/min)为中心的阶次激励作用，无开关频率及调制信号激励。

图7 测点N5的转速-频率-声压级色谱图

图8为顺时针加速时测点N5的阶次贡献分析结果，其他测点的结果未列出。由图8可知：(1) 1 000 r/min以下，贡献最大的阶次为56阶和104阶，其中56阶激励在470r/min时很可能引起共振导致噪声突然增加；(2) 1 000 r/min以上，阶次激励和以开关频率为中心的调制信号共同决定噪声大小，尤其是当阶次激励与调制信号或开关频率及2倍开关频率附近的调制信号相交时，噪声叠加，导致该转速的噪声增加；(3)转速增加至3 200 r/min时，8阶激励可能引起结构共振。断电过程的阶次激励与加速过程相同，主要表现为48阶、56阶和104阶等阶次激励作用，无开关频率作用。

图8 测点N5的阶次分析

图9为470 r/min和3 200 r/min等典型转速下测点N5的噪声频谱。进一步证明了噪声主要由56阶、48阶、104阶及开关频率(2 000 Hz)附近的调制信号决定。当阶次激励频率与结构固有频率接近时(如470 r/min时，在440 Hz对应56阶处)，噪声出现峰值。当阶次激励与调制信号频率相交时噪声出现叠加，如2 390 r/min，在2 478 Hz附近。

图9 典型转速下测点N5的噪声频谱

4 永磁同步电机噪声与振动的关系

图10为典型转速下永磁同步电机振动有效值对比，分析频段为0～25.6 kHz。可以看出：位于电机后端盖上部测点V1的振动以垂向为主，最高量级在15 m/s2左右，且振动随转速变化不明显；位于电机右侧中间位置测点V2的振动以横向为主，在低转速时(如200、600 r/min)振动较高，最高为32.6 m/s2，在1 000 r/min转速以上振动较为平稳；位于电机前端盖上部测点V3的振动以垂向为主，在1 800 r/min以下振动变化不大，但在1 800 r/min以上振动较大，最高达到37.5 m/s2。

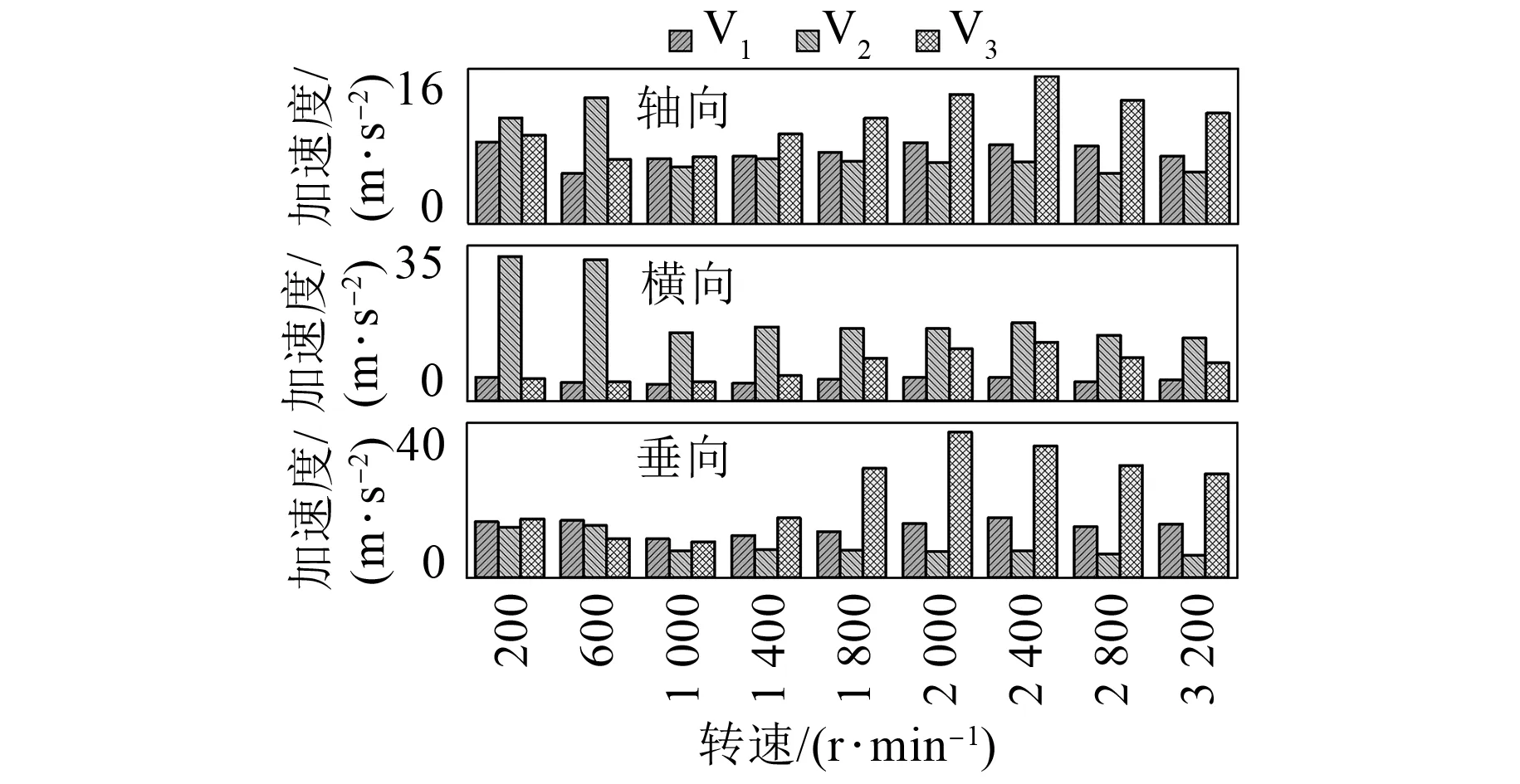
图10 典型转速的振动有效值

图11为振动测点V1～V3振动有效值随转速变化曲线。可以看出：1 000 r/min以下，在260、700、910 r/min等转速的振动存在较大波动，测点V2的垂向表现出非常明显的特征，这与电机定子结构的模态振型有关；1 000～2 000 r/min，振动较为平稳；2 000 r/min以上，测点V3的垂向振动增加明显。

图11 各测点振动有效值随转速变化曲线

为阐述永磁同步电机噪声与振动的对应关系，图12列出加减速过程中测点V3的转速-频率-垂向振动色谱图，其他振动测点及方向的结果未列出。振动色谱图和前述噪声色谱图一致，加速过程主要由48阶、56阶和104阶等阶次激励以及开关频率附近的调制信号组成，在316、440、910 Hz附近可能存在共振现象，而减速过程主要由48阶、56阶和104阶等阶次组成，无开关频率信号。

图12 测点V3的转速-频率-垂向振动色谱图

当永磁同步电机气隙径向电磁力波的频率接近电机固有频率时，会引起共振，从而产生较大的振动噪声。为此，对永磁同步电机的定子结构及机壳进行模态仿真。定子结构由各向异性的硅钢片叠压组成，为模拟硅钢片的叠压效果，将叠片平面方向视为各向同性，垂直于硅钢片方向的弹性模量小于硅钢片材料[15]。图13为定子结构及机壳处于自由状态下的部分模态振型。在未对电机的安装孔施加约束的情况下，得到的前6阶为刚体模态，频率接近0 Hz。第7阶的模态振型出现在绑扎线缆的连杆上，第8阶的频率461 Hz与测试的440 Hz共振点频率较接近。模态仿真的频率与振动噪声测试中的共振点频率存在差异的原因主要是测试的电机为整体结构，端盖和转子会对定子及机壳产生影响。从电机的模态振型可以看出径向模态是导致电机振动噪声的主要原因。

图13 定子结构及机壳的部分模态振型

由于永磁同步电机结构非常复杂，且变流器的输出电流谐波成分丰富，永磁同步电机的噪声振动和其拓扑结构、极槽配合、转子-永磁体设计等具有较强的关联。后续可进行实际输入电流波形下的电机电磁场仿真分析，基于电机的结构有限元模型进行电磁振动仿真分析，利用声学仿真软件进行电机的噪声仿真分析，并结合电机的振动噪声测试数据开展深入研究，从而更好地指导电机产品的设计与应用。

5 结 语

通过对某地铁永磁同步电机开展振动噪声测试及特性分析，得到以下结论：

(1) 200～800 r/min的平均噪声近似从55.7 dB(A)线性增加至72.8 dB(A)，800～2 000 r/min的平均噪声在73 dB(A)附近，2 000～3 200 r/min的平均噪声变化趋势呈现波动，2 400 r/min和3 200 r/min处存在的峰值噪声分别为79.1 dB(A)和81.4 dB(A)。

(2) 电机噪声主要由电磁振动产生，加速过程的主要频谱成分包括48阶、56阶和104阶等阶次成分和以开关频率(2 000 Hz)及其倍频为中心的调制成分，减速过程无开关频率作用，其余阶次成分一致。

(3) 电机在316、440、910 Hz等频率处存在局部模态，在电机阶次激励作用下易引发共振，导致噪声在起动过程中存在较大波动。