基于DBSCAN与LOF算法的共享汽车计价和停车点策略分析

李小龙，马英奇

（1.安徽理工大学 电气与信息工程学院，安徽 淮南 232001；2.安徽理工大学 计算机科学与工程学院，安徽 淮南 232001）

0 引言

共享汽车是基于互联网共享经济、车联网基础下的一种新兴交通出行服务方式，把更多用户在出行方面的需求集中为一种汽车共享出行模式。由于共享汽车的使用较为简单，在手机APP上就能完成注册、认证、订车和还车的全部过程，还支持芝麻新型等免押金服务，减少了因交换押金产生的服务纠纷，这种就近取车、灵活换车的方式吸引了大批用户。但是，这种用车方式给企业增添了很多麻烦[1-2]。在车辆安置问题上，会产生某些地区急需用车而订不到车的问题，为此企业采用“分时租赁”模式来解决这个问题，但仍存在着企业收益较低，成本花费较大的问题。

1 整体思路

对于定价方案，主要是制定合理的价格，来提高企业的利润。但要注意价格较低可能会造成更多的共享汽车使用量，同时造成更大的共享车调度时间，更长的员工工作时间和更高的调度成本，调度不合理会更加降低利润。价格较高可能会造成城市外围的使用者不再使用共享汽车，转而去使用地铁、公交车等其它交通工具，因此，合理的定价更能吸引使用者。首先对附件数据清洗，并找到该城市的人口密度和消费能力与其交通状况的相关信息，对信息与数据进行预处理，然后建立共享汽车的概率模型，并在以企业最大利润作为目标函数的基础上建立多元目标优化模型。由于交通状况，消费能力，人口密度等不同因素的影响因子不确定，本文在原有模型的基础上，提出基于DBSCAN算法的模型改进，得到打包改进后的共享汽车分布示意图并结合前述的多元目标函数，得出部分打包定价结果。

由于共享汽车的停车点是公司租用的，考虑到租赁费用高昂并结合第一阶段的数据分布特点，研究是否可以减少停车点的数量，其中共享汽车分布密度对汽车停车点的数量产生影响。先统计一个附件中的各个时区共享汽车停车点的数量，发现在不同的时间段及位置，因为人流量有所不同，这给改变共享汽车停车点的数量带来了可能性。一般情况下，共享汽车与用户之间距离较近时能够吸引用户选择，这是由于可以节省用户的时间和经济成本。本文采用LOF离群因子对共享汽车的分布密度进行刻画，对象的局部离群因子，每个共享汽车车辆编号P都被分配一个局部离群因子。

2 共享汽车的概率模型

该概率模型是建立起共享汽车的概率与其他因素的函数关系，在此概率模型的基础上参考以色列的特拉维夫市的人口、交通状况、消费能力等相关情况，建立数学模型，给出使得企业利润最大的共享汽车按小时计价方案。完成共享汽车按小时计价方案因素具体有以下几个原因：共享汽车离用户的距离、共享汽车间的离散度、共享汽车到达目的地的难易程度、到达目的地交通便利程度、人口以及消费能力。

3 多目标优化模型的建立

3.1 自变量考虑范围

在考虑自变量范围时，需要明确自变量的数量及与因变量的关系，由此可得到逻辑框图如下图1所示。

图1 共享汽车定价逻辑框图

3.2 约束条件

为了使目标达到最优，对位优化之前的定价总额M与平均成功率N，有如下约束条件：

在执行共享汽车的定价与未被执行的定价之间有一个的区域，本文称之为合理定价范围，即被执行的共享汽车定价略微降低或未被执行的共享汽车定价略微提高，在这个范围内都有可能被执行。设PF为失败共享汽车的定价，PS为成功共享汽车的定价，合理定价应该满足：

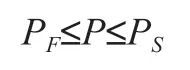
执行率优化是定价总额一定的情况下执行概率，定价优化是执行率一定情况下的优化执行率，为了使得目标函数量最优化，本文给出的优化模型如下：

其中，Si为 优化后的第i个共享汽车的成功率，Pi为 优化后第i个共享汽车的定价，PFi为第i个共享汽车对应的失败共享汽车定价，PSi为第i个共享汽车对应的成功共享汽车定价。

3.3 最优函数最优解求解

本文引入最大期望利润W，设每一个共享汽车商家提供给系统的价格为Q，系统定价为Qi′，该共享汽车执行率为Ri，则最大系统期望利润可以近似用如下公式估计：

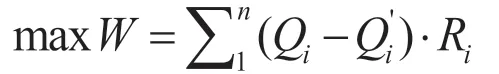
也即能求出期望利润最大时的定价总额与平均成功率的值。

该模型包含了上文的最优定价选择以及如何打包与打包共享汽车定价的最优方案，并且对打包方案进行检测，在实际应用中具有较好的实用性。

4 基于DBSCDN算法的模型改进

改进模型之前，本文需要明确打包的目的，事实上打包的目的与本文上文考虑的两个因素—执行率与定价密切相关。

打包对执行率的影响：在打包过程中，并不是随机打包距离近的点，而是尽量将预计不能成功执行（执行率低的点）和能成功执行（执行率高的点）进行打包，这样能大大提高执行率低的点的执行率[3]。

打包对定价的影响：打包的任务点定价总和应该小于三个任务点分别定价的总和。事实上打包成功率较高的任务点对于系统盈利来说是不利的，打包对系统盈利的好处是提高平均成功率从而提高期望利润[4]。

尽量联合成功执行率高的与低的共享汽车点并打包，同时，考虑到实际共享汽车执行用户不可能一次性乘坐多辆共享汽车，本文规定打包共享汽车数量上限不超过4个。对于打包完的集合，需要根据其周围的用户分布以及用户情况来判断打包是否合理，并将不合理的包打散[5-6]。

本文将某个区域的三个预打包共享汽车T1、T2、T3，两个用户a1、a2，此时他们的用户得分半径不能覆盖任何一个共享汽车，即不合理打包。加入用户a3，其用户得分半径覆盖到原T3，即合理打包。

在寻找打包共享汽车最近的用户，先确定多共享汽车中心点，其GPS坐标由共享汽车的平均经度与平均纬度确定。寻找该中心点最近的用户距离，将该用户到这若干个共享汽车的折线距离转换成直线，示意图如下图2所示。a1为距离相应共享汽车最近的用户，且其用户得分半径覆盖共享汽车。本文将该用户的轨迹T1→T2→T3→T4距离a1至的直线距离其中T4'的直线距离：

图2 共享汽车等效距离示意图

在共享汽车的定价方案确定之前，本文先猜测定价p由两部分组成，即共享汽车本身价值p1与路途费用p2。而对于打包共享汽车来说，共享汽车本身价值p1没有发生变化，变化的为路途费用p2，设a1与T1、T2、T3、T4共享汽车的直线距离分别为d1、d2、d3、d4，打包后a1到四个共享汽车的等效距离为a1至T4'的直线距离D。此时，路途费用P2'的算方式如下（假设路途费用与路途距离成正比）：

设共享汽车i本身价值x、路途费用y与定价Pi服从的函数关系如下：

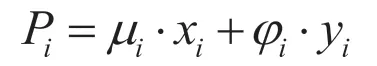
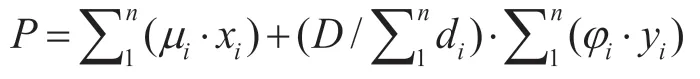
其中D为等效距离，di为用户到原i个共享汽车的距离。

将数据导入到MATLAB中记为X，通过程序检验聚类结果个数，调整聚类结果到合适区间，下图3为DBSCAN模型求解的图示结果。

图3 DBSCAN模型求解的图示结果

本文根据原数据对定价方式进行拟合判断，得到每个打包任务较为合理的定价。本文列出部分任务的定价如下表1所示：

表1 部分打包定价结果展示

5 LOF算法的建立

LOF算法通常是用来判断局部异常的离群点，本文尝将离群因子作为停车点的数量的规律估计的一个因素。离群因子的算法流程如下：

（1）计算共享汽车车辆编号p的k距离。共享汽车p的k距离dk(p)为p到某个临近的共享汽车q之间的距离，q是离P最近的第k个共享汽车。

（2）计算p的k距离邻域Nk(p)，Nk即离点p最近的k个共享汽车组成的集合。

（3）计算p相对于共享汽车q的可达距离dk(p,q)，给定自然数k，p相对于q的可达距离为p到q点的距离dk(p,q)，d与dq中的较大值：

（4）计算p的局部可达密度P(p)，p的局部可达密度等于共享汽车点p的平均可达距离的倒数：

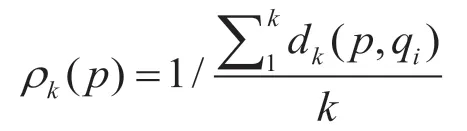
（5）计算共享汽车点p的局部离群因子O：

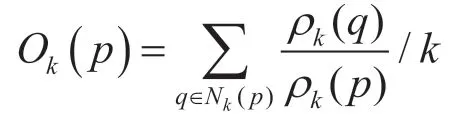
离群因子数值越大，该共享汽车点的周围共享汽车分布密度越小，该点越离群；反之，离群因子数值越小，该共享汽车点分布密度越大，该点离群程度越小。离群因子针对共享汽车与共享汽车及用户之间的分布关系。由于离群因子直接判断共享汽车局部密度，比直接判断共享汽车与共享汽车之间的距离更加能体现共享汽车分布的情况。将离群因子通过变换转换为每个点的定价得分因子，可进行下一步定价规律的研究。

6 模型结果分析

通过LOF算法并结合第一阶段的数据分布特点可知，在LOF值大即离群程度越大的地方，可以适当减少停车位的数量，在LOF值小即离群程度越小的地方，由于交通便捷，人口密度较大，共享汽车停车位的数量不宜减少。据此本文做出改进后的部分离散共享汽车停车位的分布示意如下图4所示。

图4 改进后的部分离散共享汽车停车位的分布图

7 结语

本文考虑到的共享汽车计价方案优化影响因素较多，建立的机理模型适应性较强，回归效果良好。使用一系列创新算法，实际表现良好，如研究共享汽车停车点时采用了LOF离群因子进行分析；在研究共享汽车计价时，对DBSCAN算法进行改进，接着对打包后的包进行可行性分析，与原方案对比后发现表现良好。采用的LOF离群度检验的算法对推广用于电子商务犯罪检测、网络入侵检测、生态系统失调检测和公共卫生医疗等领域中，具有一定的启发作用。