间谐波对基波测量误差的影响分析
2021-10-23亓富军田质广彭静牛庆松
亓富军,田质广,彭静,牛庆松
(1.国网临沂供电公司,山东临沂,276000;2.临沂大学信息学院,山东临沂,276000)
0 引言
近年来,由于电力电子装置在电力系统中的大量应用,特别是晶闸管变频调速电路和电弧炉等波动性负荷的增加,电力系统中除了谐波以外还存在大量的间谐波(interharmonic)。目前,国际上已经对有关间谐波的电能质量问题展开广泛的研究,分析间谐波的产生、危害、测量和消除方法[1-3]。而国内对于间谐波的研究很少,间谐波对于基波测量误差的影响[4],在国内外文献中未见深入分析研究。
本文借助计算仿真工具MATLAB 对间谐波引起的基波测量误差进行了分析,主要分析不同频率和幅值的间谐波对电压和电流测量值的影响,提出当存在间谐波时提高基波测量精度的措施。
1 间谐波和交流采样算法简介
1.1 间谐波简介
间谐波为非整数倍基波频率的电压和电流信号。它们可以呈现为离散频率或宽带频谱。IEC 61000-2-2 将间谐波定义为:任何非整数倍基波频率的频率。IEEE 的间谐波工作组也采用了这个定义,并将其引入IEEE 519 标准。
电力系统中许多设备都能够产生间谐波,如变频调速装置、电弧炉等。另外,许多波动性的负载也会在电力系统中引起间谐波。间谐波和传统的谐波类似,能够产生许多危害。另外,频率低于基波的间谐波(又称次谐波,subharmonic)还能够引起电压闪变和低频继电器的异常动作。
因此,有必要对电力系统的间谐波含量进行测量,并研究降低间谐波危害的措施。当系统中存在较大间谐波时,目前一般建议采用谐波滤波器来治理。但是由于实际系统中的间谐波频率往往是不断变化的(例如变频驱动系统),而且也难以精确快速地测量间谐波,因此要实现间谐波的治理还存在许多困难。
1.2 交流采样算法简介
交流采样算法应该能准确地反映电压、电流的有效值及平均功率值等。电力自动化监控和保护装置中,常用的一种交流采样算法如下:
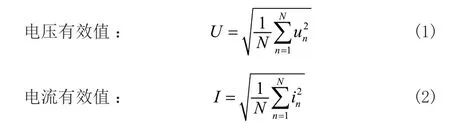
其中:N 为采样点数;un 和 in 分别为电压、电流采样值。
采样频率应当为实际系统频率的整数倍,各采样点之间应该是等时间间隔,即整分割采样。对于常用的单周期采样,N 实际就是每周期的采样点数,一般采样32、64 或128 点。目前一般要求测量装置对电压和电流的测量精度不低于0.5级,较先进的产品则可以达0.2 级。由于这是计及PT/CT 误差和A/D 变换器误差等多种因素后的总误差,因此交流采样算法本身带来的理论误差应当更小,才能保证测量设备的精度指标。
2 间谐波对基波测量误差的影响
交流采样算法中常要计算的基波电压和电流有效值,本文主要分析间谐波对基波测量误差影响。为了准确地评价不同频率和幅值的间谐波对测量误差的影响,本文设定分析信号只包含基波和一个间谐波:
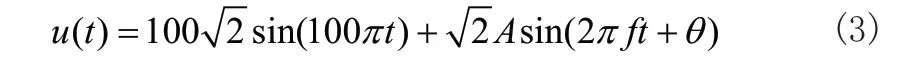
其中基波频率为50Hz,有效值为100。间谐波的频率为f,有效值为A,初相角为θ。仿真分析中间谐波的频率分别取25Hz、60Hz 和180Hz,代表次谐波、低频和高频间谐波,更高频率的间谐波一般幅值很小,本文不再讨论;有效值分别取基波有效值的10%、1%和0.2%;间谐波的初相角则允许从0到360 度任意变化。由公式(1)和(2)可以看出,电压和电流的交流采样算法实际是相同的,因此采用公式(3)对于电压间谐波的分析结果同样适用于电流间谐波。
为便于分析,本文借助MATLAB 中simulink 工具,搭建仿真模型分析(见图1)。图中U1、Uf 分别代表基波、间谐波。
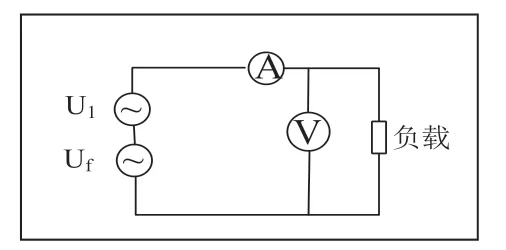
图1 分析模型
2.1 单周期交流采样,间谐波对基波电压测量误差影响
2.1.1 当周期测量错误时存在的电压测量误差
交流采样装置中,一般采取测频电路来实时跟踪系统频率和周期的变化。当采用过零点检测方法来测量周期时,容易受到间谐波的干扰而测得错误的周期值。利用这个错误的周期值去确定采样间隔,就容易给基波电压有效值的测量造成误差。每周波采样点数N=32 时,此时间谐波对基波电压测量造成的最大误差如表1 所示,其中使用的是百分比相对误差。
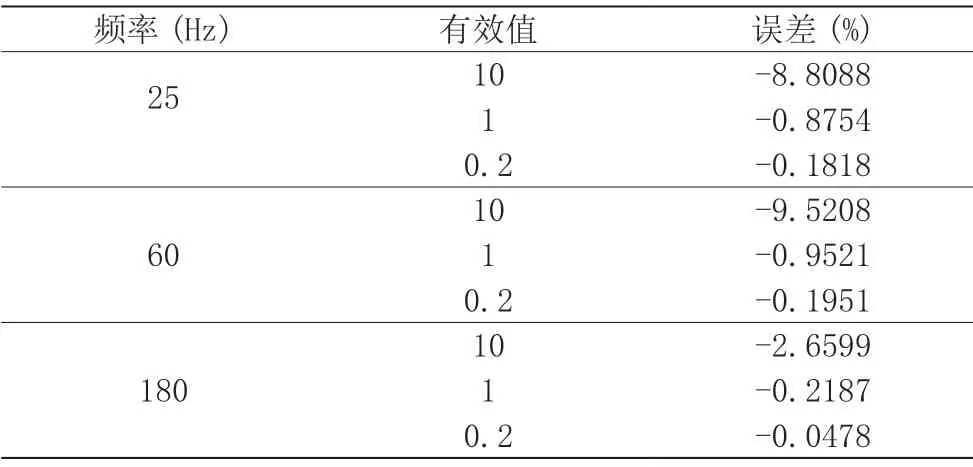
表1 周期测量错误时的电压测量误差
由表1 可见:
(1)间谐波会给基波电压有效值的测量造成误差。而且间谐波的含量越大,造成的测量误差也越大。
(2)电压测量误差与间谐波幅值近似呈线性关系。
继续增大采样点N,分别取64、128、1024,得到的误差见表2。

表2 增加每周波采样点数N 时的电压测量误差
(1)增加每周波采样点数N 时,测量误差时大时小。这是由于误差与绝对采样剩余时间有关,增加采样点数可能使绝对采样剩余时间超出50%采样间隔,反而增大误差,这与文献[4]的分析结果是相似的。
(2)测量误差的变化非常小,不足0.01%,基本可以忽略不计。因此,可以说当N ≥32 以后,继续增加每周波采样点数对于减小测量误差基本无影响。
比较表1 和表2 可见:
2.1.2 当周期测量正确时存在的电压测量误差
为了满足交流采样装置跟踪系统频率和周期的需要,已经有许多文献提出了能够比较准确地测量频率的算法。假设采用这些算法后,交流采样装置已经能够准确测量出系统的实际频率和周期。下面来分析此时间谐波对基波电压有效值造成的最大测量误差,采样点数N=32,分析结果见表3。
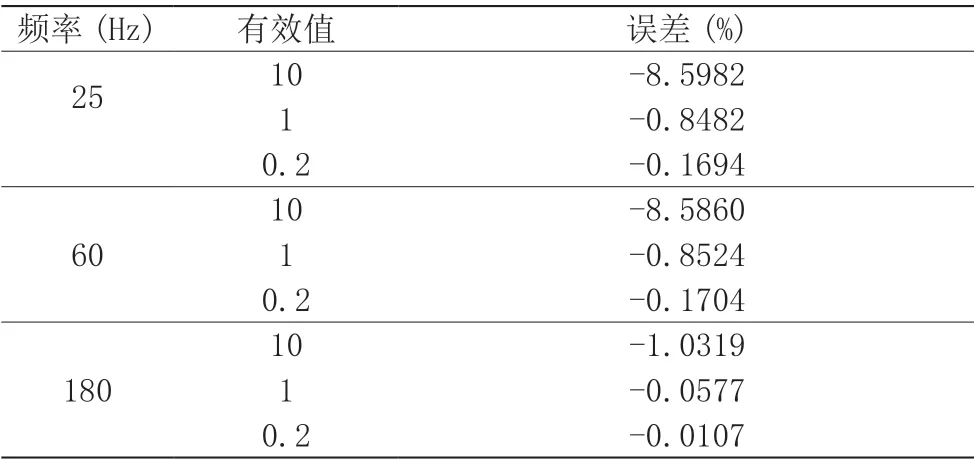
表3 周期测量正确时的电压测量误差
比较表1 和表3 可见:
(1)准确跟踪系统频率能够减小测量误差,但是不太显著。
(2)本文在增加每周波采样点数N 后进行了实验,但是实验结果与表3 基本相同,表明增加N 对于减小电压测量误差基本没有效果。
(3)表3 显示当存在含量为0.2%的60Hz 间谐波时,测量误差约-0.17%。进一步的分析证明含量为0.2%的40Hz 间谐波会造成-0.21%的测量误差。可见即使间谐波的含量只有0.2%,也会使交流采样装置不可能达到0.2 级的精度,要达到0.5 级也更困难。
上述的最大测量误差是在确定间谐波的频率和幅值后,令间谐波初相角在0 到360 度变化时计算出来的。下面对幅值为1 的间谐波,分析不同的初相角对基波电压测量误差的影响,如图2 所示。
由图2 可见,当间谐波初相角不同时,基波电压的测量误差不同,即误差与测量的起始时刻有关。在实际应用中,要在对应间谐波某个相角的时刻开始测量是难以做到的,因此测量误差不是常数而难以进行补偿,不利于测量精度的提高。
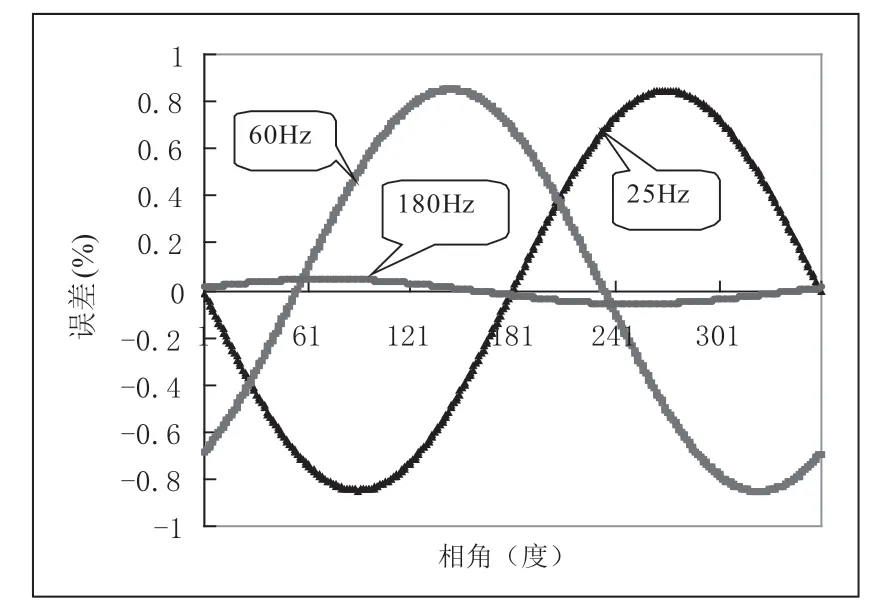
图2 间谐波初相角对测量误差的影响
2.2 多周期交流采样,间谐波对基波电压测量误差影响
单周期交流采样虽具有速度快等优点,但是它只能考虑到谐波的影响,而不能消除间谐波的影响。下面分析多周期采样方法。针对本文分析所用的间谐波频率,选采样窗口为10 个工频周期(即200ms)进行分析。
2.2.1 当周期测量错误时存在的电压测量误差
在系统中存在间谐波,且交流采样装置采用过零点检测等方法导致周期测量错误的情况下,通过将采样窗口增大到200ms,得到的基波电压有效值的测量误差见表4。

表4 采样窗口为10 个周期时的电压测量误差
比较表1 和表4 可见,增大采样窗口后,电压测量误差明显减小。比较表2 和表4 可见,增大采样窗口比准确的频率跟踪更有利于减小测量误差。
实际系统中电力设备和波动负荷产生的间谐波频率可能是随时变化的,且可能同时含有多种频率的间谐波。虽然理论上可以将采样窗口增大到1 秒,这样能够包含任意整数频率间谐波,但是这会显著增加计算量并降低测量速度。采样窗口取5 个工频周期(100ms)时的电压测量误差进行,分析结果见表5。
比较表4 和表5 可见,采样窗口偏小时电压测量误差会增大。比较表3 和表5 可见,即使采样窗口不是足够大,但是多周期采样比带有频率跟踪的单周期采样更有利于减小测量误差。
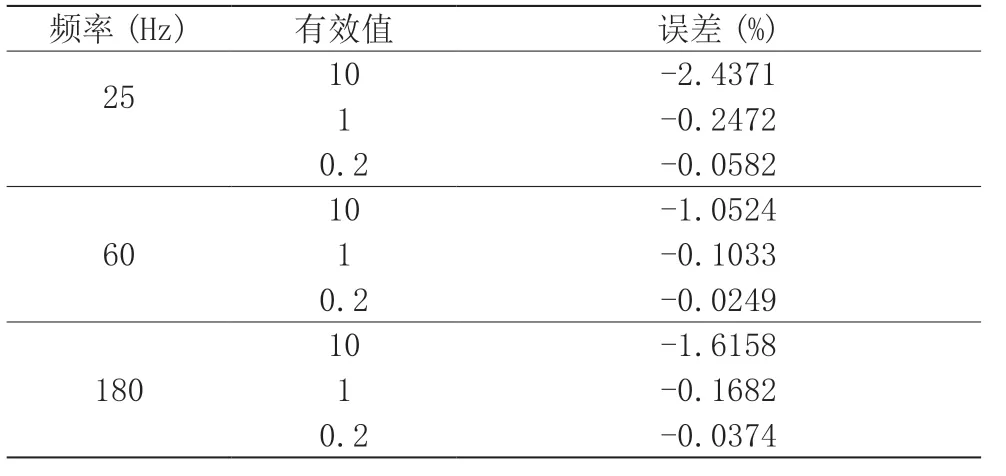
表5 采样窗口为5 个周期时的电压测量误差
本文在增加每周波采样点数N 后进行了分析验证,但是实验结果表明在多周期采样中增加N 对于减小电压测量误差基本无影响。
2.2.2 当周期测量正确时存在的电压测量误差
在系统中存在间谐波但是周期测量正确的情况下,分别取采样窗口为10 个周期(200ms)和5 个周期(100ms)时得到的基波电压有效值测量误差见表6。
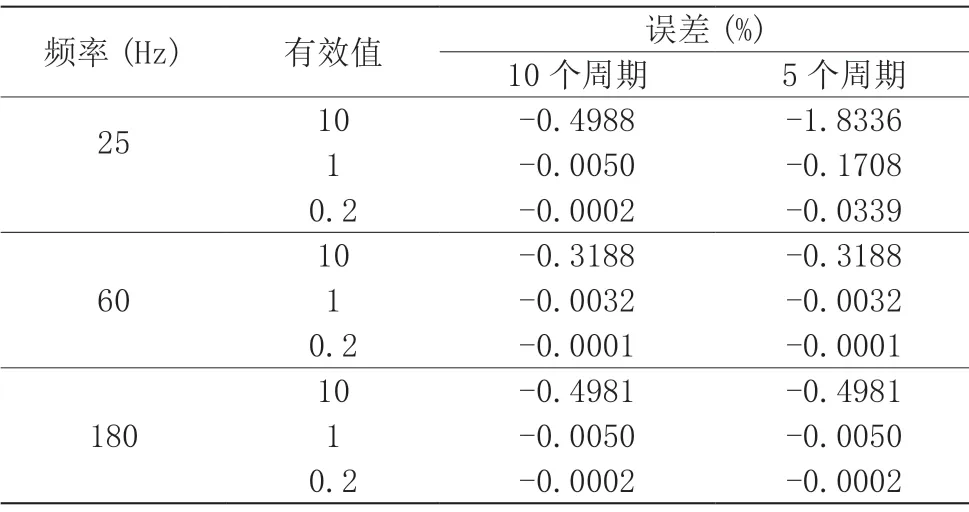
表6 周期测量正确时的电压测量误差
比较表4 和表6 可见,准确地跟踪频率后,电压测量误差明显减小。
表6 显示对于60Hz 和180Hz 的间谐波,采用5 个周期和10 个周期采样窗口时的测量误差完全相同。这是符合交流采样理论的。因为在50Hz 系统中,对60Hz 和180Hz 间谐波只需要达到10Hz 分辨率,即采用100ms 的采样窗口。而对于25Hz的间谐波,则至少需要5Hz 分辨率,即200ms 的采样窗口。
比较表5 和表6 可见,虽然理论上对60Hz 和180Hz 间谐波只需要5 个周期采样窗口,但是当频率测量错误(如表5)时采用5 个周期的采样窗口时就会造成较大的测量误差。
本文在增加每周波采样点数N 后进行了实验,但是实验结果表明增加N 对于减小电压测量误差基本没有效果。
下面分析当采样窗口为200ms,间谐波幅值为1 时,不同间谐波初相角对基波电压测量误差的影响,如图3 所示。
由图3 可见,采用多周期采样时,对某些频率(如60Hz和180Hz)的间谐波,其初相角对基波电压的测量误差没有影响。这样误差是常数就便于进行补偿,以提高测量精度。
3 结论
本文针对目前电力系统测量中普遍采用的交流采样技术,分析了存在间谐波干扰时的测量误差,得到以下结论:
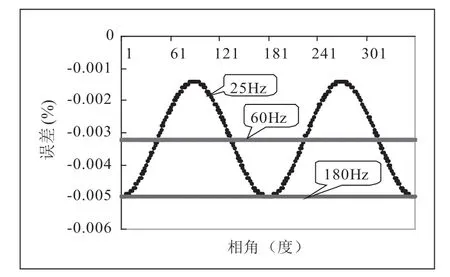
图3 间谐波初相角对测量误差的影响
(1)间谐波的存在对于交流采样测量误差有很大影响。分析表明即使按照IEC 标准保证系统间谐波含量不超过0.2%,也会使交流采样装置不可能达到0.2 级的测量精度。
(2)对常规的单周期采样,当每周波采样达32 点以后,继续增加采样点数只会增加硬件和软件负担,而对于减小测量误差基本没有效果。采用精确的频率跟踪算法有利于减小测量误差,但是效果不显著。
(3)存在间谐波时,减小交流采样测量误差,最有效的措施是改用多周期采样。多周期采样会影响数据采集实效性,电压扰动偏大时可借助多周期采样进行间谐波定量分析。
