具有长程相互作用振子环的同步动力学分析
2021-10-23唐智权朱留华
唐智权,朱留华
(1.梧州学院电子信息工程系,广西梧州,543002;2.玉林师范学院物理与电信工程学院,广西玉林,537000)
0 引言
复杂网络作为一种研究复杂系统行之有效的方法,在非线性动力学、生物学、统计力学、现代医学及工程技术等领域得到了广泛的应用[1-3]。这些应用主要包含两方面内容。一方面,一个高度交互的复杂系统可以通过一个图来恰当的建模,图中的节点表示动力学单元,连边表示它们之间的相互作用。从网络的角度来探究系统的全局特性相对比较容易,例如电网的稳定性、通信系统中数据包的传播特性;另一方面,研究相应的网络可为实际系统的操作提供预演,并有助于更好的控制、预测、优化或重构它们。
最近,复杂网络上的同步引起了科学家们的极大兴趣,因为它有助于人们更深刻地理解真实复杂系统的动力学过程的功能和结构[4-5],例如电力网络的级联失效、神经系统中神经元的异常同步。随着生物网络和社会网络的兴起,人们对复杂网络上非线性耦合振子的同步相变进行深入的研究[6-11]。Kuramoto 模型是研究非线性耦合振子同步的经典范例,振子间的同步与否取决于相位差的正弦值与振子固有频率之间的竞争[12]。
近年来,Kuramoto 模型得到了改进与延伸。一方面,为了获得理论解析结果,需采用全局耦合;另一方面,为了提高计算效率,需考虑有限范围或最近邻耦合。如何调节这一矛盾?在本文中,我们提出了一个按r α-规律衰减的长程耦合策略,其中α≥0 定义了其作用范围。若α=0 对应于全局均一耦合;α→0 对应于最近邻耦合。本文的主要目的在于揭示临界耦合强度对幂律指数α的依赖关系。
1 Kuramoto 模型的变体
本文考虑一个耦合振子环,单个振子的动力学演化满足下列方程:

式中N是振子总数,θi和ωi分别是第i个振子的瞬时相位和固有频率,k≥ 0表示系统的耦合强度,固有频率ωi服从N(0,1)分布,调节幂律指数α可以实现最近邻耦合和平均场耦合之间的切换。因为周期边界条件被采纳,所以两个振子之间的距离可表示:
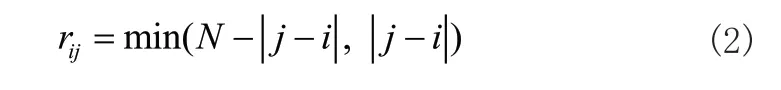
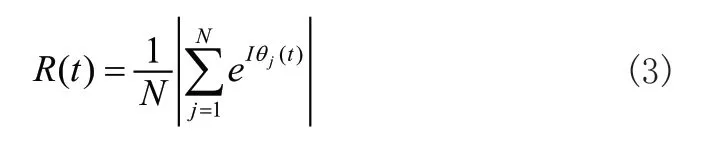
式中为I虚数单位;R(t) ∈ [0,1],表征系统中振子的相干程度,R(t)的值越大表示想干性越高。R(t)=1意味着系统中振子实现了完全同步。
对于全局均一耦合的情况α=0,耦合强度的临界值[12]:

式中ω0是固有频率分布的平均值。接下来我们讨论α≠ 0时耦合强度的临界值。
2 数值模拟与理论分析
图1 模拟了给定衰减指数α,不同系统尺寸下序参量随耦合强度增加的变化规律。图1 显示:系统的同步特性对系统尺寸不敏感,不同系统尺寸的曲线重叠在一起。对比图1(a)和(b)发现:临界耦合强度随α的增加而增大。
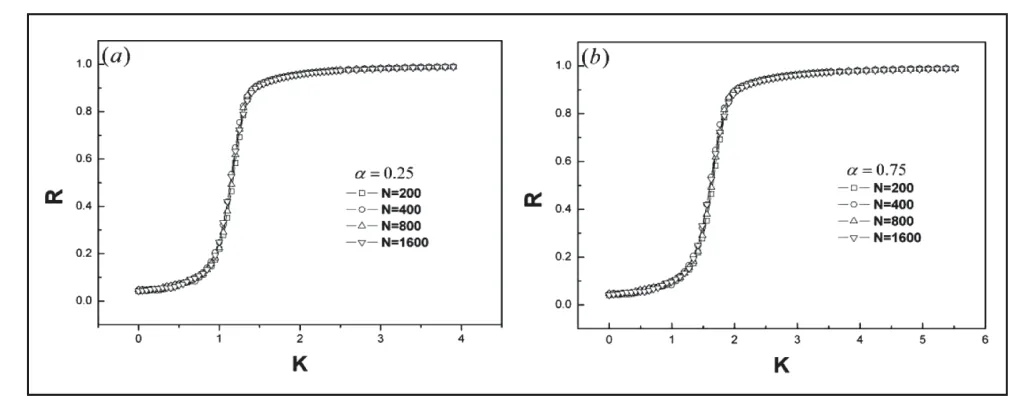
图1 不同尺寸的系统序参数R 随耦合强度K 的变化规律。(a)α=0.25,(b)α=0.75
耦合强度未被采用标度变换;(b)耦合强度已被采用标度变换。
图2 模拟了相同系统尺寸,不同衰减指数α下的序参量随耦合强度增加的变化规律。图2(a)显示:系统的同步特性对衰减指数α有很强的依赖性。图2(b)显示横坐标的适当缩放,使得4 条同步曲线几乎完全重叠,其中包括平均场曲线。依据这种尺度变换可以很容易地获得α≠ 0时耦合强度的临界值:
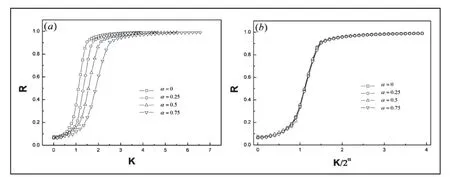
图2 不同衰减指数下序参量随耦合强度的变化规律,其中系统尺寸N=1600
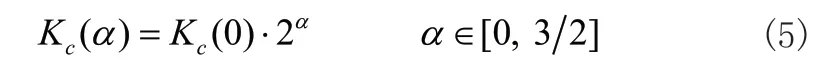
为什么要限定幂律指数的上限?先前的文献[13]已经证实:当振子数足够大且α> 32时,有限的耦合强度不足以使一维振子环取得全局同步。
如图3 所示,这种分析解与文献[14-15]的研究结果吻合的很好,从而有助于我们更好的理解幂律指数对振子环同步动力学行为的影响。

图3 由方程5 获得的幂律指数与临界耦合强度关系曲线
接下来,我们着重讨论为什么系统的同步特性对系统尺寸不敏感。文献[16]指出:在振子环系统中,能量的有限性条件导致了一个共同的修正因子:
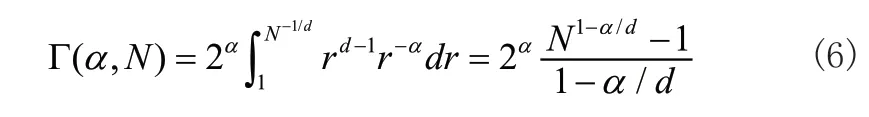
研究发现本文模型中的归一化常数与此处的修正因子是等价的。图4(a)证实:在误差允许的范围内,这两个因子是可以互换的。为了细致的刻画它们之间的差异,我们引入相对偏差,其定义式为:

图4(b)显示,两者的相对偏差在α变化的整个区间内均小于4%。归一化常数与修正因子的等价性,抹平了系统的同步特性对系统尺寸的依赖性。

图4 归一化常数与修正因子的等价性。(a)归一化常数与修正因子呈线性关系;(b)相对偏差曲线。
3 结束语
本文利用尺度变换给出了具有长程幂律相互作用的非线性振子环的临界耦合强度的分析解。研究结果表明:临界耦合强度虽然对系统尺寸并不敏感,但是对随距离衰减的幂律指数有很强的依赖性。这为人们研究幂律指数对振子网络同步动力学行为的影响迈出了第一步。
