半航空瞬变电磁L1范数自适应正则化反演
2021-10-23何可郭明胡章荣易国财王仕兴
何可,郭明,胡章荣,易国财,王仕兴
(1.西华师范大学 教育信息技术中心,四川 南充 637002; 2.成都理工大学 地球物理学院,四川 成都 610059)
0 引言
半航空瞬变电磁法(semi-airborne transient electromagnetic,SATEM)采用接地长导线源向地下供给阶跃电流,使用无人机搭载接收线圈进行空中观测,接收二次场[1]。半航空瞬变电磁法与航空瞬变电磁法相比,具有信噪比高、勘探深度大等特点[2];与地面瞬变电磁比较,具有快速、大面积在复杂地形进行探测的能力,对良导体探测效果较好[3-5]。半航空瞬变电磁法数据量大,相较于航空瞬变电磁采用CDI快速成像,由于需考虑线源长度、偏移距等影响,实现难度大,而三维反演由于计算时间较长,目前也很难在实际中应用,所以实践中数据处理仍以一维反演为主。地面瞬变电磁反演研究主要以“烟圈”理论和最优化算法为主[6-7]。“烟圈”算法快速、近似,适合作现场解释工作[8],但由于不能提供层厚信息,所以只能作为定性研究。最优化算法主要以阻尼最小二乘[9-11]和以Occam反演[12-13]引入模型正则化[14-16]的思想为主,阻尼最小二乘法通过改变阻尼因子大小使算法向高斯-牛顿方向或最速下降方向靠近,改进了最小二乘法收敛不稳定的特性,该方法对初始模型仍然有较高要求,对复杂模型可能出现结果不收敛等现象;Occam反演属于一种L2范数的正则化反演算法,最为稳定,但也主要有两个方面的不足,一是计算时间较长,每次迭代都需要通过多次正演搜索最佳的正则因子,二是反演结果过于光滑,对真实电性界面分辨不足。许多学者对正则化因子的选取作出改进并提出一些新方法,如:采用牛顿迭代法和二分法组合[17]降低正则因子搜索的正演次数;陈小斌等[18]提出MD和CMD两种正则化因子自适应调整方案,应用较为广泛。常规正则化反演算法正则项通常采用L2范数,利用L2范数对电阻率模型进行处理,其假定模型空间分布连续光滑,反演结果会弱化对突变电性界面的分辨能力。国外已有学者在重力、地震数据三维反演[19-20]中采用L1正则项,国内在航空电磁数据反演[21]、三维大地电磁反演[22]中,有学者采用L1正则项来提高反演算法对层状电性介质层界面的分辨率。作为L1范数的一种特例,聚焦反演[23-25]已成熟应用于大地电磁[26]、重力、磁测等[27-28]研究方向,常规的聚焦反演采用NLCG(非线性共轭梯度)直接求解目标函数,然而正则项求解不可靠,容易陷入奇异系数解“陷阱”[22]。
本文正则项采用L1范数,分析了模型在解空间获得稀疏解的原因,采用迭代重加权最小二乘法将原问题转化为L2正则化子问题求解,解决L1范数存在不可导问题,并将两种算法与Occam反演算法结果进行比较;采用OpenMP并行策略对雅克比矩阵进行并行运算,提高反演效率;对分段迭代法自适应正则化因子调整策略进行分析并改进,改进后的自适应正则化因子调整策略更适合半航空瞬变电磁法,通过与Occam反演对比,L1正则反演结果的模型分辨率要优于Occam反演结果。
1 半航空瞬变电磁一维正演
长导线源半航空瞬变电磁法以有限长接地导线作为发射端,不能用电偶极子近似表示,需要沿导线进行积分,对X、Y、Z三个分量均可观测,目前以垂直地面Z分量为主。假设线源中心为笛卡尔坐标系原点,x轴为长导线方向,z轴向上为正,水平层状介质频率域Hz分量公式为[27]
(1)
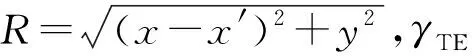
2 L1正则反演理论
2.1 L1正则反演基本原理
常规L2正则化反演目标函数可表示为
(2)
式中:Φ(M)L2为总目标函数;右边第一项为时间域数据拟合项,dobs为观测数据向量,F(M)为理论正演响应,M为模型参数向量,有n个元素,每个元素均为电阻率自然对数;Wd为数据加权矩阵,一般为主对角矩阵,其元素为观测数据噪声的倒数;第二项为L2正则模型约束项,Mref为参考模型,可取CDI成像结果为参考模型或者以均匀半空间为参考模型,超参数λ为正则化因子,其控制反演更倾向于拟合数据或参考模型,Wm为数据加权矩阵,一般可取最小模型约束(单位算子)、最平缓模型约束(梯度算子)、最光滑模型约束(拉普拉斯算子),本文采用模型约束项为:
L1正则反演目标函数为:
λ‖Wm[Mref-M]‖1。
(3)
对式(2)和式(3),可以用如下形式表示:
(4)
(5)
L2范数是向量各元素平方和开方,具有连续光滑的特点[21],这也使得代表层状介质模型各分层电性结构的最终结果呈连续变化,不能明显刻画各层界面。L1范数是指向量各元素mi绝对值之和,也称为“稀疏规则算子”,其向量中部分元素与最终输出没有任何关系或不提供任何信息,可以允许电性介面发生陡变。最小化目标函数的时候考虑mi这些额外特征虽然可以获得最小误差,但是也将部分无用信息考虑进去,使得对模型增量的判断有所偏差,稀疏算子可以去掉无用信息,将其权重置为零。
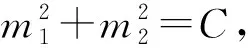
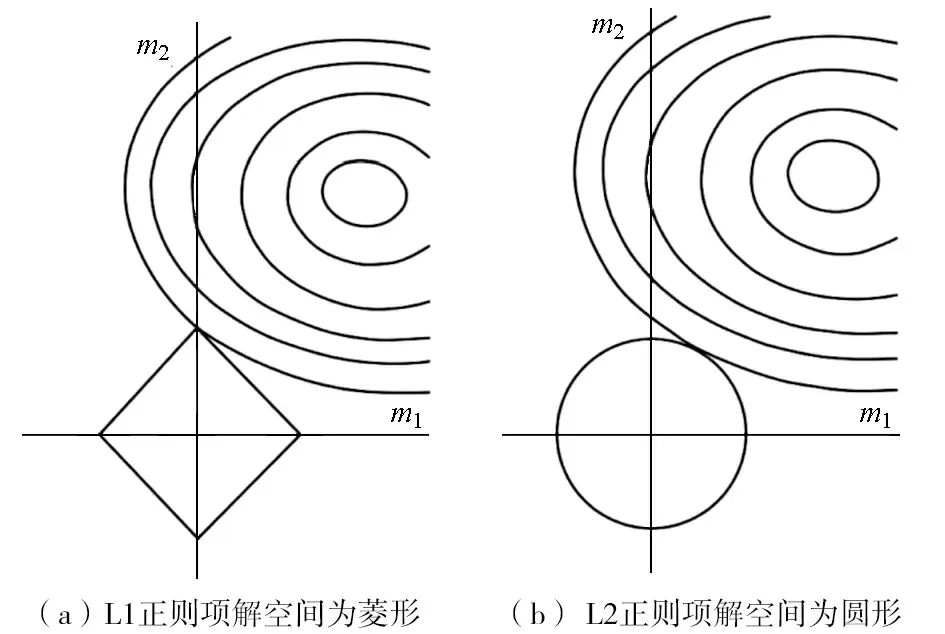
图1 数据拟合项与模型约束项等值线Fig.1 Contour plots of data fitting items and model constraints
众所周知,L1范数取绝对值在存在不可导情况下会使迭代不稳定,L1范数正则项最速下降方向无法得到。可取一个小值ξ,将式(5)改写为
随着网络时代的发展,出现了大量老年教育网站,老年人可以通过网络学习、交友、娱乐等。通过对温州老年人学习网、夕阳红·江苏老年学习网、山东老年大学远程教育网、老年开放大学等18家国内主流老年教育网站调研,发现存在课程资源缺乏老年特色,这些网站多数不能多终端共享,老年远程教育网站缺乏真正的交互设计等问题。
(6)
针对正则项存在不可导问题,采用迭代重加权最小二乘法(IRLS),将正则项改写为
(7)
式中:V为对角加权矩阵,主对角线上元素为:
(8)
对式(6)关于增量Δmk(下降方向)求导:
(9)
式(9)右边第一项为数据拟合梯度项,第二项为正则梯度项,Jk为雅可比矩阵(与正演贝塞尔函数无关)。
2.2 自适应正则因子策略
关于正则化因子的调整,陈小斌等[18]提出了MD和CMD两种方案。
MD方案:
(10)
CMD方案:
(11)
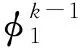
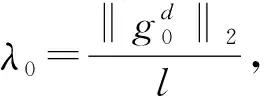
>5%,
(12)
则有λk=λk-1,否则λk=λk-1/ω。这里引入了另一个超参数ω[22],ω需取适当的值才能达到比较好的效果。由于在没有先验信息情况下设置参考模型,Mref设为均匀半空间模型时正则因子初始值过大,模型增量较小,所以前几次迭代模型几乎不发生改变。随着迭代时间和次数增加,对其作一定改进,使初始正则化因子处于一个较小的值,再按照适当比例逐渐衰减,过程如下。
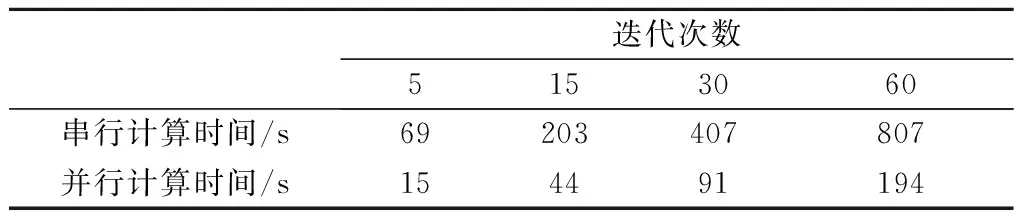
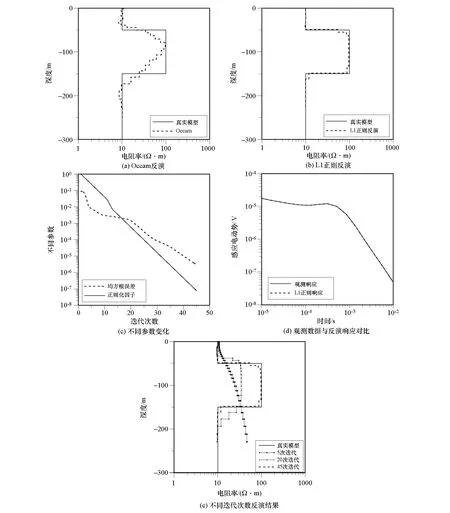
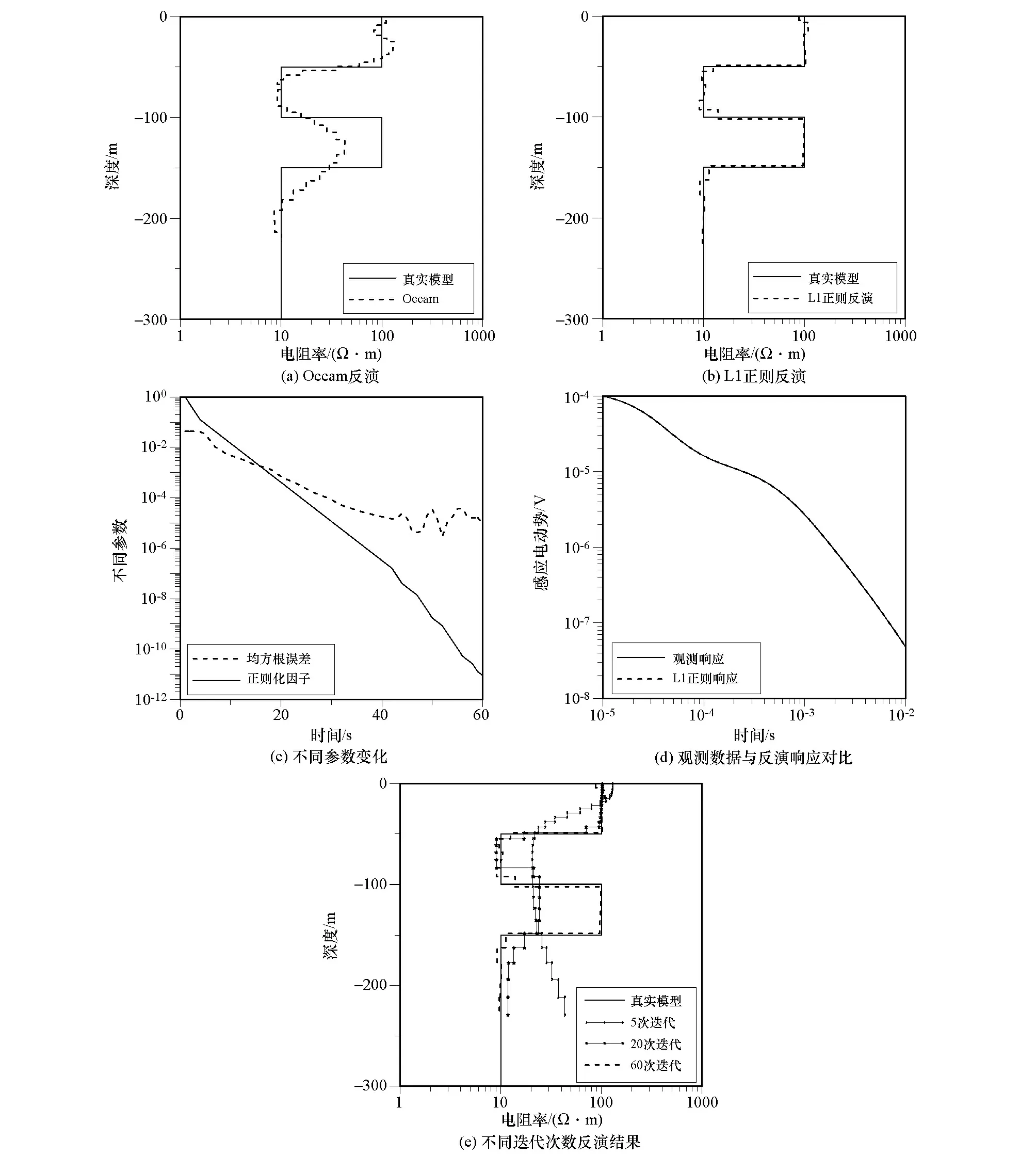
设定反演结束条件为:①达到最大迭代次数;②相邻两次拟合差小于给定拟合误差(Rms1-Rms2 (13) OpenMP是一种共享内存系统的多处理器多线程并行语言[36],采用fork-join(分叉—合并)并行执行模式。主线程作串行运算,当遇到并行模块时,调用其他从线程构成线程组,同时访问共享内存区域,执行命令,执行完毕跳出并行区域,继续执行串行命令。OpenMP并行策略具有效率高、执行快的特点,适合单机操作。 半航空瞬变电磁反演耗时主要在于雅克比矩阵求解时需要多次调用正演,采用二维数组存储雅可比矩阵,形成二重循环,主要运算时间也集中在内循环(每一行)参数的正演计算,参数越多耗时越长。OpenMP可以对嵌套循环体内多个循环进行并行运算,本文采用如图2所示方案,只对内循环进行并行运算策略,对循环内变量作无关处理,各线程对数据、函数的调用相对独立。本文用3层模型进行试算,观测值15道,初始模型为30层均匀半空间;计算机处理器为Intel(R) Core(MT)i5-8265U,主频 1.6 GHz,4核8线程,分别进行5次、15次、30次、60次迭代,计算时间对比如表1所示,采用并行运算后,运算时间约缩短3/4,效率显著提高。 图2 OpenMP运算并行策略Fig.2 OpenMP computing parallel strategy 表1 串并行计算时间对比 设定半航空瞬变电磁参数如下:线源长度1 km,电流20 A,线圈接收高度20 m,线圈面积为1,偏移距为250 m,即测点坐标为(0,250,20);设初始模型30层,初始层厚为2 m,依次递增,每层电阻率为50 Ω·m,对理论模型响应值均加入3%的高斯白噪声,并与Occam反演结果相比较。 3.1.1 H型模型反演 H型模型初始电阻率由浅至深分别为100、10、100 Ω·m,对应层厚分别为50、50 m,最后一层层厚设为无穷大。其不同方法反演结果见图3。 由图3a可见,Occam反演结果较为光滑,对分界面刻画较弱,第一、二层电阻率值与真实模型对比有所偏离。图3b中,L1正则反演结果对各层分界面刻画清晰,电阻率值和层厚更接近真实模型。图3c显示了反演算法拟合差和正则化因子衰减过程,迭代较为平稳。图3d为观测数据与反演拟合响应的对比,数据拟合较好,接近真实值。图3e中可以看出第5次迭代时趋向于L2范数反演结果,随着迭代次数增加,对角加权矩阵V变得更复杂,层界面刻画逐渐清晰。第15次迭代时电阻率值接近真实模型,层界面刻画较为准确,第35次迭代时达到拟合条件,与真实模型接近。 图3 H形模型反演结果Fig.3 Inversion results of H-shaped model 3.1.2 K型模型反演 对K型模型,电阻率设为10、100、10 Ω·m,对应层厚分别为50、100 m,最后一层设为无穷大半空间。图4a、图4b显示Occam和L1范数这两种算法都能有效反映出高阻部分,但Occam反演在层厚较大时对层界面的刻画更为光滑,第一层和第三层的电阻率值与真实模型比较出现较小偏差,而L1范数对层界面刻画清晰, 电阻率值更接近真实模型。从图4e可以看出,第20次迭代时基本能反映出层状介质的基本模型;通过和H型反演迭代次数比较,可以看出对高阻的拟合相对困难,迭代次数增加。 图4 K形模型反演结果Fig.4 Inversion results of K-shaped model 四层层状模型电阻率设为100、10、100、10 Ω·m,对应层厚分别为50、50、50 m,最后一层设为无穷。如图5所示,总体结果与图4结论相似,可以看出随模型的复杂程度增加,迭代次数也随之增加。本次拟合2种反演方法都迭代在60次左右,Occam反演低阻拟合较好,对第三层的高阻部分拟合较差;L1正则反演对层界面位置反应与真实模型吻合较好,同时电阻率值也接近真实模型,说明L1正则反演方法相对于Occam反演对高阻的反应相对灵敏。随着模型的复杂度变高,反演迭代次数也随之增加,正则化因子较小时约束减弱,拟合差也有波动现象。然而,实际工作过程中并不知道地下实际电性结构分布,但L1正则反演在一定迭代次数后可以反映出层状介质大致模型,所以可以根据实际地质情况调整反演约束条件。 图5 HK形模型反演结果Fig.5 Inversion results of HK-shaped model 针对半航空瞬变电磁L2正则反演层界面刻画不够清晰的问题,提出了利用L1正则反演处理半航空瞬变电磁数据,对自适应正则化因子调整策略进行改进优化,并用三层的H、K地电模型和四层的HK型地电模型对两种反演算法进行了试算与比较,通过分析得到以下结论: 1)基于L1范数的正则化反演算法比L2更有利于得到稀疏解,允许模型电阻率在空间分布上存在尖锐;对层界面位置反映较好,相对复杂的层状介质模型也能得到较好的反演效果;对高阻的分辨率也较高。 2)L1范数正则项采用迭代重加权最小二乘法,解决了不可导问题,反演结果早期趋向于L2范数反演结果,随着迭代次数增加,对层界面的分辨逐渐清晰;正则化因子分段迭代法中比例因子的选取会影响收敛速度,因子越大迭代越稳定,但收敛较慢。 3)正则化因子采用分段迭带法,和OpenMP并行策略使得反演较快,然而相较于Occam通过搜索方式得到的正则化因子不是最优的,面对复杂模型的反演时可能会出现假异常。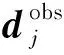
2.3 OpenMP并行策略

3 理论模型反演分析
3.1 三层模型反演算例

3.2 四层HK型模型反演算例
4 总结
