Lebus 卷筒钢丝绳缠绕性能分析与仿真

戴小琴 施 湧 刘兆航 熊茂源 孙远韬

1 上海振华重工（集团）股份有限公司 上海 200125 2 同济大学机械与能源工程学院 上海 201804

0 引言

随着集装箱船舶大型化的发展，岸边集装箱起重机（以下简称岸桥）的前伸距越来越大，故需要直径更大、长度更长的卷筒，更大的减速器、电机等驱动部件。同时安置俯仰机构的机房也需加大，给岸桥的大型化带来轮压大、稳定性差、能耗大、建造成本和维修成本高等劣势。在设计大型岸桥机构时，采用单层缠绕的卷筒已不能满足使用要求。故为了跟随岸桥3E 化（规模经济Economy of scale、能源效率Energy efficient 和环保绩效Environmentally improved)的趋势，能自动实现整齐、规则的多层缠绕的钢丝绳卷筒是高速、重载类卷扬设备的发展趋势。自Lebus 先生发明了折线卷筒，其基本结构形式保持至今，依靠圆周段下层钢丝绳形成的槽对上层钢丝绳的双侧约束实现多层缠绕的定位，依靠卷筒两端端板和爬台辅助钢丝绳的爬升和自动换向。为了更好地实现整齐、规则的多层缠绕，大量研究人员对相邻绳槽中心距、绳槽圆周段与螺旋段的比例、爬台形式和尺寸等进行深入研究，以保证自动爬升与换向功能的实现[1-5]。

综合国内外关于Lebus 卷筒所涉及问题的研究现状，本文从Lebus的缠绕关键失效过程出发，分析了可能出现的乱绳现象，根据缠绕过程中自动换向运动阶段特点和理想爬坡缠绕模式，建立爬台关键点轨迹方程，并和常用的阿基米德螺旋线通过Matlab 仿真进行比较，说明改进的方向，然后通过缠绕过程的ADAMS 仿真说明所设计爬台的合理性。

2 缠绕关键过程失效分析

Lebus 卷筒在缠绕过程中，钢丝绳在圆周运动区受到绳槽的双侧约束，得以较好地定位，不易乱绳。而在螺旋运动区钢丝绳在轴向上是自由的，尤其是第二层绳以上每层的第一圈绳，一侧受端板约束，另一侧位置由受力情况确定。理想的缠绕是指钢丝绳按设定轨迹缠绕，实际缠绕轨迹偏离理想轨迹达到一定程度，则认为缠绕失效，即发生乱绳。每一层首圈的自动换向过程是缠绕的关键过程，当此过程符合理想轨迹，则同一层第二圈及之后的绳圈即有了准确的导向要素，同时也为上一层的钢丝绳提供了定位基础。整个缠绕是一个递推的过程，前面的绳缠绕整齐是后面的绳得以继续规则缠绕的基础[6]。

在钢丝绳缠绕中，卷筒的结构特点作为内因，钢丝绳所受载荷作为外因，共同作用影响钢丝绳的缠绕性能。对钢丝绳缠绕各阶段导向因素分析可知：卷筒绳槽为底层钢丝绳提供了可靠的约束；第二层及以上的钢丝绳圆周运动区，由下层钢丝绳形成的绳槽提供了定位约束；爬升过程与每层第一次换向过程的导向因素均为下层钢丝绳的挤压力和端板的挤压力；每层第二圈后的钢丝绳缠绕的主导向因素为其同一层已缠绕相邻绳的挤压力。

如图1 所示，自动换向运动阶段的起点是圆周运动区的终点，此时钢丝绳从卷筒伸出经导向滑轮与吊具相连，若将滑轮与卷筒带槽部分的中间面对齐，则钢丝绳到达卷筒两端时出绳具有一定角度α。因此，绳的运动趋势与卷筒轴线成锐角，偏离卷筒端板，换向阶段的起点出绳角恰好为α，钢丝绳张力Fs具有轴向分量Fy。图2 是跨绳换向过程3 个主要位置在垂直于卷筒轴线平面上的投影。跨绳起点时刻钢丝绳与下层2 个绳圈同时相切，处于2 绳圈形成的槽中，在位置Ⅰ，换向过程的设定轨迹为沿着与底层旋向相反的方向缠绕，则钢丝绳需跨过底层绳，即经过位置Ⅱ，再回落到与位置Ⅰ同等高度的位置Ⅲ。而位置Ⅱ处于最高点不稳定，绳受到扰动即滑落。若钢丝绳恰好落入相邻槽且未使绳产生强烈振荡，则缠绕理想。现从能量的角度分析典型缠绕过程以分析影响缠绕性能的因素。

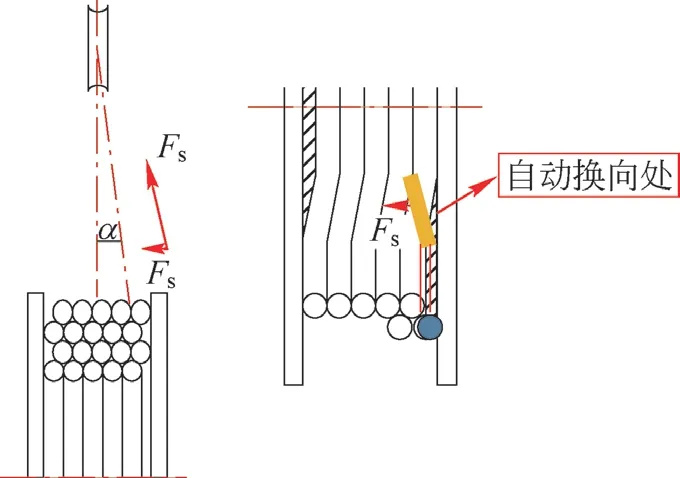
图1 自动换向位置

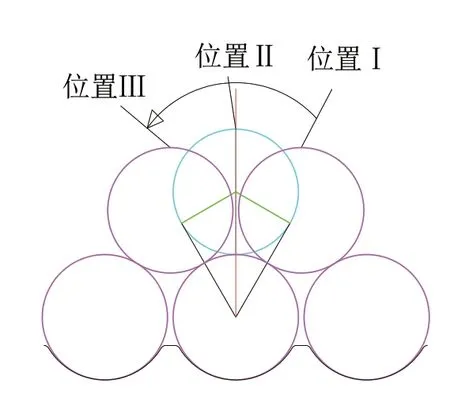
图2 自动换向过程绳的3 个状态图

换向过程是钢丝绳沿卷筒轴向运动与径向运动的合成运动，理想缠绕轨迹是螺旋运动区的绳段在径向运动的同时轴向跨过1 个绳槽。如图3 所示为第2 层钢丝绳首圈自动换向过程的关键位置Ⅰ～位置Ⅲ，A1与B1表示第1 层绳，A2与B2表示第2 层绳，第1 层为右旋绳，第2 层为左旋绳；设卷筒轴向为坐标系的x轴，径向设为y轴。轴向位移x与重心升高量是周向缠绕角度的线性函数。而实际缠绕时如果条件不当，有可能出现图4 中的2 种乱绳情况。

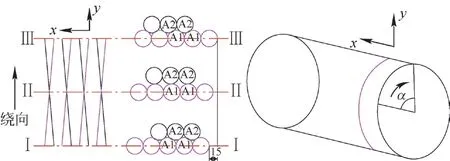
图3 正常缠绕的位置示意图

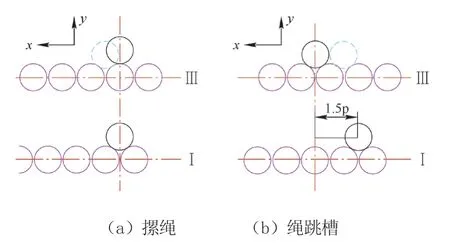
图4 2 种乱绳情况示意图

在正常缠绕、摞绳、绳跳槽3 种情况下，由于绳段均沿径向抬高，势能都增大，分别分析3 种情况的势能变化，能量越低的状态越稳定。

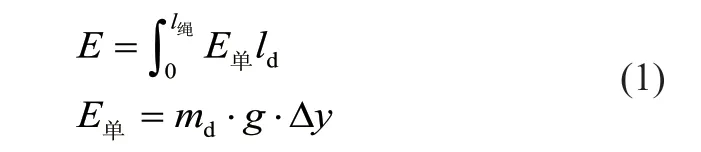
式中：md为将绳子离散成均匀的多段单位绳段，单位绳段的质量；Δy为任意时刻绳段重心升高量；E单为单位绳段的势能增加量；l绳为螺旋运动区总绳长；ld单位绳长；E为总势能增加量。

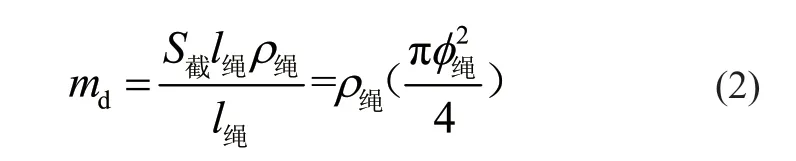
式中：S截为绳的截面面积，ρ绳为绳的密度。

1）正常绕绳 如图3 所示，绕绳正常时，从位置Ⅰ到位置Ⅱ绳段重心逐渐抬高，势能增加；从位置Ⅱ到位置Ⅲ绳段重心逐渐降低，势能减少；当到达位置Ⅱ时，处于最高点，此时绳段重心抬高量为

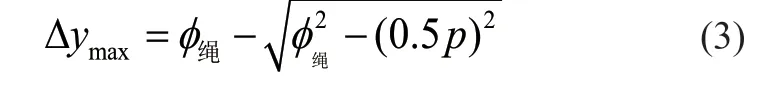
从位置Ⅰ～位置Ⅲ，绳圈B 轴向运动了0.5p，周向运动了α0，如图5 所示。从位置Ⅰ～位置Ⅱ和从位置Ⅱ～位置Ⅲ是对称过程，故势能和为E=2EⅠ～Ⅱ，只须计算缠绕0.5α总的过程。

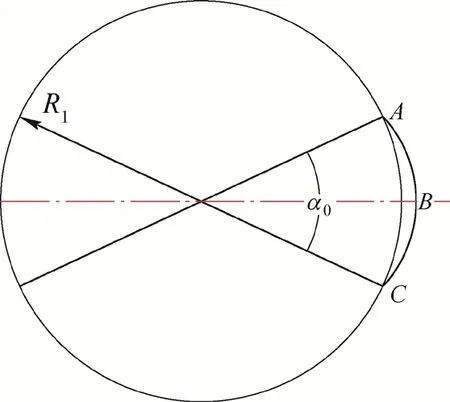
图5 垂直于卷筒轴线的视图

以位置Ⅰ为起点，从位置Ⅰ运动到位置Ⅱ的任意时刻，设绳段周向缠绕角度为αt，则绳段中心在该时刻的重心升高量为

忽略重心运动变化带来的绳长变化，固有绳长与缠绕角度之间的关系为

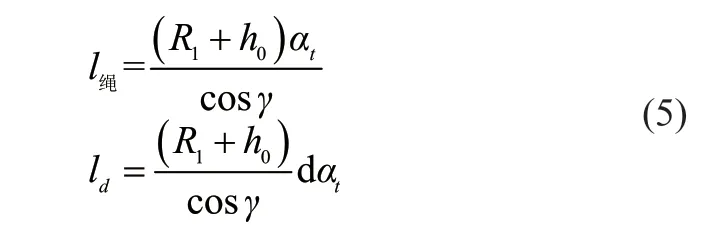
式中：γ为螺旋运动区的螺旋升角（见图6），R1为底层缠绕半径，h0为层间距。

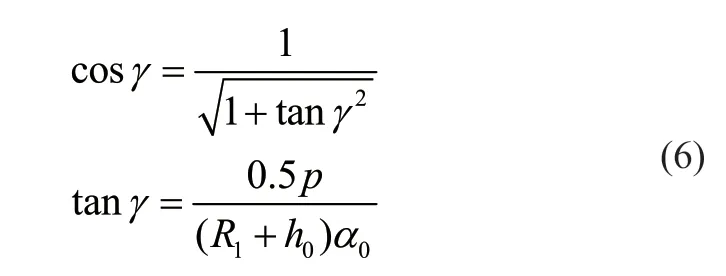
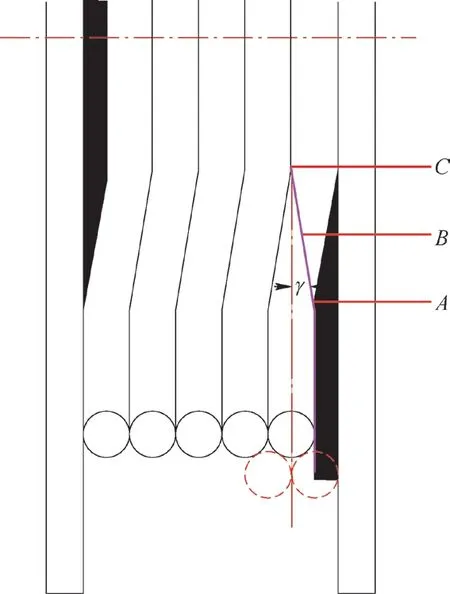
图6 卷筒展开图

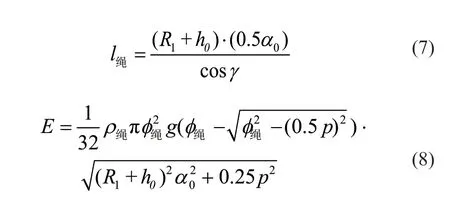
2）摞绳 图4a 为上层钢丝绳未发生轴向偏移，x=0，螺旋区总势能增加

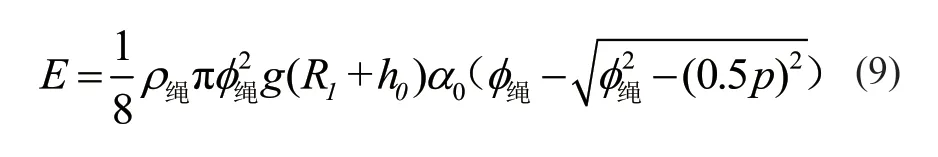
3）跳槽 图4b 为钢丝绳在自动换向阶段轴向位移过大时，终点处越过了与起点相邻的绳槽发生乱绳。绳缠绕α0的过程中轴向移动了1.5p，与下层2 个绳圈均有交叉点。2 交叉点之间的绳段重心抬高量始终为Δy=Δymax，即保持最高点平移；而起点与交叉点1 之间、交叉点2 与起点之间轴向位移x与周向缠绕角度αt为线性关系，设螺旋区α0内总绳长为l绳，跳槽过程绳段增加的总势能为

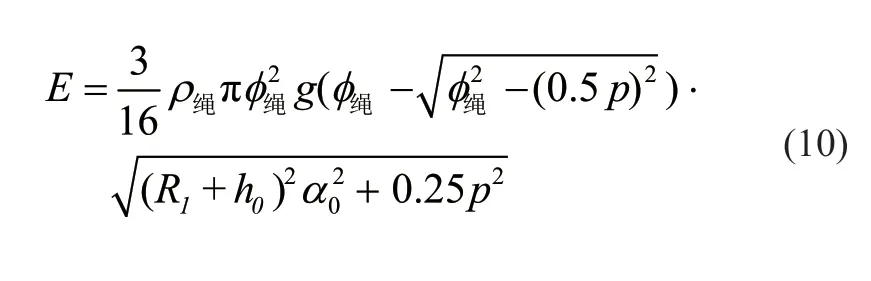
对比3 种情况势能增加的大小，可知其中正常缠绕时势能增加最小，跳绳时势能增加最大，即正常缠绕时系统的能量最低、最稳定。发生摞绳时，轻微的干扰将使得绳段整体发生轴向位移，掉入距离其最近的槽中，形成螺旋运动区的理想缠绕轨迹；发生越槽时，由于钢丝绳在螺旋区的终点处于下层绳形成的槽中，受到双侧约束，可继续缠绕，然而将为后面的绳圈以及上一层的绳圈提供错误的导向，引起后绕绳乱绳，故亦处于不稳定状态。对于钢丝绳换向中3 种情况的能量分析，有利于理解Lebus 卷筒各设计参数以及工作条件对于钢丝绳缠绕的影响，对于Lebus 卷筒参数设计以及使用提供指导意见。

3 理想钢丝绳爬升模式

3.1 爬台理想轨迹分析

爬台的主要功能是辅助钢丝绳爬升到新一层的高度与其在螺旋段自动换向缠绕，由于双折线卷筒的下层钢丝绳会为上层钢丝绳提供约束与导向作用，一般情况下，当第1 层与第2 层钢丝绳完全按照理想轨迹缠绕，则上层绳的缠绕性能即可得到保证，故只要爬台能够辅助钢丝绳完成第1 层到第2 层的爬升及第2 层首圈的首次换向即可。而在钢丝绳首层爬升过程中，如果没有爬台，钢丝绳挤在下层钢丝绳与挡环间不断缩小的间隙中被迫抬升，必然引起钢丝绳的挤压磨损，影响钢丝绳的使用寿命。合理的Lebus 卷筒爬台是保证钢丝绳正常缠绕的关键，同时对于减小钢丝绳摩擦，延长使用寿命有着重要意义[7-9]。

3.2 理想钢丝绳爬升模式

爬升过渡段正在爬层的钢丝绳与先绕的相邻绳圈和端板始终相切，是爬台设计的先决条件。爬台实质是对于爬升钢丝绳、相邻绳圈以及端板之间间隙的补充，完成辅助爬升的功能。理想爬台曲面应如图7a 所示[10]，只有保证爬升钢丝绳圈（B 圈）同时与第1 层最后一圈钢丝绳（即相邻的A 圈）、爬台面以及卷筒挡盘内端面（H面）三者相切，才能使钢丝绳顺利地爬上第2 层。

如果爬升钢丝绳绳与三者任一不相切，都会影响钢丝绳在过渡层上的理想缠绕，可能出现的情况如图7b、图7c、图7e 所示。如图7b 所示的爬台过高为缠绕发出噪声的主要原因；图7c 为爬台过宽导致的过卷现象；图7e 为爬台过低导致钢丝绳切入首层末圈绳与卷筒挡盘的间隙中，是目前大部分卷筒会发生的情况。

根据理想爬坡缠绕模式，建立爬台关键点轨迹方程：

1）与爬升钢丝绳接触点的轨迹方程

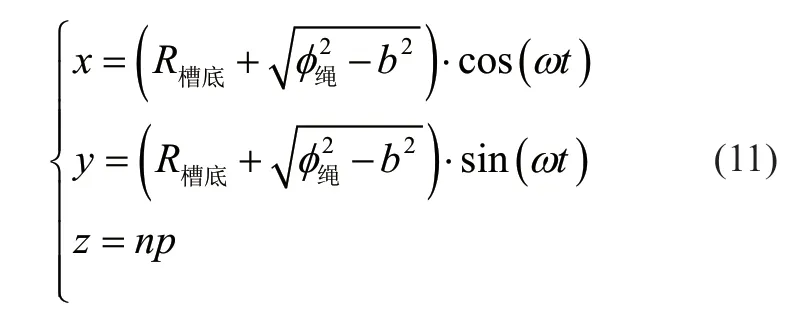
2）与第1 层最后一圈钢丝绳接触点的轨迹方程

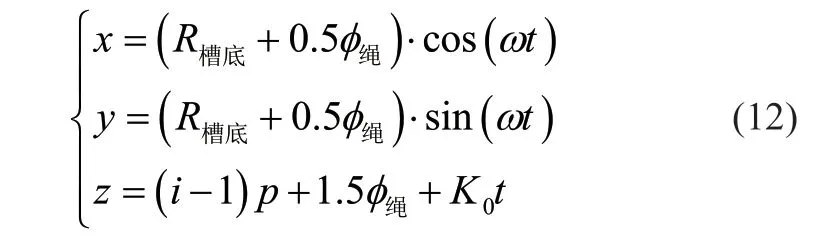
与第1 层最后一圈钢丝绳接触点的轨迹决定了爬台的宽度；与爬升钢丝绳接触点的轨迹决定了爬台的高度。

3.3 爬台的高度与宽度尺寸

如图8 所示，虚线的两圆是钢丝绳爬升时的起始位置，随着钢丝绳进一步爬升，爬台宽度减小，高度升高，钢丝绳被迫爬升，并在爬升过程中保持与第1 层最后一圈钢丝绳、爬台面以及卷筒挡盘内端面三者相切。图8中两圆O1和O2是钢丝绳爬升过程中的某一位置，O即为钢丝绳圆心O2被爬升时的起始位置。图8 中阴影部分为爬台，设此时对应圆心角为θ，间隙宽度为b，爬台的理论高度为h，由图中可知。

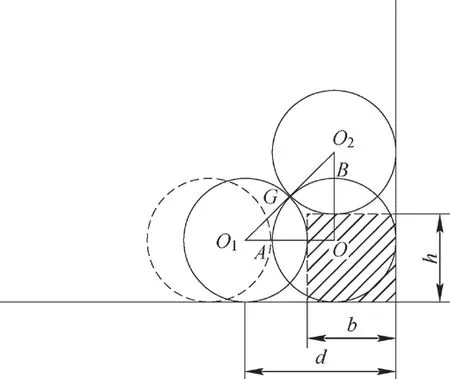
图8 接触点示意图

如图9 所示，整个缠绕过程共分为3 部分：螺旋区2、圆周区2 和螺旋区1。

缬沙坦联合丹参川芎嗪治疗高血压合并糖尿病的疗效观察…………………………………… 陈 琳，朱 燕（3·211）

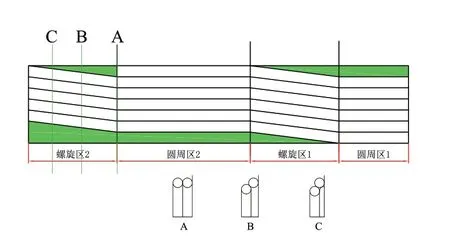
图9 爬升区钢丝绳缠绕示意图

1）当φ绳≥b≥φ绳/2 时（螺旋区2）

对卷筒爬台，0°≤α1≤54°

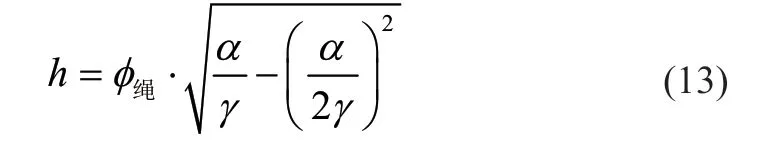
宽度b在爬升折线区为均匀变化

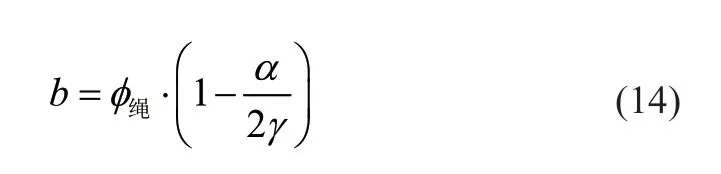
2）当b=φ绳/2 时（圆周区2）

对卷筒爬台，0°≤α2≤126°

3）当φ绳/2 ≥b≥0 时（螺旋区1），此段爬台并不与钢丝绳接触，不影响钢丝绳缠绕的性能。

4 仿真分析

4.1 Matlab 爬台形状仿真

目前了解到常见卷筒爬台多采用阿基米德螺旋线简化爬台，对理想爬台曲线和阿基米德螺旋线进行Matlab仿真，说明2 种曲线的差别以及需做出的改进。

使用阿基米德螺旋线，则爬台高度为

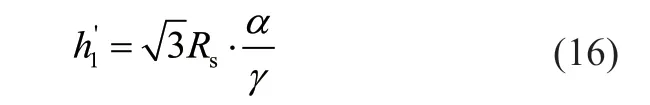
2 条曲线高度对比如图10 所示。直接使用阿基米德螺旋线简化爬台，在爬升区中间段，钢丝绳与爬台之间有较大的间隙，此时爬台不能帮助钢丝绳爬升。故应考虑其他曲线代替理想曲线。

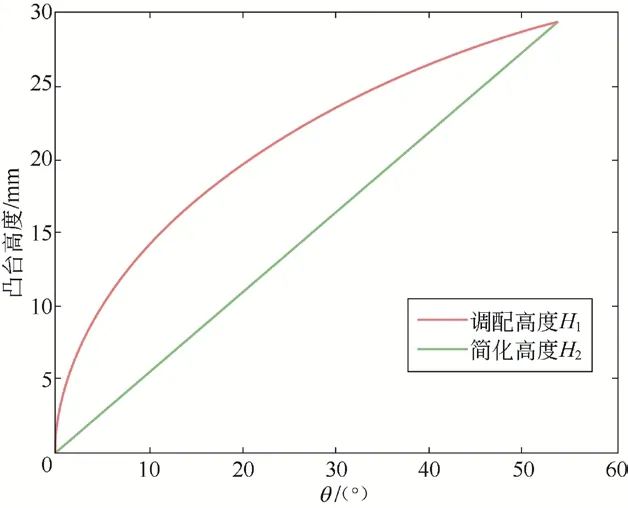
图10 爬台理想高度曲线图与简化高度曲线

采用3 次多项式近似爬台曲线，最终优化为

优化后的结果与理想值的比较如表1 所示。由表可知，该曲线的最大误差为2.81%，满足爬台设计要求。

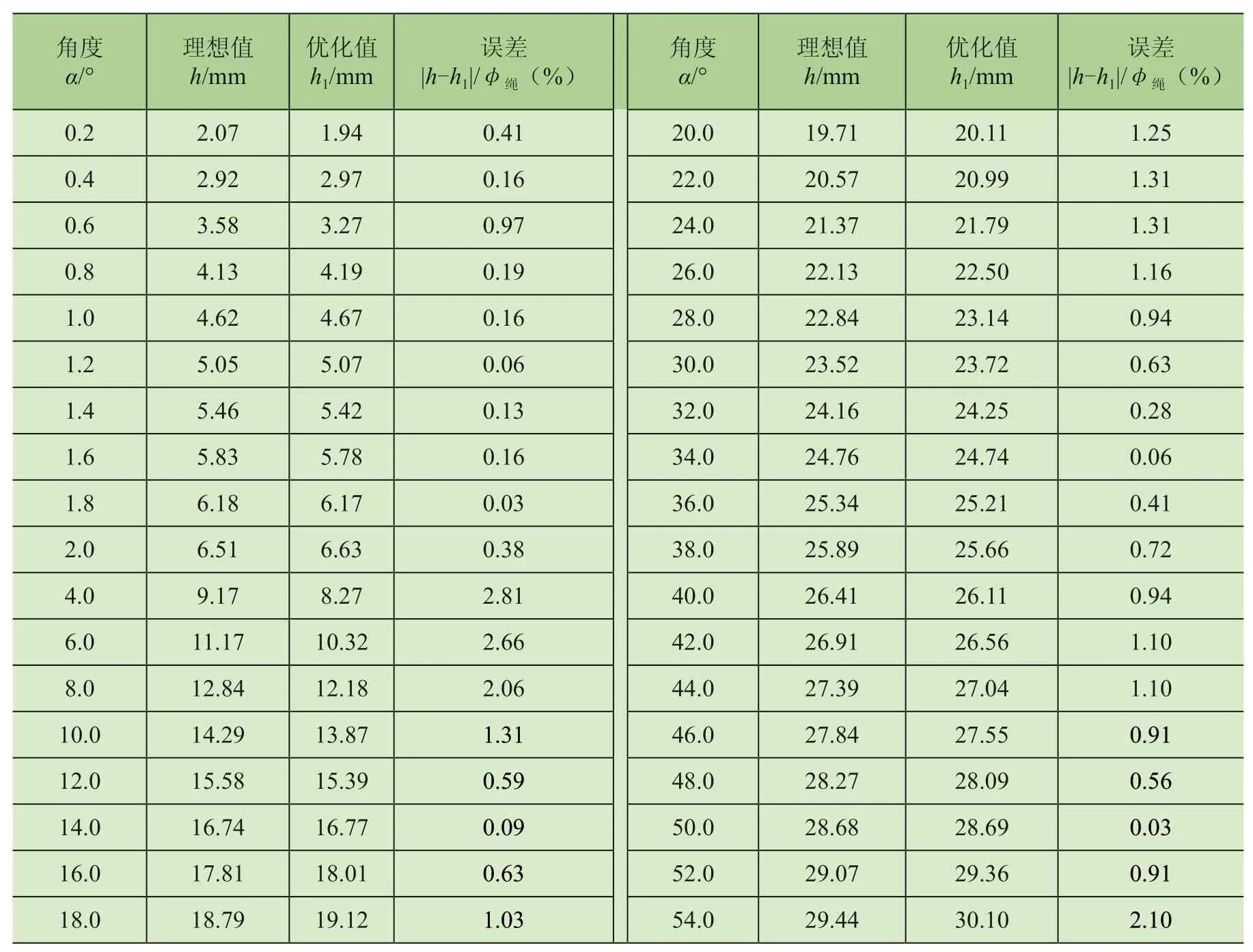
表1 爬台的原始高度及优化高度

4.2 ADAMS 优化爬台爬升仿真

绳索挠性好，尺寸上的几何非线性等特点，自身的刚度系数、阻尼系数、接触刚度系数、接触阻尼系数难以确定，是多体动力学仿真中的难点。现有主要的模拟方法有2 种[11]：半连续法（多刚体法）、离散法（相对节点法）。

多刚体法的基本思路是将绳索划分为若干小段圆柱体，每个圆柱体为刚体，每段圆柱体的长度与绳子全长相比很小，各个刚体小段的质心在任意时刻的运动学参数（位移、速度、加速度）和物理参数（受力情况、转动惯量等）以及2 个刚体间的动力学参数（相对位移、相对转角、相互作用力与反作用力等）同实际绳索物体的相应值尽可能相似，则该多刚体组合模型可近似代替绳索。[12-16]

在ADAMS 中建立优化爬台模型，完成钢丝绳爬升动作过程仿真模拟，如图11、图12 所示。ADAMS 仿真结果如图13 所示。

图11 卷筒模型

图12 爬台细节示意

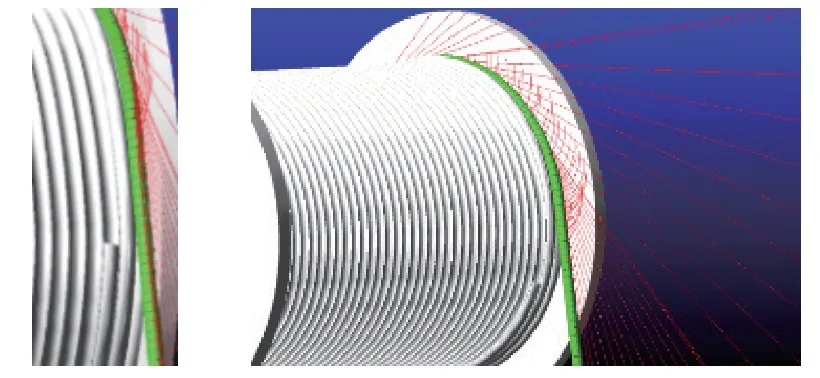
图13 ADAMS 仿真结果

在仿真过程中，钢丝绳成功完成爬升缠绕过程，证明得到的3 次多项式优化爬台曲线具有良好的辅助爬升功能。

5 结论

1) 研究分析了Lebus 缠绕失效过程，用能量法说明了正常缠绕、摞绳、绳跳槽的特征方程。

2) 对爬台理想轨迹进行了分析，并将理想爬台曲线与阿基米德螺旋线进行Matlab 仿真，说明2 种曲线的差别，提出用3 次多项式拟合的方法来制造爬台。

3) 利用ADAMS 绳索单元模拟了Lebus 卷筒缠绕过程，说明所建立卷筒特别是爬台部分用3 次多项式进行拟合的合理性。