一类时滞脉冲随机系统的有限时间稳定性
2021-10-23李羽辰姚凤麒
李羽辰,姚凤麒
(安徽工业大学 电气与信息工程学院,安徽 马鞍山 243032)
众所周知,经典的Lyapunov稳定描述了系统在无穷时间内的渐进特征[1]。然而,它只反映了系统的稳态性能,并不能反映系统的调节时间、峰值时间、超调量等暂态特性[2]。这在实际工程中并不适用,如网络通信系统、火箭发射系统、高精度机械臂等,都需要系统满足一定的暂态性能要求[3]。因此,20世纪60年代就提出了有限时间稳定(FTS)的概念。有限时间稳定性是指当系统的初始状态在一定范围内时,系统的状态在一定时间间隔内不超过预定的限度[4-6]。本文结合实际,考虑了随处可见的时滞对系统的影响,并引入了脉冲控制,构建了一个Lyapunov-Krasovskii泛函,得到系统的有限时间均方稳定性能,最后通过Matlab,验证了结论的有效性。
符号说明:Rn代表n维欧式空间,N代表非负整数集,E[·]为数学期望算子,diag{·}代表对角矩阵,λmax(A)(λmin(A))代表矩阵A的最大(最小)特征值,A>0代表A是正定矩阵,A<0代表A是负定矩阵,*代表矩阵的对称项。
1 预备知识
考虑具有定时滞的线性脉冲随机系统
(1)

定义1 对于给定正常数c1,c2,T,c1 (2) 则称系统(1)关于(c1,c2,T)有限时间均方稳定。 定义2 给定脉冲序列{tk}(k∈N),如果存在正数τa和正整数N0,满足 (3) 则该脉冲序列的平均脉冲区间为τa,N(t,s)代表脉冲序列在时间(t,s)内脉冲发生的次数。 引理1 令u:[t0,∞)→R+满足时滞微分不等式 若η+ξ>0,可得 u(t)≤Me(η+ξ)(t-t0),t∈[t0,T], dx(t)=f(t,x(t))dt+g(t,x(t))dω(t) dV(t,x(t))=LV(t)dt+Vx(t,x)gdω(t)。 (4) 首先,利用Lyapunov-Krasovskii泛函和李雅普诺夫函数,结合时滞微分不等式,建立了系统(1)在u(t)=0下的有限时间均方稳定的充分条件。 定理1 假设脉冲序列满足平均脉冲区间条件,给定正数c1,c2,T(0≤c1 (5) FTPF-μP≤0, (6) (7) (8) 式中:λ1=λmax(P),λ2=λmax(P),λ3=λmin(Q),则系统(1)(u(t)≡0)关于(c1,c2,T)有限时间均方稳定。 证明:选择Lyapunov-Krasovskii泛函 当t≠tk,k∈N时,系统(1)轨迹上的Kolmogorov算子 dV(t)≤αV(t)dt+2xT(t)P[Dx(t)+Ex(t-h)]dw(t) (9) 将式(9)在tk到t上积分并在两边取期望,可得 (10) 由Gronwall 不等式可得 EV(t)≤eα(t-tk)EV(tk),t∈[tk,tk+1),k=0,1,2,…。 (11) 由条件(6)和μ≥1,可得 进一步可得 (12) 令 EV(t)≤μN(t,t0)EV(t0)eα(t-t0),t≥t0。 (13) 当t∈[t0,t1),N(t,t0)=0时,由式(13),可得 EV(t)≤EV(t0)eα(t-t0),t∈[t0,t1), (14) 当t∈[t1,t2),N(t,t0)=1时,利用式(11)、式(12)可得 (15) 类似地,当t∈[t2,t3),N(t,t0)=2时, (16) 所以,通过简单的归纳法说明式(13)成立。因此,结合平均脉冲区间以及μ≥1,由式(13)可得 (17) 对于给定形式的Lyapunov函数V(t),有 (18) 所以,系统(1)(u(t)≡0)是关于(c1,c2,T)有限时间均方稳定的。 考虑时滞脉冲随机系统(1),其系数矩阵如下: 取N0=3,τa=0.24,假设脉冲序列满足假设,如图1所示。 图1 脉冲序列N0=3,τa=0.24 取c1=0.1,c2=10,T=2,h=0.5,μ=1.121 0,α=0.794 1,使用Matlab中的线性矩阵不等式求解定理1中的不等式(5)~不等式(8),得到t<0说明存在可行解,得到 易得矩阵的最大、最小特征值,λ1=102.074 9,λ2=122.594 0,λ3=220.771 4。当系统(1)在u(t)=0时的均方样本轨迹如图2所示。由图2可知,系统(1)在u(t)=0时是关于c1,c2,T有限时间均方稳定的,结论可证。 图2 开环系统的均方状态轨迹 本文研究了一类线性时滞脉冲随机系统的有限时间均方稳定问题。利用Lyapunov稳定性理论、时滞微分不等式和平均脉冲区间方法,利用Matlab中常用的LMI工具箱,建立了有限时间稳定的一些易于验证的充分条件。以本文的方法为基础,可以继续研究具有时变时滞的切换系统有限时间稳定、非线性脉冲随机系统的有限时间同步等课题。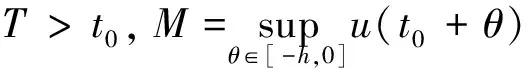



2 有限时间稳定性分析



3 数值算例


4 结 语
