基于属性分组的扩展朴素贝叶斯分类器

王 峻

(淮南师范学院 计算机学院, 安徽 淮南 232001)

朴素贝叶斯分类器[1]是一种简单有效的分类方法，在人工智能、统计决策等领域得到广泛应用。其属性之间相互条件独立的假设，忽略掉了属性间相关性的客观存在。在实际应用中，属性间相关性和属性对分类的影响都不完全相同，使得它的分类性能受到一定的影响。

属性是数据集中最基本的组成部分，属性的选择和属性间的相关性是影响贝叶斯分类器的主要因素，也是改善贝叶斯分类器性能的主要方法。程玉虎等[2]提出一种可变选择性贝叶斯分类器,运用最大相关最小冗余方法选择对分类最有效的属性；徐光美[3]提出运用扩展信息标准选择与分类最相关的属性；李宏磊等[4]提出一种垂直切换算法，以降低因属性条件独立假设而导致的分类性能影响。扩展贝叶斯分类器可以通过添加有向边的方式表达属性间的相关性，例如Friedman等[5]提出一种TAN分类器，每个属性可以拥有一个非类别的父结点，通过添加有向边的方式，按照树型结构的形式将属性与非类别的父结点的相关性表达出来。Cheng J等[6]提出一种BAN分类器，每个属性拥有不止1个非类别的父结点，完全放宽了属性间独立性的要求，属性间的相关性得以充分表达。爬山搜索算法(HCS)和超父结点算法(SP)是选择最优父结点的有效算法[7]。石洪波[8]建立了一个双层限定的贝叶斯分类模型表达属性间的相关性。Kononenko[9]提出一种Seminaive Bayesian classifier，通过属性分组将属性相关性较强的属性分在一组，同一分组内允许属性间存在相关性。李玉杰[10]提出可以运用贪婪选择算法选择属性的最佳分组，同一分组内允许属性间存在相关性。

本文在运用x2统计对属性相关性进行分析的基础上，将属性相关性较强的属性分在一组，各个属性分组之间相互独立。在每个属性分组中，在非类的父节点和子节点之间添加一条有向边来表示相关属性间的相关性，在属性分组内扩展朴素贝叶斯分类器。

1 朴素贝叶斯分类器NBC(Naive Bayes Classifiers)

朴素贝叶斯分类是通过计算条件概率实现分类预测，条件概率计算的理论依据是贝叶斯定理[11]，但它的前提条件是相互条件属性相对独立且对分类的影响相同。贝叶斯定理：

(1)

其中：P(H)是先验概率，P(X|H)是条件概率，P(H|X)是进行分类预测的后验概率。

朴素贝叶斯分类是根据贝叶斯定理，在计算条件后验概率的基础上，按照后验概率值的大小完成对训练数据集中的样本的分类预测。

令S={A1,A2,……An,C}是训练数据集，其中A1,A2,……An是属性变量，C={c1,c2,……cm}是类别变量，ai是属性Ai的取值，实例xi=(a1,a2,……an)属于类cj的概率，由贝叶斯定理可表示为：

(2)

其中：P(cj)是类cj的先验概率，P(cj|a1,a2,……,an)是后验概率。

朴素贝叶斯分类基于最大后验规则，测试集中的实例xi将被分配给后验概率值最大的那个类。

朴素贝叶斯分类的前提条件是属性间的独立性和属性对分类影响的一致性，这种限制在一定程度上降低了计算难度，但也影响了它的分类效果。

2 属性相关性度量方法

2.1 基于x2统计的属性相关性度量[12,13]

设属性A的值为ai(i=1,2,…,m)，属性B的值为bj(j=1,2,…,n)，属性A、B的频度计算如表1所示。

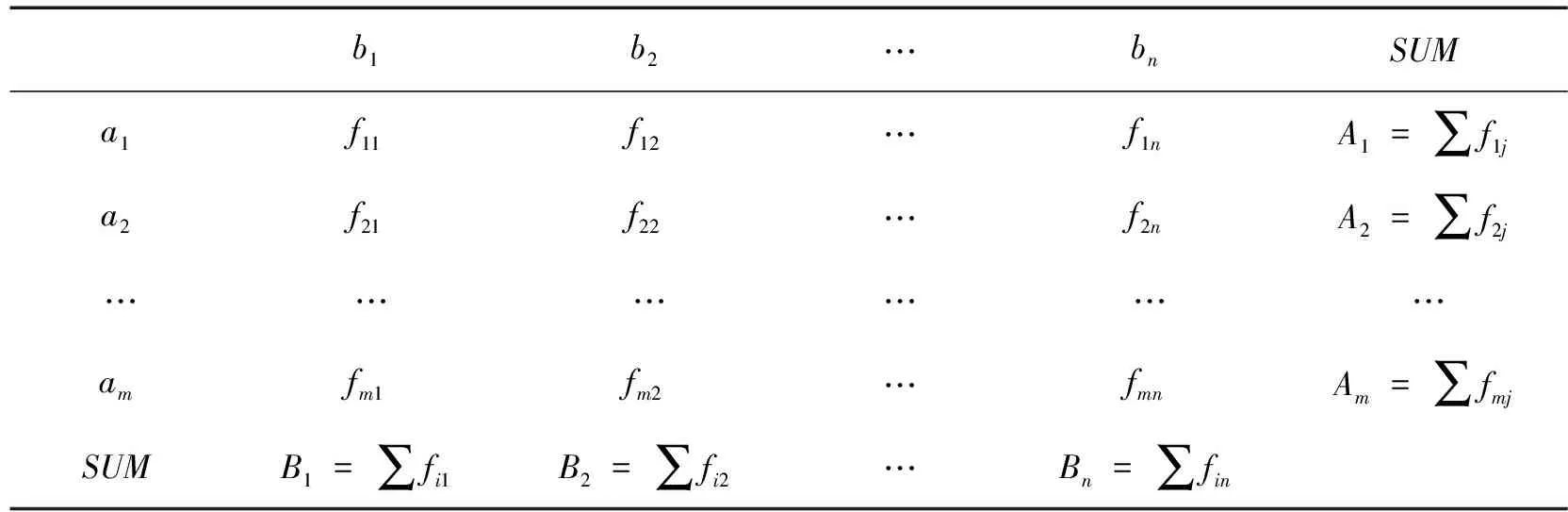
表1 属性的频度计算

x2统计的计算公式是：

(3)

公式中fij表示ai、bj同时出现的频度，Ai表示ai出现的频度，Bj表示bj出现的频度，f是数据集的样本数。属性相关性度量的公式为：

(4)

ψ是属性相关性的度量值，ψ的绝对值表示属性间的相关程度，该方法亦可作为属性与类别之间相关性的计算方法，用于表示属性对分类的影响程度。

2.2 属性分组算法

设变量集U={X1,X2,…Xn,C}，属性集X={X1,X2,……Xn}，目标属性分组π={π1,π2,…,πk}。首先，运用公式(3)和(4)，依次计算出每个属性与其它属性的ψ值；其次，计算每个属性ψ值的平均值，按照平均值的大小进行降序排列，属性分组中平均值最大的属性与其它属性相关性最强，可以作为每个属性分组的关键属性。算法流程描述如下：

(1)计算属性集中每个属性之间的属性相关性度量ψ(Xi,Xj)；

(2)计算每个属性与其它属性相关性度量值的平均值Eψ(Xi)；

(3)根据平均值Eψ(Xi)，将所有属性降序排列DescendSorted(Eψ(Xi))；

(4)将Eψ(Xi)最大值的属性作为第一个分组的关键属性，在所有ψ(Xi,Xj)中选择与Xi相关性最大的属性作为第一个属性分组中的属性，得到第一个属性分组π1；

(5)在剩余属性中选择平均值最大的Eψ(Xj)作为第二个分组的关键属性，在剩余属性所有ψ(Xi,Xj)中选择与Xj相关性最大的属性作为第二个属性分组中的属性，得到第二个属性分组π2；

(6)依次得到所有的属性分组πk。

3 基于属性分组的扩展朴素贝叶斯分类器KDANBC

3.1 基于属性分组的贝叶斯分类器的公式[10]

用πi作为变量集合X的一个属性分组划分，在分类时假设各个属性分组之间相互条件独立，组内各属性相互依赖，通过合理选取属性分组来达到改进分类器的目的，基于属性分组的贝叶斯分类器可以用公式表示为：

(5)

由上述模型可得出KDANBC模型如下：

(6)

通过上式，分母的值对于选定的数据集是一个定值，通常作为一个常数对待。因此，可以用下式来表示KDANBC的分类模型

(7)

πi表示属性集X的一个子集，对原数据集合X分组的合理性，将直接影响到分类的准确率，因此πi的合理选取与组合是分类器改进的关键。

3.2 基于属性分组的扩展朴素贝叶斯分类器KDANBC

朴素贝叶斯分类器改进方法可以通过在相关属性之间添加有向边的方式扩展朴素贝叶斯的结构，表达属性间的相关性。基于属性分组的扩展朴素贝叶斯分类器就是在每个属性分组中找到与其相关的属性，并限定属性分组内一个属性只拥有一个非类父结点，以简化扩展朴素贝叶斯的结构。算法流程描述如下：

(1)在第一个属性分组中选择绝对值最大ψ(π1i,π1j)；

(2)计算ψ(π1i,C)和ψ(π1j,C)，若ψ(π1i,C)>ψ(π1j,C),则π1i是π1j的非类父结点；若ψ(π1i,C)<ψ(π1j,C)，则π1j是π1i的非类父结点;

(3)在第一个属性分组剩余属性中选择绝对值最大ψ,按照步骤(2)依次为每个属性选择非类父结点：

(4)在第二个属性分组中，执行步骤(1)、步骤(2)、步骤(3)，为每个属性选择非类父结点；

(5)依次执行直到所有属性分组的每个属性都找到所对应的非类父结点；

(6)在各个属性分组中，在每对非类父节点和子节点之间添加一条有向边。

4 实验结果及分析

本文6个实验数据集均选自UCI数据集，数据集的基本情况如表2所示。首先，运用Weka[14]中的NBC和TAN算法测试每个数据集的分类正确率。其次，运用EDANBC算法进行测试，实验采取随机抽样，70%作为训练集，30%作为测试集，实验10次计算分类平均正确率，NBC、TAN和EDANBC分类正确率对比如表2所示。

表2 分类正确率对比表

本文采用分类正确率作为朴素贝叶斯分类性能的评价标准。如图1所示，与NBC对比，EDANBC的分类正确率在在每个数据集上均有一定程度的提高，分类性能明显改善；与TAN对比，EDANBC的分类正确率在4个数据集上比TAN的分类正确率高，在其他2个数据集Car Evaluation和Postoperative-patient上TAN的分类正确率要高一些。在实验的过程中发现，属性分组个数K的合理选取是分类器改进的关键，如果K的值过大，属性分组数过多，分类结构过于松散。一般情况下，如果属性变量个数不多于8个时，属性分2组是比较合理的选择。

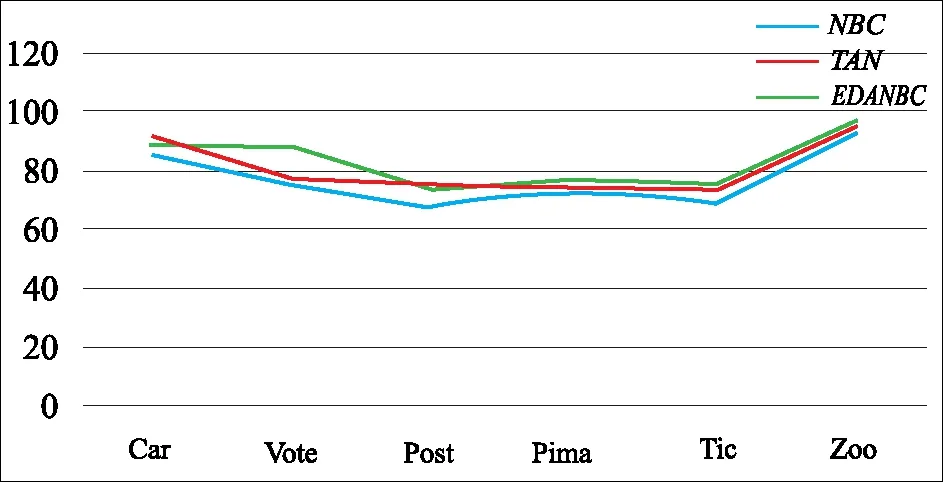
图1 分类正确率对比图

5 结 语

放松属性独立性假设和表达属性之间的相关性是提高朴素贝叶斯分类性能的主要方法之一，但构建朴素贝叶斯分类器计算的复杂度会随之增加。本文给出了基于x2统计的属性相关性度量及属性分组的方法，各个属性分组之间相互独立，组内各属性相互依赖。在每个属性分组中，在非类的父节点和子节点之间添加一条有向边来表示属性间的相关性，将朴素贝叶斯分类器的扩展限定在每个属性分组内，可以有效地简化扩展朴素贝叶斯分类器的结构，提高了分类的准确性。属性分组个数的合理选择与各个分组间的独立性的判定方法是分类器改进的关键，也是今后进一步关注和研究的方向。