超导电动磁悬浮列车次级悬挂半主动控制研究
2021-10-22张伟海曾靖淞闫兆盈马光同
张伟海,曾靖淞,闫兆盈,李 刚,马光同
(西南交通大学 牵引动力国家重点实验室,成都610031)
超导电动磁悬浮列车是目前唯一通过600公里速域等级应用可行性验证的轨道交通载运工具,有望成为下一代高速和超高速载人轨道交通的主要制式。由日本研发的L0 型超导电动磁悬浮列车于2015年实现了载人时速603公里运行[1-2]。动力学性能是超导电动磁悬浮列车进一步推向商业应用的主要挑战之一[3],超导电动磁悬浮列车作为载人公共交通工具在必须满足乘坐舒适性要求的同时也要尽可能地降低成本。车辆轻量化有降低生产成本、线路维护成本等优势。但是,车体轻量化会导致车辆隔振性能下降进而恶化车辆的动力学性能。在提高经济性的前提下改善超导电动磁悬浮列车的平稳性和舒适性,主要有提高线路等级和改进车辆悬挂系统两种途径。由于提高线路等级工程造价过高,因此,对超导电动磁悬浮车辆悬挂系统的设计和改进研究成为进一步改善车辆运行平稳性和舒适性的主要途径[4]。
为了提高和改善超导电动磁悬浮列车的动力学性能,Nagai等[5]建立了2自由度的车辆垂向模型,在次级悬挂中应用LQR主动控制方法,以车体和转向架的动能和势能构成二次型目标函数,从仿真和实验两方面初步验证了LQR 主动控制方法可以减少车体振动传递效率以及降低车体振幅。Watanabe等[6]建立了3 辆车体和2 台转向架铰接式组成的10自由度超导电动磁悬浮列车的垂向-俯仰动力学模型,在中间车体的次级悬挂中应用了基于LQ理论的主动控制方法,验证了LQ控制方法抑制车体垂向振动的有效性。Hoshino K 等[7]建立了3 辆车体和4 台转向架铰接式组成的14 自由度超导电动磁悬浮列车垂向-俯仰动力学模型,在中间车体的次级悬挂中应用了LQG主动控制方法,仿真验证了该控制方法可以降低中间车体垂向振动幅值。
在超导电动磁悬浮列车动力学性能的研究中,大多数学者仅考虑了编组车辆中间车体垂向运动的振动控制,没有考虑中间车体俯仰运动以及头车或尾车的振动控制。此外,在之前的工作中大多采用主动控制这种需要耗费大量能量的控制方法。
基于此,本文在建立14自由度超导电动磁悬浮列车垂向-俯仰动力学模型的基础上,分析车体垂向速度与垂向加速度的耦合作用关系,提出一种耗能较少的改进天棚阻尼半主动控制方法,在3 辆编组车体的次级悬挂中应用改进天棚阻尼半主动控制方法来探究不同车体的垂向和俯仰运动的动力学性能。以被动控制和应用广泛的天棚阻尼半主动控制方法作为参照对象,验证了所提出的改进天棚阻尼半主动控制方法可以有效提高超导电动磁悬浮车辆的乘坐舒适性。
1 车辆动力学模型
图1 为超导电动磁悬浮列车与轨道的结构简图。超导电动磁悬浮列车系统主要由车体、安装有超导磁体的转向架以及安装“8”字形悬浮线圈和推进线圈的U型轨道组成。在推进线圈中通入三相交流电后,将在U 型轨道中产生沿着车辆前进方向的行波磁场。车辆经过时车载超导磁体产生的磁场与轨道上的行波磁场及“8”字形悬浮线圈相互作用从而产生推进力、悬浮力和导向力,当车辆运行速度超过100 km/h时,悬浮力平衡车辆重力使车体悬浮[8]。

图1 超导电动磁悬浮车辆结构
为了研究编组列车中车辆的垂向动力学性能以及车辆的振动控制,本文建立了由3辆车体和4台转向架铰接式组成的超导电动磁悬浮列车动力学模型,如图2 所示。模型考虑了车辆和转向架垂向与俯仰两个方向上共14个自由度。为了简化计算,其中车体和转向架均视为刚体,在计算中不考虑其弹性变形。在初级悬挂中,用两个线性磁弹簧等效代替车辆转向架与地面轨道“8”字形线圈之间的垂向力和俯仰力矩,一个磁弹簧位于转向架的前部,另一个位于转向架的后部,用该等效处理方法可以解耦垂向和俯仰方向的耦合力[3,6-7]。由于车辆在高速运行过程中,轨道与转向架之间的阻尼系数接近于零,因此将其忽略不计[9]。车辆的次级悬挂主要由空气弹簧和被动阻尼器组成。由于空气弹簧的刚度和被动阻尼器的阻尼系数不能根据车辆振动状态进行实时调节以适应车辆的最佳运行状态,称这种模型为被动控制模型。本文将主要研究在次级悬挂中分别采用天棚阻尼控制和改进天棚阻尼半主动控制方法对编组车辆的振动控制效果,以实现提高车辆乘坐舒适性的目标。

图2 车辆动力学计算模型
基于牛顿-欧拉方程,推导出车辆被动控制模型的动力学方程,其矩阵形式如式(1)所示,一般形式的动力学方程参见附录。式(1)中,M14×14表示车辆质量矩阵,C14×14表示阻尼矩阵,K14×14表示刚度矩阵,X14×1表示位移向量,P(t)表示轨道激励。表1列出了动力学方程中的主要参数[10]。

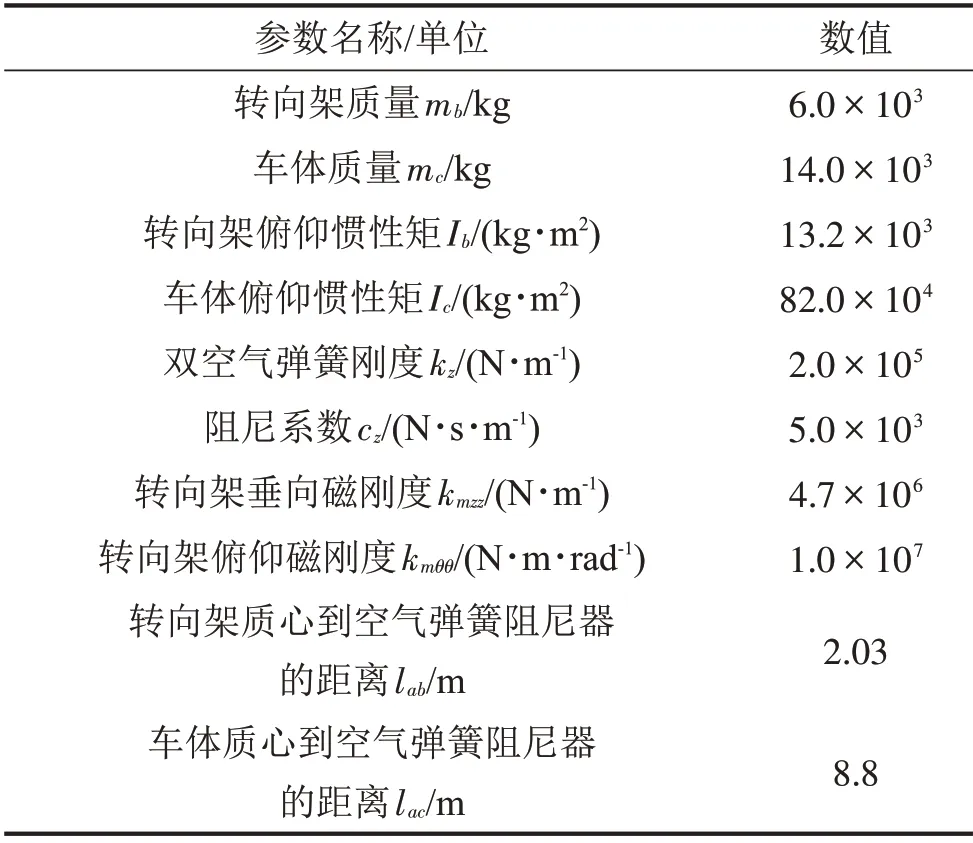
表1 超导电动磁悬浮列车主要参数
2 轨道不平顺
轨道不平顺是轮轨车辆、电磁悬浮车辆、超导电动磁悬浮车辆等轨道交通载运工具与轨道线路系统产生随机振动的主要根源,直接影响着车辆的运行平稳性与乘坐舒适性。超导电动磁悬浮列车U型轨道上“8”字形线圈垂向排列不平整是引起车辆垂向振动的主要因素[11]。
2.1 时间域轨道不平顺谱密度函数
本文通过逆傅里叶变换法,首先将轨道不平顺空间功率谱密度函数变换为时间域上的轨道不平顺功率谱密度函数,然后将时间域上的轨道不平顺功率谱密度函数转换为轨道不平顺时间序列样本,为超导电动磁悬浮车辆振动控制研究提供时域输入[12]。
本文利用如式(2)[10]所示的超导电动磁悬浮车辆空间域轨道不平顺功率谱密度拟合公式来反演生成轨道不平顺时域序列。
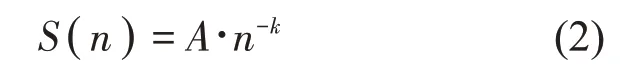
式中:S(n)为空间域中轨道不平顺功率谱函数,单位是(mm2)m;A为轨道粗糙度常数;n表示空间域频率,为空间波长的倒数,单位是1/m,k为波数。本文取A=0.02,k=1.8。
利用轨道谱曲线在微小频带的面积相等原理[13-14],可得:

当车辆以速度v运行时,通过空间频率为n的空间波时将产生频率为Δf的一个激励,即:

式中:f为时间域频率,单位为Hz。
设σ2为功率谱密度在空间域频带宽度Δn和时间域频带宽度Δf包含的功率,则这两种功率谱密度分布函数分别为:
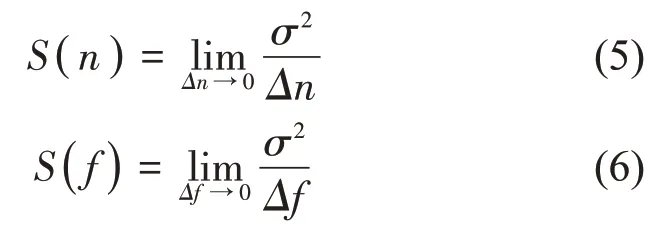
由式(2)至式(6)可得时间域功率谱密度函数为:
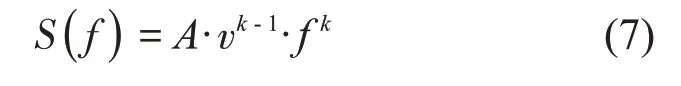
2.2 逆傅里叶变换法生成轨道不平顺时间序列
本文计算中设定车辆运行速度为500 km/h,轨道不平顺波长范围为3.216 m~398.107 m。根据式(7),基于逆傅里叶变换通过MATLAB编程得到在时间域上的轨道不平顺时间序列,计算结果如图3所示。
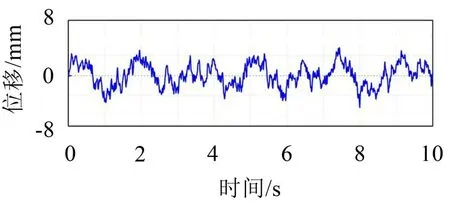
图3 轨道垂向随机不平顺时间序列
现验证基于逆傅里叶变换得到的轨道不平顺时间序列的正确性。对图3所示的轨道不平顺时间序列求其功率谱密度得到模拟值,然后与式(7)得到的功率谱密度解析值相比较,结果如图4 所示。两者吻合程度较好,故验证了本文通过数值模拟方法得到的超导电动磁悬浮轨道不平顺时间序列的可靠性。
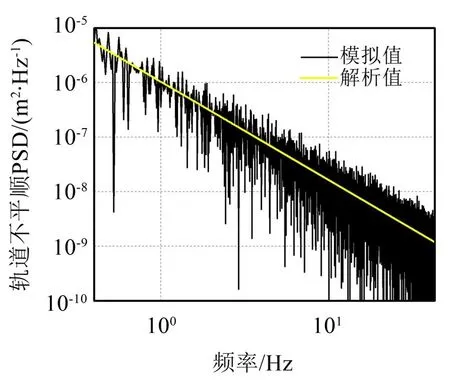
图4 轨道垂向随机不平顺PSD
3 次级悬挂半主动控制方法
3.1 被动控制模型验证
图5是在MATLAB/Simulink环境中搭建的被动控制模型。为了验证所搭建模型的正确性,本文基于新型快速显式积分法[15]编程求解了车辆被动控制模型的动力学方程。在轨道不平顺时间序列的激励下,上述两种数值计算方法求解车辆动力学方程的位移响应如图6所示。这两种求解方法计算所得的位移响应高度吻合,故验证了本文所搭建的被动控制模型的正确性。
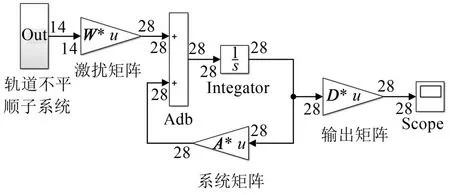
图5 超导电动磁悬浮列车被动控制模型
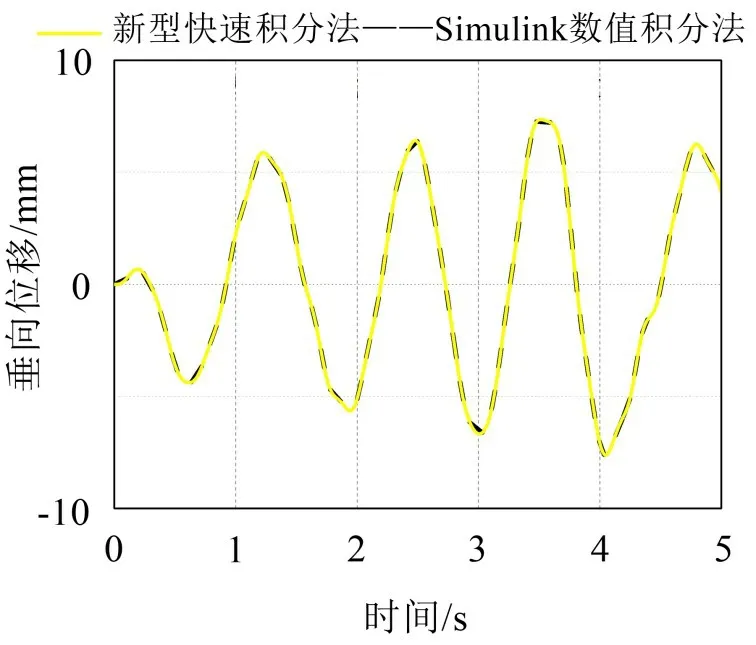
图6 超导电动磁悬浮车体位移响应
3.2 天棚阻尼控制算法
天棚阻尼原理如图7所示。假想在车体和固定的“天棚”之间安装阻尼为Cs的虚拟惯性阻尼器,通过控制减振器的阻尼,使减振器阻尼力尽量接近天棚阻尼器的阻尼力。由于在实际中无法实施这样理想的控制力,因而在车体mc和转向架mb之间安装一个作动器Uz产生作用于车体和转向架的可变阻尼力。
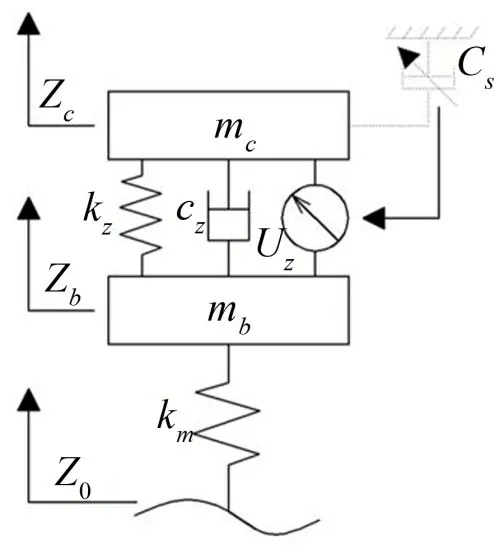
图7 天棚阻尼控制原理示意图
在天棚阻尼控制中一般通过“ON-OFF”型控制律调节阻尼系数来实现瞬时阻尼力的变化。当车体垂向速度与车体相对于转向架的相对速度方向相同时,阻尼器对车体做负功,作动器Uz提供设定的最大阻尼力来加速抑制车体的振动;当车体垂向速度与车体相对于转向架的相对速度方向相反时,阻尼器对车体做正功,为了避免转向架振动传递给车体,此时作动器产生的阻尼力取最小值。
在车辆被动控制模型的次级悬挂中并联8个天棚阻尼器,如图2所示,即分别在每个转向架与车体之间都安装一个作动器Uzi(i=1,2,…,8)来抑制车体的振动,作动器提供的阻尼力由式(8)表示。

本文采用的“ON-OFF”型控制律的天棚阻尼半主动控制算法的表达式如式(9)所示。
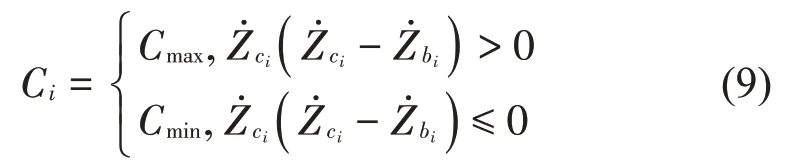
3.3 改进天棚阻尼控制算法
由式(9)可知,天棚阻尼控制方法实质上是通过控制车体的垂向速度来抑制车体振动的,没有考虑车体垂向速度和垂向加速度的相互作用关系,所以天棚阻尼控制方法对车体的控制效果是有限的。又因为车辆的垂向平稳性一般通过车体的垂向加速度来评价,因此,基于天棚阻尼控制方法,引入车体的垂向加速度,形成了改进天棚阻尼控制方法,即通过判断车体垂向速度和垂向加速度的相互关系来控制车体加速度,其控制算法的表达如式(10)所示。
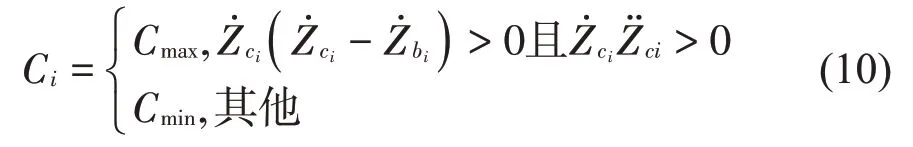
4 控制方法性能分析
为了分析改进天棚阻尼半主动控制方法的有效性,以被动模型和天棚阻尼半主动控制模型作为参照,分别以头车Car1和中间车Car2质心处的垂向加速度、俯仰加速度作为评价指标进行时域和频域分析。
在MATLAB/Simulink 环境中分别搭建超导电动磁悬浮车辆的被动模型、天棚阻尼和改进天棚阻尼半主动控制模型。模型结构参数如表1所示。主要仿真参数如下:Cmax=7 kN·s/m,Cmin=0,仿真步长为10-4s,仿真时间为30 s。
4.1 时域分析
图8 至图10 是在上述控制条件下,Car1 和Car2质心处的垂向加速度、俯仰加速度以及阻尼器作用于Car2 的控制力的计算结果。为了使仿真结果显示更清晰,下面时域结果均显示前10 s的计算结果。表2 是在0~30 s 时间段内各指标的均方根值和峰值的绝对值。
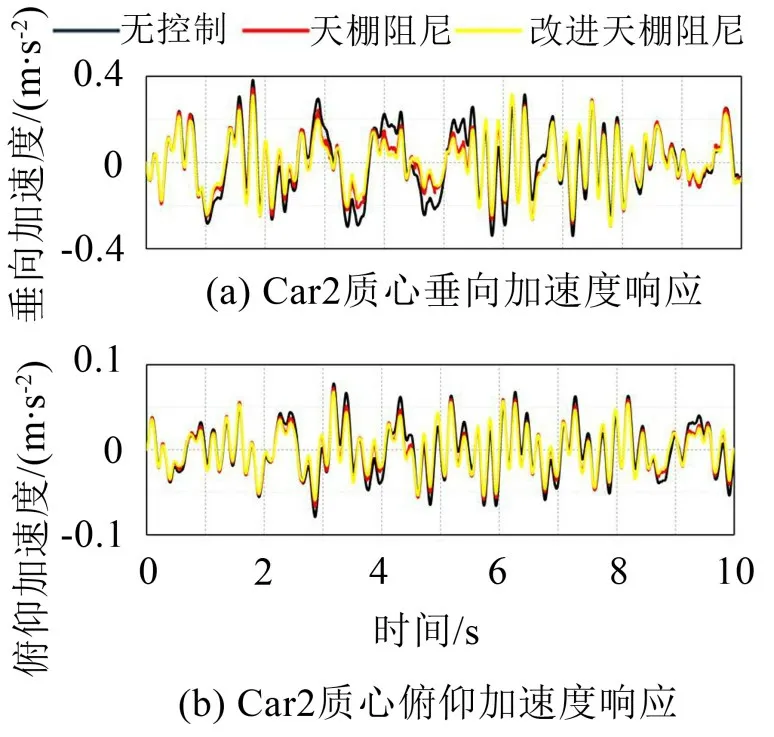
图8 Car2加速度时域响应
由图8可知,在改进天棚阻尼控制方法作用下,中间车体Car2 的垂向加速度和俯仰加速度的峰值明显被抑制。相比被动控制,Car2 质心处的垂向加速度在改进天棚阻尼半主动控制方法下的均方根值和峰值分别降低了19.77%和6.31%,在天棚阻尼半主动控制方法下的均方根值和峰值分别降低了14.72%和4.55%。
相比被动控制,在改进天棚阻尼半主动控制方法下Car2 质心处俯仰加速度的均方根值和峰值分别降低了17.34%和13.76%,在天棚阻尼半主动控制方法下的均方根值和峰值分别降低了12.15%和8.29%。综上,对于中间车体Car2的振动控制,改进天棚阻尼控制方法的减振效果要优于天棚阻尼方法。
接着对比这两种半主动控制方法对编组车体中头车Car1 或尾车Car3 振动抑制效果。在超导电动磁悬浮编组车辆模型中,因为头车与尾车结构对称,所以只需分析其中之一即可,本文选择头车Car1作为研究对象。由图9 可得,改进天棚阻尼控制方法对Car1 垂向和俯仰两个方向上振动抑制效果要略好于天棚阻尼控制,具体计算结果如表2 所示。同时,可以看到,改进天棚阻尼控制方法对Car1 振动控制的效果不及Car2。计算Car1 车体前端与两个作动器连接点中点处的加速度均方根值为0.392 m/s2,Car1 车体后端与作动器连接点的加速度均方根值为0.238 m/s2,说明Car1 后端的平稳性要优于Car1前端,所以改进天棚阻尼控制方法对Car1振动控制的效果不及Car2 的原因可能是编组车辆中铰接式转向架结构导致了Car1 前后二系悬挂的结构不对称,在一定程度上恶化了车体Car1 的乘坐舒适性。
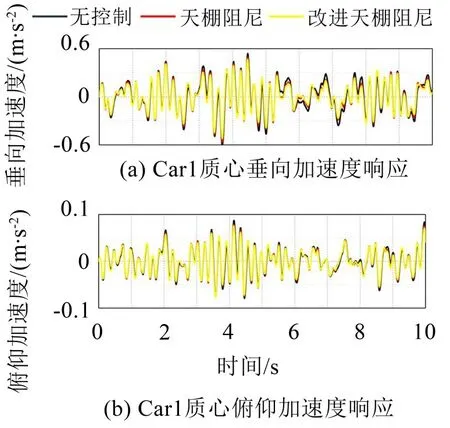
图9 Car1加速度时域响应
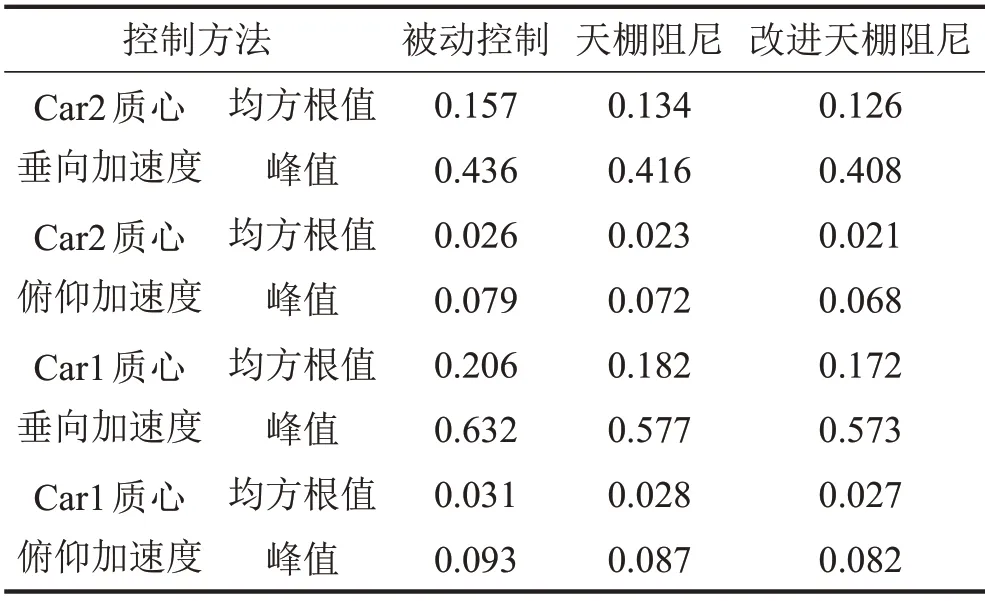
表2 评价指标均方根和峰值计算结果/(m·s-2)
最后对比这两种半主动控制方法的控制效率。由图10可知,作动器在改进天棚阻尼控制方法下输出的控制力具有比较小的振幅。对于车体Car2 的垂向控制力,改进天棚阻尼控制方法作用下的控制力在0.517 kN 之内,而在天棚阻尼控制方法作用下的控制力可达0.593 kN,改进天棚阻尼控制的控制力减小了12.8%。因此,在达到相同控制效果的情况下,改进天棚阻尼半主动控制方法的效率更高,在实际应用中可以允许设计更小的作动器和更小的最大控制力。对于车体Car2 在俯仰运动方向上控制力的时域响应分析,也能得到同样的结果。
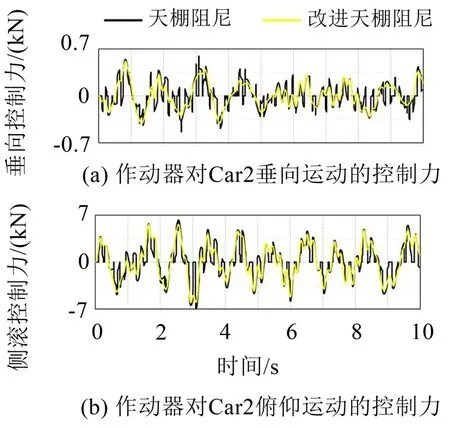
图10 控制力时域响应
4.2 频域分析
图11 是对中间车体Car2 质心处的垂向加速度和俯仰加速度功率谱分析得到对应的功率谱密度曲线。从图11 中可知存在两个明显的加速度PSD 峰值,一个峰值位于1 Hz附近,是车体的主频振动;另一个峰值位于5 Hz附近,是转向架的主频振动。从图11可知,车体主频振动峰值在改进天棚阻尼半主动控制方法的作用效果也要优于天棚阻尼半主动控制方法的作用效果。
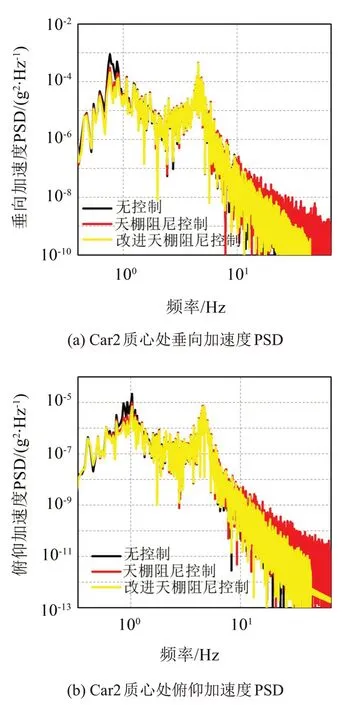
图11 Car2加速度频域分析
相比被动控制下Car2 质心处的垂向加速度PSD 在1 Hz 附近的峰值,在改进天棚阻尼半主动控制下1 Hz附近的峰值降低了约4.27倍;在天棚阻尼半主动控制方法下1 Hz 附近的峰值降低了约2.9倍。相比被动控制下Car2 质心处的俯仰加速度PSD 在1 Hz 附近的峰值,在改进天棚阻尼半主动控制下1 Hz 附近的峰值降低了约3.1 倍;在天棚阻尼半主动控制方法下1 Hz附近的峰值降低了约2.3倍。但是,由于次级悬挂中阻尼力仅对车体有减振作用,且本文研究中没有对初级悬挂进行控制,因此,约5 Hz的转向架主频振动峰值没有明显变化。
5 结语
本文以改善车辆乘坐舒适性为目标,建立了3辆车体与4台转向架铰接式组成的14自由度超导电动磁悬浮编组列车的垂向-俯仰动力学模型,在轨道垂向随机不平顺的激励下,从时域和频域两个方面,探究了天棚阻尼和改进天棚阻尼两种半主动控制方法应用于超导电动磁悬浮列车次级悬挂中对车体振动的影响,可得到以下结论:
(1)相比被动控制,在天棚阻尼半主动控制方法作用下Car2 质心处的垂向加速度和俯仰加速度的均方根值分别降低了19.77%和17.34%;在改进天棚阻尼半主动控制方法作用下Car2 质心处的垂向加速度和俯仰加速度的均方根值分别降低了14.72%和12.15%;获得相同减振效果的条件下,改进天棚阻尼控制相较于天棚阻尼控制方法控制力减小了12.8%。从控制效果和控制效率两个角度看,改进天棚阻尼半主动控制方法要优于天棚阻尼半主动控制方法。
(2)在编组车辆的车体振动控制中,改进天棚阻尼半主动控制方法对中间车体Car2 的控制效果要优于头车车体Car1,其原因可能是编组车辆中铰接式转向架结构导致了Car1 前后二系悬挂的结构不对称,在一定程度上恶化了车体Car1 的乘坐舒适性。
(3)在超导电动磁悬浮次级悬挂中应用半主动控制方法,仅能够有效抑制车体的低频振动,其高频振动依然显著,车体的高频振动要通过初级悬挂减振方法来抑制。
附录:
该附录是基于牛顿-欧拉方程,得到的车辆被动控制模型一般形式的动力学方程,如式(1)至式(14)所示。其中,下标b和c分别表示转向架和车体,zbi和θbi(i=1,2,3,4)分别为转向架的垂向位移和俯仰角位移;zcj和θcj(j=1,2,3)分别为车体的垂向位移和俯仰角位移;z0if和z01r(i=1,2,3,4)为轨道不平顺激扰。
转向架1的垂向运动:

转向架1的俯仰运动:

转向架2的垂向运动:

转向架2的俯仰运动:
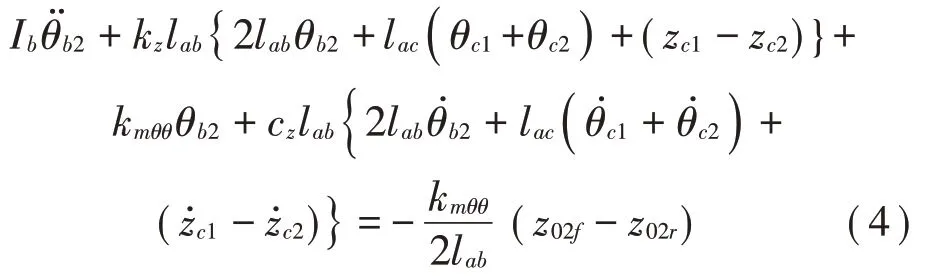
转向架3的垂向运动:

转向架3的俯仰运动:

转向架4的垂向运动:

转向架4的俯仰运动:
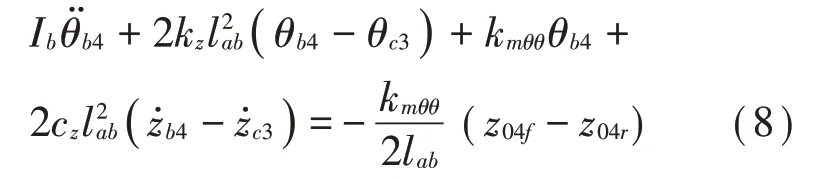
车体1的垂向运动:

车体1的俯仰运动:
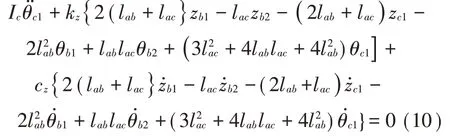
车体2的垂向运动:
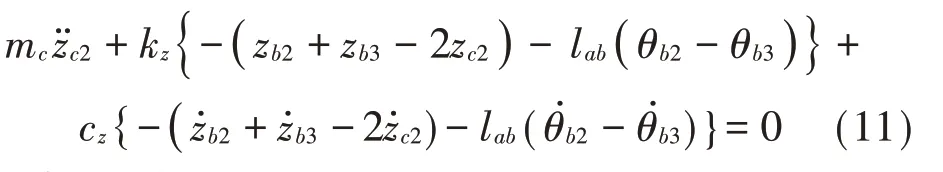
车体2的俯仰运动:

车体3的垂向运动:

车体3的俯仰运动:

