非线性系统载荷识别的最小二乘支持向量机法
2021-10-22辛江慧丁继才
周 盼,辛江慧,丁继才
(1.南京工程学院 汽车与轨道交通学院, 南京211167;2.海军装备部驻葫芦岛地区军事代表室, 辽宁 葫芦岛125004)
载荷识别,即采用结构的振动响应,结合结构振动特性求解作用于结构的外部激励(或载荷)。载荷识别对于结构振动预测、优化设计、故障诊断均具有重要意义。近些年来,载荷识别问题的研究比较深入,不少学者对该问题的研究进展进行了总结归纳[1-3]。
逆系统法,作为一种解决逆问题的有效方法,应用广泛。1995年,魏星原等[4]通过建立自回归滑动平均逆系统,进而求解激励。然而只有当线性系统满足可逆、稳定、能控、能观时其逆系统才存在。1999年,Steltzner[5]提出采用非因果逆向结构滤波器识别结构所受激励。受测试噪声的影响,系统矩阵的奇异性导致载荷识别结果不稳定。为改善该问题,2008年,Allen等[6]提出一种延迟逆向滤波器算法计算系统的外部激励。随后,周盼等[7-8]提出采用自适应滤波器模拟逆系统,并引入延迟环节以提高逆系统建模精度,进而识别单点、多点激励的时间历程。
随着计算机技术的发展,新兴的控制算法不断引入载荷识别中。1998年,Ma等[9]以线性集中质量系统为研究对象,采用卡尔曼滤波器和递归最小二乘(Recursive least square,RLS)法识别冲击载荷。然而实际工程结构中存在非线性因素这一客观事实,使得很多学者对非线性系统的载荷识别问题日益关注。2004年,Ma等[10]采用广义卡尔曼滤波器和RLS 将载荷识别拓展到了非线性系统上。其后,Lin[11]采用同样方法对单自由度非线性系统进行外载荷的数值仿真研究。宋雪刚等[12]采用容积卡尔曼滤波器对非线性梁系统进行载荷识别的理论和实验研究。然而这些方法均是建立在系统的状态空间模型基础上的,要求清晰地了解系统的数学模型,限制了其在实际工程中的应用和推广。
由于支持向量机(Support vector machine,SVM)方法具有小样本学习能力强、模型泛化性能好、能处理高维数据等优点,被引入到载荷识别问题中。郝云霄等[13]建立了基于SVM 的飞机机翼载荷模型,验证了SVM 的有效性。2013年,曹善成等[14]提出了一种改进的SVM回归飞行载荷识别模型,利用飞行参数识别半滚机动动作下某一部位弯矩。
由于SVM采用二次规划方法求解问题,存在训练时间较长、计算较复杂等缺点。基于此,LS-SVM应运而生。Hu等[15]和Mao等[16]采用LS-SVM对频域载荷进行重构。基于前人的研究,本文拟采用LSSVM识别非线性系统的时域载荷。
1 最小二乘支持向量机
1999年,Suykens 提出LS-SVM,采用最小二乘线性系统作为损失函数,代替SVM采用的二次规划算法,运算简单,收敛快,精度高[17]。
下面介绍LS-SVM 的辨识原理[18]。L组训练样本集(xl,yl),l=1,2,…,L,输入xl∈ℝn输出yl∈ℝ。非线性函数估计为:
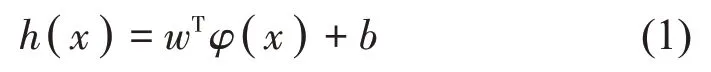
其中权向量w∈ℝn偏置值b∈ℝ,非线性映射φ(·)把样本从原空间映射到高维特征空间。函数估计问题可描述为下列形式:

其中:γ为惩罚因子(正则化参数),el为不敏感损失函数的松弛因子。采用拉格朗日法求解该优化问题:

式中:αl为拉格朗日乘子。根据Karush-Kuhn-Tucher(KKT)最优化条件,可得:
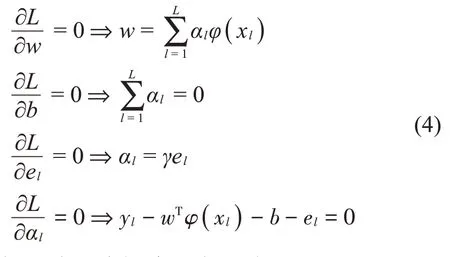
将式(4)表示为矩阵形式,可得:
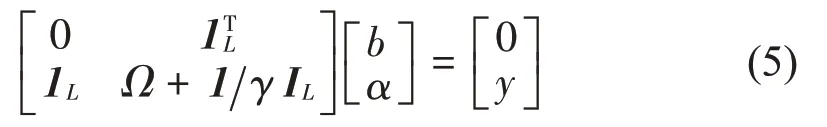
式中:α=[α1,α2,…,αL]T,y=[y1,y2,…,yL]T,IL为单位阵。1L=[ 1,1,…,1]T。
Ωij=K(xi,xj)=φ(xi)Tφ(xj)是满足Mercer 条件的核函数。目前常用核函数的有线性、多项式和高斯核函数。高斯核函数(或径向基核函数)是具有全局收敛特性的线性学习算法前馈网络,其学习速度快,应用广泛。在此选用高斯核函数,表示形式如下:

其中:σ为核宽度。
通过L组训练样本集(xl,yl)计算出输入向量系数α1,α2,…,αL和阈值b。此时,最小二乘支持向量机回归估计为:
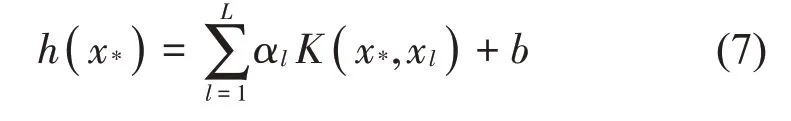
2 非线性连续系统的逆模型辨识
SISO 非线性连续系统的振动微分方程可表示为如下简易形式:

对上述SISO非线性连续系统,若在某开集D内有∂f/∂u≠0,且在D内处处连续,则该系统可逆[19]。当上述非线性系统存在逆系统时,逆系统可表示为:

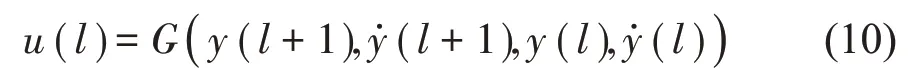
逆模型辨识的训练样本的输入数据为x(l)=输出数据为相应的激励u(l)。根据式(10)可知,采用该时刻及下一时刻的速度、位移拟合该时刻的激励。通过LS-SVM 的学习,由式(5)计算出输入向量系数α1,α2,…,αL和阈值b,从而将输入空间的数据利用非线性映射函数φ(·)投影到特征空间进行线性拟合。
3 基于LS-SVM算法的载荷识别
基于LS-SVM 的载荷识别流程如图1 所示。首先获得非线性系统在白噪声激励下的振动响应,以其作为训练数据对非线性系统进行逆模型辨识。以训练数据中的振动响应作为非线性系统的输入数据,白噪声激励作为输出数据,通过选取合适的LSSVM算法参数,利用LS-SVM算法即可获得非线性系统的逆模型。然后以非线性系统实际工作状态下的响应为逆模型输入,则逆模型输出即为待识别的激励。该方法不需要获得系统的状态空间模型,即不再依赖于系统的具体数学模型和系统参数,少量的输入输出样本数据即可完成逆模型辨识过程,为载荷识别作好准备工作。
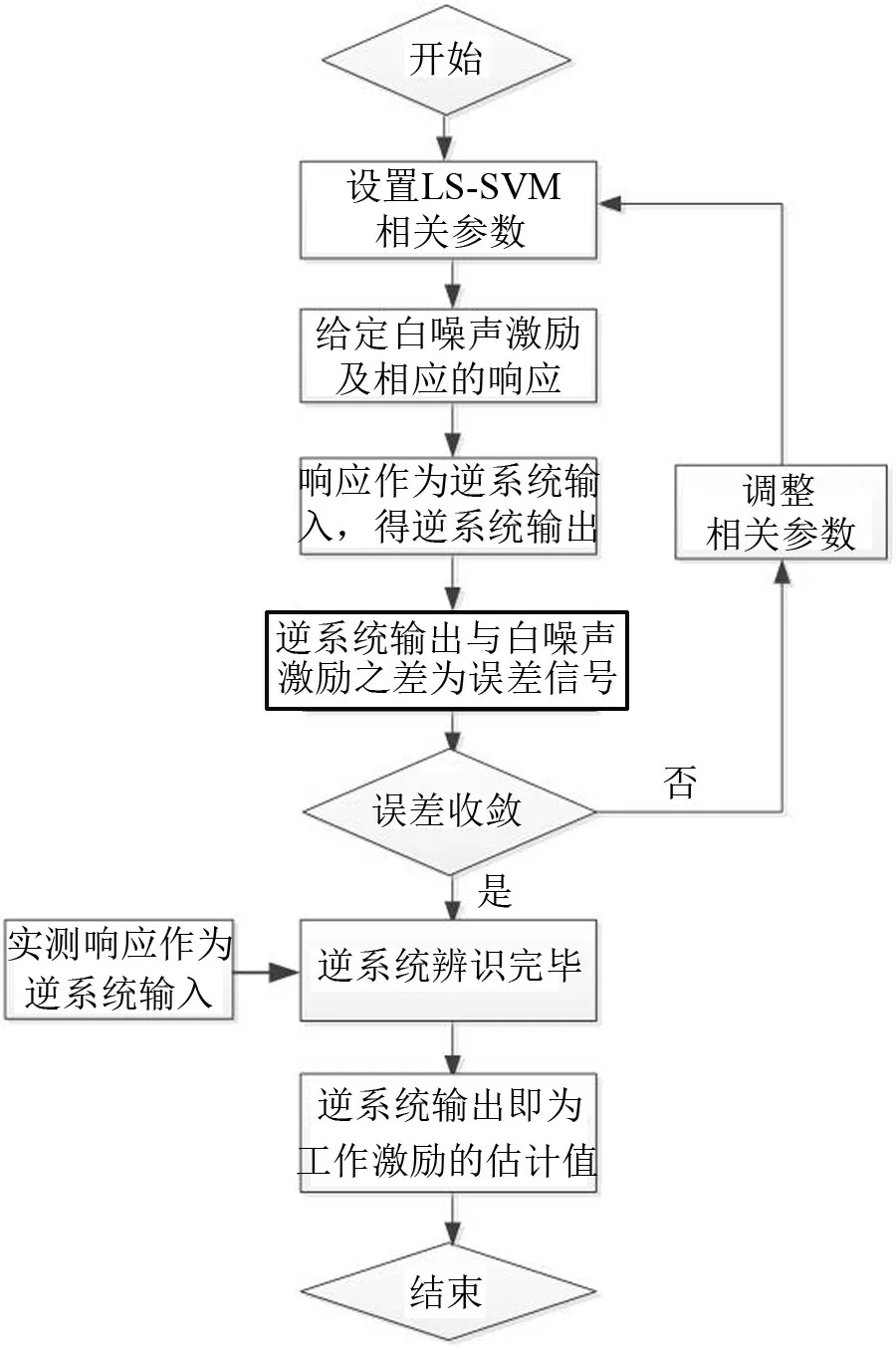
图1 基于LS-SVM算法的载荷识别流程图
4 仿真结果与分析
4.1 非线性系统的逆模型辨识
本文参考文献[20]中采用的非线性系统,在此以Duffing 非线性振子为研究对象,Duffing 振动方程为:

其中:m=1kg,c=0.4 N·s/m,k1=1.1N/m,k2=1N/m。初始位移和速度分别为=0 ms-1。
逆系统辨识过程应选取足够丰富的激励信号,以期充分反映出逆系统的动态特性。在此选用均值为0,方差为1 的随机激励信号及相应的速度、位移响应作为逆模型辨识的训练样本。采样时间分辨率为0.1 s,采样时间为20 s。随机激励的时间历程如图2 示。采用经典Runge-Kutta 法计算非线性系统在随机激励下的速度、位移响应,如图3所示。

图2 随机激励的时间历程

图3 随机激励作用下系统的速度、位移响应
以上述速度响应和位移响应作为训练样本的输入数据,随机激励作为输出数据,对非线性系统进行逆模型辨识。LS-SVM的参数选取为:惩罚因子γ=1.5×1010,径向基核宽度σ=10。
逆模型辨识结果如图4所示。仿真结果显示估计激励与真实激励吻合很好,说明非线性系统的逆模型辨识准确。值得一提的是图中20 s时的激励未进行识别,给定值为0,这是由于在逆模型辨识过程中采用的是该时刻及下一时刻的速度和响应识别该时刻的激励造成的。

图4 逆模型输出与随机激励对比
4.2 稳态激励识别结果
非线性系统的逆模型辨识完成后,获得输入向量系数和阈值。在此基础上,对非线性系统分别施加稳态和非稳态激励,利用Runge-Kutta法获得相应激励下的速度和位移响应,以此作为逆模型的输入数据,则逆模型的输出即为外部激励的估计值。
首先,考察对非线性系统施加如下稳态正弦激励:
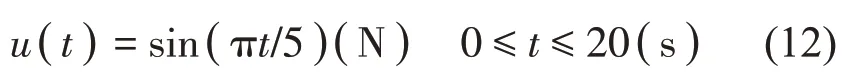
时间分辨率为0.1 s。在此正弦激励作用下,非线性系统的速度、位移响应如图5 所示。正弦激励识别结果见图6,仿真结果显示识别的正弦激励与实际激励吻合得很好。
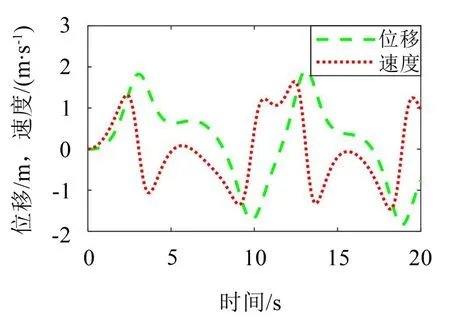
图5 正弦激励作用下系统的速度、位移响应

图6 识别激励与实际激励的对比图
对非线性系统施加如下双频正弦激励:

采用Runge-Kutta 法计算得到的非线性系统的速度、位移响应如图7 所示。基于非线性系统的逆模型获得激励的估计值,如图8所示,结果表明识别激励与真实激励吻合得很好。

图7 双频正弦激励作用下系统的速度、位移响应

图8 识别激励与实际激励的对比图
通过对正弦激励、双频正弦激励的识别计算,结果表明基于LS-SVM逆模型的识别方法能够比较精确地反演出非线性系统的稳态激励。
4.3 非稳态激励识别结果
下面对非线性系统的非稳态激励进行识别研究。对非线性系统施加半正弦冲击激励,表达式如下示:
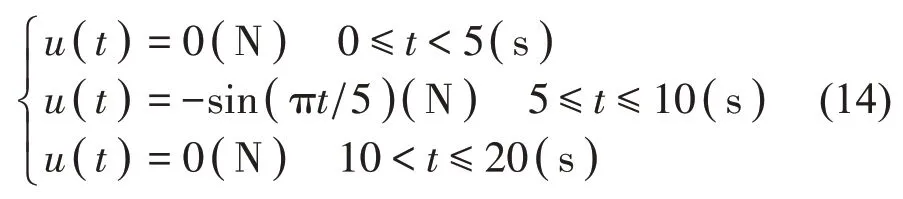
该冲击激励下非线性系统的速度、位移响应见图9,识别的激励结果如图10 所示。仿真结果显示冲击激励识别结果精度也较高,与实际冲击激励几乎吻合。

图9 半正弦冲击激励作用下系统的速度、位移响应
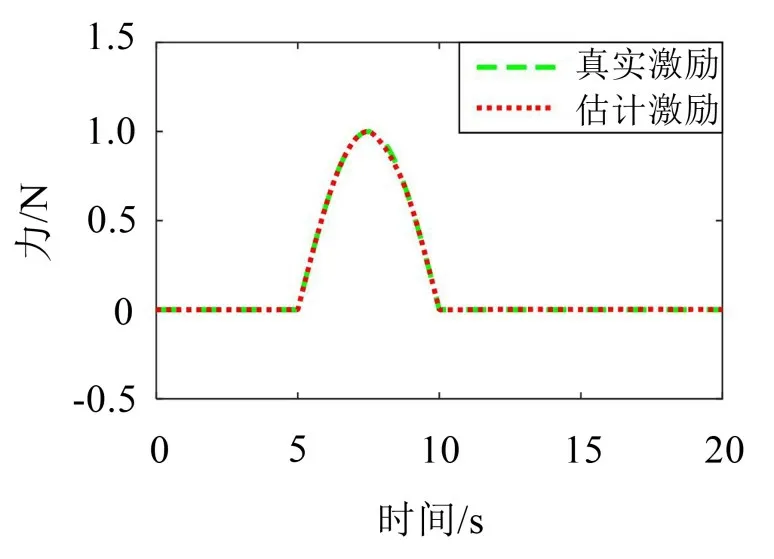
图10 识别激励与实际激励的对比示意图
最后,对作用于非线性系统的随机激励进行仿真计算。随机激励下系统的速度、位移响应如图11所示,随机激励的识别结果如图12 所示。同样,随机激励的识别结果也令人满意。这说明基于LSSVM算法的逆系统方法,不仅能准确识别时域稳态激励,对非稳态激励也是适用的。

图11 随机激励作用下系统的速度、位移响应

图12 识别激励与实际激励的对比示意图
需要注意的是,在上述列举的4 种不同形式的时域激励识别过程中,20 s 时刻的激励均未予以识别,而是设定为0,这是由于非线性系统的逆模型辨识造成的。原因之前已经叙述,不再赘述。
5 结语
本文将LS-SVM回归算法引入到非线性系统的时域载荷识别问题中,获得了较满意的识别结果。采用LS-SVM 算法进行非线性系统的逆模型辨识,在此逆模型基础上,采用工作速度响应和位移响应识别时域工作载荷。将载荷识别的这个复杂的逆问题转化为最优化问题和正问题进行处理。仿真结果表明:该方法选取适当的LS-SVM参数,就能够保证逆模型的学习能力和泛化能力;采用LS-SVM 方法能有效地反演非线性系统的稳态、非稳态载荷。此外,该方法不需要系统模型的先验知识,只要知道少量的输入输出样本即速度、位移响应和激励即可建立非线性系统的逆模型,能够推广到实际工程应用中。
本文提出的基于LS-SVM算法的时域载荷识别方法为载荷识别技术提供了一条新的思路和途径,具有一定的使用价值。本文中只对非线性系统的单激励情况进行了研究,对采用LS-SVM 算法识别多激励源的情况,理论上是可行的,需要深入研究。
