基于谱归纳的车辆振动分析
2021-10-22韩兴晋周劲松邓辰鑫
韩兴晋,周劲松,邓辰鑫
(同济大学 铁道与城市轨道交通研究院,上海201804)
目前,我国轨道交通车辆向着高速、高频、重载等方向不断发展,导致车辆振动问题越发严重,运行平稳性和乘坐舒适度降低,甚至会导致车辆部件脱落和疲劳失效。为检验车辆在振动环境中的安全可靠性,对振动数据进行恰当的归纳处理非常重要。目前振动数据归纳在我国航空领域应用较为广泛[1-2],并制定了随机振动数据归纳方法军用标准GJB/Z126-1999[3],按照一定置信度和数据分位点归纳振动数据的容差上限。厉鑫波等[4-5]应用GJB/Z126-1999 数据归纳方法对实测振动数据进行归纳,对车辆设备进行了疲劳分析。然而在轨道车辆运行时实测振动数据更多呈现非正态分布特征,Slifker等[6]提出约翰逊法则,利用正态拟合函数对非正态情形的随机振动数据进行拟合。罗敏等[7]应用约翰逊法则拟合非正态振动数据,解决了飞行器运行时振动数据非正态问题。邓辰鑫等[8-9]提出应用约翰逊法则对GJB/Z126-1999 数据归纳方法进行优化的思想,应用于轨道交通领域多通道、多部位、多方向的振动数据中,取得了良好成效。
本文针对国内某地铁车辆运行振动水平较大问题,基于车辆运行过程中关键部位如轴箱、构架、车体的振动加速度实测数据,应用约翰逊法则和GJB/Z126-1999 两种方法对振动数据进行归纳,对比两种方法的区别,与标准IEC 61373-2010《机车车辆设备冲击振动试验》[10]中轨道车辆装备振动的标称值进行对比,结合振动环境归纳谱分析车辆的分层传递率,根据以上结果分析车辆振动水平较大的原因,具有一定的工程意义。
1 谱归纳原理
对车辆真实振动环境进行恰当的归纳处理,需对多通道的测量数据进行参数假设检验[3],将属于同一总体的数据归并(1.1 节将做介绍),形成特征样本,对特征样本按照预定的置信度和分位点估计容差上限,可得实测谱,对特征样本进行频段划分(1.2节将做介绍),对各频段内的特征样本按照预定的置信度和分位点估计容差上限,可得规范谱。
1.1 通道归并
计算所有数据通道的PSD(Power Spectral Density)功率谱密度,记为(i,j)(i=1,2,…L1;j=1,2,…,M1;k=1,2,…,N1),其中L1为测量通道数,M1为样本容量,N1为谱线数。对于第i个通道的RMS(Root Mean Square)均方根值,按式(1)进行均值和方差估计。

选取其中任意通道i和通道m,按式(2)计算统计量Fn(i,m)和tn(i,m)。

假设通道i和通道m的PSD 属于同一总体,则Fn(i,m)服从自由度为(M1-1,M1-1)的F分布,tn(i,m)服从自由度为2(M1-1)的中心t分布,在给定的置信度1-α下,若式(3)成立则假设成立。

将同一总体的数据通道PSD 进行归并,形成特征样本(p,q)(p=1,2,…P1;q=1,2,…,Qp),其中P1为特征样本数,Qp为特征样本容量。特征样本(p,q)为随机振动环境条件归纳处理的基本数据。
1.2 谱线归并

对相邻谱线的均值(p)和方差(p)按式(5)计算统计量Fn(k,k+1)和tn(k,k+1)。
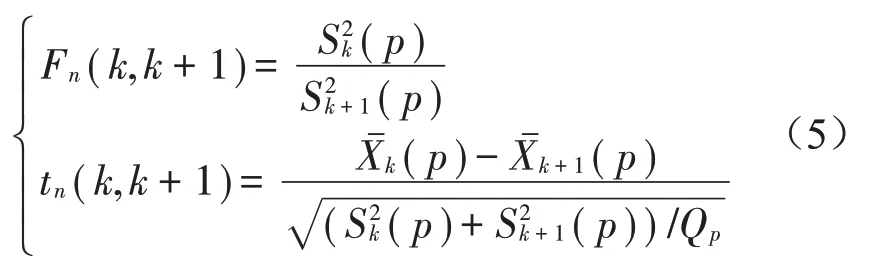
假设相邻谱线k和k+1 的PSD 属于同一总体,则Fn(k,k+1)服从自由度为(Qp-1,Qp-1)的F分布,tn(k,k+1)服从自由度为2(Qp-1)的中心t分布,在给定的置信度1-α下,若式(6)成立则假设成立。

对属于同一总体相邻谱线进行归并,形成H1个频段,h频段两侧谱线号为a,b(h=1,2,…,H1),谱线总数Nh为b-a+1。
2 归纳方法原理
为确认轨道车辆振动数据的正态随机性,应检验样本的平稳性、各态历经性、正态性,在工程应用中,在样本数量足够大的前提下,近似认为振动数据满足平稳性和各态历经性[11],数据归纳流程如图1所示。通过第1节分析得到通道归并后的特征样本并进行频段划分,对归并数据选用合适的归纳方法(2.1节、2.2节将做介绍),可得到随机振动的环境归纳谱(归纳谱包括实测谱和规范谱),其中实测谱是连续谱图,规范谱是将属于同一总体的相邻谱线归并,谱图呈现阶梯状分布,标准谱为IEC61373-2010 中轨道车辆装备振动的标称值,将归纳谱与标准谱对比,评估车辆的振动水平。

图1 谱归纳流程
2.1 GJB/Z126-1999数据归纳方法
对于正态分布的随机振动数据,归纳方法选用GJB/Z126-1999 数据归纳方法,按式(7)计算置信度为1-α,分位点为β的容差上限系数Fs。对通道归并或谱线归并后的特征样本按式(8)进行容差上限估计得到振动环境条件随机振动归纳谱G(p)。
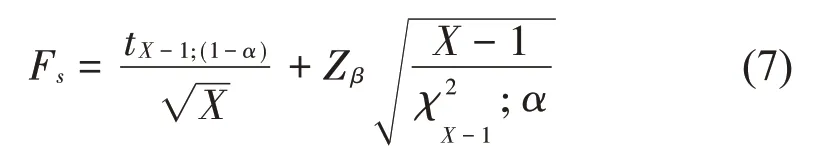
式 中:Zβ为满 足Prob[Z≤Zβ]=β的正态分布分位点;

2.2 约翰逊法则
对于非正态分布的随机振动数据,归纳方法选用约翰逊法则,按式(9)实现非正态分布样本数据x到标准正态分布样本数据z的转换。

约翰逊曲线共有3种转换形式[6],选用合适的曲线形式进行拟合是非常重要的,一般使用样本的分位值来选择约翰逊曲线的拟合形式并进行未知参数的估计,取4个对称的、等距离的标准正态偏差:-3Z,-Z,Z,3Z,理想的Z值范围为0.05~1.25[12],根据Z值计算原样本的分位值x-3Z、x-Z、xZ、x3Z,按式(10)计算参数m、n、p,根据mn/p2与1 的大小选择曲线形式,对应的3种约翰逊曲线分布形式如式(11)所示。

选定分布曲线的形式后,根据所选Z值和m、n、p值可求出分布曲线参数ε、η、γ、λ的估计值。置信度为1-α,转换后标准正态分布的分位点Zβ应与原样本数据的分位点FV对应,如式(12)所示,通过求该式的反函数,即可得到非正态样本数据在置信度为1-α下的数据上限,如式(13)所示,其平方形式即为相应非正态分布的随机振动数据谱归纳结果,如式(14)所示。

3 基于实测数据的谱归纳分析
3.1 实验设计
针对国内某地铁车辆运行振动水平较大问题,为掌握在实际线路中整备状态下车辆的振动特性及振动传递关系,以一节动车为研究对象,车辆以AW3 工况运行,即地铁车辆超员载荷(9 人/m2),实测中,在一位端空气弹簧上方车体布置两个测点(列车前进方向的前端),12个构架测点,分别位于一位端一位侧构架的中部和端部(列车前进方法的前端右侧)、一位端二位侧构架的中部和端部(列车前进方法的前端左侧),在一位端构架轴箱处布置了4个测点,部分测点如图2所示,为覆盖车辆系统的主振频率,采样频率设置为2 048 Hz,采样方向为横向和垂向。

图2 测点布置图
3.2 数据分布的正态性
时域样本可分为多样本、多通道,采用改进周期图(Welch)法对各数据通道进行功率谱密度计算,施加海明窗,重叠系数为3/4,FFT(Fast fourier transform)快速傅里叶变换分析点数为采样频率的两倍,频率分辨率为0.5 Hz。对功率谱密度进行正态检验是非常有必要的[13-14],选取某通道单个频率点的功率谱密度数值,原样本分布直方图如图3(a)所示。图中曲线为符合样本均值和方差的正态分布曲线,可看出原样本数据分布不符合正态规律,经过约翰逊法则变换后的频数分布图如图3(b)所示。数据分布与正态曲线贴合较好。

图3 约翰逊拟合样本前后直方图
为检验转换后数据与标准正态分布的偏离程度,引入卡方检验,公式如下:

式中:Ai为i水平的观察频数,n为总频数,pi为i水平的期望频率,k为单元格数。
上述转换过程所选取z=0.35,mn/p2=0.84。经统计,样本频数、期望频数和卡方统计量如表1 所示。得到χ2=6.461,数据共有8组,从样本中确定了4个参数,故自由度为8-4-1=3,取α为0.05,则=7.815,说明SB分布曲线能较好拟合这批数据,转换后数据分布较好地贴近正态分布。

表1 样本频数、期望频数和卡方统计量
3.3 谱归纳分析结果
以轴箱垂向振动为例,根据上述理论采用GJB/Z126-1999数据归纳方法和约翰逊归纳法则的不同归纳结果如图4至图5所示。分别以G和Y表示,标准谱以S表示。

图4 轴箱垂向振动实测谱对比

图5 轴箱垂向振动规范谱对比
可看出,用约翰逊法则求得的实测谱和规范谱都略高于GJB/Z126-1999数据归纳方法,原因是非正态数据没有确定的分布规律,直接求取分位点不能正确估计样本数据,通过约翰逊法则转换为正态分布后的分位点反求原数据的分位点能更好地反映样本总体的真实分布。在频率为60 Hz 附近时,采用约翰逊法则实测谱拟合上限值已经超出标准谱,规范谱接近标准谱限值,与车辆实际振动水平较大现象相符,因此,运用约翰逊法则进行数据归纳能够更好地贴合工程实际。
应用谱归纳原则,可得轨道车辆的一系悬挂分层传递率T1(f)和二系悬挂分层传递率T2(f),公式如下:

式中:Sa(f)、Sf(f)、Sc(f)分别为轴箱、构架、车体的谱归纳结果,同时可根据IEC61313中的标准谱计算得到标准传递率,表示为IEC传递率。
以一系悬挂垂向传递率为例,如图6 所示。在频率为11 Hz~36 Hz范围时其传递率数值均在1之上,在频率为28 Hz、56 Hz、162 Hz、429 Hz处均有局部极点,在频率为28 Hz处传递率达到最大值3.9,导致车辆构架振动水平较大,也说明了车辆的一系传递对振动的衰减效果不好,需要进行参数优化。

图6 一系悬挂垂向传递率
4 结语
(1)本文应用了约翰逊法则归纳某地铁车辆振动数据,与GJB/Z126-1999 数据归纳方法对比,发现构架振动环境恶劣,应用约翰逊法则时在60 Hz附近的归纳实测谱值超过IEC61373 标准谱。基于归纳谱分析车辆的分层传递率,发现车辆的一系悬挂垂向传递效果不佳。
(2)指出约翰逊法则能够更好地贴合工程实际,可用于多部位、多通道的数据归纳,对振动故障诊断具有较好的参考价值。
