双重单面碰撞调谐质量阻尼器参数优化及减振性能分析
2021-10-22王文熙王修勇
李 欣,王文熙,王修勇,张 静
(1.湖南科技大学 结构抗风与振动控制湖南省重点实验室,湖南 湘潭411201;2.湖南大学 风工程与桥梁工程湖南省重点实验室,长沙410082)
调谐质量阻尼器(Tuned mass damper,TMD)作为一种研究较为成熟的阻尼器在土木工程中得到了大量的应用[1-3]。但其只有在调谐的时候才能有较好的控制效果,一旦发生失谐时则其减振效果会明显下降[4]。为了改善TMD 这一不足之处,一些学者将碰撞耗能引入TMD设计中,提出了碰撞调谐质量阻 尼 器(Pounding tuned mass damper,PTMD)。PTMD以黏弹性材料代替传统TMD中的阻尼,研究表明PTMD 相较于TMD 有更好的鲁棒性[5]。Xue等[6]将PTMD 用于单层框架和多层框架的振动控制,并进行振动台试验。李英娜等[7]研究地震作用下PTMD对海洋平台的振动控制,与TMD进行比较发现PTMD 的控制效果更好。Lin 等[8]以广州电视塔为工程背景,建立有限元模型分析了PTMD 对多自由度结构的振动有着良好的抑制效果。Yin 等[9]将PTMD 应用于风荷载、交通荷载以及桥梁耦合系统的振动控制中,安装PTMD 后桥梁的竖向位移显著降低。Wang 等[10]为了更好地利用碰撞耗能,在PTMD 的基础上取消一个限位挡板,并将碰撞间隙取为0,提出了单面碰撞调谐质量阻尼器(Singleside pounding tuned mass damper,SS-PTMD)。Wang等[11]通过风洞试验验证了SS-PTMD对桥梁的涡振有着良好的控制效果。Duan 等[12]将SS-PTMD应用于阻尼器位移空间有限的主结构上,并与传统PTMD 的减振性能比较。结果表明SS-PTMD 有更好的性能和更大的应用前景。何禹忠等[13]设计了悬臂式SS-PTMD 控制单自由度结构振动。仿真和实验研究表明SS-PTMD在调谐与失谐14%、21%时,结构阻尼比分别增加3.85%、2.35%以及1.65%,表明SS-PTMD有较好的鲁棒性。
本文考虑到SS-PTMD 与TMD 的类似之处,基于Wang等[10]提出的SS-PTMD力学模型及碰撞力模型,将单个SS-PTMD的研究延伸向双重单面碰撞调谐质量阻尼器(Double single-side pounding tuned mass damper,DSS-PTMD)的减振分析。通过仿真分析研究了DSS-PTMD 的优化参数和在自由振动与简谐激励下的减振性能。
1 DSS-PTMD-结构耦合方程
单自由度结构安装DSS-PTMD 的力学模型如图1所示,系统的运动方程可写为:
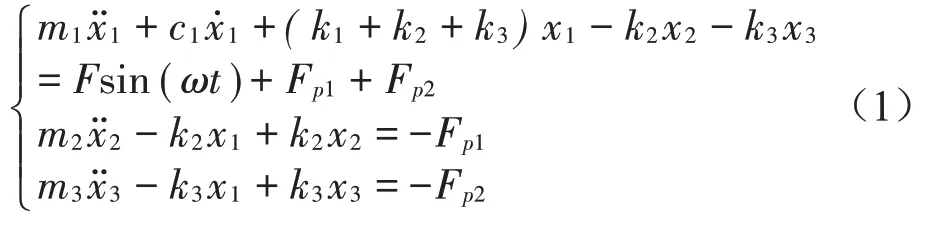
式中:m1、c1、k1分别为主结构的质量、阻尼和刚度;x1分别表示主结构位移、速度及加速度;m2、k2分别为1#SS-PTMD 的质量和刚度,x2、为1#SSPTMD 的位移和加速度;m3、k3分别为2#SS-PTMD的质量和刚度,x3为2#SS-PTMD 的位移和加速度;Fsin(ωt)是外部激励;Fp1和Fp2分别为1#PTMD、2#PTMD与主结构之间的碰撞力,其表达式为[10]:

其中:δ为碰撞过程中质量块嵌入黏弹性材料的位移,其1 阶导数为速度;n为非线性指数;k为碰撞刚度;ζ为碰撞阻尼因子;δmax和δe分别为碰撞嵌入黏弹性材料的最大位移和碰撞结束后的黏弹性材料残余变形;fe为最大弹性碰撞力,其具体表达式为:

根据能量守恒原理,式(2)中3个模型参数满足下列方程[10]:
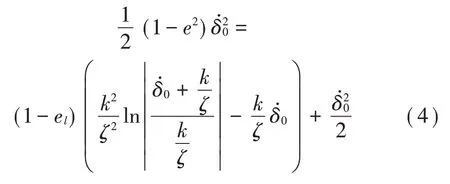
式中:el为残余变形率,el=δe/δmax,el与e的关系为[14]:

式中:β=0.938。
2 SS-PTMD最优参数分析
DSS-PTMD的优化参数包括最优频率比和最优阻尼比,对于图1所示力学模型,两个单面碰撞调谐质量阻尼器的固有频率及阻尼比为[10]:
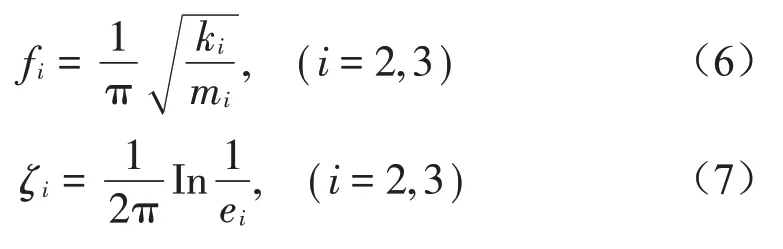
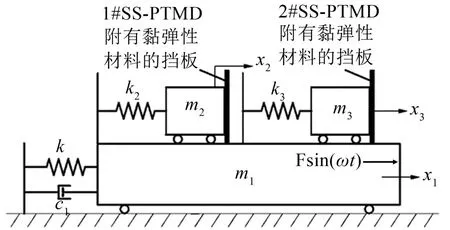
图1 DSS-PTMD与主结构耦合力学模型
定义频率比为:
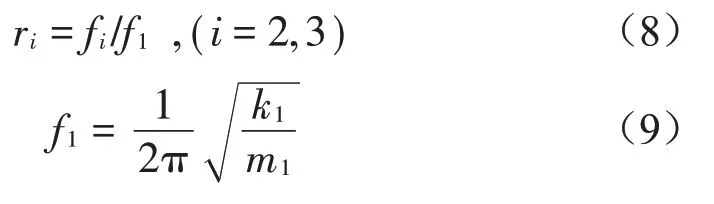
基于H∞优化准则,DSS-PTMD的参数优化目标函数可表示为:
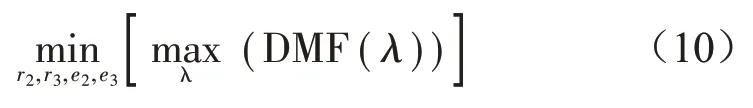
式 中:λ为外部激励频率,DMF(Dynamic magnification factor)为位移动力放大系数,定义为:

式中:X1(λ)为主结构在简谐荷载作用下的稳态响应幅值,F为激励幅值。
为了研究DSS-PTMD 优化参数,针对图1 模型进行了仿真分析。主要参数为:m1=45 kg、f1=2.91 Hz、ζ1=0.5 %。为方便计算,1#SS-PTMD 与2#SSPTMD的质量、碰撞刚度、非线性指数取为相等。其中m2和m3为结构质量和质量比乘积的一半,碰撞刚度k=6.5×105N/m1.5,非线性指数n=1.5。
仿真分析得到的DSS-PTMD 最优参数及相应的DMF 如表1 所示。为了比较DSS-PTMD 与SSPTMD 的控制效果,表1 中给出了相同质量比条件下SS-PTMD的优化参数和DMF。
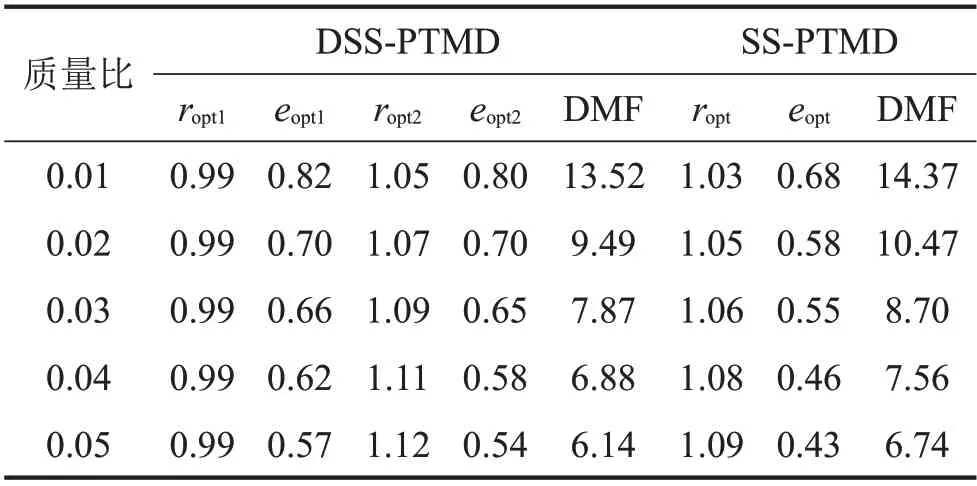
表1 DSS-PTMD及SS-PTMD优化参数
从表1 可以看出,随着质量比的增加,DSSPTMD 的最优频率比ropt1没有发生变化,而ropt2呈现逐渐增大的规律变化;最优恢复系数eopt1和eopt2均呈现逐渐减小的规律变化,且两者数值基本相等;DMF逐渐减小,且减小的趋势趋于缓和。在相同的质量比情况下,DSS-PTMD 所对应的DMF 均小于SS-PTMD。表明DSS-PTMD在最优控制的情况下,其减振效果优于SS-PTMD。
3 DSS-PTMD减振性能分析
3.1 自由振动
主结构和DSS-PTMD 的仿真参数依旧与上节相同,DSS-PTMD 的最优参数取总质量比3 %所对应的最优频率比和最优恢复系数。自由振动的初始条件为:初始位移为20 mm,初始速度为0。分别讨论主结构频率完全调谐、主结构频率失谐±5 %和±10%时的减振效果。
图2 为主结构无控、SS-PTMD 控制以及DSSPTMD 控制的仿真效果。在完全调谐的情况下,无控、SS-PTMD和SS-DPTMD控制时的结构阻尼比分别为0.5%、4.05%及4.31%。当频率失谐-5%时,SS-PTMD 和DSS-PTMD 对应结构等效阻尼比为2.6%及2.69%;频率失谐+5%时,SS-PTMD和DSSPTMD对应结构等效阻尼比为4.72%及4.73%。当频率失谐-10%时,SS-PTMD 和DSS-PTMD 对应结构等效阻尼比为1.8%及1.61%;频率失谐+10%时,SS-PTMD 和DSS-PTMD 对应结构等效阻尼比为3.34 %及3.3 %。由此可以看出在完全调谐或者小失谐的情况下,DSS-PTMD 对自由振动的抑制效果优于SS-PTMD,反之,当失谐过大时,SS-PTMD的效果更佳。还可以看出,对这两种阻尼器而言,负向失谐对减振效果的影响要比正向失谐更严重。

图2 自由振动时,SS-PTMD与DSS-PTMD的控制结果
3.2 简谐激励
当主结构所受到幅值为10 N的简谐激励时,图3 给出了无控、SS-PTMD 及DSS-PTMD 控制时简谐荷载作用下的结构幅频响应图。完全调谐时,SSPTMD和DSS-PTMD控制时的动力放大系数幅值为8.70和7.87,与无控时的动力放大系数幅值99.28相比,最不利情况下的减振率为91.24 %和92.07 %。频率失谐-5 %时,SS-PTMD 和DSS-PTMD 控制时的动力放大系数幅值为13.44 和13.11,与无控时相比,最不利情况下的减振率为86.46 %和86.79 %。频率失谐+5 %时,SS-PTMD 和DSS-PTMD 控制时的动力放大系数幅值为13.26 和12.56,与无控时相比,最不利情况下的减振率为86.64 %和87.35 %。频率失谐-10%时,SS-PTMD和DSS-PTMD控制时的动力放大系数幅值为20.18 和21.61,与无控时相比,最不利情况下的减振率为79.67 %和78.23 %。频率失谐+10%时,SS-PTMD和DSS-PTMD控制时的动力放大系数幅值为18.95 和21.72,与无控时相比,最不利情况下的减振率为80.91 %和78.12 %。由此可知,在完全调谐和失谐较少时,DSS-PTMD的减振效果优于SS-PTMD,当失谐过大时则情况相反,这与自由振动的结论是一致的。
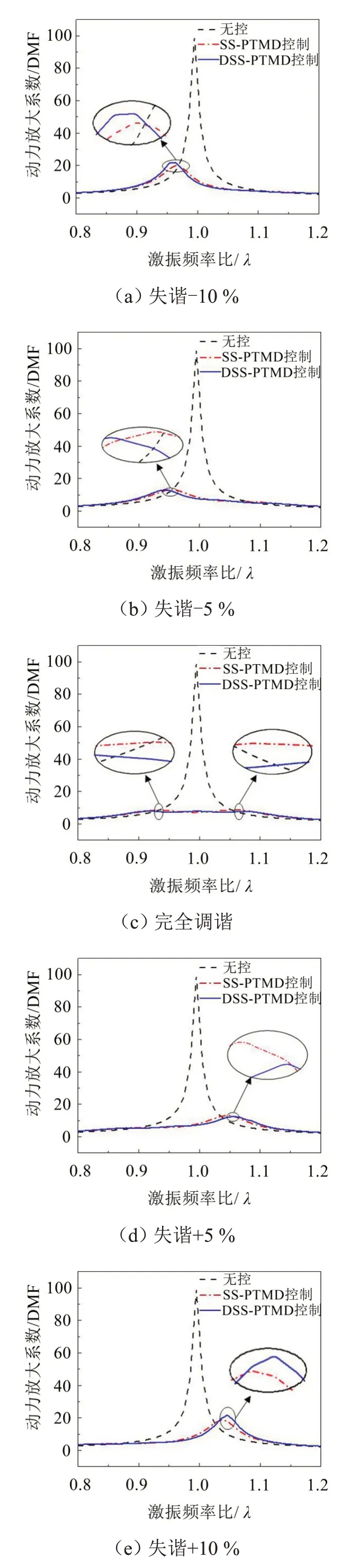
图3 SS-PTMD与DSS-PTMD控制的幅频响应曲线
4 结语
本文建立了单自由度结构-双重单面碰撞调谐质量阻尼器力学模型。以动力放大系数为优化指标进行参数优化,讨论了完全调谐时SS-PTMD 与DSS-PTMD 的振动控制效果。分析了SS-PTMD 和DSS-PTMD 在自由振动与简谐激励下的减振性能。得出如下结论:
(1)通过数值优化得出了SS-PTMD 与DSSPTMD 的最优参数,发现在最优参数下DSS-PTMD的减振效果优于SS-PTMD。
(2)DSS-PTMD 和SS-PTMD 对结构有良好的振动控制效果。当频率失谐时,减振效果虽有下降,但其对自由振动和简谐振动仍有较好的抑制效果。
(3)当频率失谐较小时,DSS-PTMD 的减振效果优于SS-PTMD。反之当失谐较大时,SS-PTMD减振效果更优。
