含非均匀介质覆盖层吸声特性研究

董天韧，胡昊灏，陈 杨

(江苏科技大学 船舶与海洋工程学院，江苏 镇江212003)

吸声系数是表征含空腔覆盖层声学特性的基本参数，直接计算变截面空腔覆盖层的声特性较复杂，因此通常采用分层等效近似的方法，将变截面空腔视为多个圆柱腔。

常用的近似方法主要包括解析法和数值法，各种分析方法的之间也存在明显的差异。高晓琴[1]，Chang等[2]将空腔层中橡胶单元近似为高粘性液体，分析了平面波在垂直入射和斜入射情况下含空腔覆盖层的声学性能，但论文只考虑了法向传播的纵波而忽略了其它波的影响，也未考虑空腔谐振对声学特性的影响。白国锋等[3]利用传递矩阵模型，同时考虑了纵波和横波，更接近于平面波传播的实际情况。但是这种方法只适用于均匀介质，无法计算介质中含有空腔的情况。刘志宏等[4]分析了背衬对覆盖层声特征的影响，但未研究含空腔覆盖层的声特征，也没有讨论参数变化对吸声性能的影响。张浩等[5]在分层介质传递矩阵模型的基础上，引入界面面积因素，使模型可以计算具有内部空腔的覆盖层吸声性能，但文中并未对比空腔类型对覆盖层吸声性能的影响。冯常慧等[6]，赵宏刚等[7]和Ivansson[8]将空腔作为黏弹性介质中的散射体，运用分层介质多重散射理论分析覆盖层的声学特性，但该方法只能局限于少数几种简单几何形状空腔的黏弹性层。

数值法[9-12]主要使用有限元和边界元等方法，将空腔作为散射体，计算不同类型的声学覆盖层的声特征，数值计算不受覆盖层内空腔形状的限制，但是当对结果精度要求较高时，需要较长的计算时间。

针对以上问题，本文对含变截面周期空腔的声学覆盖层声吸收性能展开研究，空腔分布方式如图1所示，空腔沿X、Y方向周期分布。利用周期边界条件取一个单元进行分析，在此基础上将空腔部分沿厚度方向均匀分成若干层(如图2所示)，当分层的厚度足够薄时，各层变截面空腔等效为均匀圆柱空腔。利用弹性波传播理论，结合应力连续边界条件求得等效波数，最后采用二维传递矩阵法得到声学覆盖层的吸声系数。

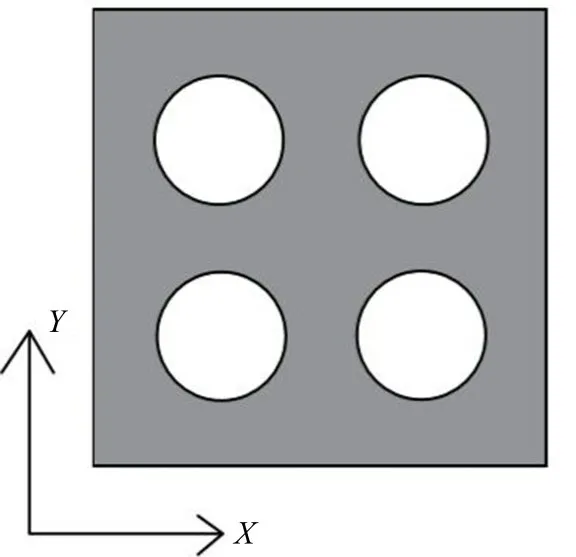
图1 空腔分布示意图

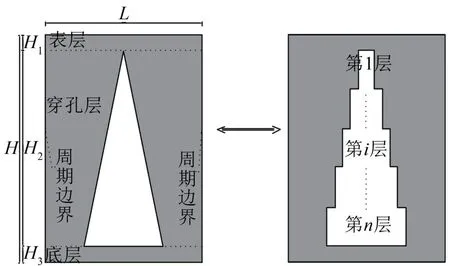
图2 分层近似示意图

1 分层等效理论

取图2 中分层近似后多段均匀圆柱腔的第i段分析，如下图3 所示。设覆盖层内部圆柱径为ai、覆盖层半径为b。

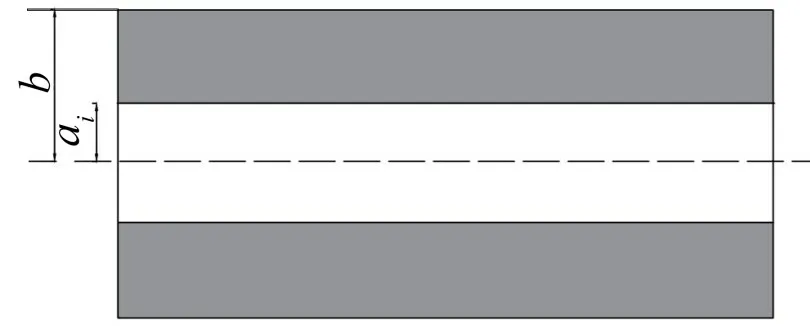
图3 第i层覆盖层示意图

为了求得圆柱空腔单元中的等效波数，首先引入弹性波在覆盖层中传播的运动方程：

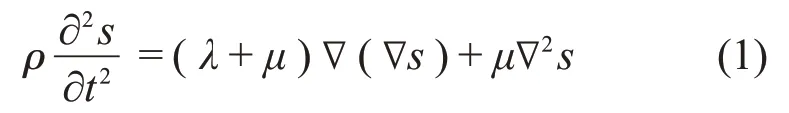
式中：s为位移矢量，λ，μ为Lame 常数，ρ为橡胶密度，∇，∇2分别为Hamiltonian 算子和Laplace 算子。位移s可以表示为标量场φ的梯度和矢量场ψ的旋度的和，即：

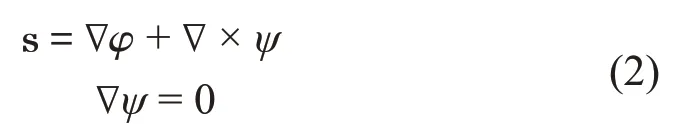
式中：φ为纵波势函数，ψ为横波势函数。矢量势函数可以写成标量势函数，故公式(2)可以表示为：

式中：kl为纵波波数；ks为横波波数。

公式(3)的形式解可以表示为：

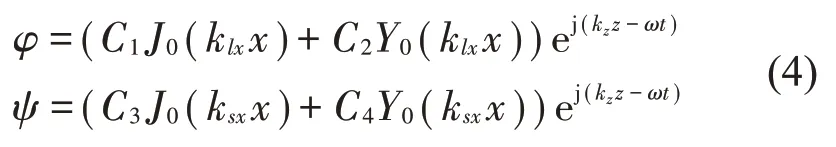
式中：C1,C2,C3,C4为待定系数，klx=为轴向波数，J0,Y0分别为第一类和第二类贝塞尔函数。

柱坐标下径向位移sx和轴向位移sz为：

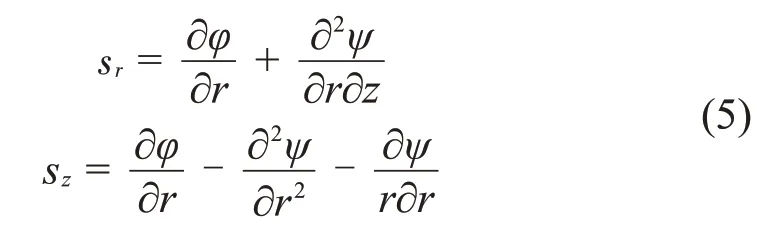
柱坐标下应力和应变的关系为：

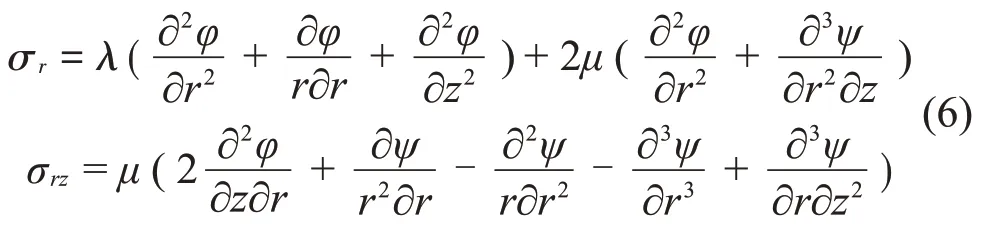
考虑边界条件，在空腔内界面处，由于腔内介质为空气，因此认为内界面的边界条件为‘绝对软’边界，所以空腔内侧的应力边界条件为：

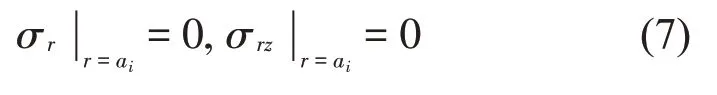
在空腔的外界面，由于运动是同步的，所以界面处应力为零，轴向的位移为零，则空腔外侧的边界条件：

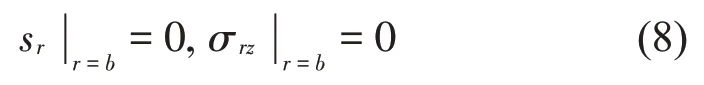
联立公式(4)、式(5)、式(6)和边界条件公式(7)、式(8)可得：

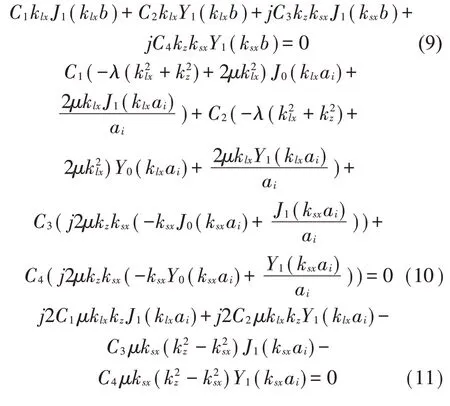
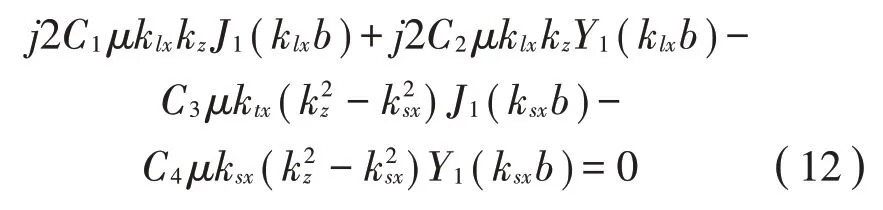
上述方程为齐次线性方程组，待定系数C1,C2,C3,C4有非零解的充要条件为方程组的系数行列式等于零，通过对其系数行列式求解，即可得到声波在第i层沿轴向传播的波数kiz，第i层覆盖层的等效密度为橡胶密度和空气密度的体积平均值：

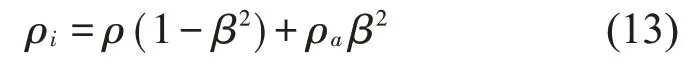
式中：ρi为等效后密度，ρ为基体材料密度；ρa为空气密度，β=ai/b。

2 声吸声系数

在得到各层等效参数以后，由各层相邻两侧声压和质点振速连续建立一个传递关系，并用矩阵表示，利用传递矩阵计算含圆锥空腔覆盖层的声特征，其表达式为：

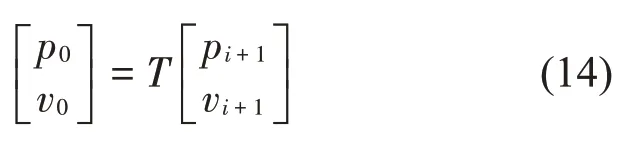
式中：

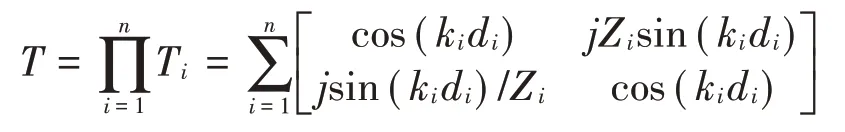
式中：di为第i层厚度，ki为第i层波数，Zi为第i层阻抗，p0,v0为覆盖层前界面声压和振动速度，pi+1,vi+1为覆盖层背面界面的声压和振动速度。

本文中声学覆盖层两端均为无限大水域时，其透射Tr、反射Re和吸声系数A分别为：

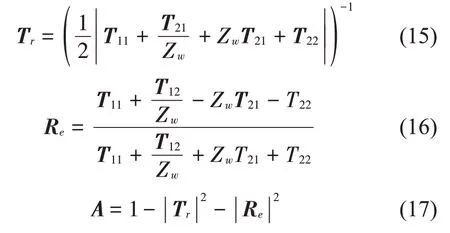
式中：Zw为水的阻抗，T11,T12,T21,T22为式(14)中传递矩阵T的元素。

3 方法验证

为了验证分层近似法求解声吸收的正确性，采用声学有限元软件建立含锥形空腔的声学覆盖层周期单元（如图4 所示），分析过程考虑钢背称对声吸收的影响，并利用PML(完美匹配层)模拟无限大水域。覆盖层单元尺寸L=30 mm，H=50 mm，H1=H3=5 mm，圆锥空腔尺寸：底面直径10 mm，高H2=40 mm。覆盖层材料参数为：泊松比σ=0.49，杨氏模量E=7.1×107Pa，损耗因子η=0.2，密度ρ=1100 kg/m3。

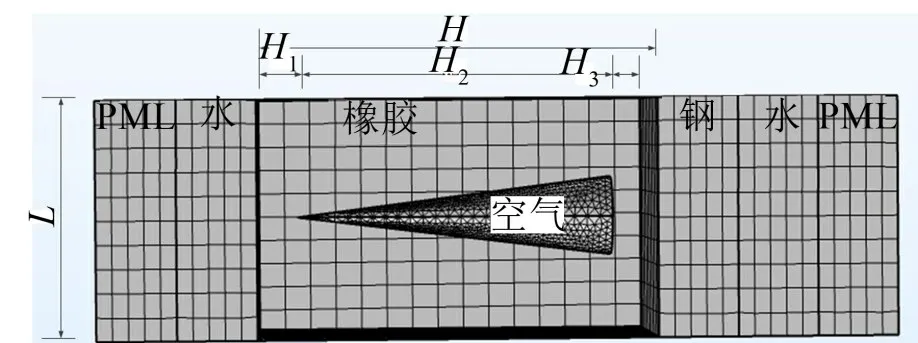
图4 周期单元声吸收有限元模型

平面波从左侧水域垂直入射，入射频率为0.1 kHz～9 kHz，步长0.1 kHz，解析和数值计算结果如下图5所示。

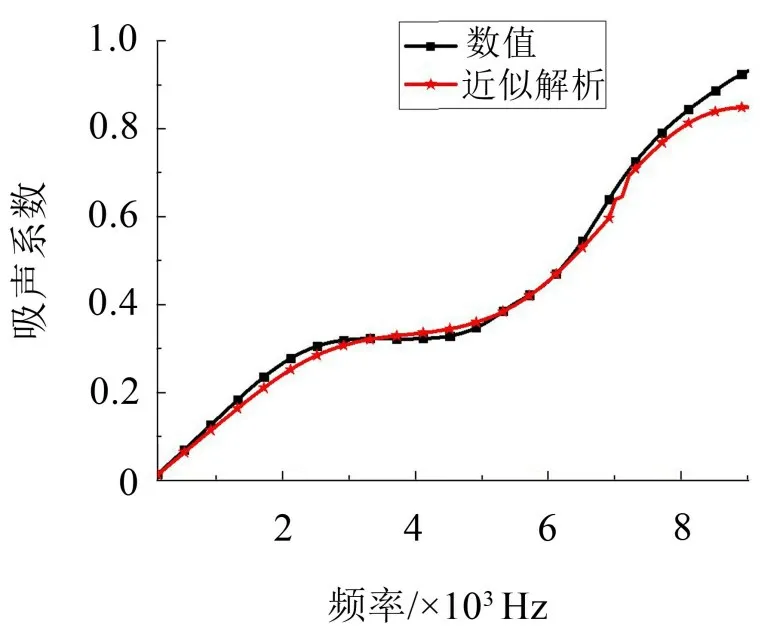
图5 近似解析和数值对比

由图5近似解析和数值计算的吸声系数对比图可知，频率在8 kHz 之后，两种计算结果出现偏差。出现偏差的原因可能是：

①本文使用分层近似法计算变截面空腔的吸声系数，计算过程中分层数量不合理，导致高频时出现偏差；

②解析方法中选取的周期覆盖层单元为圆柱形，但是本文有限元软件所建立的模型为长方体，两种不同边界形状覆盖层单元，在计算结果上存在一定的区别。从整体上来说，两种方法计算的吸声系数曲线吻合较好，说明本文采取的解析程序是有效的。

4 参数分析

本节以图4模型为例分析不同参数下覆盖层的吸声性能，为了分析含周期圆锥空腔的声学覆盖层吸声机理，下面对相关参数展开分析，主要包括弹性背衬，圆锥腔尺寸和空腔形状等参数对吸声系数的影响。

4.1 背衬对吸声系数的影响

弹性背衬结构由于特性阻抗与覆盖层差异较大，会对入射波在介质中的传播产生较大的影响，进而影响吸声性能，如图6所示。

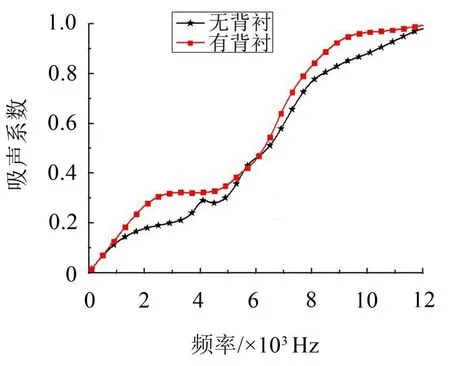
图6 背衬对吸声系数的影响

从图6 可以看出有、无背衬对覆盖层的声吸收有重要影响，有弹性背衬的覆盖层吸声系数在大部分频率范围要高于无背衬的情况。文献[13-14]分析了背衬对圆柱空腔覆盖层吸声性能的影响，论文指出：背衬与覆盖层材料声阻抗失配，入射声波经过覆盖层后，被背衬与覆盖层的耦合面反射回覆盖层中，形成二次吸收，从而提高吸声性能。

为了更清晰地给出背衬的影响，下面分别分析有、无背衬时，f=4 kHz 和f=9 kHz 处覆盖层位移云图。如图7所示。

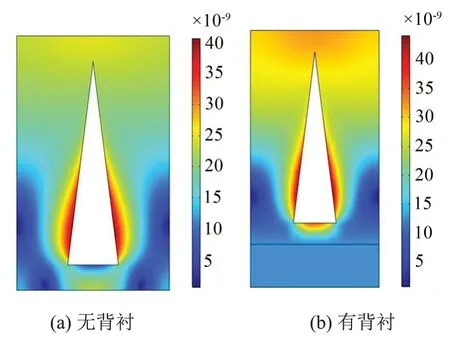
图7 f=4 kHZ位移图

图7 覆盖层位移云图的图例范围为(5～40)×10-9mm，由图可知，在该频点下，有背衬的位移幅值大于无背衬。并且覆盖层基体从底部到顶部，位移幅值逐渐增大，说明覆盖层整体被拉伸或者压缩，因此低频时覆盖层的吸声是由基体的共振引起的。

图8 覆盖层位移云图的图例范围为(5～40)×10-9mm，由图可知，在该频点下覆盖层内部空腔的位移幅值远大于基体的位移，说明高频时覆盖层的吸声依赖于空腔的共振。

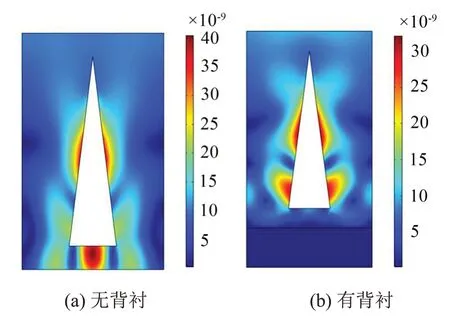
图8 f=9 kHz位移图

由以上分析可知，背衬不仅会提高含圆锥空腔覆盖层的吸声性能，还会影响覆盖层基体及空腔的共振频率，从而改变覆盖层吸声峰值频率。

4.2 圆锥腔尺寸对吸声系数的影响

圆锥腔体尺寸的改变，会影响腔体的共振频率。图9给出了不同底面半径的圆锥腔对吸声系数的影响，由图可知，腔体半径改变会使吸声峰值频率产生偏移，这为在感兴趣频率范围设计覆盖层声吸收提供了参考。

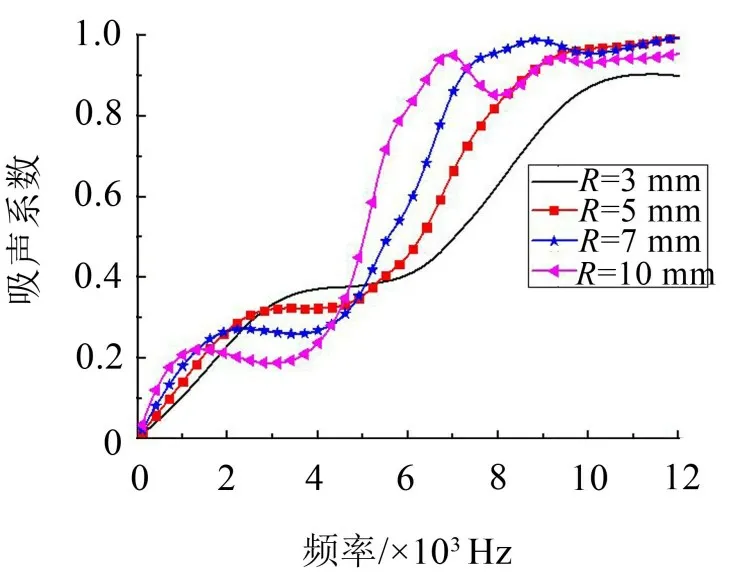
图9 圆锥腔半径对吸声系数的影响

下面将分析圆锥空腔半径影响吸声峰值频率发生偏移的原因。上文分析可知,第一（低频）吸声峰值依赖于基体的振动，由图10 基体位移幅值图可知，当圆锥空腔半径增大后，基体之间厚度变薄，更易产生变行，从而使共振频率向低频移动，故随空腔半径的增加第一吸声峰频率减小。

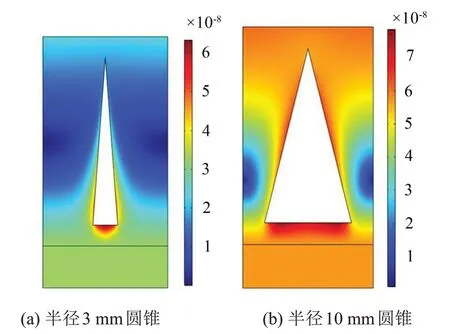
图10 覆盖层1 kHz位移图

图10 和图11 覆盖层位移云图的图例范围为(1～6)×10-8mm，由图11 可知，圆锥空腔位移幅值随半径的增大而增加，这是因为使空腔发生共振的声波波长与空腔半径成正比，当空腔半径增大时，共振频率声波波长增大，所以空腔产生共振的频率降低，而第二(高频)吸声峰由空腔的振动引起，故随着空腔体积的增加吸声峰频率降低。

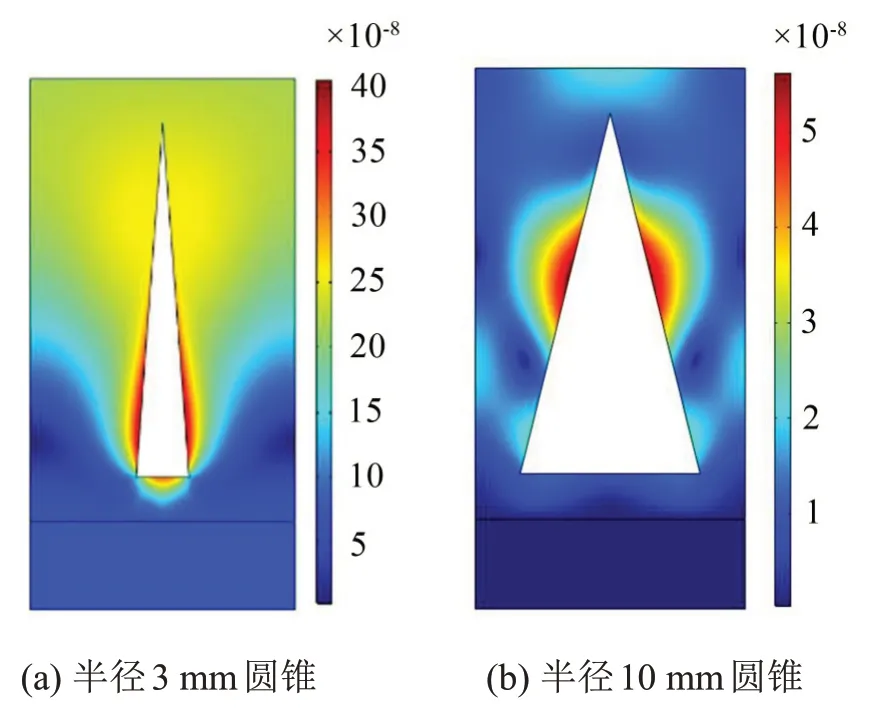
图11 覆盖层6 kHz位移图

4.3 空腔形状对吸声系数的影响

将圆锥空腔换成图12圆台形空腔，圆台底部半径5 mm，顶部半径3 mm，高40 mm。

图12 圆台形空腔

从图13可知，圆台空腔的吸声峰值频率小于圆锥空腔，是因为平面波沿空腔表面传播过程中纵波会转变为剪切波，当空腔体积增加后，提高了纵波转变为剪切波的比例，从而增大了声波的能量损耗，提高了覆盖层吸声性能，因此随着空腔体积的增大吸声峰值频率向低频偏移。

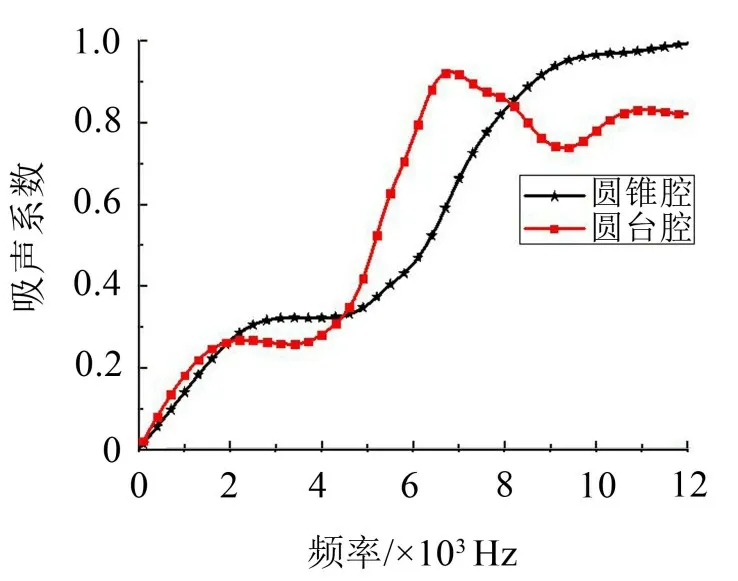
图13 吸声系数对比

4.4 杨氏模量对吸声系数的影响

图14给出杨氏模量对覆盖层声吸声的影响，当覆盖层的杨氏模量增大后，吸声曲线峰值向右移动，说明当杨氏模量增大后，引起空腔和基体共振的频率也随之增大。

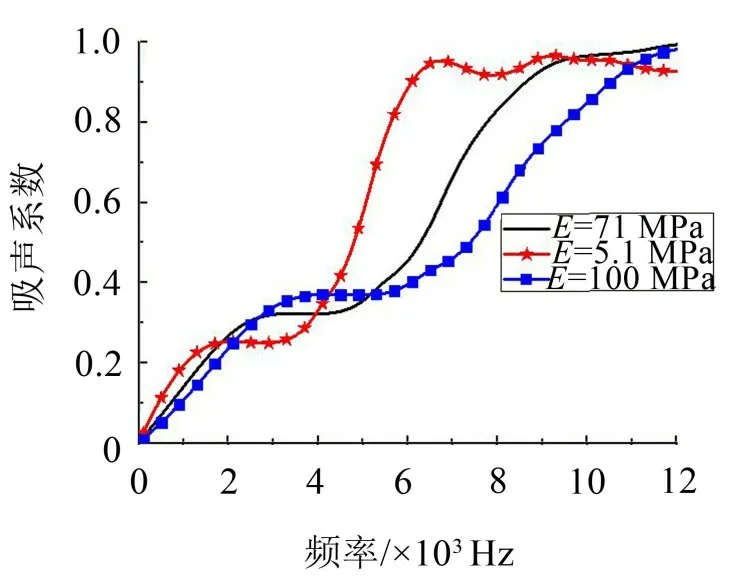
图14 不同杨氏模的吸声系数

4.5 入射角度对吸声系数的影响

本节分析平面波入射角度对覆盖层吸声性能的影响，下图15为声波入射示意图。

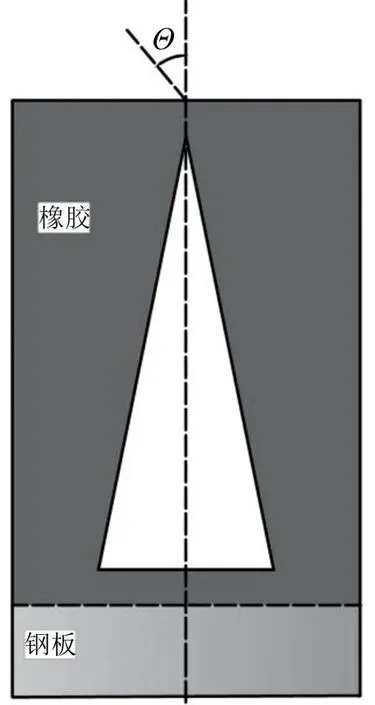
图15 平面波入射示意图

图17 是在吸声系数曲线0.7 kHz 处，平面波垂直和75°入射时覆盖层位移云图，云图图例范围为(1～7)×10-8mm，对比图17(a)、图17(b)两图可知，斜入射时覆盖层出现更大的横向变形，这是因为橡胶的横波损耗因子远大于纵波损耗因子，因此平面波斜入射产生的能量损耗远大于垂直入射。这也是图16 低频时吸声系数随着入射角度增加而增大的原因。

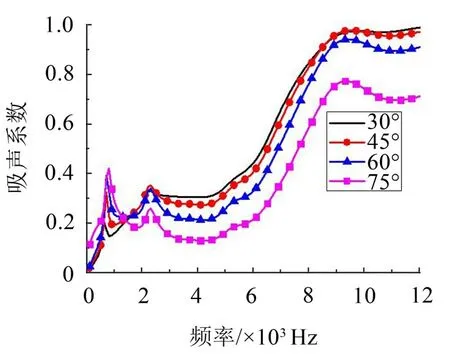
图16 不同入射角度下吸声系数

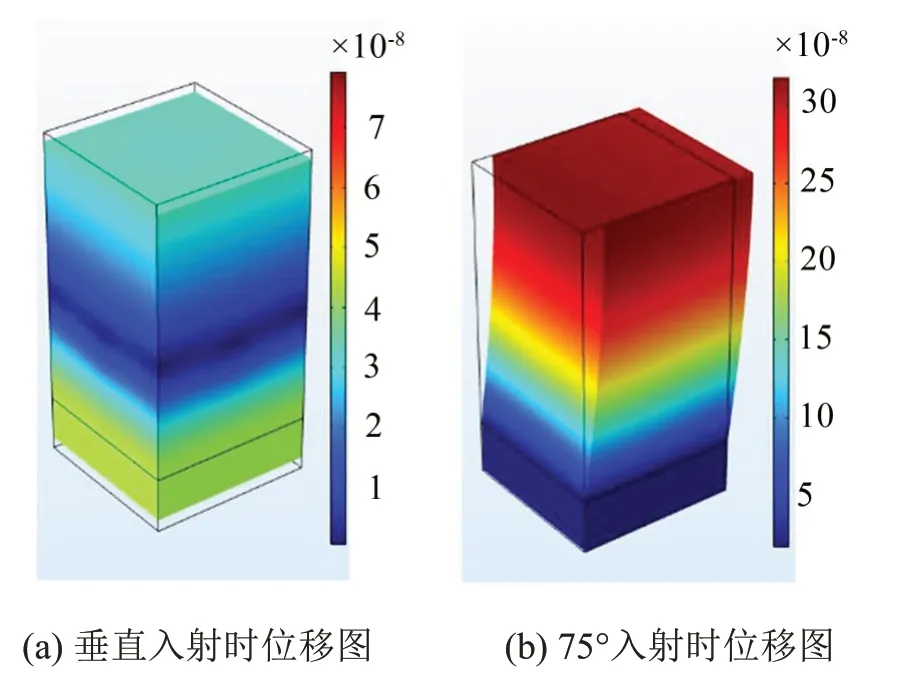
图17 覆盖层位移图

以平面波60°入射时的吸声曲线为例，分析0.7 kHz和9.2 kHz处吸声峰值的物理机理。

图18为覆盖层吸声峰值处位移图，云图的图例范围(1～30)×10-8mm，由图可知，第一吸声峰(0.7 kHz)时覆盖层基体位移较大，说明覆盖层被整体地拉伸或压缩，此时的吸声峰值是由基体的振动引起的。第二吸声峰(9.3 kHz)时圆锥空腔振动幅度较大，而覆盖层整体位移幅值很小，说明高频时的吸声峰值主要依赖于覆盖层内部空腔的共振。

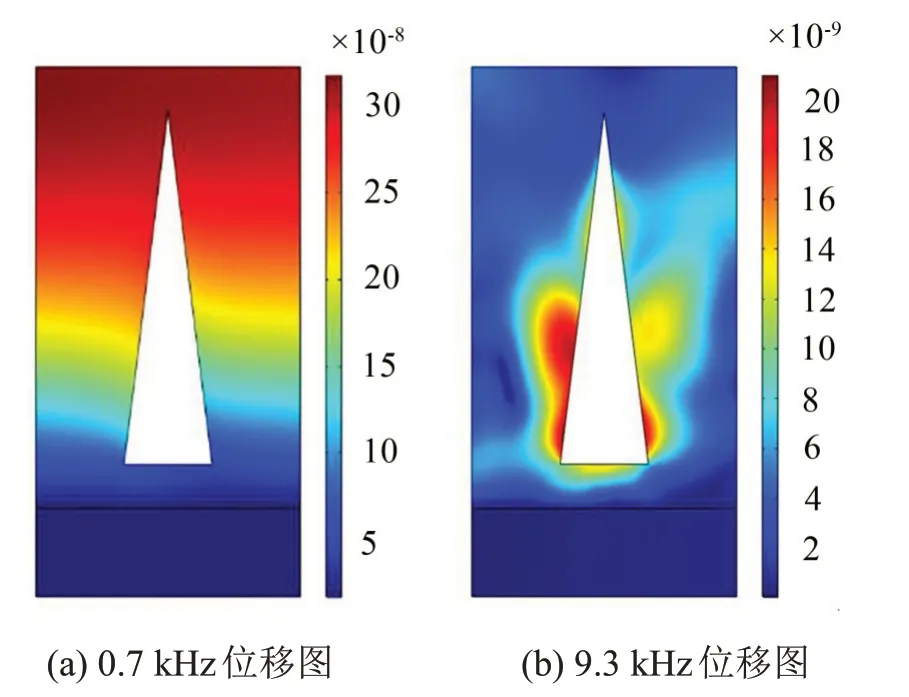
图18 吸声峰值位移图

5 结语

本文针对含周期圆锥空腔声学覆盖层声吸收问题，利用等效分层介质理论，重点分析了覆盖层内空腔尺寸、空腔形状、基体材料参数、背衬和平面波入射角度等对覆盖层吸声性能的影响，得出以下几点结论：

(1)用数值法求解含空腔覆盖层的吸声特性，可以和解析解计算结果相吻合，证明了本文方法的可靠性；

(2)背衬是影响覆盖层吸声性能的重要因素，有背衬时吸声性能在大部分频率范围要好于无背衬的情况；

(3)覆盖层材料参数，空腔直径，空腔形状等对声吸收有重要影响，计算结果表明：空腔直径越大，基体杨氏模量越小，吸声峰值频率越向低频移动。可以通过设置以上参数，提高覆盖层在低频段的吸声系数；

(4)平面波斜入射时，低频时吸声系数峰值随入射角度的增加而增加，声吸收物理机理与垂直入射类似。