基于能量分析法对阻尼钢板声辐射的优化研究
2021-10-22刘杰昌常光宝李书阳
刘杰昌,常光宝,李书阳,鄢 亮
(1.上汽通用五菱汽车股份有限公司,广西 柳州545007;2.上海桓领信息科技有限公司,上海201101)
随着社会的不断发展,在汽车、飞机、铁路运输和船舶行业内振动和噪声问题受到越来越多的关注[1]。当前被动振动和噪声控制应用非常广泛,其中阻尼衰减技术[2-3],由于其结构简单、低成本、方便布置等优点,得到了广泛的工程应用。通常根据阻尼材料铺设的形式分为自由阻尼(Free Layer Damping,FLD)和约束阻尼(Constrained Layer Damping,CLD)结构。
自由阻尼结构就是将阻尼材料贴附在钢板上形成的结构[4]。而约束阻尼结构像三明治一样,两侧部分为钢结构,中间部分为阻尼层[5]。它们的振动衰减机理一样,都是随着钢板的振动而发生变形,并将获取得到的动能转换成热能,进行能量的耗散,实现振动的衰减。
目前,对阻尼钢板结构优化的研究有许多[6-7],主要是根据结构的力学特性,确定阻尼材料的最优布局。杨德庆等[8-9]提出了阻尼胞单元和阻尼拓扑敏度等概念,建立了基于阻尼拓扑敏度综合评价的阻尼材料拓扑优化准则,并用于频率和动响应约束下自由阻尼层结构阻尼材料的配置优化;徐伟等[10]郑玲等[11]根据经典薄板理论,建立约束阻尼钢板的有限元模型,推导出其辐射声功率及灵敏度公式。以声功率最小的优化目标,采用渐进式优化算法,得到约束阻尼材料的最优优化结构。王超等[12]设计了两种典型的阻尼薄板复合结构,在3种边界条件下,阻尼薄板复合结构的振动特性,从模态应变能角度分析了复合结构的阻尼损耗因子的精度,对降低结构振动,改善辐射噪声有着较为重要的工程应用意义。
在汽车领域由于自由阻尼结构简单、制作工艺方便、成本低等优势有着广泛的应用。在该背景下,本文研究一块铺满阻尼材料的钢板,在考虑真实的激励输入的情况下,采用渐进式优化算法以阻尼材料的体积分数为约束条件进行仿真计算,得到阻尼钢板辐射声场中目标区域的声功率能量,将不同位置对应的声功率能量值映射到阻尼钢板上,最终得到该阻尼钢板的敏感度分布云图,并采用仿真和试验进行验证优化结果。本方法从声功率角度出发,为结构噪声设计提供了一种重要的技术手段。
1 阻尼钢板仿真建模及优化
1.1 离散系统振动微分方程介绍
对自由阻尼钢板,其主要分析环节为阻尼材料对阻尼钢板的振动性能的影响,在建模过程中,需要对阻尼材料的阻尼效果进行准确的建模;对于结构件来说,采用有限元分析理论,将结构等效为多自由度系统进行简化,并采用多自由度系统的强迫振动方程进行描述,如式(1)所示;

其中:M为质量矩阵,C为阻尼矩阵,K为刚度矩阵,P(t)为施加载荷。
对于黏弹性阻尼材料,其阻尼特性可以简化为线性阻尼,因此在其阻尼参数处理的过程中,将采用线性等效的质量矩阵及刚度矩阵进行简化,因此对于阻尼材料本身,其将采用复模量及密度进行参数表征。
根据离散系统振动微分方程,将黏弹性阻尼材料采用线性多自由度系统方程进行简化,最终对黏弹性阻尼材料的参数表征体现为复模量及其密度;而采用国标GB 18258[13]中提到的结构损耗因子η对阻尼材料的阻尼性能进行表征,其与阻尼材料的复模量之间的关系式(2)所示:

式中:Ei表示为耗能模量;Er表示为储能模量。因此,阻尼材料的复模量可以与结构损耗因子进行相互转换,从而作为结构有限元分析及建模的输入。
1.2 阻尼板声辐射计算
将平板表面离散成N个面积相等的小单元,每个单元面积为Δs。由于每个单元面积都很小,假设每个单元内的速度处处相等,这样就可以利用单元内某一点的振动速度代表整个小单元的振动速度。
平板辐射声场[14]内某点a的辐射声压可以表示为:
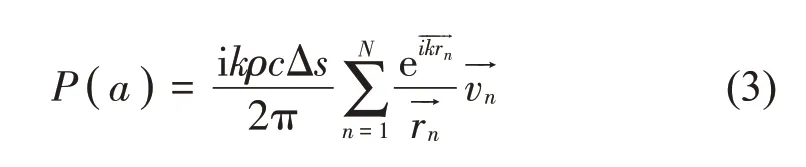
式中:P(a)表示场点a处的声压;i=;ρ表示空气密度;c表示声波在空气中的传播速度;k表示波数表示声压频率表示声源上某点n到场点位置a的位移矢量表示声源表面法向的振速矢量。
2 阻尼钢板声辐射仿真及优化
考虑到乘用车的应用背景,同时避免环境噪声对阻尼钢板优化结果的干扰,故建立一个类似车厢式封闭的箱体进行阻尼仿真分析,如图1(a)所示。
采用Nastran 和Actran 软件进行联合仿真进行优化分析,Nastran软件分别对结构和声腔进行模态计算,然后在Actran中读取模态结果,搭建模态叠加法的仿真模型。基于Python语言编程对Actran进行优化仿真计算。
2.1 阻尼板箱体模型
在Actran中建立边长为1 m的立方体有限元网格模型,其中把箱体金属外壳看作为壳单元,厚度为2 mm,材料为#304 不锈钢。箱体内部含有吸声棉,并通过驻波管对吸声棉进行吸声系数进行测试,获取吸声棉的声学参数。其中阻尼钢板如图1(b)所示,其中采用半功率带宽法[13]对阻尼材料进行测试,获取阻尼材料参数。
在Actran 中建立有限元仿真模型,如图1(a)所示,在箱体阻尼钢板的外表面上一点,输入0~500 Hz的白噪声激励,在箱体内几何中心处布置一个麦克风监测点。

图1 阻尼板声辐射FEA模型
2.2 阻尼板仿真分析优化
阻尼板的仿真优化是在Actran 软件基础上,采用Python 语言进行二次开发的的一个过程,具体的优化技术路线如图2所示。
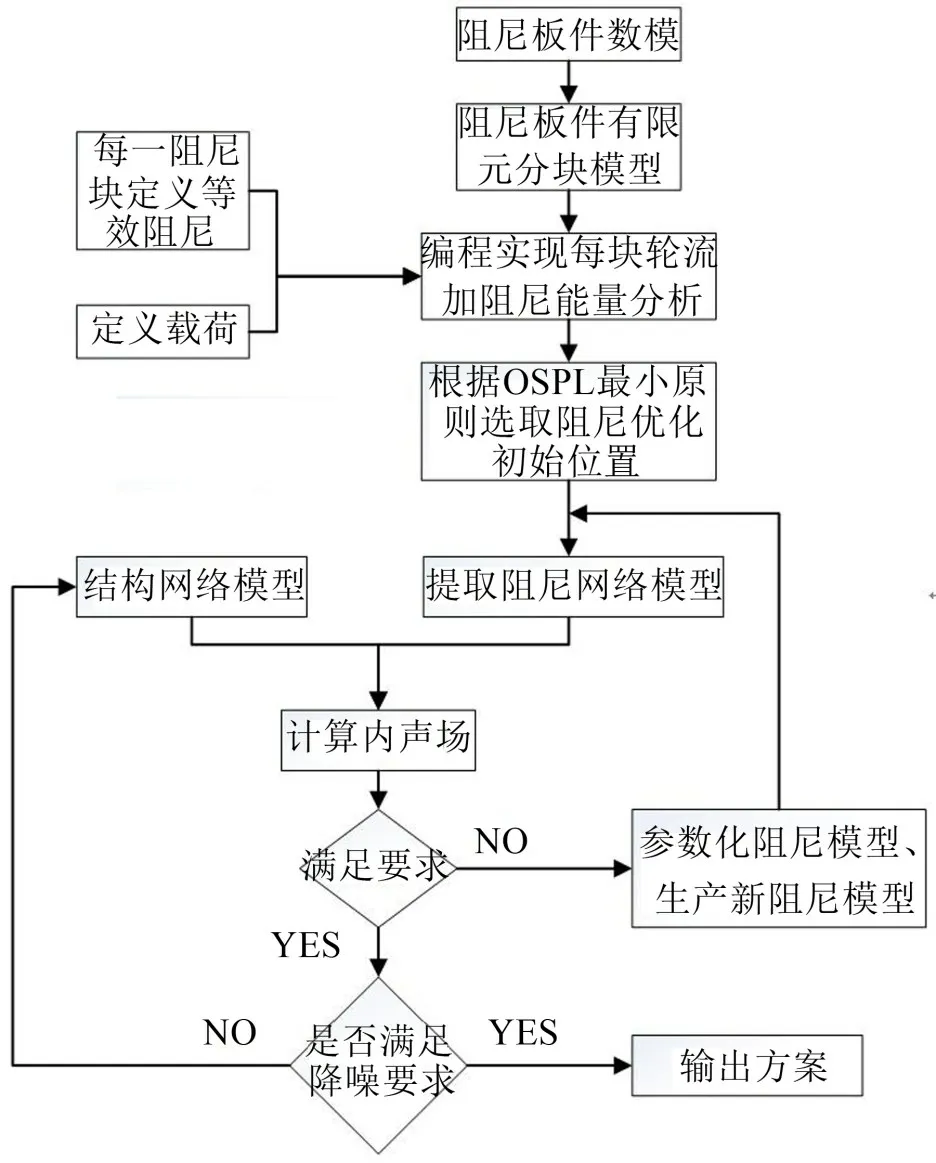
图2 阻尼板优化技术路线
首先对阻尼钢板有限元网格模型进行分块,对应软件中每一个块内的网格数量。本文按9个单元为一块进行划分,规定每一块阻尼称胞元,共计64个胞元,并进行编号,如图3(a)所示。然后通过编程控制,轮流给每个胞元定义一个等效阻尼系数0.4。然后在箱体外侧施加0~500 Hz 的白噪声激励,步长为1 Hz,进行声功率能量计算,则箱体内的麦克风监测点得到不同胞元所得到的响应结果。
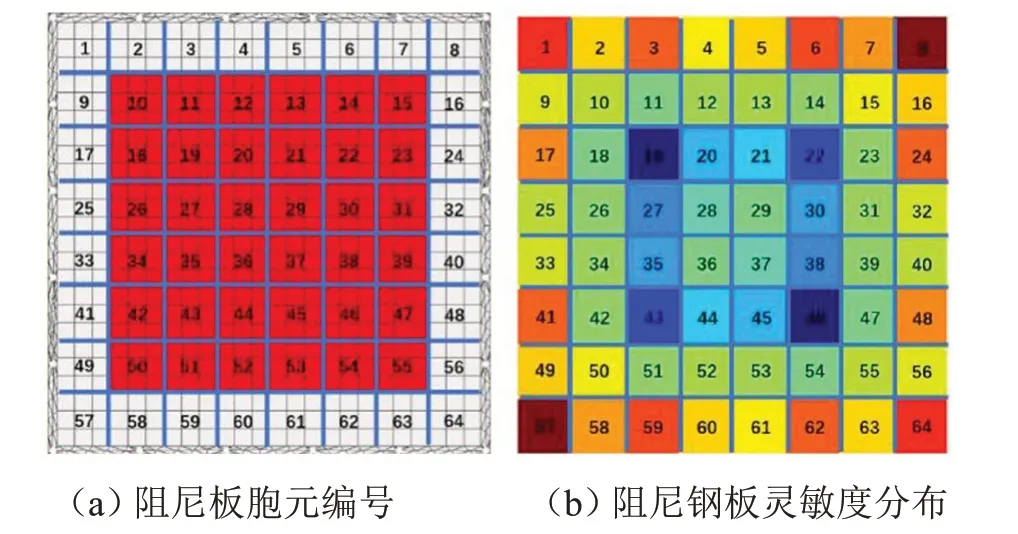
图3 阻尼板模型
最后将这些结果映射到对应的胞元上,形成阻尼钢板灵敏度云图分布,如图3(b)所示。其中颜色越浅表明越敏感。根据全局声压级(Overall Sound Pressure Level,OSPL)最小的原则,将64个胞元对应的能量结果,按从小到大进行排序。在质量不变的前提下,选择全局优化函数,参数化阻尼单元,并约束全局声压级小于原设计,且阻尼材料厚度为均匀分布,设定最大迭代次数,优化目标为降噪,在优化计算过程中,不同数量的胞元,就有相应的厚度。
其中当胞元数量为25,阻尼厚度为4.32 mm,阻尼材料的位置分布如图4所示。该种布局达到很好的降噪效果。
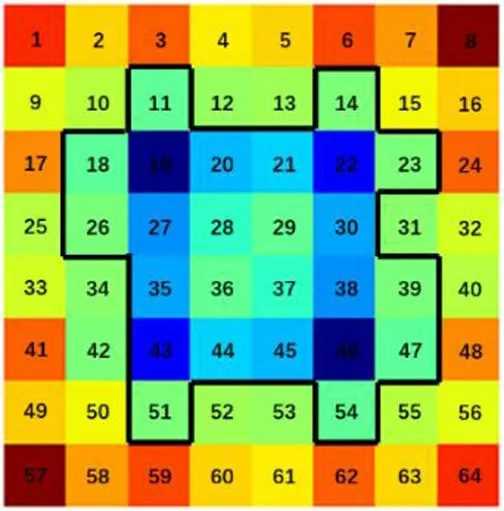
图4 优化后阻尼模型
在Actran 软件中建立仿真模型,同时考虑声振耦合效应,对优化的阻尼模型进行噪声响应仿真分析,阻尼仿真模型如图5所示。

图5 Actran仿真模型
建立优化前阻尼模型仿真箱体和优化后阻尼模型仿真箱体,在激励点输入试验测得的0~500 Hz的白噪声信号,建立声振耦合边界设置,进行模态叠加法仿真分析,在箱体内部的同一坐标设置为麦克风监测点。通过计算,含优化前阻尼模型箱体内麦克风监测点处的全局声压级为98.80 dB,含优化后阻尼模型箱体内麦克风监测点处全局声压级为96.70 dB。采用能量分析法对阻尼钢板进行优化,实现了2.10 dB的降噪效果,如图6所示。

图6 优化前与优化后声压级对比
3 阻尼箱体试验验证
3.1 阻尼噪声测试台介绍
按照仿真优化后的阻尼钢板尺寸,制作一张阻尼钢板,如图7(a)所示。同时,阻尼钢板箱体的噪声试验平台和仿真模型一样,其中包含阻尼钢板、304不锈钢金属外壳和吸声棉等部分,阻尼钢板与箱体之间的连接采用密封胶泥进行减振和密封处理,并采用螺栓固定连接,如图7(b)所示。

图7 阻尼板辐射噪声测
在信号发生器内定义信号输入,使激振器产生频段为0~500 Hz的白噪声,作用在阻尼钢板上,同时通过力传感器进行采集激励信号。在箱体的几何中心布置一个麦克风传感器,使用LMS数据采集仪进行声辐射信号的采集。
3.2 仿真和试验数据验证
通过上述试验,力传感器得到激励输入的频谱信号,考虑上文做阻尼材料布置优化的激励输的频谱信号与本次试验的信号有一定差异,所以在仿真中更换为本次试验中测得的激励输入信号作为新的激励输入,并进行仿真计算。最后将仿真得到的阻尼钢板声辐射频谱信号和试验得到的阻尼钢板声辐射频谱信号进行对比,如图8所示。
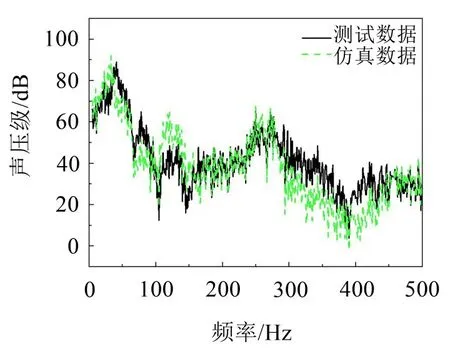
图8 仿真与测试结果对比
对试验中麦克风传感器测量的时域数据进行傅里叶变换,不采用倍频程合成,而是计算0~500 Hz频域内的全局声压级为95.82 dB,仿真得到的麦克风测点的全局声压级为96.70 dB,误差为0.88 dB。从图中也可以看出仿真和测试有着较好的一致性。
4 结语
本文采用能量分析法对阻尼钢板声辐射的优化,在不改变质量的情况下,对阻尼材料分布区域进行合理优化,实现降低声辐射的优化目标。并且本文中的优化方法,是基于Actran软件的二次开发,为工程应用提供一种重要的手段。
(1)基于Actran软件进行二次开发,对阻尼板进行分块,并使用渐进优化算法逐步计算每小块的振动灵敏度,进而得到一种优化模型。
(2)基于优化后的模型,编程对厚度曲行参数优化,控制阻尼单元模型的生成,并约束声辐射小于原设计,优化目标为降噪,从而达到降噪的效果,此过程可以找出合理厚度。
(3)根据优化算法得到的优化模型,进行试验验证,通过试验和仿真数据的对比,确认了仿真的精度以及优化方法的合理性,为阻尼优化在工程的应用提供了一种重要的技术手段。
