应用数值模型评估复合型材填充硬质泡沫的声学影响

陈红伟，王 奇

（北京声望布莱纳咨询有限公司，北京100029）

型材结构在建筑，高铁，地铁的设计中有广泛的应用，尤其是在机车设计时，大部分的车体结构都是型材结构。型材结构刚度大，质量轻，同时有很好的承载性能。然而单独型材结构的隔声性能通常很不理想，一般高铁和地铁应用的型材隔声量只有27 dB左右，因此很多工程师研究通过在型材的空隙中填充泡沫来增加结构的隔声性能。然而填充的泡沫对结构整体的质量，阻尼，刚度均有影响，而结构的隔声量是这些因素的综合结果，并不能简单的从理论分析得到结论。本文采用混合模型的数值分析方法对影响隔声量的各个因素进行分析，评估填充硬质泡沫对型材结构的声学性能的影响。

1 影响声学性能的关键参数

型材结构在声激励载荷下，能量从接受侧表面经由肋板传递至辐射侧表面，引起结构的振动进而向空气辐射噪声。结构的辐射效率和振动速度是影响结构隔声量的两个关键参数。本文首先对两个参数及隔声量进行简单介绍。

1.1 辐射效率

辐射效率描述了结构辐射噪声能力的水平，可以通过结构辐射声功率Wrad与结构表面均方振动速度(v)的平方以及辐射面积S来定义。

其中：ρ0和c0代表空气的密度和声速。只有当结构的弯曲波波长大于空气波长时，结构表面才能有效地辐射噪声[1]。当结构的弯曲波波长与空气波长相等时，结构的辐射效率最大，对应的频率fc称为吻合频率。图1 显示了不同厚度铝板的波数和辐射效率，可以看到铝板厚度增加结构弯曲波波数减少，吻合频率向低频移动，吻合频率以下的辐射效率增加。结构的辐射效率在吻合频率以下主要受到边界条件的影响，吻合频率以上，结构的表面声辐射占主要部分[2]。

图1 6 mm铝板和4 mm铝板弯曲波波数及辐射效率对比

1.2 振动速度

结构在声载荷的作用下产生振动速度，振动速度的大小与结构本身的能量以及质量有关。

其中：E代表结构子系统的总能量，m代表子系统的质量。

当系统达到平衡时，输入能量等于损耗能量，即Pin=ηωm(v)2，公式说明一定的输入能量下结构的质量和阻尼越大，其振动速度越小。

1.3 隔声量

隔声量是结构的固有特性，描述了给定结构的隔声性能。隔声量的定义是入射到结构的声能和透过结构声能比的分贝数[3]，其数学表达式为：

式中：Wt为透射声功率，Wi为入射声功率。忽略由质量控制路径传递的能量，认为透射的声功率完全是结构的振动辐射产生的，则有：

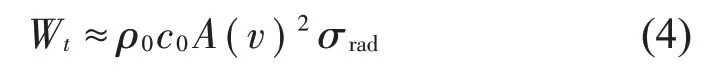
其中：A代表了结构的辐射表面积，v代表结构的均方振动速度，σrad代表了结构的辐射效率。说明在相同的入射能量下，结构的振动速度和辐射效率越小其隔声量越大，反之则隔声量越小。

2 理论介绍和模型创建

2.1 混合模型理论介绍

研究振动噪声的模型方法包含有限元法(Finite Element Method，FEM)和统计能量法(Statistical Energy Method，SEA)，两种方法分别适用于解决低频和高频问题。这两种方法的缺点是都不能解决中频振动噪声问题，基于此Shorter 等提出了FE-SEA混合建模的方法来解决结构振动噪声的中频问题[4]。

FE-SEA建模中，结构分为有限元子系统和统计能量子系统。刚度大，模态数少的结构建为有限元子系统；刚度小，模态数多的结构建立为统计能量子系统。系统的响应可以表示为：

其中：Dt为有限元子系统的刚度矩阵，Sff代表激励力互谱为子系统k的平均刚度矩阵，Ek为子系统k的振动能量，nk为子系统k的模态密度；ω表示圆频率。各个子系统能量平均，则FE-SEA 耦合系统的功率平衡方程写成：

2.2 创建混合模型

本文分析的复合型材样件结构的尺寸为1 m×1.13 m，中间斜筋的厚度为1.5 mm，上下表面根据斜筋的分割位置厚度分别为2 mm和3.5 mm。上下面板之间的高度为78 mm，斜筋之间的上间距为137.8 mm，下间距为236.8 mm。复合型材的弹性模量为1.15×105MPa，密度为1 600 kg/m3，中间泡沫的弹性模量为60 Mpa，密度为100 kg/m3。

根据样件的实际结构创建混合模型如图2 所示。其中图2(a)和图2(b)分别为填充泡沫前后的混合模型，混合模型与实际的样件尺寸相同，型材结构采用二维的壳单元模拟，中间的泡沫结构采用三维实体单元建模，型材结构和泡沫结构的单元节点互相耦合。采用半无限自由场来模拟结构向空气的辐射噪声[5]，混合模型受到有限元结构的模态影响，因此采用1/24 倍频程分析45 Hz～4 000 Hz 的频率结果。

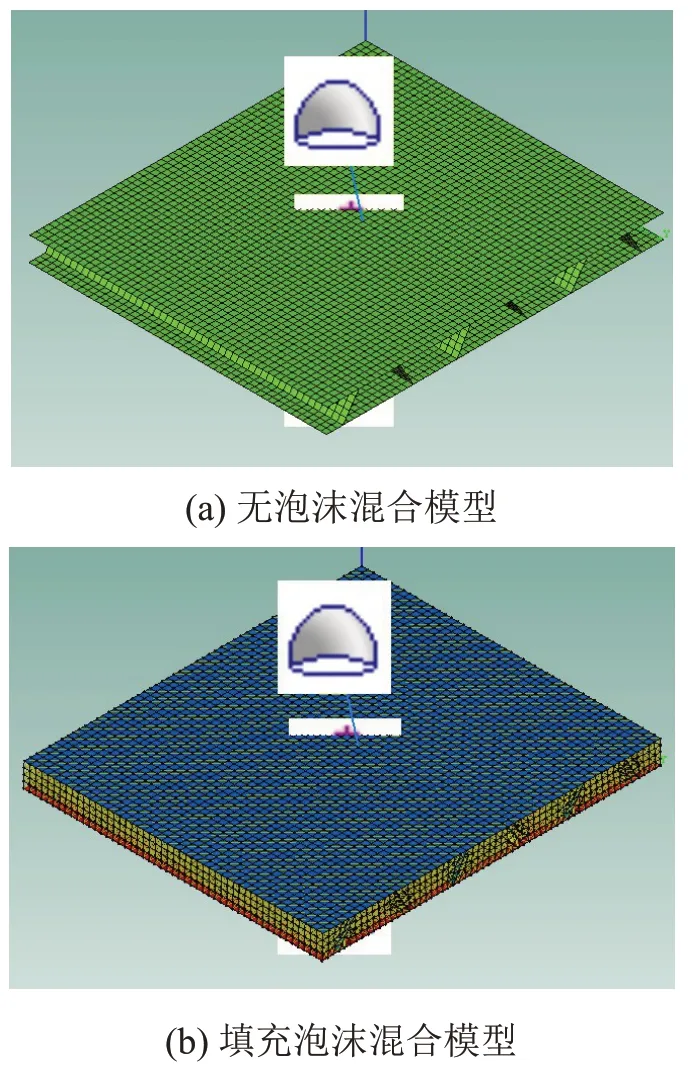
图2 有无填充泡沫型材的混合模型

3 基于模型的声学参数分析

3.1 填充泡沫对结构辐射效率的影响

图3的混合模型结果显示了填充泡沫前后结构表面辐射效率的变化。250 Hz以下受到边界条件的影响，辐射效率变化不大；250 Hz～3 500 Hz 之间，填充泡沫使得辐射效率明显上升。根据1.1 节辐射效率的理论可知辐射效率与结构的弯曲波波长和空气波长的吻合度有关，填充的泡沫增加了结构的整体刚度使得结构弯曲波波长增加，此时辐射效率上升。3 500 Hz以上有无填充泡沫结构的弯曲波波长都大于空气波长，此时两者的辐射效率均接近于1[1]。

图3 有无泡沫辐射效率的变化

3.2 填充泡沫对结构振动速度的影响

图4 显示了填充泡沫前后上下面板的振动情况，从图4(a)模型的分析结果看，在填充泡沫前，上下面板在200 Hz以下的振动速度基本一致，表现为图5(a)的整体模态振型；在200 Hz 以上上面板和下面板的振动速度开始分离，两者的振动速度具有较大的差异，说明两者的耦合度减弱，表现为图5(b)的局部模态振型。从图4(b)的分析结果看填充泡沫之后上下面板的振动直到2 000 Hz之后才出现分离的特征，这表示填充泡沫之后使得结构在2 000 Hz 以下表现为图5(c)的整体模态振型；2 000 Hz以上时上下面板才开始表现为图5(d)的局部模态振型。增加的泡沫明显增强了型材结构和泡沫的耦合作用，使得模态分离频率由200 Hz上升至2 000 Hz。

图4 有无填充泡沫上下面板振动情况

图5 有无填充泡沫时结构部分模态振型

透射声能主要是辐射面的振动辐射出的噪声，因此需要对有无泡沫上下面板的振动速度分析。

图6 显示了相同载荷（1 Pa 声载荷）作用下填充泡沫前后辐射面（上面板）的振动速度的变化。可见在400 Hz 以下填充泡沫后上面板振动速度明显下降（主要原因为泡沫增加了质量和刚度），而在400 Hz～1 000 Hz区域除了部分峰值点填充泡沫的振动速度大于无泡沫型材的振动速度，整体的振动速度依然稍低。1 000 Hz～2 000 Hz 之间两者的振动速度基本一致。在2 000 Hz～3 500 Hz 填充泡沫之后上面板的振动速度甚至超过了填充前的振动速度，这是由于填充泡沫之后结构与空气的耦合作用加大，更多的空气能量传递到上面板，这与图3辐射效率在3 000 Hz 以下明显增加的结果是一致的。3 500 Hz～4 000 Hz 范围内两者结构的振动速度基本一致。

3.3 填充泡沫对结构隔声量的影响

由公式（3）可知隔声量是由入射能量和透射能量共同决定，两次模型采用的输入声压级均为1 Pa，因此入射能量不变，透射能量可以近似地由公式4表示，因此隔声量的变化取决于前述的辐射效率和表面振动速度，即隔声量与振动速度和辐射效率成反比。图7(a)和图7(b)分别以对数和线性坐标的形式表示了仿真模型的隔声变化。从图7(a)可以看出在300 Hz以下，填充泡沫后结构的隔声量有明显的上升。分析其原因，从图3和图6可以看到300Hz以下结构的辐射效率虽然有所增加，但是辐射面振动速度下降的更为明显，这是隔声量上升的主要原因。

图6 有无填充泡沫上面板表面振动速度对比

图3 和图6 显示在300 Hz～1 000 Hz 之间填充泡沫的表面振动速度虽然依然略低于无泡沫结构的振动速度，然而填充泡沫的辐射效率要大于无泡沫结构，在振动速度下降和辐射效率增高的两种相反的作用下隔声量规律并不明显，如图7(a)所示。在1 000 Hz～3 500 Hz 之间，图3 和图6 显示填充泡沫前后表面的振动速度基本一致，而辐射效率却远大于无泡沫的辐射效率，在辐射效率增加的作用下，图7(b)显示有泡沫结构的隔声效果明显低于无泡沫结构。3 500 Hz以上辐射效率和表面振动速度有无泡沫均一致，因此其隔声量也基本重合。

图7 有无泡沫填充结构的隔声量变化

4 实验验证

为了验证前述的分析结果，在实验室中对型材填充泡沫的结构进行实验，实验参考GB/T 19889.3－2005标准进行。

测试环境为混响室-混响室测试，样件置于两室中间，声源室采用球声源激励，并布置麦克风在声源室和接受室分别采集声信号。隔声量表示为：

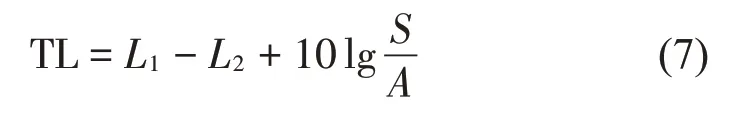
其中：L1，L2分别代表声源室和接受室的平均声压级，S为样件的面积，A为接受室的等效吸声量。

将仿真结果转换成1/3倍频程，并与实验结果进行对比如图8所示。可以看到实验与仿真结果对应一致，在250 Hz 以下填充泡沫隔声量明显上升；在250 Hz～1 000 Hz 与仿真结果类似，两种结构呈现交替变化；1 000 Hz 以上无填充泡沫结构的隔声量明显大于有泡沫结构。

图8 显示填充泡沫前后的计权隔声量Rw无论仿真还是实验均为30 dB，然而在频率上的表现形式却大为不同。填充泡沫之后隔声量在250 Hz 以下的低频有显著上升，而在1 000 Hz～3 500 Hz之间的隔声量却明显下降。因此在进行结构设计时不仅要看计权隔声量Rw 还需要针对噪声源情况和问题频率选择合适的设计。

图8 有无泡沫填充结构的隔声量测试和仿真结果对比

5 结语

本文通过混合模型对型材填充泡沫的声学性能影响进行了分析，对影响声学性能的两个关键因素—辐射效率和振动速度进行了详细解析，给出增加泡沫前后两者的变化和带来的隔声量的影响，最后对实验结果和仿真结果进行对比验证，最终得到如下结论：

(1)填充泡沫后，由于泡沫作用结构在250 Hz～3 500 Hz结构辐射效率明显增加。

(2)填充泡沫前，型材结构在200 Hz以下表现为整体模态，200 Hz以上由整体模态向局部模态转变；填充硬质泡沫后结构内部的耦合作用更大，使得结构由整体模态向局部模态的转变频率由200 Hz 提高至2 000 Hz。

(3)填充硬质泡沫使得400 Hz 以下结构表面振动速度明显下降；将仿真结果转换成1/3 倍频程，并与实验结果进行对比如图8所示。可以看到实验与仿真结果对应一致，在250 Hz以下填充泡沫隔声量明显上升；在250 Hz～1 000 Hz与仿真结果类似，两种结构呈现交替变化；1 000 Hz 以上无填充泡沫结构的隔声量明显大于有泡沫结构。1 000 Hz除部分峰值点的振动，填充泡沫结构表面振动速度依然稍低于无填充泡沫结构；在1 000 Hz～2 000 Hz 及3 500 Hz 以上填充泡沫前后表面振动速度基本一致；2 000 Hz～3 500 Hz填充泡沫之后的表面振动速度甚至超过了未填充泡沫的振动速度。

(4) 填充硬质泡沫前后计权隔声量Rw均为30 dB，但是隔声量的频率表现完全不同。填充硬质泡沫能够明显地增加250 Hz以下的结构隔声性能，但是降低了1 000 Hz～3 500 Hz频率之间的隔声量，因此进行声学设计时需要针对噪声源和问题频率进行设计。

(5)仿真模型与实验模型的结果和对应关系一致，说明通过仿真方法能够很好的预测泡沫填充对结构隔声效果的影响，同时结合模型的辐射效率和振动的分析能够更加深入地理解隔声量变化的机理。