高速铁路路基不均匀沉降对双块式无砟轨道动力特征影响研究
2021-10-22程年圣
程年圣
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
0 引 言
路基不均匀沉降导致高速铁路出现平顺性和稳定性问题,影响了列车运行的舒适性、安全性及轨道主体结构的服役性能,成为高速铁路建设和运营必须解决的难题。无砟轨道具有较高的保持几何形位的优势,随着高速铁路大规模的建设而逐步发展,已经成为高速铁路的主要轨道型式[1]。
国内外对高速铁路路基不均匀沉降开展了大量研究工作,Lundqvist等[2]分析了轨道几何状态恶化及轨枕空吊对轮轨动力作用的影响;蔡成标等[3]分析了路基沉降对系统动力响应的影响,基于舒适性指标提出了路基不均匀沉降控制限值;韩义涛等[4]分析了不同行车速度对应的路基沉降控制值;Banimahd等[5]分析了过渡段刚度不均对上部车辆轨道耦合系统的动态影响。
本文为研究高速铁路路基不均匀沉降对双块式无砟轨道影响动力特征,建立了车辆-双块式无砟轨道-路基不均匀沉降耦合动力模型,分别对路基不均匀沉降时双块式无砟轨道结构动态受力及振动特征进行分析,并分析了沉降波长、沉降幅值及行车速度的影响。
1 计算模型及参数
图1为车辆-双块式无砟轨道-路基沉降动力学耦合分析模型。无砟轨道模型方面,纵向连续式双块式无砟轨道长度为200 m,由道床板和支承层组成,道床板为C40现浇混凝土,支承层为HGT水硬性混凝土。扣件、道床板及支承层模型采用空间实体单元模拟无砟轨道,扣件模型采用三向弹簧-阻尼单元模拟,双块式无砟轨道模型基本参数见表1。车辆模型方面,采用我国高速铁路CRH380A统型动车组,定距为2.5 m,轴距为17 m,轴重为15 t。车辆由车体、转向架和轮对及两系悬挂构成,车体、转向架、轮对按刚体考虑。轮轨间法向作用力由赫兹接触理论确定,切向蠕滑力由蠕滑理论确定。

图1 车辆-轨道-路基沉降耦合模型
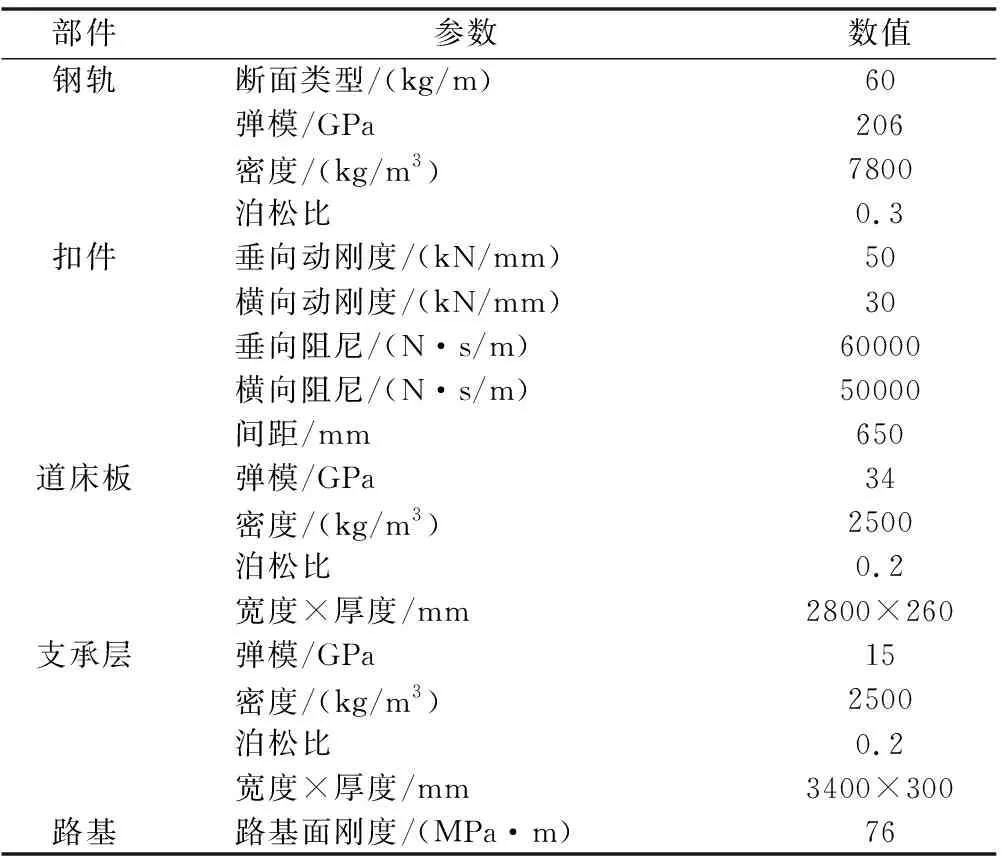
表1 双块式无砟轨道基本参数
2 路基不均匀沉降对轨道结构动态受力影响
2.1 路基不均匀沉降波长的影响
选取行车速度为350 km/h,沉降幅值为40 mm,沉降波长分别为5 m、10 m、20 m、30 m、60 m时,分析路基不均匀沉降波长对双块式无砟轨道结构动态受力的影响。
图2为不同沉降波长时道床板底部拉应力纵向分布,可以看出,在沉降发生位置处,道床板底部拉应力达到峰值,两端离缝位置处出现反弯现象。沉降波长较小时峰值现象明显,沉降波长为60 m时,拉应力峰值已不明显,说明沉降波长较大时,对道床板受力已影响较小。道床板底部纵向拉应力峰值随沉降波长变化,可以看出,随着波长增大,道床板底部拉应力呈减小趋势,沉降波长为10 m时道床板底部拉应力达到峰值,峰值为4.86 MPa。随着沉降波长的增加,到60 m时道床板底部拉应力仅为1.71 MPa。

图2 不同沉降波长时道床板底部拉应力纵向分布
图3为不同沉降波长时支承层底部拉应力纵向分布,可以看出,在沉降发生位置处,支承层底部拉应力达到峰值,两端离缝位置处出现反弯现象。沉降波长为5 m、10 m、20 m、30 m时峰值较为明显,沉降波长为60 m时,支承层底部受力较为均匀,无明显峰值。随着波长增大,支承层底部拉应力呈减小趋势,沉降波长为10 m时支承层底部拉应力达到峰值,峰值为2.48 MPa。沉降波长为60 m时支承层底部拉应力已降为0.57 MPa。

图3 不同沉降波长时支承层底部拉应力纵向分布
2.2 路基不均匀沉降幅值的影响
图4为不同沉降幅值时道床板底部拉应力纵向分布,可以看出,在沉降发生位置处,道床板底部拉应力达到峰值,两端离缝位置处出现反弯现象。幅值越大,峰值越明显。随着幅值增大,道床板底部拉应力呈增加趋势。沉降幅值20~80 mm范围内,道床板底部纵向拉应力变化范围为2.7~10.6 MPa,增加292.6%,增幅明显,可见沉降幅值对道床板底部纵向拉应力影响显著。
图4 不同沉降幅值时道床板底部拉应力纵向分布
图5为不同沉降幅值时支承层底部拉应力纵向分布,可以看出,在沉降发生位置处,支承层底部拉应力达到峰值,两端离缝位置处出现反弯现象。幅值越大,峰值越明显。随着幅值增大,支承层底部拉应力呈线性增大趋势。沉降幅值20~80 mm范围内,支承层底部纵向拉应力变化范围为1.2~5.3 MPa,增加341.7%,增幅明显,可见沉降幅值对支承层底部纵向拉应力影响显著。

图5 不同沉降幅值时支承层底部拉应力纵向分布
3 路基不均匀沉降对轨道结构振动特征影响分析
3.1 路基不均匀沉降波长的影响
选取行车速度为350 km/h,沉降幅值为40 mm,沉降波长分别为5 m、10 m、20 m、30 m、60 m时,分析路基不均匀沉降波长对双块式无砟轨道结构振动特征的影响。
图6为不同沉降波长时道床板垂向加速度纵向分布,可以看出,结构层离缝处,道床板的垂向加速度较大,沉降峰值位置处相对较小。

图6 不同沉降波长时道床板垂向加速度纵向分布
为便于分析路基不均匀沉降对双块式无砟轨道结构振动特征的影响,取路基不均匀沉降范围内,轨道结构的垂向加速度平均值进行分析。图7为道床板垂向加速度随沉降波长变化规律,可以看出,道床板垂向加速度随沉降波长的增加而减小。沉降波长范围为5~60 m,道床板垂向加速度平均值变化范围为530~320 m/s2,量值减少39.6%。

图7 道床板垂向加速度随沉降波长变化规律
图8为不同沉降波长时支承层垂向加速度纵向分布,可以看出,沉降波长为5 m、10 m短波长时,沉降发生处,支承层的垂向加速度较大。沉降波长大于10 m后,支承层垂向加速度较为均匀。

图8 不同沉降波长时支承层垂向加速度纵向分布
图9为支承层垂向加速度随沉降波长变化规律,可以看出,沉降波长对支承层垂向加速度平均值的影响较小,沉降波长范围为5~60 m,支承层垂向加速度平均值变化范围为28~31 m/s2,变化范围为10%左右。垂向加速度最大值方面,波长越短,支承层垂向加速度越大。
图9 支承层垂向加速度随沉降波长变化规律
3.2 路基不均匀沉降幅值的影响
选取行车速度为350 km/h,沉降波长为10 m,沉降幅值分别为20 mm、40 mm、60 mm、80 mm时,分析路基不均匀沉降幅值对双块式无砟轨道结构振动特征的影响。
图10为不同沉降幅值时道床板垂向加速度纵向分布,可以看出,结构层离缝处,道床板的垂向加速度较大,沉降峰值位置处相对较小。
图10 不同沉降幅值时道床板垂向加速度纵向分布
图11为道床板垂向加速度随沉降幅值变化规律,可以看出,道床板垂向加速度随沉降幅值的增加而增大。沉降幅值范围为20~80 mm,道床板垂向加速度平均值变化范围为467~508 m/s2,量值增加9%,增加量值不明显。

图11 道床板垂向加速度随沉降幅值变化规律
图12为不同沉降幅值时支承层垂向加速度纵向分布,可以看出,沉降发生处,支承层的垂向加速度较大。

图12 不同沉降幅值时支承层垂向加速度纵向分布
图13为支承层垂向加速度随沉降幅值变化规律,可以看出,沉降幅值对支承层垂向加速度平均值的影响较大,幅值越大,加速度越大。沉降幅值范围为20~80 mm,支承层垂向加速度平均值变化范围为26~65m/s2,量值增加150%,增加量值明显。

图13 支承层垂向加速度随沉降幅值变化规律
4 结 论
本文分析了路基不均匀沉降状态下双块式无砟轨道动力特征,包括轨道结构动态受力和振动特征影响分析,并讨论了沉降波长、沉降幅值的影响。得出主要结论如下:
(1)路基中短波长不均匀沉降对双块式无砟轨道结构受力影响较大,轨道结构受力随着沉降波长的增加而逐渐减小。路基不均匀沉降波长应控制在20 m以上。
(2)随着路基不均匀幅值的增加,轨道结构受力显著增大,应重点控制不均匀沉降幅值的增长。
(3)路基不均匀沉降波长主要影响道床板的垂向加速度,随波长的增加而减小,对支承层垂向加速度的影响较小。
(4)不均匀沉降幅值主要影响支承层垂向加速度,随沉降幅值的增加而增大,对道床板垂向加速度的影响较小。
