附着滴在粗糙多孔介质表面铺展渗透的数值研究

2021-10-22邓辉良李培超

轻工机械 2021年5期

邓辉良，李培超

(上海工程技术大学机械与汽车工程学院，上海 201620)

润湿现象在日常生活和工业中都很普遍，在这些现象中，液滴在多孔介质上的铺展和渗透对于实际应用有着至关重要的作用。例如农药喷洒、喷墨打印、电解质流动、强化采油和火灾的扑救及内燃机喷油嘴的喷射等都会有液滴和壁面间的相互作用[1-5]。当液滴在多孔基板表面扩散时，液相动力学产生于多孔介质内部毛细渗透与表面接触线运动之间的复杂耦合。

1992年，Chandra等[6]对液滴撞击多孔陶瓷壁面后，液滴的变形和扩散进行了摄影记录。研究发现，在液滴撞击的初始阶段，在多孔和不锈钢表面上的液滴铺展面积和铺展速度的变化与温度无关，分析表明这一结果归因于可忽略的表面张力和粘滞效应。Starov等[7]通过实验研究了小硅油滴在各种干厚多孔衬底上的扩散行为，他们观测了多孔表面液滴半径和润湿区半径的时间演变。Leang等[8]利用高速成像技术对多孔层自吸的动力学和力学特性进行了实验研究，研究证明了溶剂渗透是造成系统中粘性组分出现的原因。由于实验受到设备、环境和人为因素的影响，且当液滴撞击速度很大时无法清楚地观察液滴铺展和渗透的具体状况，而数值模拟刚好可以弥补实验研究的不足；数值模拟不仅可以给出多孔介质外液滴的演化过程，而且可以描述多孔介质内的流体流动。Espin等[9]以润滑理论模型为框架，推导出液滴在考虑多孔基底表面粗糙度时的扩散和吸收的数学模型，并进行了数值模拟，研究了渗透率和粗糙度对轴对称液滴扩展的影响。Yang等[10]通过在管壁上装饰微槽，研究了表面粗糙度对液体铺展中润湿接触线的影响。Reis等[11-12]通过求解多孔介质内外流体流动的质量和动量守恒方程，对液滴冲击多孔介质的动力学行为进行了数值研究。Fu等[13]利用流体体积(VOF)法来精确地跟踪液滴的变形，并结合压力隐式分裂算子(PISO)算法，详细研究了液滴特性、多孔介质特性和液体与多孔介质润湿性对附着滴铺展和渗透的影响。

上述实验工作和数值模拟为描述和理解液滴在多孔介质表面的动力学行为提供了重要的信息。课题组基于Fu等[13]2918-2919研究的基础上，对多孔介质模型进行了优化。分析了液滴邦德数、平衡接触角、达西数以及多孔介质表面粗糙度对铺展和渗透的影响，旨在更真实地认识附着滴在多孔介质表面的铺展渗透问题。

1 数学模型

1.1 问题描述

多孔介质由于孔隙、颗粒介质以及制备或加工等因数的存在，表面必定呈现凹凸不平的现象，且粗糙度在很大程度上影响液滴在多孔介质铺展渗透[14]。其中关于表面粗糙度的研究中，很多研究者用凹凸槽来建立表面粗糙度模型[15-16]，基于前人对粗糙度的研究，我们在Fu等研究的基础上，在多孔介质表面增加凹凸槽来代表表面粗糙度并建立模型。

1.2 模型建立

液滴撞击多孔基底的表面，可以简化为图1(a)所示的轴对称形式，其中x和y分别是径向和纵向轴坐标，其中虚线区域为计算区域。x轴是空气与多孔介质层的交界面，x轴上方为空气介质，下方为多孔介质；假设液滴为球形，图1(b)为液滴变形示意图，其铺展半径为R，渗透深度为H；图1(c)为液滴铺展渗透的局部放大，其中凸台宽度a，凹槽宽度b，高度c。

图1 液滴物理模型Figure 1 Droplet physical model

2 模型验证

图与时间T*的关系Figure 2 Relationship between and T*

上述数值算例验证结果表明，文中所建立的模型可以模拟微滴撞击多孔介质表面的运动过程，并且与前人的实验结果吻合得很好。下面，我们将基于文中建立的数学模型，对附着液滴在多孔介质表面的动力学行为开展参数研究。

3 参数分析

课题组主要研究液滴韦伯数、平衡接触角、达西数以及多孔介质表面粗糙度对液滴动力学行为的影响。一些物理参数对液滴动力学的影响可以用量纲为一的参数来描述，包括邦德数(Bo)和达西数(Da)。

邦德数表示流体重力和表面张力之比，其表达式为

(1)

式中：ρ是液滴密度，g是重力加速度，r0是液滴初始半径，σ为表面张力。

达西数表示多孔介质的渗透性，其表达式为

(2)

式中K为多孔介质的渗率。

计算中使用的微液滴为水，初始参数如下：

初始半径r0=1 mm，重力加速度g=9.81 m/s2，速度u0=0，气液界面张力σ=72.8×10-3N/m,平衡接触角θ=60°，孔隙度φ=0.55，多孔介质颗粒直径dp=0.1 mm，a=b=c=20 μm。

3.1 邦德数的影响

邦德数的值表示重力对表面张力的重要性。根据式(1)，当r0一定时，加速度越大，邦德数越大。图3为邦德数Bo分别为0.137，0.685和1.370时附着滴铺展半径和渗透深度随时间的变化曲线。由图3可知，随着邦德数的增加，重力起主导作用就越明显，液滴的铺展和渗透都增强，单位时间内有更多的液体进入到多孔介质内部。Bell等[17]3860研究了重力对不渗透粗糙壁面上液滴形态的影响，他们发现重力的影响是双重的。即在相同尺寸的液滴下，有较大邦德数的液滴会更快铺展，由于重力的压扁作用会增大液滴与壁面的接触半径，减小液滴高度；另一方面，邦德数较大时，停留在不渗透凹凸槽的液体更多，使液滴没有足够的液体铺展。很显然，Bell等的研究结果与我们的数值结果一致，上述现象也解释了铺展和渗透有很强的竞争关系。

图3 不同邦德数下液滴铺展半径和渗透深度随时间的变化Figure 3 Changes in droplet spreading radius and penetration depth with time under different Bond numbers

3.2 平衡接触角的影响

图4为液滴在不同平衡接触角下随时间的演变。从图中可以看出，当平衡接触角θeq为30°和60°时，多孔介质壁面为亲水壁面，液滴铺展半径和渗透深度都较大，而θeq为30°的壁面液滴铺展更大；这是因为接触角越小，润湿性越好，有利于液滴在多孔介质表面铺展。当平衡接触角θeq为120°时，铺展半径明显比前两者小，而后期随着时间的推移，渗透深度在重力的作用下会增加。所以平衡接触角越大，衬底的润湿性越差，渗透作用越差，铺展半径越小。

图4 不同平衡接触角下液滴形状随时间演化Figure 4 Evolution of droplet shape with time under different equilibrium contact angles

3.3 达西数的影响

根据式(2)，当液滴r0一定时，达西数越大，多孔介质的渗透率越大。随着达西数值的增加，多孔衬底对液滴的阻力降低，渗透率增加。因此，随着达西数的增加，液滴更容易被多孔介质吸收。

图5为达西数值分别为5.5×10-4，5.5×10-5和5.5×10-7时的液滴铺展半径和渗透深度随时间变化曲线。由图中可以看出，在达西数值较小的情况下多孔介质对液滴的阻力更大，使液体渗透深度小得多，因此有更多的液体进行横向铺展。而达西数5.5×10-4时，液滴的抗渗透能力非常弱，以至于液滴在很短时间被多孔介质完全吸收。

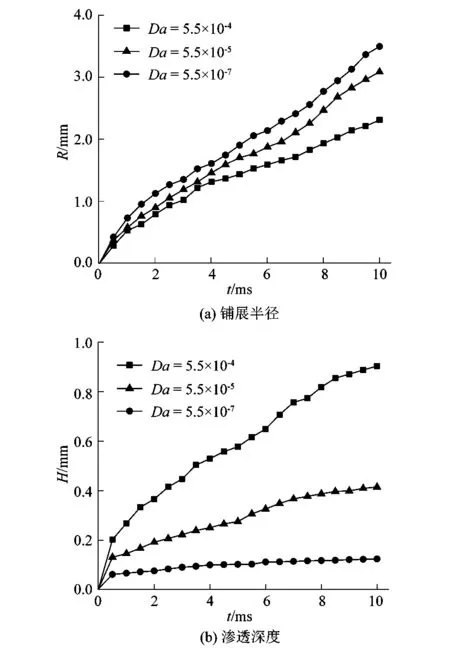
图5 不同达西数下铺展半径和渗透深度的变化Figure 5 Variations of spreading radius and penetration depth under different Darcy numbers

3.4 微结构表面粗糙度的影响

表1为3种多孔介质表面的沟槽结构参数。图6表示液滴在不同粗糙度多孔介质微结构表面形态随时间的变化。根据王宝和等[18]26的研究，凸台高度c越大，对应的粗糙度越大。结合图7(a)可知，由于粗糙度的存在，液滴铺展过程中会有能量损耗，且粗糙度越大，动能损耗越大，铺展半径越小。显然，这与王宝和等研究液滴在粗糙不渗透表面铺展的结果一致。由图7(b)可知，随着粗糙度的增大，液滴铺展越慢，单位时间内渗透到多孔介质内的液体越多。所以在竖直方向上，渗透深度随粗糙度的增大而增大。