纯铜研磨表面残余应力在液动压悬浮抛光中的松弛规律
2021-10-22应一帜
姜 涛, 谢 重,2, 应一帜
(1.台州职业技术学院 机电工程学院, 浙江 台州 318000;2.浙江工业大学 机械工程学院, 浙江 杭州 310014)
基于现有技术制备出的纳米薄膜在微电路、光学系统和生物学等领域得到了广泛的应用,具有良好的电磁、光学和力学等特性。纳米薄膜的制备要以原子级超光滑表面作为生长表面,且该生长表面的表面质量对薄膜的制备起着决定性的作用,特别是生长表面上的残余应力的分布对薄膜的生长质量影响非常大。所以,如何改善超光滑纳米薄膜生长表面的残余应力的分布状态具有重要意义[1-2]。
液动压悬浮抛光是一种非接触式的超精密抛光方法,不仅能有效改善铜质工件表面粗糙度和位错形态,而且抛光过程中对工件表层残余应力的改善有着积极作用。国内外很多学者采用不同的工艺研究了不同金属材料表面残余应力的松弛规律,其中,胡永会等[3-4]对7075高强铝合金进行喷砂强化,采用XRD研究喷砂表面在循环载荷作用下残余应力的松弛规律。王建明等[5]研究了7075铝合金在疲劳载荷循环次数、应力比、初始残余应力场等因素下对喷丸表面残余应力的松弛规律。高玉魁[6]采用XRD研究了超高强度钢在旋转弯曲疲劳过程中喷丸表面残余应力的松弛规律。Mauduit等[7]对TRIP780高强度钢进行喷丸强化,采用XRD研究循环载荷下喷丸表面残余应力的松弛规律。ISA等[8]对A516 Gr70钢进行喷丸强化,采用XRD研究循环载荷下喷丸表面残余应力的松弛规律,发现随着喷丸强化的载荷增大,循环载荷下的应力松弛效果更好。液动压悬浮抛光方法作为一种超光滑工件表面的应力松弛手段,对机械研磨后的纯铜表面应力松弛起到积极作用。
目前,对纯铜表面的应力松弛效应的相关研究相对较少,课题组基于ABAQUS软件建立了液动压悬浮抛光过程的有限元数值模型,模拟单/多颗磨粒连续撞击铜质工件表面,研究磨粒运动参数对铜质工件表面的残余应力松弛规律的影响。先选取传统研抛的工件和传统研抛后再液动压悬浮抛光的工件,再使用XRD分别测试工件表层的残余应力,结果显示液动压悬浮抛光对改善铜质工件表层残余应力状态有良好的效果,验证了数值模拟的准确性。最终,获得液动压悬浮抛光加工过程中工件表面的应力松弛状况,为进一步改善液动压悬浮抛光加工工艺提供参考。
1 单/多颗磨粒撞击的有限元模拟
1.1 有限元模型建立
使用有限元软件ABAQUS建立单/多颗磨粒连续撞击工件表面的三维数值模型,工件尺寸为10 mm×10 mm×1 mm。数值模型仿真时,为提高运算速度,提取的模型尺寸为30 μm×30 μm×6 μm,磨粒直径为7 μm。液动压悬浮抛光的铜质工件需要先进行机械研磨粗加工,机械研磨抛光后铜质工件表面的粗糙度Ra约为50 nm,所以在建立三维模型时通过起伏的轮廓表面来描述工件表面的粗糙度,起伏高度为50 nm,如图1所示。铜质工件的材料力学性能如表1所示。

图1 单颗磨粒撞击工件的有限元模型Figure 1 FEM of a single abrasive particle impacting workpiece

表1 铜质工件材料的力学性能Table 1 Mechanical properties of copper workpiece
液动压悬浮抛光中磨粒与工件的撞击近似水平,取θ=0.03°[8-10],通过该撞击角度换算出不同加工转速n下磨粒与工件表面撞击的分向速度,如表2所示。其中V是磨粒撞击时在工件平面内的合速度,VZ是磨粒撞击时在Z方向的分速度。

表2 不同转速下磨粒对应的VX和VZ值Table 2 Corresponding VX and VZ values of abrasive particles at different speeds
1.2 网格划分及初始条件
铜质工件的网格划分采用的是结构化网格,网格单元类型是Hex型,网格单元数量是90 000个。磨粒模拟成刚性球体,其网格划分采用的是非结构化网格,网格单元类型是Tet型,网格单元数量是16 852个,铜质工件底面使用旋转约束和位移约束。
对液动压悬浮抛光加工过程进行数值模拟时,不仅考虑机械研磨在铜质工件表面产生的粗糙度,同时要考虑机械研磨在工件表层形成的残余应力的分布状况。结合金明骏等[11]对传统机械研磨抛光加工后工件表面残余应力分布的研究,以及后文中残余应力的测试结果和残余应力深度的计算结果,类比出研抛后铜质工件表面在一定厚度内的残余应力分布,如图2所示。利用ABAQUS中施加初始应力的用户子程序SIGINI,将该应力作为初始应力施加到工件模型中,如图3所示;为提高运算速度,假设磨粒从近壁面位置开始撞击铜质工件表面。

图2 不同深度内X方向的初始残余应力Figure 2 Initial residual stress in X direction at different depths
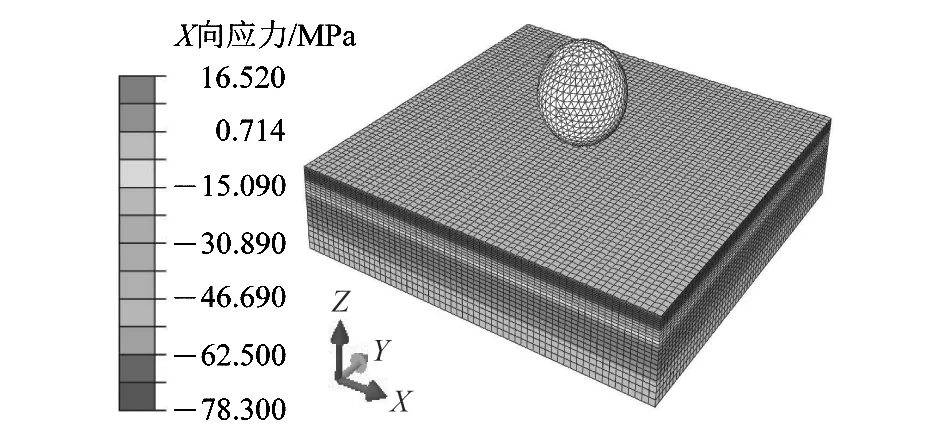
图3 施加预应力后的有限元模型Figure 3 FEM of applying prestress
1.3 有限元计算结果
1.3.1 单颗磨粒撞击
数值模拟3种抛光转速下单颗磨粒对铜质工件表面的连续撞击,从而改善工件表层的应力状态。如图4所示的截面应力云图,是单颗磨粒对工件同一位置连续撞击达到10次后的效果图。
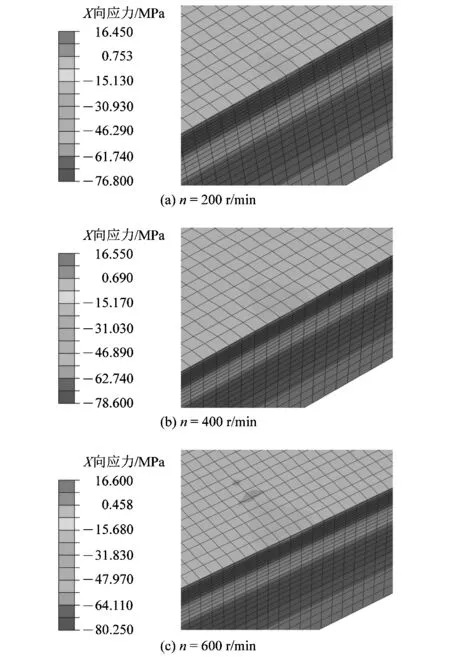
图4 单颗磨粒撞击工件的截面应力云图Figure 4 Cross-sectional stress diagram of a single abrasive particle impacting workpiece
单颗磨粒连续撞击铜质工件表面后,极大地减小了撞击点工件表层的压应力,随着转速的增加工件表层的压应力减小的效果越明显。同时,从截面应力云图可以看出,磨粒撞击后对工件表面的内部的应力影响很小。所以,液动压悬浮抛光在工件表层具备实现微量切削的条件,从而能获得低应力的超光滑表面。图5所示为抛光转速600 r/min下工件不同厚度内的应力分布。

图5 600 r/min转速下工件不同厚度内的应力分布Figure 5 Stress distribution in the depth of workpiece at 600 r/min
图6所示为不同转速下单磨粒连续撞击的铜质工件表面的应力松弛曲线。从图中可清晰看出,在单颗磨粒连续撞击次数达到10次左右时,工件表面撞击点位置的残余压应力不再减小而达到一个稳定值,转速越高该稳定值的绝对值越小,即工件表层的压应力减小的效果越明显。同时,前几次的磨粒撞击对撞击点的残余压应力变化很大,特别是首次撞击的影响最大。

图6 单颗磨粒撞击工件的应力松弛曲线Figure 6 Stress relaxation curve of a single abrasive particle impacting workpiece
1.3.2 多颗磨粒撞击
磨粒流在液动压悬浮抛光流场中以近似水平的角度有序地撞击工件表面,通过研究磨粒流与工件表面撞击形成的应力改善区的应力变化来描述铜质工件表面在液动压悬浮抛光中的应力松弛规律。图7所示为多颗磨粒撞击的有限元模型,以行距和列距都为0.001 mm向X方向和Y方向各阵列4个,共16颗磨粒,其他所有参数与单颗磨粒的撞击模型相同。

图7 多颗磨粒撞击工件的有限元模型Figure 7 FEM of multiple abrasive particles impacting workpiece
对多颗磨粒撞击进行数值模拟后,获得如图8所示的铜质工件表面的应力云图。多颗磨粒连续撞击工件表面形成的应力影响区随着抛光转速的增加而增大,磨粒撞击的应力影响区域的应力值趋于均匀化,但随着转速的提高撞击区域的边界位置的应力波动较大。选取应力云图中间均匀区域的深色方框内的16个单元作为应力分析对象,在每次撞击结束后,ABAQUS会输出该16个网格单元上的应力值并且求应力平均值,由此得到多颗磨粒在连续撞击过程中工件表面的应力松弛曲线,如图9所示。该应力松弛过程基本与单颗磨粒撞击情况一致,但松弛效果要比单颗磨粒撞击的更明显,因此多颗磨粒撞击能更完整地反映抛光加工过程中的应力松弛过程。
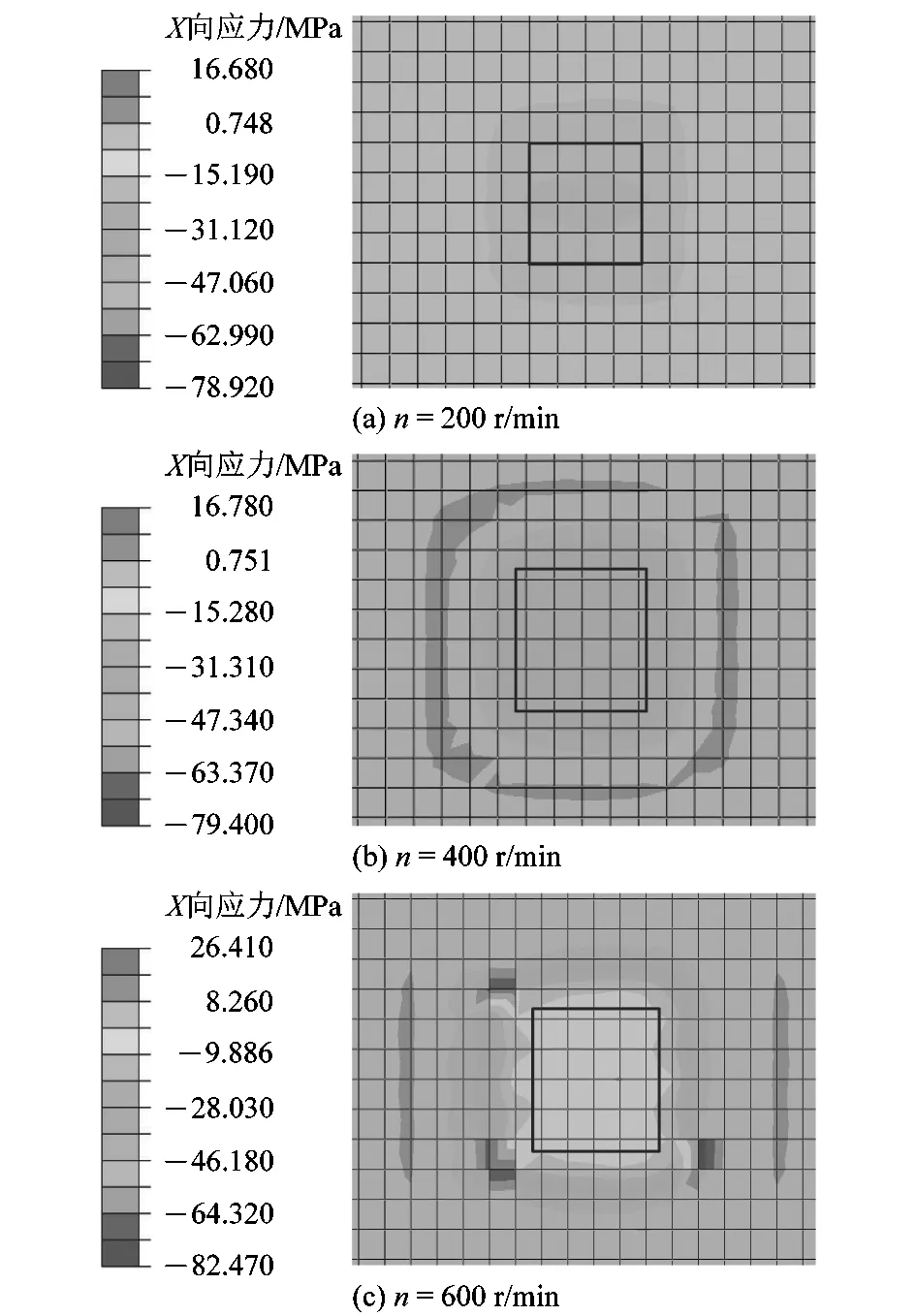
图8 多颗磨粒撞击工件的应力云图Figure 8 Stress diagram of multiple abrasive particles impacting workpiece
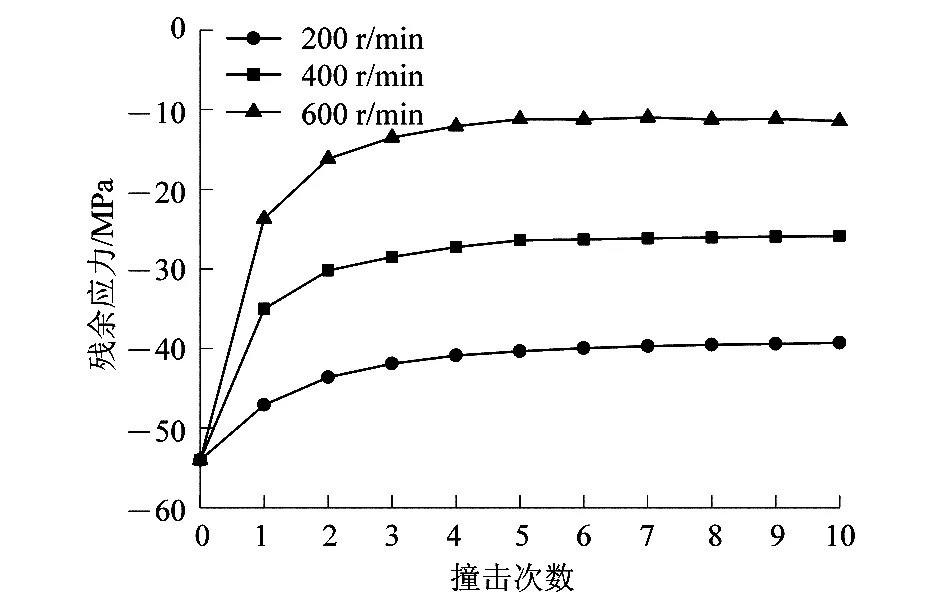
图9 多可磨粒撞击工件的应力松弛曲线Figure 9 Stress relaxation curve of multiple abrasive particles impacting workpiece
2 工件表面残余应力测试
2.1 测试准备
该测试实验设备是LXRD大功率X射线应力仪,X射线方位角的范围是±45°,选用铜靶Cu K-Alpha,波长λ=0.154 2 nm,采用同倾固定ψ法。
选取的试样尺寸为10 mm×10 mm×1 mm,试样Ⅰ、Ⅱ为传统研抛的工件,试样Ⅲ、Ⅳ为传统研抛后再液动压悬浮抛光的工件,分别对4个试样表面的X,Y方向的表面应力进行测试。如图10所示,定义了铜质工件初始的X方向和Y方向,其中残余应力测试点D在工件表面的中心位置。

图10 铜质工件的X和Y方向Figure 10 X and Y direction of copper workpiece
2.2 测试结果分析
2.2.1 X射线透射深度分析
X射线的透射深度一般为数十微米以内,在透射深度内,工件表面的应力随厚度的变化而改变,这是一种二维的表层应力分布状态,工件表面垂直方向上的应力为零[12]。X射线的透射深度公式为
(1)
式中:ψ为衍射晶面方位角,θψX为该方位角对应的衍射角的一半,μm是质量衰减系数,ρ是被测材料密度,I0为入射线强度,I为衍射线强度,取I0/I=e。
由于Cu K-Alpha的能量为8.04 keV,根据张帅等[13]的Cu质量衰减系数曲线分布,可查得μm≈90 cm2·g-1。同时,铜质工件的衍射角2θψX=144.68°,ρ=8.98 g/cm3,因此可计算出Cu K-Alpha射线在不同方位角下的透射深度,如表3所示。

表3 不同方位角下的透射深度Table 3 Transmission depth at different azimuth angles
可以看出,X射线在不同方位角下的透射深度不同,为本文前面数值模拟中的工件表面的应力层深度提供参考值。X射线测量应力一般是用特性X射线穿透深度相应的一种加权平均值来评定材料表面的应力,由此,本文前面的数值模拟中的工件应力层深度取值为6 μm。
2.2.2 工件表面应力分析
如图11所示为XRD测试获得的2θψX-sin2ψ拟合曲线,一个点测试过程中会有2个测量值,该2个测量值为图中2条直线的斜率。可以通过2条直线的靠近程度来判断该点测得的残余应力值是否准确,2条直线距离靠得越近则测得的残余应力值越准确。图11中显示的残余应力值分别为-64.9±10.3 MPa和-23.4±13.9 MPa,因此液动压悬浮抛光加工对铜质工件表面的残余应力具有比较良好的松弛效果。

图11 2种加工方式下的残余应力Figure 11 Residual stress under two processing methods
4个试样沿X,Y方向测得的残余应力值结果如表4所示。显然,试样Ⅰ和试样Ⅱ沿X,Y方向的残余应力值大小接近,符合传统研抛加工对工件表面应力状态的影响方式;试样Ⅲ和试样Ⅳ对工件表面X,Y方向的应力值有差别,说明液动压悬浮抛光对X,Y方向的应力松弛效果不尽相同。另一方面,通过测得传统研抛加工后的工件表面残余应力值,为本文前面数值模拟中的工件表面提供初始应力分布状态,从而能够更加真实地模拟出液动压悬浮抛光加工对工件表面的应力松弛规律。

表4 工件试样的残余应力值Table 4 Residual stress value of workpiece sample
3 结语
课题组采用有限元法建立液动压悬浮抛光过程中单/多颗磨粒连续撞击工件的数值模型,在模型中引入了传统研抛加工后的工件表面粗糙度和残余应力参数值,分析单/多颗磨粒连续撞击过程中铜质工件表面残余应力松弛状况,得到了以下结论:
1) 多颗磨粒撞击的模型更能全面地反映液动压悬浮抛光过程中的应力松弛效应,工件表面的应力松弛效果随着抛光转速增加而提高,且随着磨粒连续撞击的次数增加铜质工件表面的应力会减小到一个稳定值,前几次的磨粒撞击对撞击点的残余压应力变化很大,特别是首次撞击的影响最大。
2) 液动压悬浮抛光加工的工件应力层影响深度小,对工件表面的应力松弛明显,对工件内部的应力松弛影响较小,抛光工件应力松弛后工件表面压应力趋于均匀化。
3) 液动压悬浮抛光流场中磨粒与铜质工件的撞击角度微小且受转速和抛光液浓度的影响小,在加入预应力的仿真模型中,以接近水平方向的力撞击工件对铜质工件表面的应力松弛效果有良好的稳定性,同时,也避免了大角度的磨粒撞击增大工件表面压应力的情况出现。
