隧道围岩中注浆锚杆的应力分布及影响因素研究

赵立财

(1.中铁十九局集团第三工程有限公司，辽宁 沈阳 110136；2.台湾科技大学 营建工程系，台湾 台北 10607)

隧道开挖过程中，岩土体中结构发生变化，原有应力平衡状态遭到破坏，当新应力场中压应力超过岩土体承压强度，开挖硐室周围产生塑性变形区[1-2]。隧道围岩压力过大还会产生大变形、岩爆等灾害。隧道支护中，注浆锚杆使用广泛，具有显著的经济和社会效应[3-4]。目前对于注浆锚杆的应用推广已有大量研究成果，但多是采用经验法和半经验法，尤其是设计过程中未弄清注浆锚杆的锚固机理[5-6]。由此，本文将注浆锚杆与周围浆体视作锚固体，分析锚固体受力特征，推导锚固体轴应力和剪应力表达式，通过理论分析和数值模拟对比证明本文理论解析的合理性，并分析不同影响因素下锚固体应力分布的变化规律。研究成果为注浆锚杆应力分布规律研究及隧道支护提供一定参考。

1 锚固体应力分布理论解析

隧道施工过程中，锚杆注浆周围形成浆体，可近似看成锚杆外边缘裹了一层混凝土，则可将锚杆与浆体组成复合加固体，即成为“锚固体”。由于锚杆为中空锚杆，故锚固体的材料由锚杆内部浆体、锚杆及锚杆外围覆盖浆体组成，锚固体受力特征图如图1所示，“锚固体界面”表示灌浆材料与岩石之间的界面。

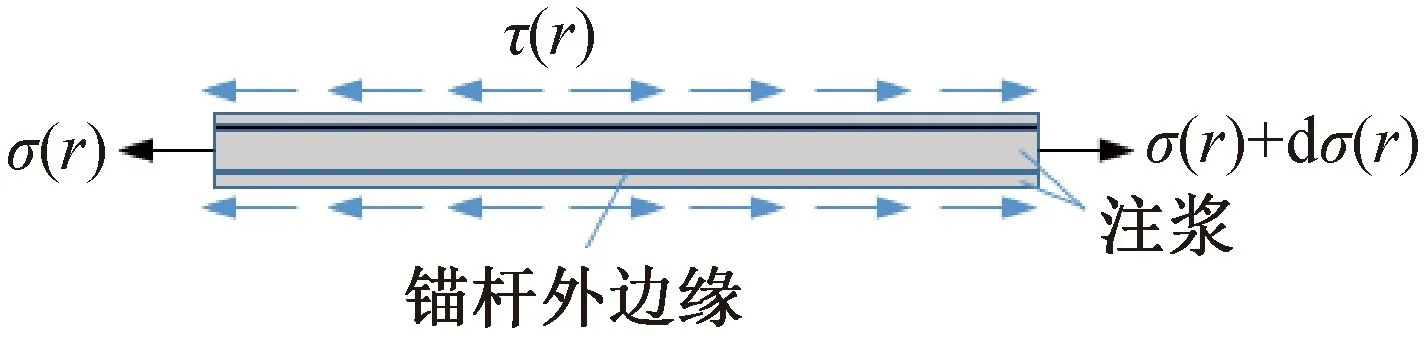
图1 锚固体受力特征图Fig.1 Stress characteristic diagram of anchor

根据锚固体的结构特点，令锚固体的等效弹性模量Ee为

(1)

式中：Ea、Eb分别为锚杆和浆体的弹性模量；Aa、Ab、Ac分别为锚杆内部、锚杆外部覆盖层以及锚杆的横截面积。

根据图1中锚固体受力特征，锚固体单元受力平衡条件有

Adσ(r)=q(r)Ddr

(2)

式中：σ(r)为锚固体单元轴应力，q(r)为锚固体单位长度摩阻力，A、D分别为锚固体的截面面积与周长，r为锚固体任意点到硐室中心距离。

锚固体的本构公式有[7]

(3)

式中：u(r)为锚固体轴线上的径向位移，Ee为锚固体等效弹性模量。

将式(3)代入式(2)可得

(4)

式中：Ae为锚固体等效横截面积。

以锚固体任意微元段为研究对象，某段所受摩阻力与该段杆体及其周围岩体之间的相对位移呈正比，则有

q(r)=Kt[u(r)-u(m)]

(5)

式中：Kt为锚固体剪切刚度，m代表锚固体中性点，u(m)为锚固体中性点的径向位移。

将式(5)代入式(4)可得

(6)

锚固体任意界面上轴向拉力有

N(r)=Aσ(r)

(7)

式中：N(r)为锚固体任意界面上轴向拉力。

联立式(2)、(6)和(7)有

(8)

由岩体力学理论[8]可知，任意锚固体界面周围岩体的径向位移为

(9)

式中：Rp为塑性区半径，p0和pc分别为地应力和支护应力，c和φ分别为围岩的内聚力和内摩擦角，μ为围岩泊松比，E为围岩弹性模量。

由式(9)可看出，围岩径向变形沿深度呈非线性变化，且硐壁围岩变形量最大。将式(9)代入式(8)求解可得

(10)

式中：rm为锚固体中性点到硐室中心距离，b为常数。

锚固体一般在洞壁添加垫板、螺栓固定，即施加预紧力F1，则边界容许范围为

P(r)|r=r0=F1/Ae

(11)

式中：r0为硐室半径。

将式(11)代入式(10)可得

(12)

再联立式(5)和式(9)可得摩阻力

(13)

锚固体内力图如图2所示，图中τ(r)和σ(r)为剪应力和轴应力，虚线表示中性点。

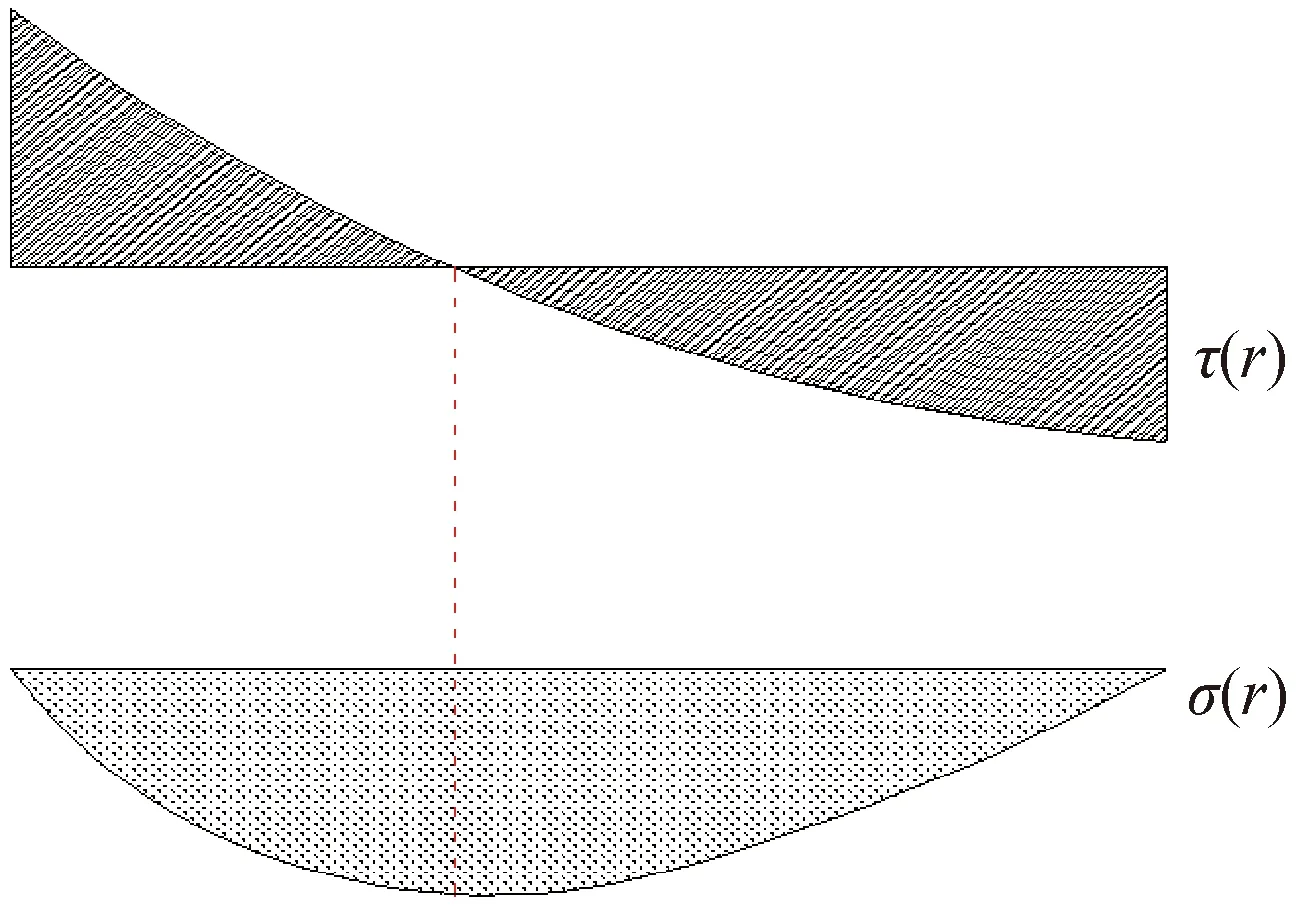
图2 锚固体内力图[9]Fig.2 Internal force diagram of anchor[9]

由图2可知，锚固体中性点处轴应力连续，则中性点两侧微小单元轴应力相等，于是有

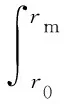
(14)

式中：L为锚杆长度。

联立式(9)、(13)和(14)可得锚固体中性点到硐室中心距离rm为

(15)

再结合式(10)和(15)可得轴应力表达式

(16)

式中：B为待定系数。

锚固体在中性点处轴应力达到最大值，于是有

(17)

一般地，锚固体剪应力计算公式如下[10]

(18)

式中：τ(r)为剪应力，ds为锚固体直径。

再将式(13)代入式(18)可得本文锚固体剪应力为

(19)

式(16)和(19)分别为本文锚固体轴应力和剪应力表达式。

2 注浆锚杆锚固体应力分析

2.1 模型建立

本文研究背景为沈阳至白河高铁工程新宾隧道，隧道进口里程为DK123+425，出口里程为DK133+600，中心里程为DK128+512.5，全长10 175 m。依据新建沈阳至白河高铁工程新宾隧道工程地质勘察报告，选取新宾隧道IV级围岩作为分析对象，IV级弱风化砂岩为全断面开挖方式，具体力学参数如表1所列。采用ABAQUS有限元软件对深埋隧道施工过程进行三维模拟，以隧道断面为原型，同时为了减小应力边界的影响，上下左右边界选取三倍以上的隧道跨度，模型尺寸(长×宽×高)为100 m×45 m×100 m，将模型左、右、下设置固定约束，上边界为自由面。采用的基本塑性准则为M-C准则，单元类型为C3D8，网格先布置全局种子再布置局部种子，沿边界向洞心由疏变密，网格以四边形为主，三维仿真模型如图3所示。

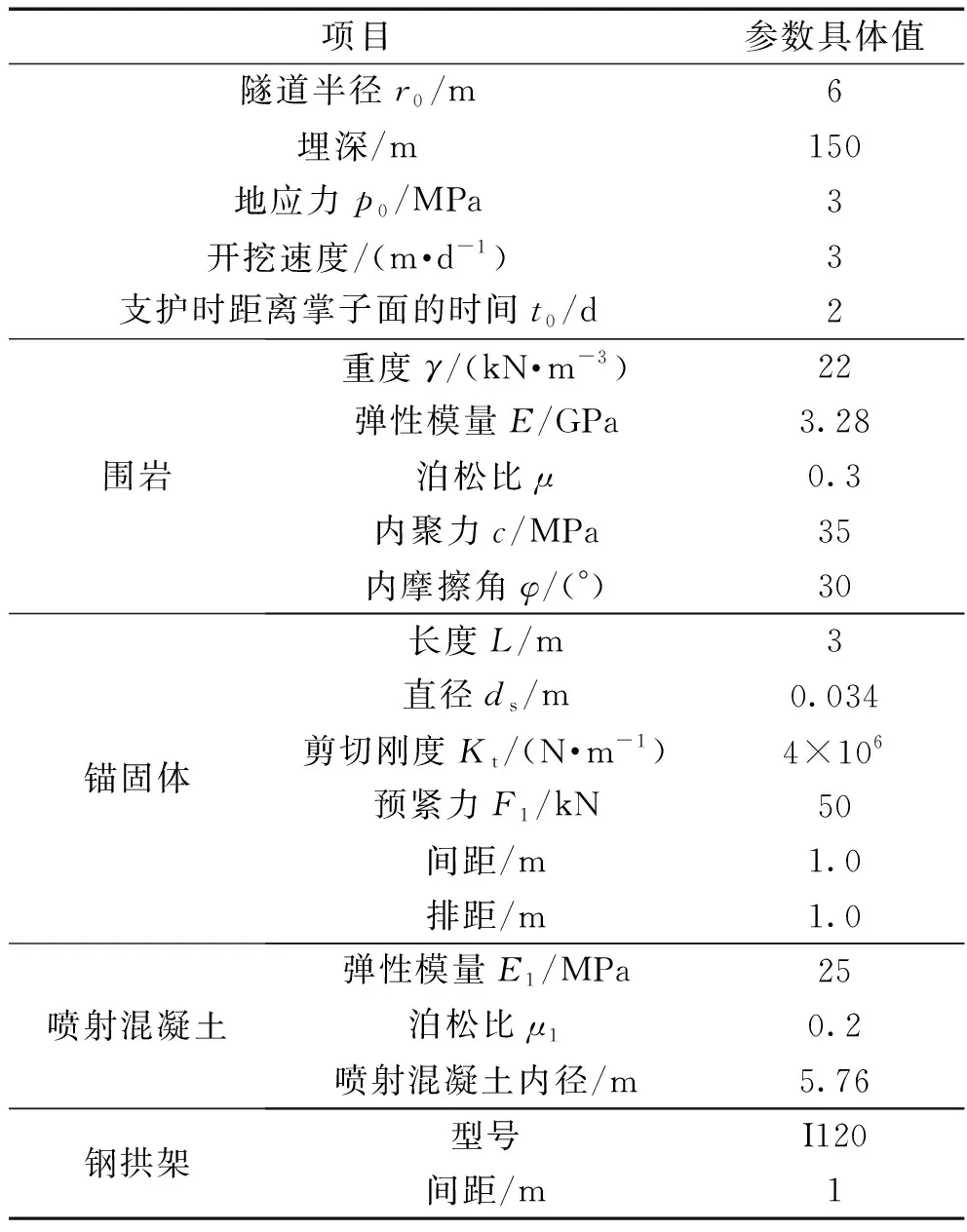
表1 隧道力学参数取值表

图3 隧道三维模型Fig.3 Three dimensional model of tunnel

2.2 模型计算

隧道开挖后的应力云图如图4所示。

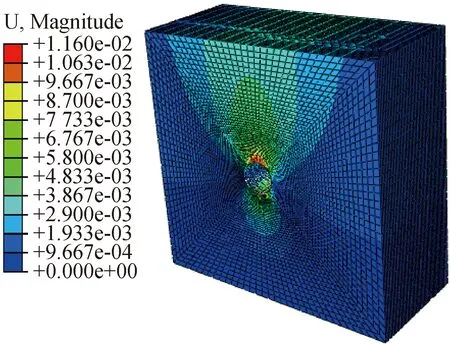
图4 隧道开挖后位移云图Fig.4 Displacement nephogram after tunnel excavation

由图4可看出，隧道开挖后拱顶变形最大，故以拱顶位置分析锚固体应力分布，取隧道模型中间位置断面为监测断面，并将数值模拟方法得到的锚固体应力与理论分析进行对比，以验证理论方法的可行性，分别得到锚固体的轴应力和剪应力的数值模拟和理论分析对比结果，如图5所示。

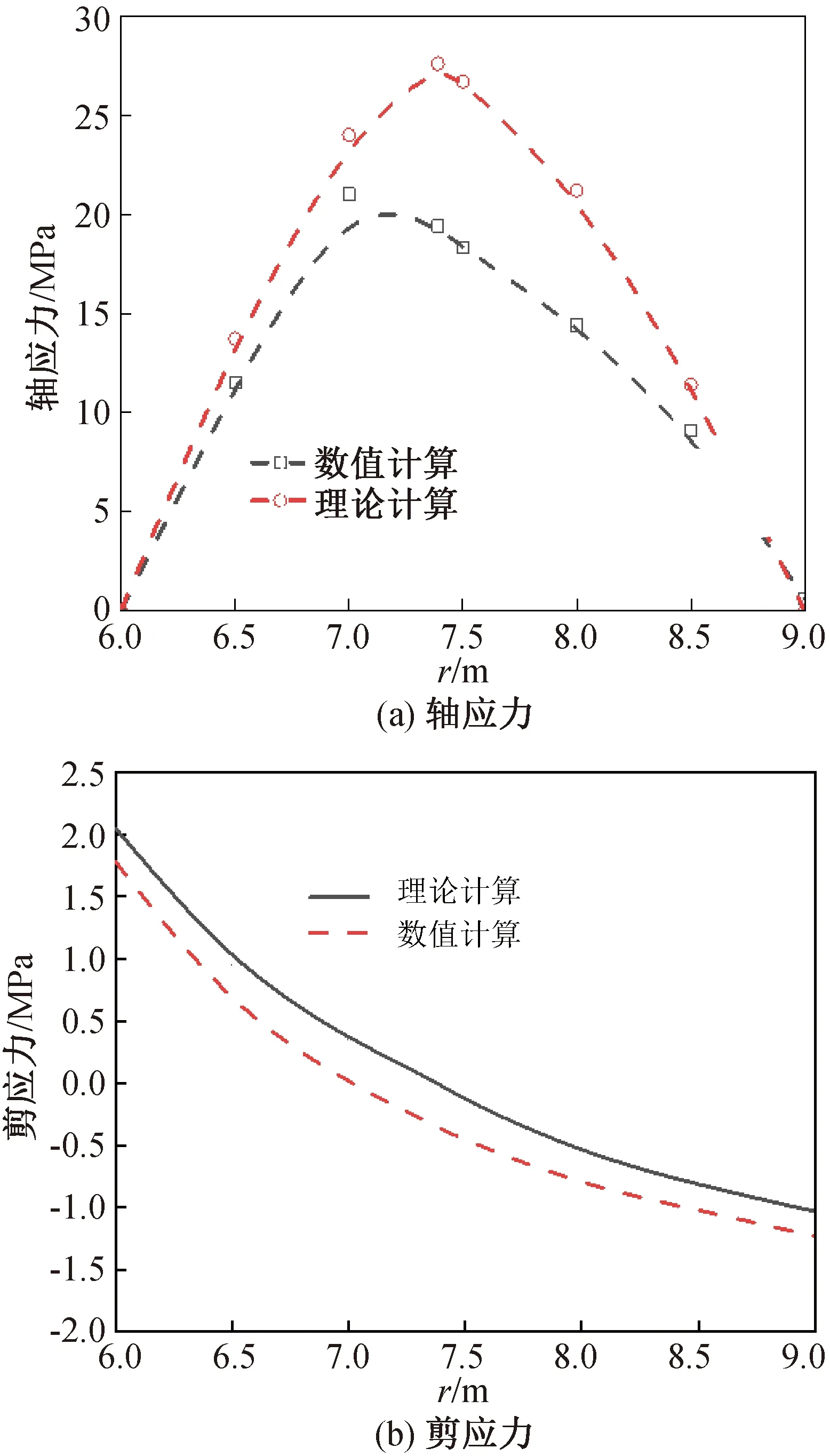
图5 锚固体应力分布曲线Fig.5 Stress distribution curves of anchor solid

由图5(a)可看出，理论计算得到锚固体中性点到硐室中心距离rm为7.39 m，数值计算得到rm为7.20 m，两者相差不大。数值计算与理论计算的轴应力均在中性点处达到最大值，锚固体两端轴应力均为0，变化趋势一致。数值计算与理论计算的最大轴应力分别为21.0和27.6 MPa，后者较前者的数据误差为23.9%，越接近锚固体中性点轴应力误差越大，越接近锚固体两端轴应力误差越小。

由图5(b)可看出，数值计算与理论计算得到的剪应力均随径向半径的增加而逐渐减小，变化趋势一致。理论计算得到的剪应力大于数值计算，数值计算与理论计算得到的最大剪应力分别为2.05和1.78 MPa，后者较前者的数据误差为13.1%，数值计算与理论计算剪应力的误差沿锚固体较为均匀，误差范围为13.1%～15.7%。

综上所述，数值计算与理论计算得到的锚固体应力趋势基本一致，误差在可控范围之内，这也验证了本文理论分析的可行性。

2.3 锚固体应力的影响因素分析

为研究锚固体应力的影响因素，选取不同的锚杆长度L、锚固体直径ds、围岩内聚力c和初期支护施作时距掌子面的距离X1进行数值计算，如图6—图9所示。

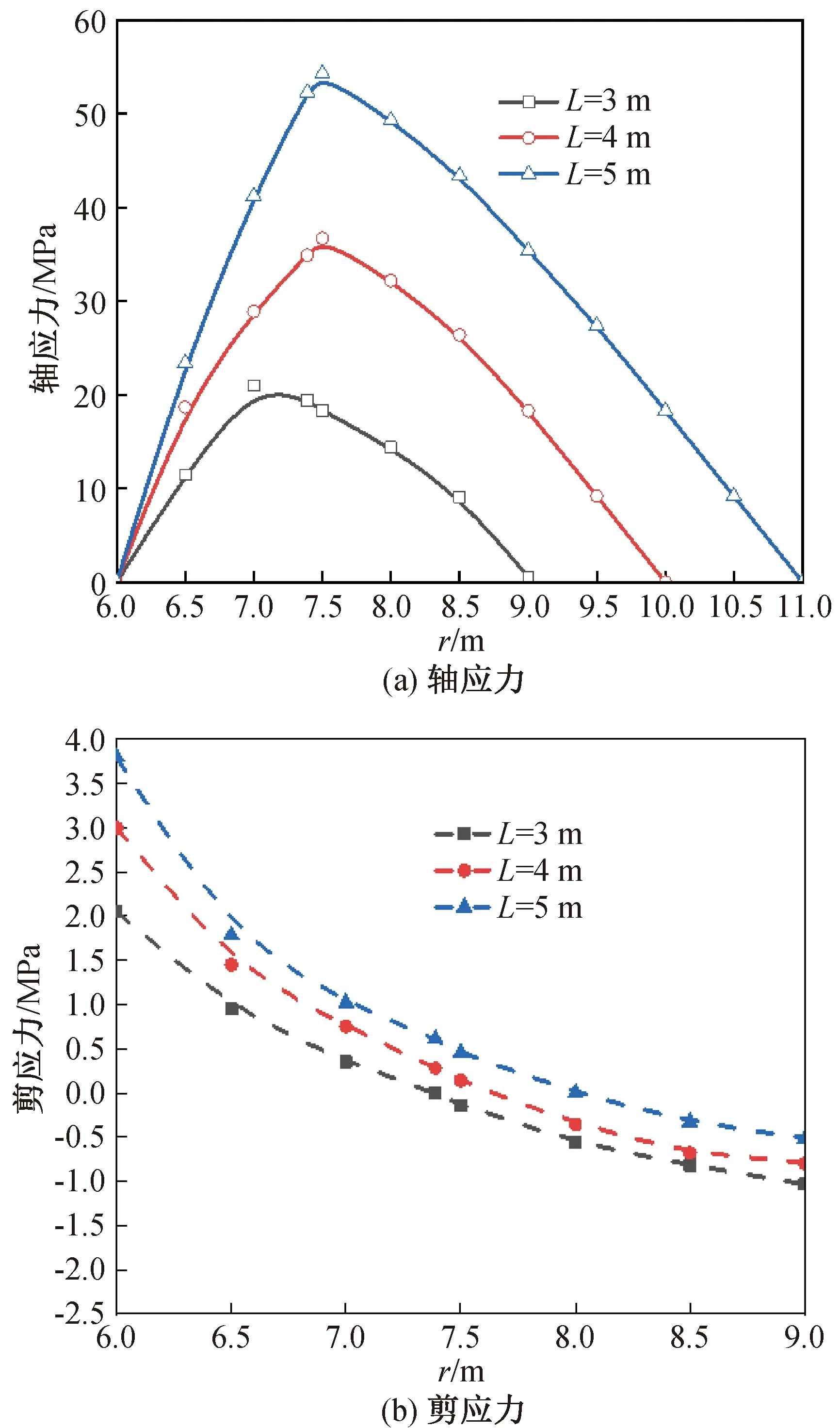
图6 不同锚固体长度下的应力分布Fig.6 Stress distribution of different anchor length

由图6(a)可看出，三种锚杆长度L取值下的轴应力均在中性点取得最大值，锚杆长度L越小，中性点越靠近隧洞中心。锚固体长度每增加1 m，最大轴应力增加约20 MPa。

由图6(b)可看出，三种锚杆长度L取值下的剪应力走势一致，r越小，剪应力越大。锚固体长度每增加1 m，剪应力增加0.5～1.0 MPa。

综合图6可看出，L越大，锚固体的轴应力和剪应力越大，且最大轴应力总体增幅较大，而剪应力增幅相对较小，由此看出锚固体长度对轴应力的影响明显大于剪应力。

由图7可看出，锚固体直径每增加5 mm，最大轴应力增加约2.5 MPa，剪应力增加在0.1 MPa至0.2 MPa之间。锚固体直径越大，锚固体的轴应力和剪应力越大，且最大轴应力总体增幅较小，中性点靠近洞中心的一段剪应力越大，而远离洞中心的一段剪应力越小。

从图9可看出，锚固体施作距离掌子面距离每增加3 m，最大轴应力增加约3 MPa，剪应力增加0.25 MPa。支护时机对锚固体应力影响规律与围岩内聚力及锚固体直径对锚固体应力影响规律类似，支护施作越早，锚固体轴应力越大。

综合分析图6—图9，锚固体两端轴应力均接近0，且在中性点处轴应力最大。锚杆直径越小，中性点越靠近隧洞中心。锚杆长度L对应力分布的影响最大，锚固体直径ds、围岩内聚力c和初期支护施作时距掌子面的距离X1对应力分布的影响次之。隧道设计和施工时，应合理考虑锚杆长度及其它要素，根据围岩条件科学选择支护时机，以免造成注浆锚杆屈服。

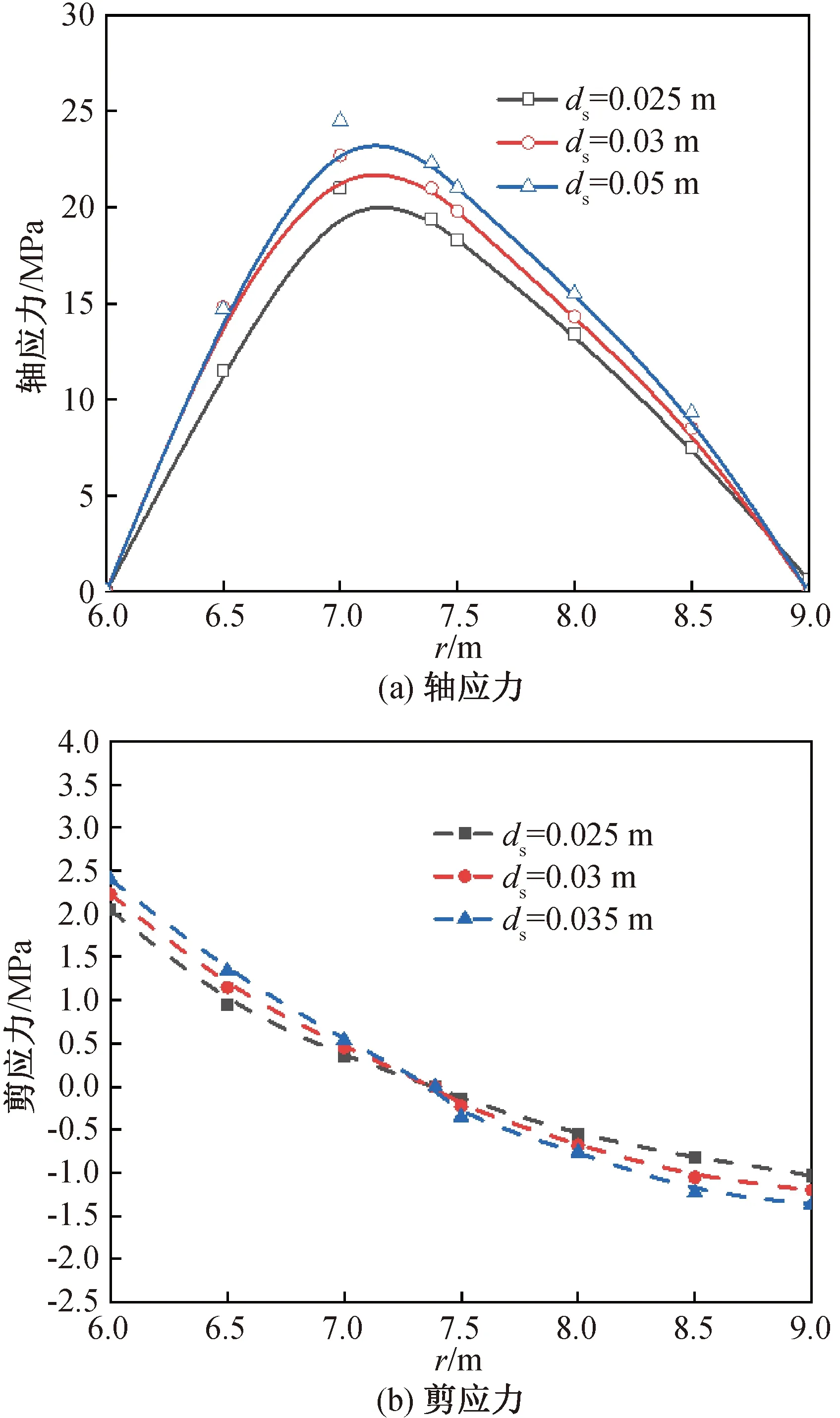
图7 不同锚固体直径下的应力分布Fig.7 Stress distribution of different anchor diameter

由图8可看出，随着锚固体内聚力的增大，锚固体的轴应力随着增大，中性点靠近洞中心的一段剪应力越大，而远离洞中心的一段剪应力越小。锚固体内聚力每增加10 MPa，最大轴应力增加约3 MPa。

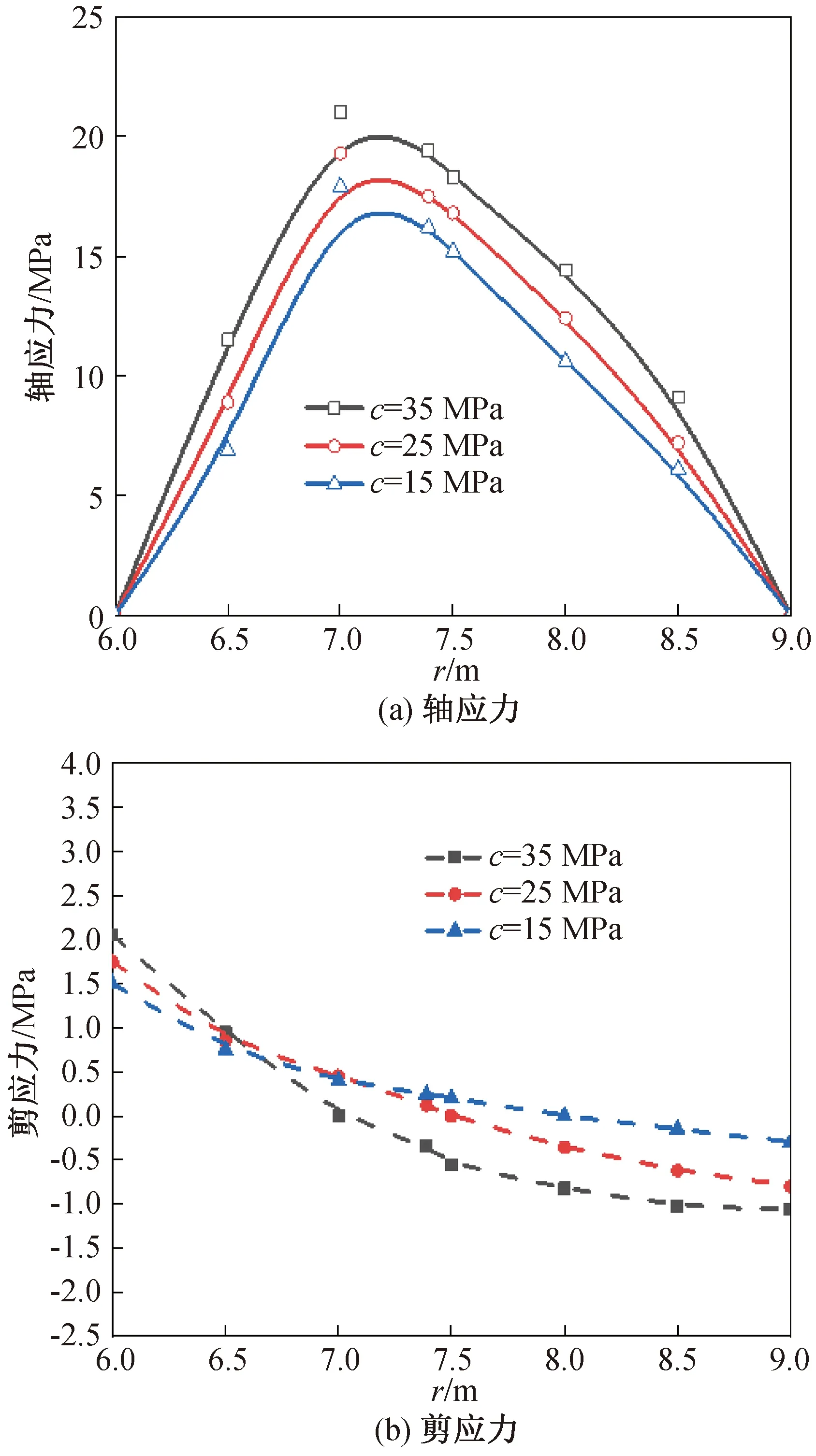
图8 不同围岩内聚力下的锚固体应力分布Fig.8 Stress distribution of anchor under different cohesion of surrounding rock

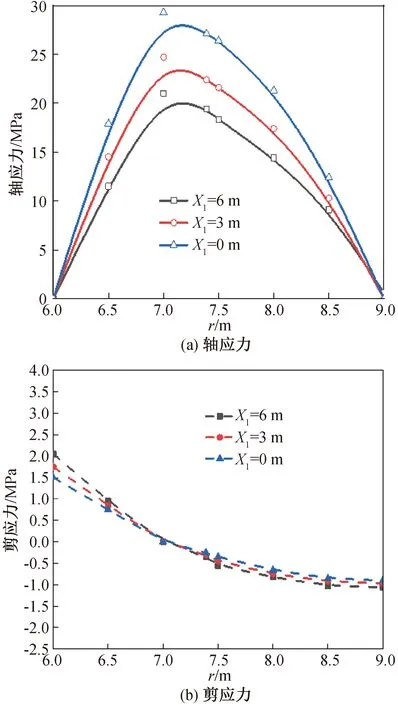
图9 不同X1值的锚固体应力分布Fig.9 Stress distribution of anchor solid with different X1 values

3 结论

1)本文以注浆锚杆为研究对象，将锚杆内部浆体、锚杆与锚杆外围覆盖浆体组成的复合体视为“锚固体”，根据锚固体结构特点和受力特征，结合岩体力学理论，得到一种新的锚固体应力分布理论解析方法。

2)构建隧道三维数值模型，通过数值模拟与理论分析对比研究锚固体应力分布规律，两种方式计算得到的锚固体应力趋势基本一致，误差在可控范围之内，验证了本文锚固体应力分布理论解析方法的可行性。

3)锚杆长度L对应力分布的影响最大，锚固体直径ds、围岩内聚力c和初期支护施作时距掌子面的距离X1对应力分布的影响次之。隧道设计和施工时，应合理考虑锚杆长度及其它要素，根据围岩条件科学选择支护时机，最大程度发挥注浆锚杆的锚固性能。