水泥基复合材料双钢板组合剪力墙最佳ECC高度研究

袁朝庆，代晓辉，章 桀，宋 爽

(东北石油大学 土木建筑工程学院，黑龙江 大庆 163318)

为了研究双钢板混凝土组合剪力墙的受力机理，聂建国[1-4]及其试验小组通过拟静力抗震性能试验，研究该类结构的抗震性能，并且得到一般破坏形态。研究结果表明，双钢板混凝土组合剪力墙的滞回曲线饱满，抗震性能较好。陈丽华等[5-8]对拉结件的双钢板混凝土组合剪力墙进行了试验研究，并进行了有限元数值模拟，发现L型及C型连接件均阻止了试件的局部屈曲。但是在高轴压比下，结构的承载能力和刚度退化方面差，混凝土底部塑性铰区增加。所以对于在高轴压比下的双钢板混凝土组合剪力墙结构中提高承载能力和较小底部塑性铰区是研究的一个重点。Victor Li[9]首次成功研制了水泥基增强复合材料(Engineered Cementitious Composites，简称ECC)，ECC材料是通过将水泥砂浆和小粒径的细骨料作为基体，掺入体积少于2%的纤维复合增强材料复合成的一种建筑材料。经过凝结硬化的ECC材料，在受压和受拉荷载作用下表现出了较高的延性。

目前，将ECC材料运用在双钢板混凝土组合剪力墙上的研究还较少。本文将ECC材料引入双钢板剪力墙的底部，试着去解决双钢板混凝土组合剪力墙的承载能力和刚度退化方面差，混凝土底部塑性铰区增加等问题。本文根据不同剪跨比的ECC-双钢板组合剪力墙滞回曲线，骨架曲线，承载能力，变形能力，刚度退化和耗能能力来分析ECC材料在双钢板组合剪力墙中的抗震性能，得到ECC材料作用在不同剪跨比的双钢板混凝土组合剪力墙结构中的最适高度。

1 有限元模拟验证

以文献[10]的盐城广播电视塔为原有模型，按照试验比例1∶1.25建立双钢板剪力墙模型DCSW1。本文建的双钢板剪力墙模型DCSW1*与文献[10]中的模型DCSW1尺寸和加载方式一样，分析结果与原模型进行对比分析。有限元模型如图1。

图1 DCSW1*有限元模型Fig.1 DCSW1* Finite element model

本文分析模块采用的是ABAQUS/Standard，钢板与混凝土都采用实体单元(C3D8R)，混凝土本构模型采用的是塑性损伤模型。钢材本构模型选用的是金属塑性模型，常温静载状态下，钢材的单向拉伸的应力应变曲线如图2所示，本文为了验证往复荷载作用下双钢板混凝土组合剪力墙系列抗震性能的可行性，采用文献[10]给出的钢材应力应变关系图，根据输入的材性试验得到曲线图上相对应的数据点，具体曲线图如图3所示。底部边界条件采取完全固定的方式。钢板与混凝土的关系为粘结滑移，混凝土和钢板法向接触设置为“硬接触”，切向接触设置为“罚”接触。在剪力墙顶面设置参考点与顶面耦合，施加竖向荷载和水平荷载到参考点上。

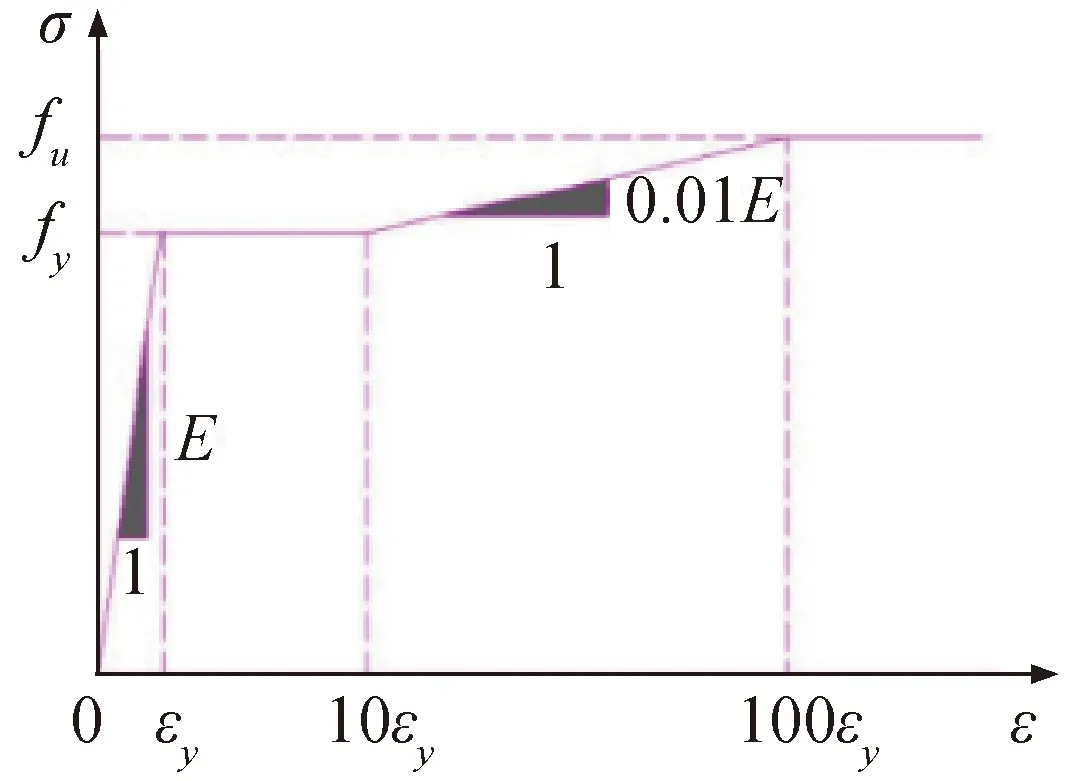
图2 钢材应力-应变曲线Fig.2 Steel stress-strain curve

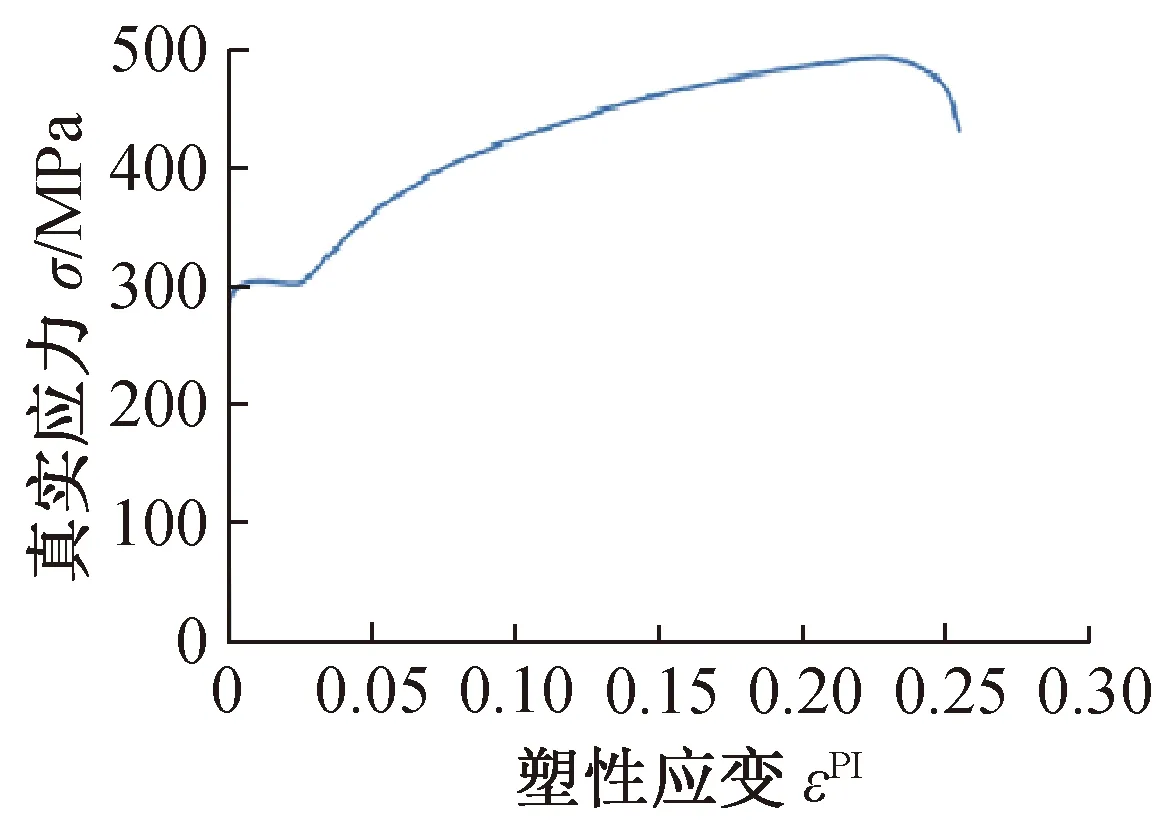
图3 钢材应力-应变曲线Fig. 3 Steel stress-strain curve

图4(a)为文献[10]的原有模型DCSW1，图4(b)是文献[10]对DCSW1模拟结果DCSW1m，图4(c)为本文的验证模型DCSW1*的滞回曲线，图5是骨架曲线。由图4和图5可以看出：试验的滞回曲线和本文验证的滞回曲线接近一致，有限元模拟情况下的滞回曲线更加光滑饱满。由骨架曲线图可以看出，三条骨架曲线形状相同，有限元模拟的骨架曲线DCSW1*与试验的骨架曲线相似，误差在20%的范围内，可以认为ABAQUS模拟双钢板剪力墙在往复荷载作用下是能进行抗震性能研究的。由表1可知，误差在控制范围以内。

图4 滞回曲线图Fig.4 Hysteresis graph

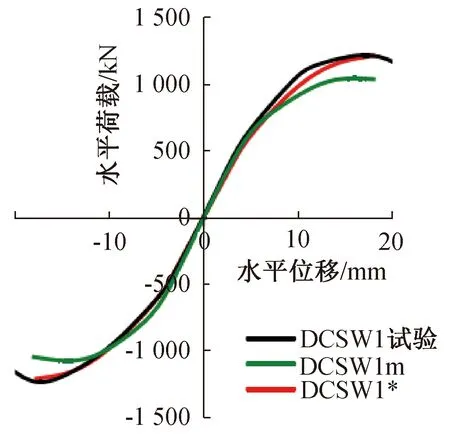
图5 骨架曲线对比Fig.5 Comparison of skeleton curves

根据表1所知，初始刚度下DCSW1m与试验结果DCW1相近，仅有1.6%。本文利用ABAQUS模拟出的有限元模型DCSW1*的屈服荷载与DCSW1相差2.72%，屈服位移相差5.78%，极限荷载相差4.84%，极限位移相差1.63%，最大不超过6%。由此可知，DCSW1*的数据较为准确，也说明利用ABAQUS可以准确模拟双钢板剪力墙试件。

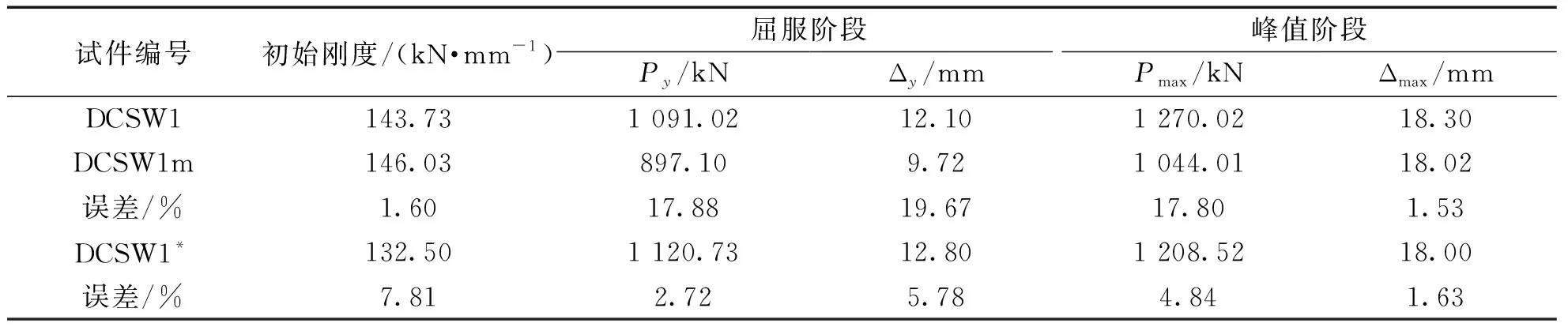
表1 试验结果与有限元结果对比

2 有限元模型建立

为了与ECC双钢板-混凝土组合剪力墙进行对比，首先建立普通双钢板-混凝土组合剪力墙模型，并命名为BASE。模型采用钢板强度为Q345，为简化模型，使用隔板连接双钢板-混凝土组合剪力墙，剪力墙模型如图6和图7所示，具体尺寸如表2所示。

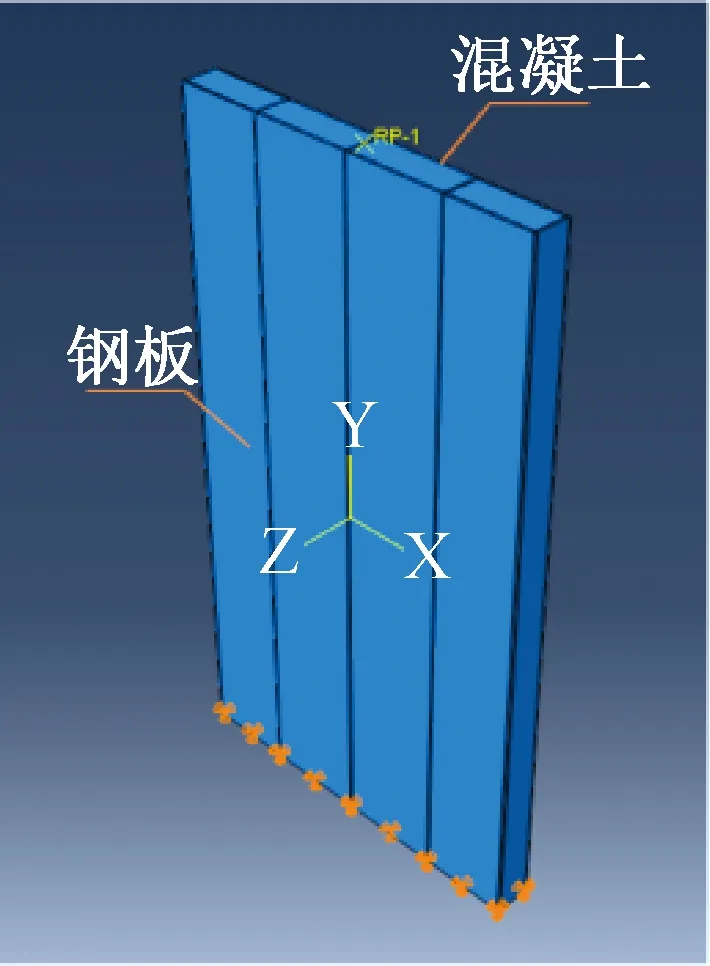
图6 双钢板混凝土组合剪力墙Fig.6 Composite shear wall with double-steel slab concrete

ECC双钢板-混凝土组合剪力墙的材料本构参照丁发兴[11]的模型本构，ECC材料的受拉本构参照文献[12]推导的单轴受拉本构方程式。受压本构参照的是李艳课题组提出的ECC单轴受压荷载下的本构方程式，如下：

(1)

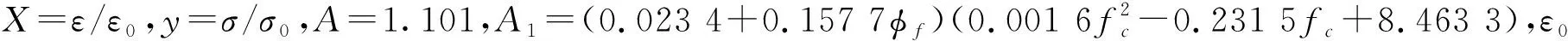
在剪力墙上表面通过建立一个耦合点，将上表面耦合于一点上，对结构施加的竖向荷载和水平位移作用在耦合点上。在ABAQUS加载这一块，模型采用在分析步step-2上进行位移加载，即通过施加位移加载方式并且设置幅值来进行往复荷载，通过幅值的计算时长在分析步中进行适当调整。

考虑经济适用性，ECC在双钢板-混凝土组合剪力墙底部高度取3%、7%、10%、15%。如图7所示，将ECC设置于剪力墙底部，与剪力墙混凝土的设置方式为绑定接触。设置不同剪跨比，改变ECC的不同高度，确定不同剪跨比下，ECC在双钢板-混凝土组合剪力墙底部最适高度。对各组ECC试件命名为HE(Height of ECC)，ECC在双钢板剪力墙中高度取3%的试件命名为：HE1-1、HE1-1.5、HE1-2.0；ECC在双钢板剪力墙中高度取7%的试件命名为：HE2-1、HE2-1.5、HE2-2.0；ECC在双钢板剪力墙中高度取10%的试件命名为：HE3-1、HE3-1.5、HE3-2；ECC在双钢板剪力墙中高度取15%命名为：HE4-1、HE4-1.5、HE4-2.0。具体模型图如图8所示，具体参数如表2所示。

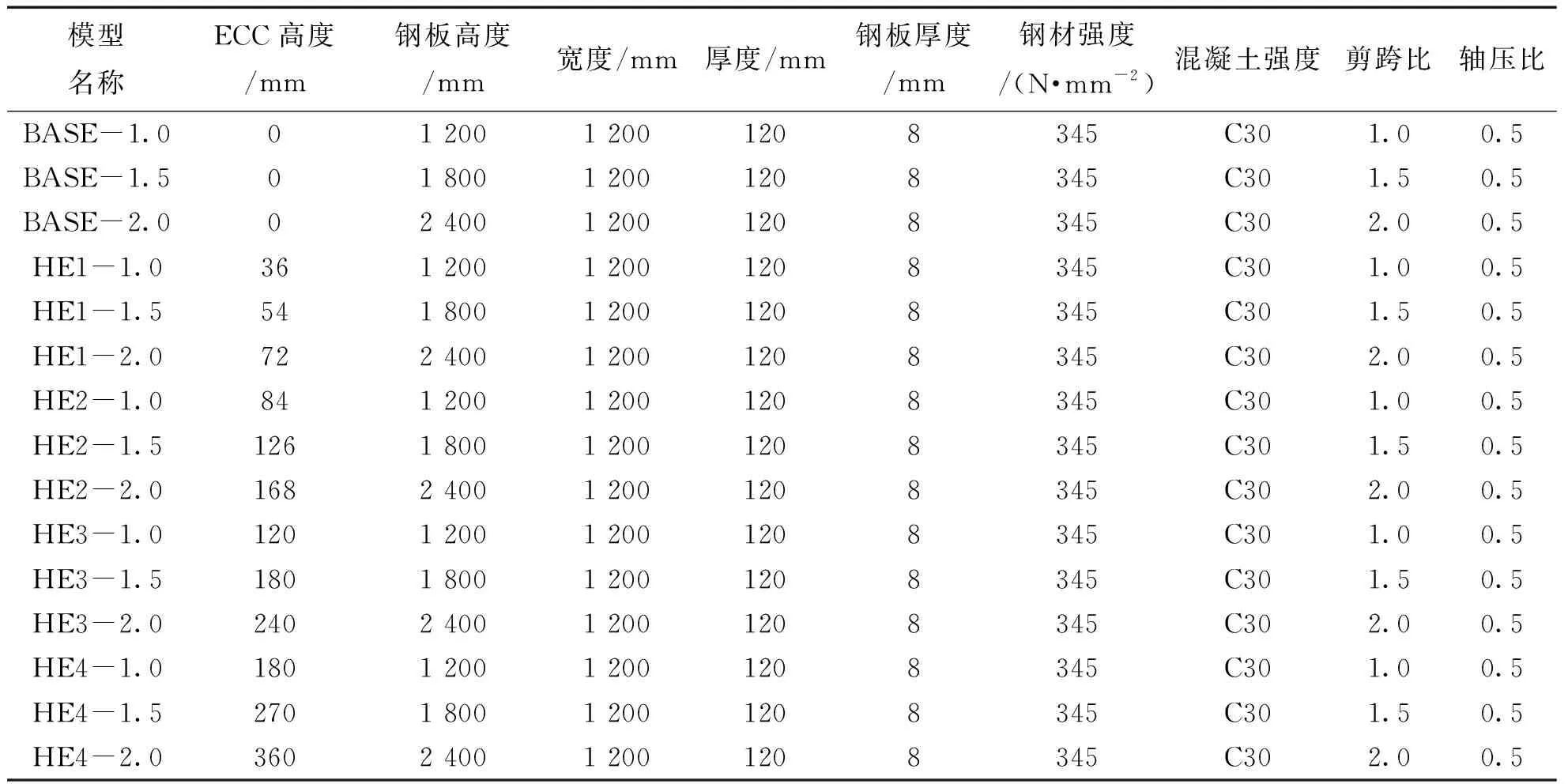
表2 模型参数表

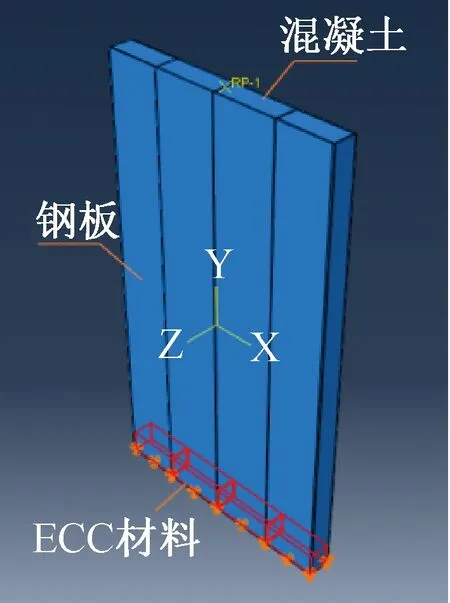
图7 ECC-双钢板混凝土组合剪力墙Fig.7 ECC- Composite Shear Wall with Double Steel Concrete

3 有限元结果和抗震性能分析

3.1 水平荷载-位移曲线分析

3.1.1 滞回曲线

由图8可知，各组ECC试件对比BASE试件，加入ECC材料的试件呈饱满梭形，极限位移增大，塑性能力增强，达到峰值荷载后的承载力降低缓慢。但是饱满的增加程度随着ECC高度的增加而减小。随着剪跨比的增大，加入ECC材料的试件饱满程度有所下降，结构的极限位移变小，塑性能力变差。因此对比于BASE试件，低剪跨比的ECC双钢板-混凝土组合剪力墙变形能力更好，延性更好，抗震性能更好。

图8 不同ECC高度的滞回曲线图Fig.8 Hysteresis curves of different ECC heights

3.1.2 骨架曲线

研究非弹性地震反应时，一般将滞回曲线和骨架曲线作为重要指标。模型BASE，HE1—HE4的骨架曲线对比图见图9。

由图9可知，各组试件的骨架曲线均呈倒S形，经历了弹性阶段和弹塑性阶段和承载力下降三个阶段。在弹性阶段，低剪跨比ECC试件骨架曲线要比BASE试件增长速度较快，中高剪跨比的ECC试件和BASE试件骨架曲线趋近于重合，说明初始阶段，低剪跨比试件ECC已经开始工作，而中高剪跨比的试件，弹性阶段，ECC在整体结构中发挥作用不大。但是在弹性阶段以后，其峰值荷载和峰值位移相较于BASE试件均有明显提升，且塑性段的拐点出现较晚，说明ECC试件相较于BASE试件其整体延性较好，底部没加ECC的BASE试件的峰值承载力低于ECC双钢板-混凝土组合剪力墙试件。随着水平位移的增加，ECC高度越高，其结构承载力越高。随着剪跨比的增大，试件承载力逐渐下降，所以低剪跨比的ECC试件较优。

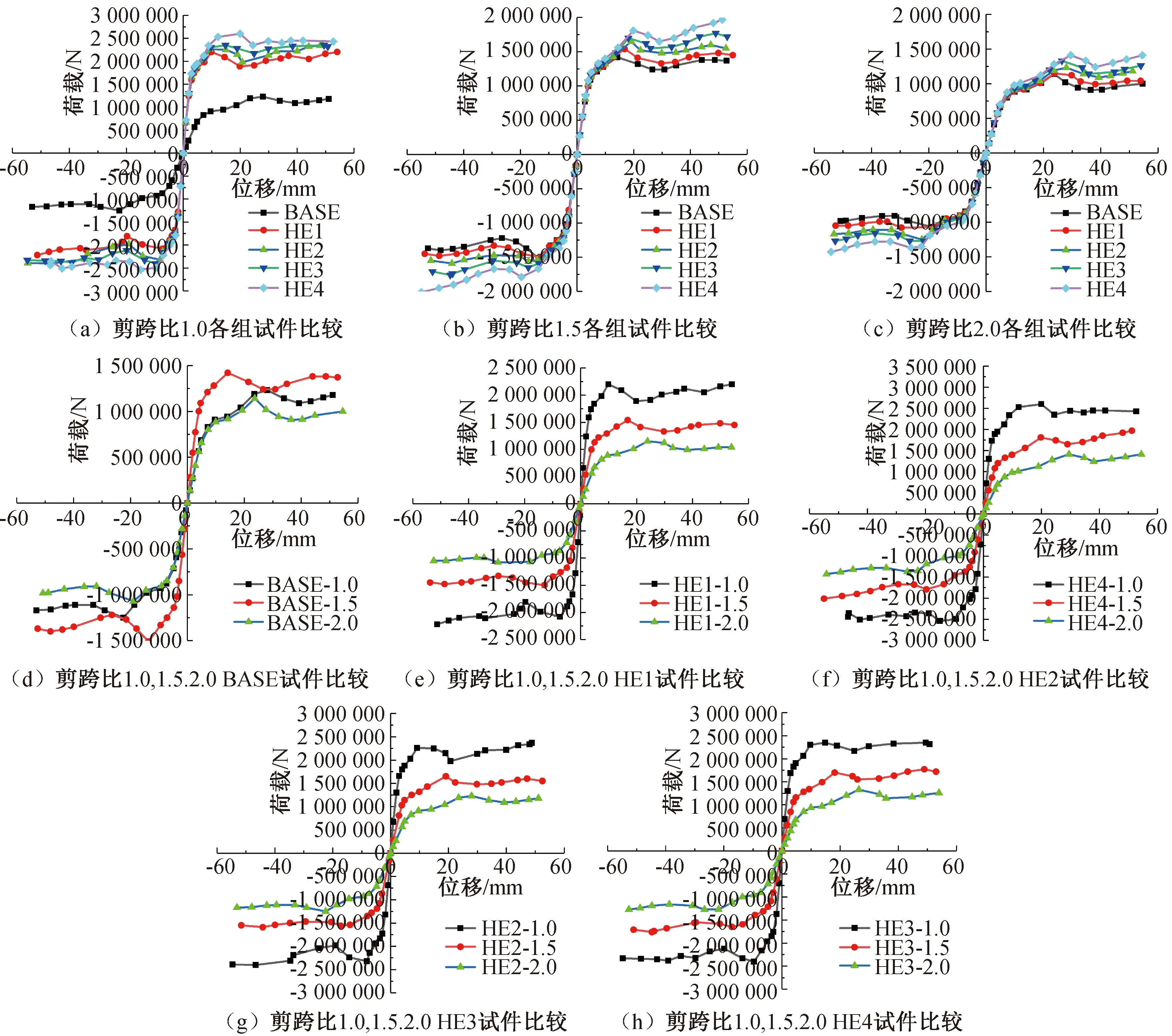
图9 不同ECC高度的骨架曲线对比图Fig.9 Comparison of skeleton curves at different ECC heights

3.2 承载能力对比分析

在结构设计中，承载力是研究抗震性能的重要指标。在骨架曲线的基础上，采用割线刚度法，通过确定组合剪力墙的名义屈服点来找出模型的屈服点。即pu=0.85pm，85%的峰值荷载点为极限荷载点，pu为极限荷载，pm为峰值荷载。

由表3列出的参数表明了BASE模型和HE系列模型的各种承载力特征点。可以从表3得出，相较于BASE模型，HE1—HE4系列模型的屈服荷载分别提高了92.53%、2.63%、0.64%、100.67%、6.48%、4.52%、103.54%、3.91%、7.60%、117.79%、18.99%、16.36%，峰值承载力提高了75.40%、3.75%、0.90%、 92.34%、10.58%、0.12%、91.53%、20.48%、17.65%、 107.26%、33.79%、26.24%。由此可以得出，当ECC高度增加，构件的屈服荷载和峰值荷载逐渐增加，峰值承载力也逐渐增加。

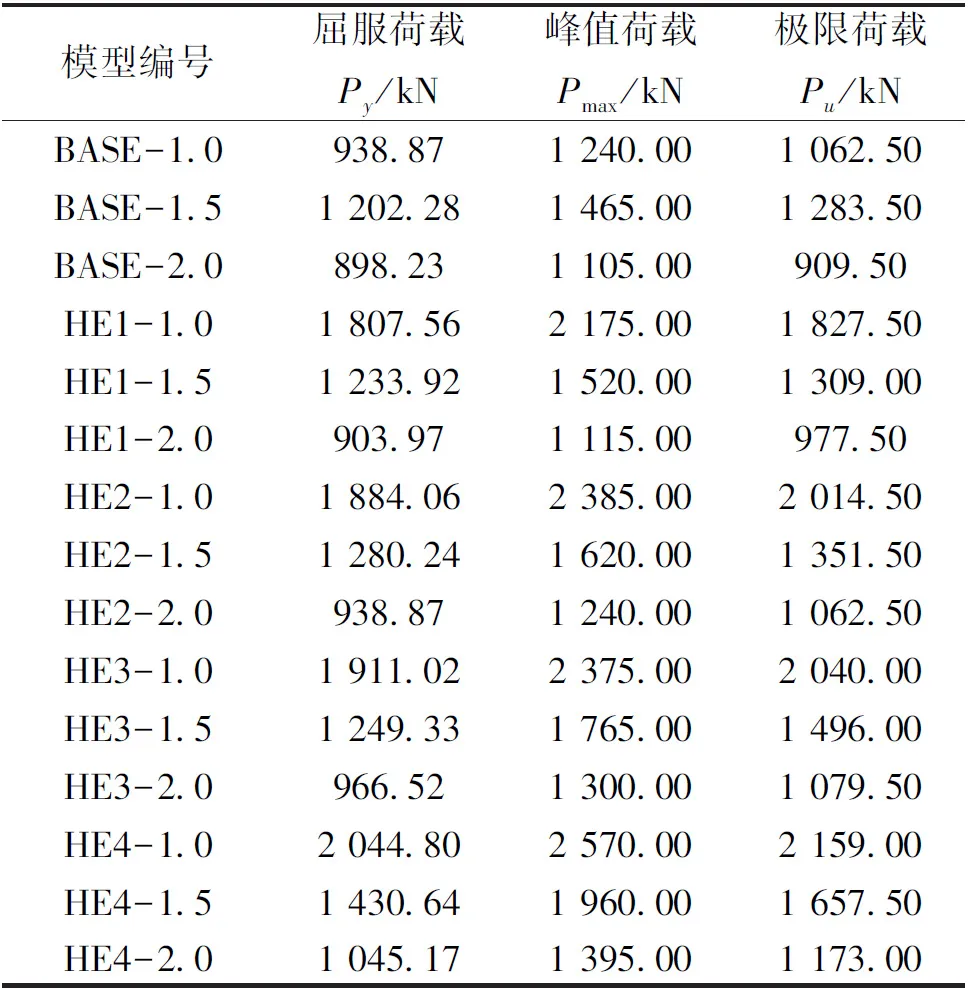
表3 各模型承载力特征点的有限元结果

3.3 变形与延性分析

结构在发生屈服破坏后，在满足承载力要求下，要有良好塑性变形能力，即为延性。延性的具体求出方法按照位移延性比来计算，即

(2)

其中，Δu为极限位移，Δx为屈服位移，β为延性。

通过BASE，HE系列模型提取计算出具体位移参数和延性参数如表4所示。

由表4可知，相较于BASE试件，HE系列试件延性均有所增加。HE1系列模型延性提高了180.9%、35.9%、54.7%；HE2系列模型延性提高了147.1%、15.4%、35%；HE3系列模型延性提高了156.9%、42.7%、28.6%；HE4系列模型延性提高了109.8%、3.5%、23.79%。由此可以得出，在剪跨比为1.5时，HE3提升幅度最大，即ECC高度在10%时，结构的延性提升效果最好。在剪跨比为1.0和2.0时，HE1提升幅度最大，即ECC高度在3%时，结构的延性提升效果最好。由此可见，ECC的加入明显提高了构件的延性。

表4 各模型变形能力计算的有限元结果

3.4 刚度退化分析

为了分析结构在往复荷载作用下抵抗变形的能力，采用公式(3)分析了BASE和HE系列模型的刚度退化关系，得到下列刚度退化曲线对比图，如图10所示。刚度退化曲线即滞回曲线每次循环加载的峰值荷载点与峰值位移的比值按照加载级别顺序连接。

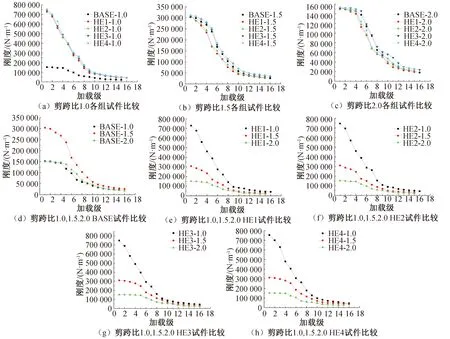
图10 不同ECC高度的刚度退化曲线对比图Fig.10 Comparison of stiffness degradation curves for different ECC heights

(3)

式中，Pi等于第i次循环的峰值荷载，Δi为第i次加载对应的峰值位移。

由图10可知，相比BASE试件，低剪跨比时，HE1系列的初始刚度较高，但后期退化程度较大。HE1系列刚度退化曲线基本重合，说明低剪跨比时，改变ECC高度对刚度退化影响不大。中高剪跨比时，HE2系列和HE3系列刚度退化曲线和BASE刚度退化曲线接近一致，这说明ECC高度的增加对于双钢板-混凝土组合剪力墙的刚度退化影响很小，这是因为随着位移的增加，钢板对结构的约束逐渐增加，并且最终形成有效约束，从而导致ECC的加入对于整个结构的刚度影响很小。BASE系列试件在剪跨比为1.5时初始刚度较大，后期与剪跨比为1.0和2.0刚度退化曲线接近一致。HE系列试件，随着剪跨比的增大，初始刚度逐渐减小，各组HE系列试件后期刚度退化程度接近一致。

3.5 耗能能力对比分析

剪力墙的耗能指标有很多，如等效粘滞系数，能量耗散系数，累积耗能等。本文选用等效粘滞系数来定量分析ECC双钢板混凝土组合剪力墙的耗能能力，等效粘滞系数越大，剪力墙在往复荷载下产生的滞变阻尼越大，剪力墙的耗能能力越好，在地震作用下的安全性更加优良，其计算见图11和公式(4)。

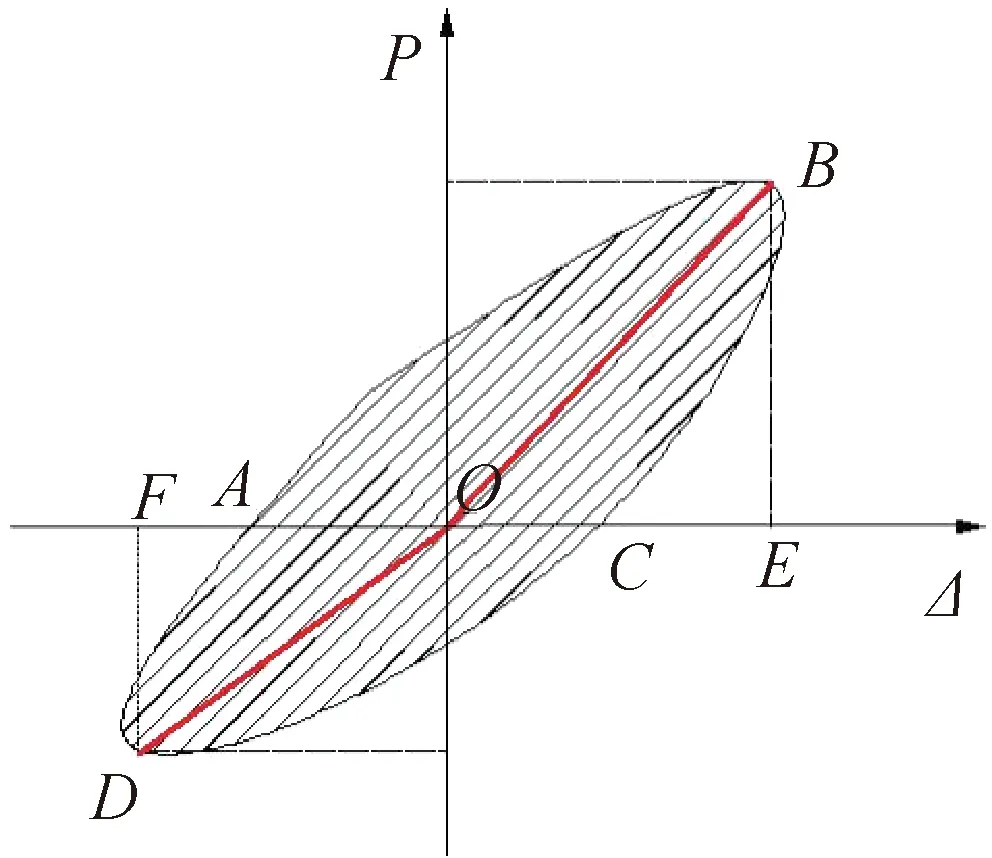
图11 等效粘滞系数示意图Fig.11 Schematic diagram of the equivalent viscosity coefficient

(4)

图12为HE系列ECC双钢板-混凝土组合剪力墙的等效粘滞系数he随着层间位移角的变化关系。如图所示，随着加载级的增加导致结构的水平位移随之增大，随着剪跨比增大，粘滞系数略有下降。对于BASE试件在剪跨比为1.5时，粘滞系数最大。低剪跨比时，ECC双钢板-混凝土组合剪力墙等效粘滞系数明显高于普通双钢板-混凝土组合剪力墙。剪跨比为1.0时，其中HE1-1.0提升幅度最大，为28%。即ECC最佳高度取36 mm。剪跨比为1.5时，HE3-1.5提升幅度最大，为9.6%，即ECC最佳高度取180 mm。剪跨比为2.0时，HE1-2.0提升最高，为13.3%，即ECC最佳高度取72 mm。

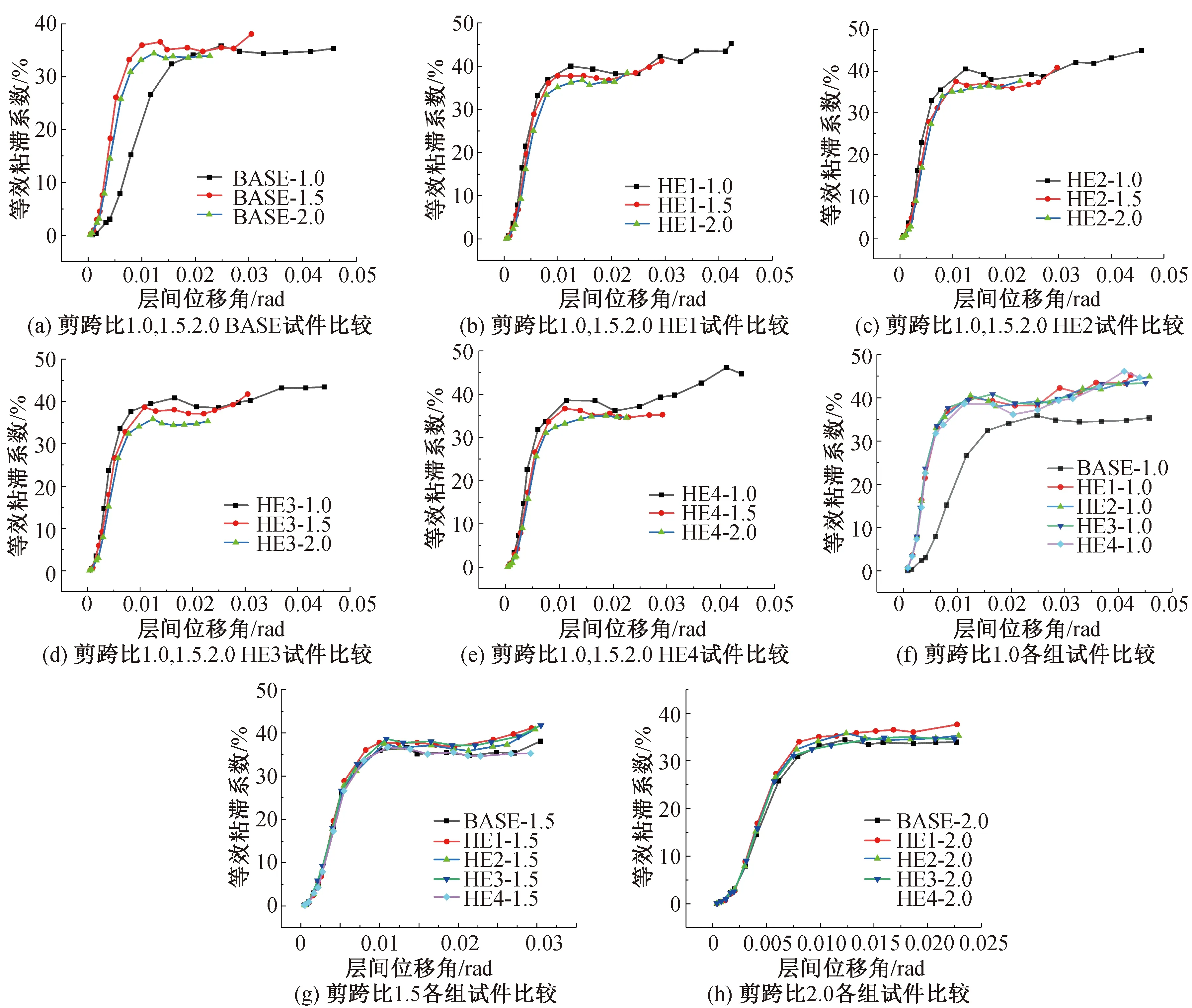
图12 不同ECC高度下的等效粘滞系数对比图Fig.12 Comparison of equivalent viscosity coefficients at different ECC heights

4 结论

本文将ECC材料引进普通双钢板-混凝土组合剪力墙，在不同剪跨比的情况下，通过在底部易破坏位置设置不同高度的ECC材料来研究模拟出其抗震性能，具体结论如下：

1)对比普通双钢板组合剪力墙，ECC双钢板-混凝土组合剪力墙的峰值荷载和屈服荷载均有所提升，并随着ECC高度的增加而提高，剪跨比为1.0时，屈服荷载最大提升了117.79%，峰值荷载最大提升了107.26%。

2)ECC双钢板-混凝土组合剪力墙在变形能力方面表现优良，ECC的加入大幅提升了整个结构的延性。剪跨比为1.0，ECC高度在3%时提升效果最好，延性提高了180.9%，剪跨比为1.5时，ECC高度在10%时提升效果最好，延性提高了42.7%，剪跨比为2.0时，ECC高度在13%时提升效果最好，延性提高了54.7%，说明剪跨比为1.0，ECC高度为3%的双钢板-混凝土组合剪力墙能够最大程度上提升结构的延性，改善了结构的变形能力。

3)从刚度退化曲线整体来看，ECC双钢板-混凝土组合剪力墙在刚度退化方面与普通双钢板组合剪力墙相差不大。在耗能方面，通过计算不同模型的等效粘滞系数，显示出了ECC材料的加入均不同程度地提高了结构的耗能能力，剪跨比为1.0时，其中HE1-1.0提升幅度最大，为28%。即ECC最佳高度取36 mm。剪跨比为1.5时，HE3-1.5提升幅度最大，为9.6%，即ECC最佳高度取180 mm。剪跨比为2.0时，HE1-2.0提升最高，为13.3%，即ECC最佳高度取72 mm。