基于熵权法与粗糙集理论的海洋发展评价指标体系筛选与构建

高 升，刘 伟，曹广喜

（1.南京审计大学 自然资源与环境审计研究院，江苏 南京211815；2.南京审计大学 政府审计学院，江苏 南京211815；3.南京信息工程大学 管理工程学院，江苏 南京210044）

21世纪是全面开发利用海洋的世纪，沿海国家纷纷将海洋可持续发展作为国家战略。海洋发展推动了社会经济繁荣，但不可避免地对海洋资源与环境带来了影响。随着海洋资源开发的不断加剧，海洋环境问题日益突出，海洋发展评价是实现海洋高质量发展，促进海洋经济-资源-环境协调发展的前提[1]，而合理筛选与构建指标体系是进行海洋发展评价的基础与关键。国内外关于海洋发展评价指标体系的研究重点多以产生的社会经济效益评估为主，将资源、环境、政策纳入海洋发展评价的研究较少[2]。海洋发展评价指标的筛选需要符合科学性、整体性、综合性、代表性、可操作性和实用性、独立性、可比性、层次性、动态性，以及稳定性等原则[3]。针对不同的评价对象、评价区域的特点、评价指标的数量与因果联系，国内外形成了多种多样的评价指标体系，如PSR（Pressure-State-Response）模型指标体系[4]，联合国可持续发展委员会建立的DSR（Drivingforce-State-Response）模型指标体系[5]，欧洲环境署建立的DPSIR（Driving force-Pressure-State-Impact-Response）模型指标体系[6]，SOPAC（南太平洋应用地球科学委员会）建立的具有沿海地区特色的生态脆弱性评价指标体系[7]等，这些体系均较为成熟且被广泛应用。在后续研究中，又不断衍生出D-PSE-R（Driver-Pressure-State-Exposure-Response）模型指标体系[8]、DPSEEA（Driving force-Pres sure-State-Exposure-Effect-Response）模型指标体系[9]、DPSR（Driving force-Pressure-State-Response）模型指标体系[10]、PFC（Pressurefeedback-Regulation）模型指标体系[11]、SDR（State-Hazard-Response）模型指标体系[12]、PSE（Pressure-Sensitive-Elasticity）模型指标体系[13]等。依赖模型框架建立指标体系被广泛运用，但是在大量的研究中却表现出一个明显的不足——没有统一和完善的海洋发展评价指标体系。因此，建立统一标准的评价指标体系，加强对模型的可信度与准确度的评价，控制评价过程中的质量控制等是今后指标模型框架运用研究的一大重心和发展方向。

我国对海洋发展状况缺乏有效的评价。一方面，海洋发展中的经济效益评价往往只是从财务效益评价的角度出发，缺乏全面有效的国民经济评价，忽略了外部不经济性。另一方面，在海洋发展评价的过程中，虽然海洋经济效益的价值较易计算，但是在社会损益、海洋资源损益、海洋环境损益等方面考虑较少，难以充分体现[14]。

基于客观筛选构建的指标体系进行的海洋发展评价，为及时优化海洋资源开发合理管理、调整海洋经济发展政策、促进海洋生态环境保护提供了参考，对推动海洋社会经济与海洋资源环境的协调发展具有重大意义。本文的创新之处在于将德尔菲法、熵权法与粗糙集理论相结合对评价指标进行筛选约简，构建起一个涵盖社会损益、经济损益、资源损益、环境损益的全方位、立体化的多级海洋发展评价指标体系，为海洋发展评价指标体系的筛选与构建提供了一种方法借鉴，减少了人为主观性影响，为科学合理地评价海洋发展状况提供重要参考。

1 研究方法与数据来源

1.1 研究方法

依据国内外指标体系构建模型与指标筛选的相关研究成果，综合考虑沿海社会状况、经济发展、资源开发、生态环境等方面，运用德尔菲法逐一选取相应的社会损益指标、经济损益指标、资源损益指标、环境损益指标。对各评价指标分别进行无量纲化处理并计算指标熵权权重，按照权重大小对评价指标进行重要程度排序，在避免主观干扰的同时剔除权重较小的指标。运用粗糙集原理去除信息冗余，进一步筛选约简评价指标，形成最终需要的海洋发展评价指标体系。熵权法与粗糙集原理皆从数据上客观分析，排除人为主观性，两种方法相结合可使评价指标体系更客观的精简。

1.1.1 熵权法

为了使具有不同单位量值的评价指标具有可比性，消除不同单位数据量纲的影响，使各指标具有一个可比的尺度，需要对指标进行无量纲化处理，即指标的标准化。本文采用极差标准化法将评价指标数据转化为0～1区间的标准化可比数值，其方法如下：

对于效益型指标采用：

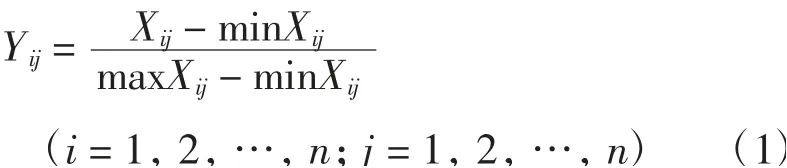
对于成本型指标采用：

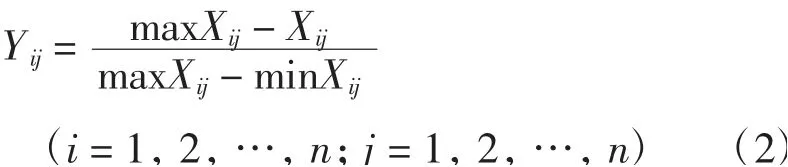
式中：Yij为第i指标的评估值；Xij为标准化系数；maxXij为最大值；minXij为最小值。

指标熵权权重Wj计算公式[15]如下：

式中：eij为第j项指标标准值yij在第i个样本年份标准值合计数的比重；hij为第j项指标的信息熵值；wij为指标权重且0≤wij≤1，∑wij=1；n为样本数，m为评价指标数，i=1，2，…，n，j=1，2，…，m。

1.1.2 粗糙集理论

粗糙集理论既可以对数据进行分析和推理，从中揭示潜在的规律，又可以计算指标重要性。约简步骤主要是首先进行指标数据的归一化处理，得到指标标准值，然后对评价指标整体进行离散化处理，最后通过区分矩阵法对评价指标进行指标约简。构造可辨识矩阵得到区分函数，虽然可以直接计算决策表的约简与核，但是只适用于非常小的数据集，所以通过吸收律对区分函数进行化简。

令S=（U，B，W，F）为一个知识表达系统，其中U作为论域表示全体样本的集合；B表示属性集合；W表示属性值集合；F表示信息函数。|U|=n，S的区分矩阵是个n阶矩阵，其中某元素：

式中：b（x，y）表示属性集合；D表示区分函数，对于每个属性b∈B。

若b（x，y）={b1，b2，b3，…，bm}≠Ø，则指定一个布尔函数b1∨b2∨b3∨…∨bm，用∑b（x，y）表示。核是区分矩阵中所有单个元素的集合，即：

Core（B）={b∈B/b（x，b）={b}；x，y∈U}（6）

1.2 数据来源

选取15个海洋开发与发展评价样本作为海洋发展评价体系筛选与构建的研究对象。相关数据来源于《中国海洋统计年鉴》、相关区域用海规划报告、海洋发展报告、各海洋开发项目的财务数据、实际监测数据、可行性研究报告、海洋环境影响评价报告、海域使用论证报告、调研报告、海域利用示范报告以及环保部门的监测数据和排污申报数据等。

2 海洋发展评价指标体系的筛选约简

基于国内外海洋发展评价指标体系构建成果及咨询相关领域专家，深入分析海洋发展涉及的社会、经济、资源、环境等方面的成本与效益指标，运用德尔菲法[16]选取与海洋发展密切相关的40个成本与效益指标，形成一个初始的多级海洋发展评价指标体系（表1），体系包含目标层、准则层、要素层和指标层四层。其中，第1层为目标层，综合反映海洋发展评价状况；第2层为准则层，由社会损益、经济损益、资源损益、环境损益四部分组成；第3层为要素层，通过社会效益指标、经济效益指标、资源效益指标、环境效益指标反映海洋发展效益状况，通过社会成本指标，经济成本指标、资源成本指标、环境成本指标反映海洋发展成本状况；第4层为因子层，由通过筛选的40个评价指标组成。运用极差标准法对评价指标进行无量纲化处理，将熵权法与粗糙集理论相结合作为评价指标体系的筛选约简方法。

2.1 熵权法筛选约简

在通过德尔菲法初步筛选的40个评价指标基础上，对各指标数据进行标准化处理之后，采用熵权法计算出40个因子层指标熵权权重，依据各要素层各因子指标的权重大小，分别从8个要素层中各自挑选出权重值排序前4名的指标，筛选出32个指标构成新指标体系（表1）。

表1 海洋发展评价指标体系的熵权筛选约简

2.2 粗糙集理论筛选约简

将指标体系综合数据作为对象，32个评价指标作为属性，生成一个二维表，利用等距划分法对标准化数据进行离散化，指标数据被离散为1、2、3、4这4个级别，分别代表阈值为[（0，0.25），（0.25，0.5），（0.5，0.75），（0.75，1.0）]。基于社会效益等8个准则层的离散化信息表，得到海洋发展评价指标数据离散化结果。从可辨识矩阵可以看出，矩阵的每一项是区分对应两个对象的属性集合。根据可辨识矩阵，可很容易地得到决策表的相对核，相对核是计算所有约简的基础。如果一个属性在矩阵中出现得越频繁，表明该属性区分的对象越多，该属性的区分能力也就越大，该属性就越重要。因此，可将属性在可辨识矩阵中出现的频率作为该属性的重要性度量。

应用粗糙集理论中的公式4、5、6对表2中的32个指标进行约简，约简过程如下：为方便运算，令[a，b，c，d]=[Yi1，Yi2，Yi3，Yi4]，分别独立计算出信息表2中各分表的分辨矩阵（表2）。

表2 海洋发展评价指标体系中社会效益指标分辨矩阵

基于构造的分辨矩阵，通过区分函数求得约简属性与核集。从海洋发展评价指标体系中社会效益指标分辨矩阵中得到该矩阵的核为a、c、d，所以社会效益指标最小约简为居民生活水平改善率，居民利益协调完成度，新增就业率。同理，从社会成本指标分辨矩阵中可知：核为c，M=a∨b∨d，社会成本指标最小约简为年游客人数变化率，管理和用海矛盾，居民生活受到不良影响。从经济效益指标分辨矩阵中可知：核为c和d，M=a∨b，经济效益指标最小约简为单位岸线的经济净收益，年均缴纳税收额，单位面积经济净收益。从经济成本指标分辨矩阵中得到核是a、b、d，所以经济成本指标最小约简为环境污染防治费用、海域使用金、单位海岸线的海洋灾害经济损失。从资源效益指标分辨矩阵中得到核是a、b、d，所以资源效益指标最小约简为海域空间开发率、水产品总产量变化率、生物多样性指数。从资源成本指标分辨矩阵中得到核是a、b、d，所以资源成本指标最小约简为浅海滩涂湿地变化率、海洋旅游资源价值损失、单位面积海洋生物资源损失。从生态环境效益指标分辨矩阵中可知：核为a、b，M=c∨d，生态环境效益指标最小约简为年游客人数变化率，管理和用海矛盾，居民生活受到不良影响。从生态环境成本指标分辨矩阵中得到核是b、c、d，所以生态环境成本指标最小约简为生态系统服务功能价值损失、冲淤系数、区域内特征点最大流速值变化率。

在熵权约简指标的基础上，通过粗糙集理论对评价指标体系进行第二次筛选，最终得到海洋发展评价指标体系（表3）。

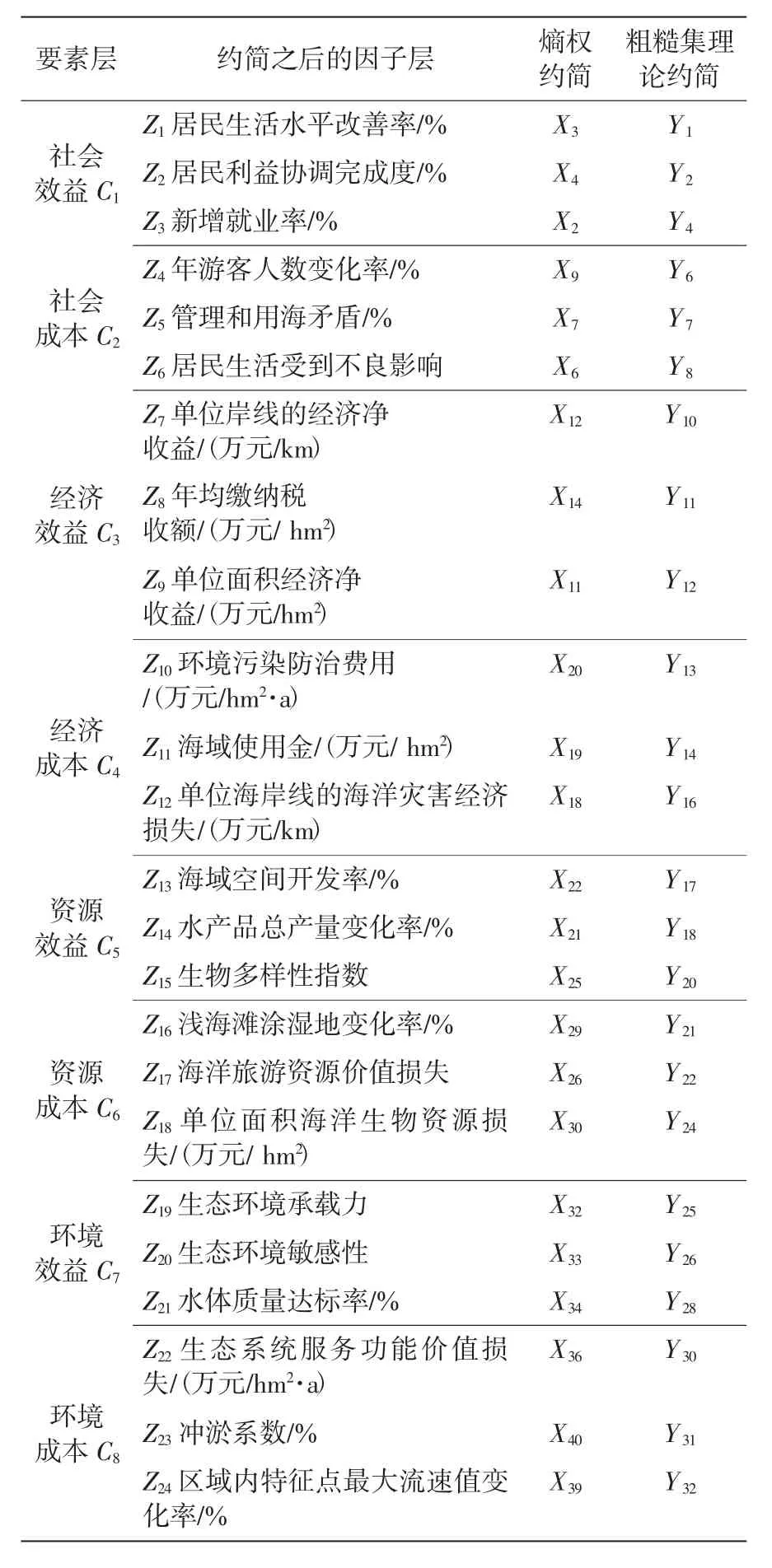
表3 经过熵权法与粗糙集理论筛选约简后的海洋发展评价指标体系

3 讨论

海洋经济的快速发展对海洋资源的开发需求不断增大，海洋资源的开发在推动海洋经济发展的同时也对海洋环境产生一定的影响。进行海洋发展评价可以及时准确地掌握海洋发展状况，可以为海洋经济发展、海洋资源开发与海洋环境保护提供决策依据，促进海洋经济—资源—环境的协调可持续发展。而客观筛选与构建评价指标体系是进行海洋发展评价的基础与关键，需要相关的理论进行指引；需要在综合考虑社会、经济、资源和环境等多方面的基础上，进行海洋发展评价指标的初步选取，深入探讨指标体系结构的合理性与重要性。

本文首先基于德尔菲法选取了能够突出反映海洋发展评价相关的社会损益指标、经济损益指标、资源损益指标、环境损益指标作为评价指标体系的准则层要素。德尔菲法虽然考虑了专家经验与决策者的意向且不受评价指标数值的影响，但是在赋权筛选过程中会带有主观随意性。为了提高评估分析的客观性，在计算指标权重的过程中，熵权法虽然具有较强的数学理论依据，结果也比较客观，但是不能反映专家的知识、经验以及决策者的意向，而将两种方法结合起来使用，既可充分考虑专家的知识和经验，消除信息熵的负面影响，又可减少赋权中的主观随意性影响，使评价结果更加客观。粗糙集理论利用信息表描述论域中的对象，它是一张二维表，每行描述一个对象，每列描述对象的一个属性。其优势在于不需要任何预备的或额外的有关数据信息，就能有效地分析不精确、不一致、不完整的各类信息，并能通过分析和推理，揭示潜在的规律。运用熵权法结合粗糙集理论为评价指标的进一步筛选约简提供了新方法。

本文指标筛选的局限性主要有两点。一是运用德尔菲法进行海洋发展评价指标的初始化筛选具有一定的人为主观性，这对后续评价指标的客观筛选产生了一定影响。二是熵权法与粗糙集理论相结合进行评价指标筛选约简，如果优先运用粗糙集理论进行第一次约简，然后再运用熵权法进行指标筛选，最终得到的评价指标体系与先使用熵权法再结合粗糙集理论得到的评价指标有些许差异，所以指标约简筛选的方法使用顺序会对最终的评价指标体系产生一定的影响。

虽然关于海洋发展评价的实证案例研究越来越多，但是现阶段仍然未形成统一的海洋发展评价理论框架体系，在基础理论、评价指标、指标体系、评价方法及评价标准等方面仍存在一定的局限，尚未形成相对完善并获得学界一致认同的理论体系，因此海洋发展评价研究仍然存在许多困难。今后的研究方向主要是围绕以下几点完善基本框架体系：指标因子筛选约简→构建指标体系→提出理论方法与模型构建→阈值标准确定→评价结果→影响因素分析→提出建议。

4 结论

目前，海洋发展评价的难点主要体现在评价因子、评价体系、评价模型、评价标准的不确定性以及评价类型的单一化。如何在提升海洋经济高质量发展的同时改变过去无偿使用海洋资源的情况，减少对海洋环境的破坏，已成海洋发展评价过程中所需要关注的重点。本文运用熵权法与粗糙集理论相结合进一步进行指标筛选约简，为海洋发展评价指标体系的筛选构建提供参考，主要结论如下：

第一，运用德尔菲法初步筛选构建了海洋发展评价指标体系，从社会损益、经济损益、资源损益、环境损益4个方面构建准则层；从社会效益、社会成本、经济效益、经济成本、资源效益、资源成本、环境效益、环境成本等8个方面构建要素层；初步筛选出40个评价指标构成因子层。

第二，基于熵权权重大小排序，运用熵权法从40个海洋发展评价指标中进行第一次评价指标约简，从每个要素层中分别独立约简掉一个不重要指标，筛选出32个评价指标，从而构成海洋发展评价指标体系。

第三，基于数据离散化结果，运用粗糙集理论分别计算了8个要素层的分辨矩阵，从32个海洋发展评价指标中进行第二次评价指标约简，最终筛选出24个评价指标从而构成海洋发展评价指标体系，以此作为海洋发展评价的基础。

第四，海洋发展涉及社会、经济、资源、环境、政策等诸多方面，评价指标的筛选、指标权重的确定、安全阈值的计算、评价方法的选择等，都有待进一步探讨和实证。