基于K/N系统和MARS算法的长区段路基边坡稳定可靠性评价
2021-10-21陈伟航王腾飞张文生李政韬
罗 强 陈伟航 王腾飞 张文生 李政韬
(1西南交通大学土木工程学院, 成都 610031)(2西南交通大学高速铁路线路工程教育部重点实验室, 成都 610031)
路基边坡主要由天然岩土材料构成,由于复杂地质作用,在漫长的形成过程中不可避免存在较大变异性[1].Wu等[2]从不确定性角度以随机变量和随机过程为研究对象,用可靠指标β和失效概率Pf评价边坡稳定性.常用方法主要有一次二阶矩法、一次可靠度法、响应面法和蒙特卡洛模拟法(MCS)等[3].MCS在可靠度计算过程中,无需考虑极限状态曲面的复杂性和功能函数的非线性,仅进行足够次数的模拟就可得到较精确的可靠指标β和失效概率Pf[4].影响边坡稳定的因素较多,且分析结果随材料与几何参数呈强非线性变化,为确保失效概率达到所需精度,MCS模拟次数应保证在所需概率水平倒数的10倍左右,特别在失效概率较小时计算量过大[5].
随着计算技术的发展,已开发出一系列用于边坡断面稳定分析的软件[6],可基于MCS方便地计算边坡可靠指标β和失效概率Pf,在科学研究与工程实践中被广泛应用[7-8].但长区段路基边坡的系统可靠水平显著低于断面可靠性,通过控制沿线路纵向离散分布的边坡断面可靠度,进行工程范围内边坡系统整体可靠性评价具有极大风险.因此,对以不连续破坏为主[9]的路基边坡系统可靠性进行评价,需依据反映路基边坡失稳的有限宽度空间特征,将长区段路基边坡划分为N个独立单元分别计算,再基于串联或K/N系统等系统-单元模型进行分析[10].对于铁路和公路等带状线路工程而言,N通常较大,使计算量过于繁重,需消耗极大人力与时间进行重复机械工作.
多元自适应回归样条算法[11](multivariate adaptive regression splines, MARS)为解决上述高维非线性大数据量问题提供了便捷而高效的解决方案,已广泛应用于岩土工程领域[12].MARS可在不设定目标函数形式的前提下,利用小部分样本学习多维影响因素与结果的内在复杂联系,生成更简单、易于解释的显性表达式模型,用于快速预测其余具有相同影响因素的样本结果.
综上所述,本文依据边坡土体变异程度与边坡失稳空间特征的内在关联性,将长区段路基边坡划分为各自独立的单元.为避免大量繁琐的边坡断面可靠度计算,依据土性、几何参数分类,将影响因素相同且个数较多的单元组成总样本集D,抽取少量代表性样本作为训练集Dv,经稳定性计算获取β.基于Dv的参数与结果空间进行自适应学习形成MARS预测模型,快速估计预测集内边坡单元β.
采用系统-单元模型描述长区段路基边坡系统与单元边坡断面可靠度间的关系.串联系统中一处边坡单元的局部失稳将导致系统整体失效,对具有可修复性的路基边坡系统过于严苛.通常在路基结构设计使用年限内,为平衡安全性与经济性,少量边坡单元局部失稳对线路系统长期安全运营产生的风险是可接受的.因此,本文选取具有一定容忍度的K/N(F)[13]系统评价长区段路基边坡系统的可靠性,在N个独立边坡单元组成的系统中,当失稳单元个数大于系统容许失稳个数K时才认为系统失效.
1 路基边坡断面可靠度计算
1.1 边坡独立区段划分
边坡的破坏模式随岩土材料的变异性、几何参数和区段长度的变化而不同.当土体物理力学性质的水平SOF(scale of fluctuation)大于边坡高度且小于边坡长度一半时,沿边坡走向会出现多处宽度有限的不连续破坏[9],如图1所示.一条线路的长度通常可达数十至数百千米,路基边坡高度多在20 m以内,土体水平SOF在10~80 m之间[14],边坡长度与水平SOF的比值较大,因此路基边坡以不连续破坏为主导[10].

图1 路基边坡失稳现场
边坡局部失稳长度可视为有可能存在一个潜在失效事件的最小长度.失稳长度受边坡的几何形状、土体的物理力学性质等影响[15].Lacasse等[16]对加拿大New Liskeard地区No.11新建公路路堤可靠性进行分析,统计发现路堤边坡失稳长度约100 m,如图2(a)所示.2020年法国铁路TGV欧洲东部线位于下莱茵省Strasburg至Vendenheim间发生约55 m长路堑边坡失稳[17],如图2(b)所示.

(a) 路堤失稳长度
工程实践中,一般通过复杂的随机有限元法(RFEM)精确计算边坡局部失稳长度.Hicks等[15]通过RFEM分析黏土边坡(坡高5 m、坡角45°、长500 m)在不同水平SOF下的失稳长度,发现SOF值从12 m增加到100 m时,失稳长度从(13.3±8.0)m增至(47.5±27.3)m,两者呈正相关.
综上分析,路基边坡局部失稳长度与水平SOF有关,一般在100 m以内,基于文献和现场调查的工程失稳案例破坏范围多在30~70 m.为此,本文将路基边坡按50 m均分为若干独立单元进行稳定可靠度计算.
1.2 研究对象及断面统计
研究对象为一段设计标准300 km/h的有砟轨道高速铁路路基,总长约200.1 km,路堤153.2 km,路堑46.9 km,多为山前洪积平原地貌,地形起伏较小,地势平坦开阔;部分区段为构造侵蚀剥蚀中山、丘陵地貌,地形起伏较大,对段内高边坡采用分级设计,平台宽2 m,土质边坡分级高度8 m,岩质边坡分级高度9 m.线路均处于亚热带干旱、半干旱气候地区,干热季节长,年平均气温16.2 ℃;且全年干旱少雨,年平均降雨量为122.8 mm,雨水对边坡的渗流和软化作用微弱,可在可靠性分析中忽略降雨的影响.
考虑路基边坡坡高低于2 m或坡率缓于1∶3时失效概率Pf较低, 路堑边坡坡脚与其同侧路基边沟距离大于坡高2倍时对线路安全威胁较小,这2种情况均不纳入统计.将研究对象按50 m间隔划分,经筛选得到有效路基边坡单元共2 691个,见表1.

表1 有效路基边坡数量统计
1.3 单元稳定可靠度计算方案
线路沿线地形地貌与地质条件的变化导致了路基边坡的复杂性, 在稳定可靠度计算中分为土质和岩质2类边坡.
1.3.1 土质路基边坡
通过二维边坡稳定性分析软件Slide2计算土质路基边坡可靠度,基于均值滑面搜索策略进行MCS计算[18].如图3所示,滑面是半径为R的圆弧,坡高为H,安全系数Fs采用Fellenius法按下式计算:

图3 土质路基边坡Fellenius模型
(1)
式中,Wi、ci、φi、li、αi分别为第i个土条的重力、黏聚力、内摩擦角、底面长度、土条底面与水平面夹角;I为土条总数.
为进行稳定可靠度计算,可设置功能函数Z:
Z=Fs-1
(2)
则可靠指标β可表示为
(3)
式中,μZ和σZ分别为函数Z的均值和方差;μF和σF分别为Fs的均值和方差.
假设Z服从正态分布,则失效概率Pf为
(4)
式中,φ为标准正态分布函数.
研究区段共2 279个单级土质路基边坡单元,占总边坡单元的84.7%,为减少重复性机械工作,建立单级土质路基边坡可靠指标预测MARS模型,提高计算效率.二级土质边坡单元存在台阶且坡率不一致,几何控制参数与单级土质路基边坡差异较大,但数量较少(66个),可直接采用Slide2软件计算.
1.3.2 岩质路基边坡
岩体内部存在许多形态各异的不连续面[19],导致岩质路基边坡失稳模式具有多样性,对应稳定可靠度计算方法亦不同.依据岩体完整性系数Kv、岩石质量指标(rock quality designation, RQD)和岩体风化程度将岩体分为4类:块状结构、层状结构、碎裂结构和散体结构[20].
碎裂结构和散体结构多位于构造破碎带或强风化破碎带,由大小不规则的岩块组成,失效模式与土质路基边坡类似,可按图3所示模型计算.
层状结构可根据岩层倾角与坡面倾角的相对位置进一步划分为层状同向、层状斜向和层状反向结构,其中层状斜向和层状反向结构均有较高稳定性.层状同向结构可根据岩层倾角细分为水平岩层、切层和顺层边坡,顺层边坡稳定性较高.水平岩层和切层边坡的岩层倾向与坡面倾向一致,但岩层倾角缓于坡面倾角,可能发生平面滑动失稳.
通常平面滑动失稳潜滑体的危险滑面为过坡脚的岩层不利结构面,如图4(a)所示.图中,θ为坡面倾角;γ为岩层倾角;Le为滑动面长度;G为坡体自重;Ne为滑动面的法向力;Ts为滑动面的抗滑力.采用RocPlane软件,基于MCS计算岩质边坡平面滑动可靠度.
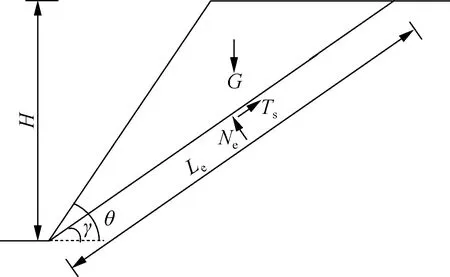
(a) 平面滑动失稳模型示意图
对于块状结构岩质边坡,根据岩层结构面和边坡几何参数判断是否可形成楔形体.节理面和岩层面切割形成的楔形体可沿结构面的交线发生滑动,通常将沿二面交线的滑塌称为楔体失稳,如图4(b)所示.采用Swedge软件,基于MCS分析边坡楔体稳定可靠性.
在346组岩质路堑边坡单元中,层状斜向、层状反向和顺层边坡有288个,其稳定程度较高,失稳风险较低,可不进行可靠度计算.仅有58个边坡可能存在平面滑动或楔体失稳,可靠度分别采用Rocplane或Swedge软件计算.
结合上述分析,对土质和岩质边坡采用不同的边坡断面可靠度计算方案,如图5所示.
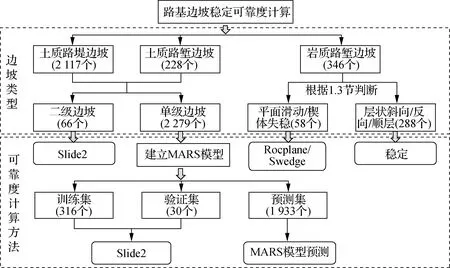
图5 路基边坡稳定可靠度计算方案
2 MARS模型与可靠度预测
针对2 279个单级土质路基边坡单元建立可靠指标预测模型,先结合MARS算法的特点选择训练集样本,再通过Python 3.0中的Py-earth库建立模型,最后评估模型精度并进行预测.
2.1 算法原理
Friedman[11]于1991年提出MARS算法来拟合一组变量与因变量间的关系.该算法作为一种非线性、非参数回归统计方法,通常能高效找出高维复杂数据间的内在规律.MARS算法自适应学习过程可分为2个步骤:
① 向前选择.先将训练集数据分割成不同斜率的线段,这些线段相互之间的连接点称为结点;再在各个结点处逐步搜索基函数(BFs)进行拟合.为了提高模型精度,算法会不断挑选潜在结点并利用BFs拟合,直至达到指定的最大项数.最终形成的MARS预测模型一般可表示为
(5)
式中,f(X)为预测值;β0为常数;J为预设最大基函数个数;βj为第j个基函数的系数,用最小二乘法估计;λj(X)为第j个基函数,可以由单个样条函数或多个样条函数线性组合而成.
为了更加简便,仅将样条函数的形式考虑为分段线性函数,即
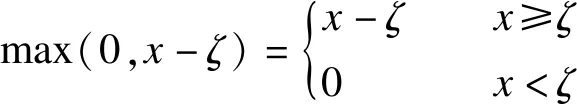
(6)
式中,ζ为x的某一取值,仅当x≥ζ时才有意义.
② 向后剪枝.通过向前选择过程形成的模型通常呈过拟合状态,不利于模型预测训练集外数据.需通过广义交叉验证(GCV)准则,对贡献过小的BFs剪枝,减小模型过拟合几率,也能避免最终预测模型含有过多样条函数.GCV方程[21]可用于检验拟合优度,不断删除BFs直至GCV的值最小时模型最优.GCV方程如下:
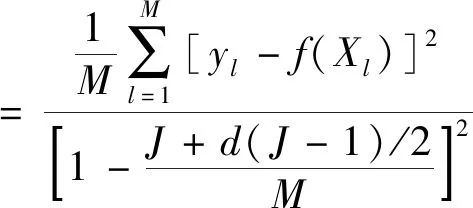
(7)
式中,ϑ为GCV值;yl为第l个对象的输入值;M为数据组数;f(Xl)为模型预测值;d为惩罚参数[11],表示每个BF对应的优化成本,默认为3.
MARS算法可较好地捕捉高维数据的内在复杂关系,并生成更简单、易于解释的模型.该算法具有计算耗时少、可输出显性表达式、有助于在未编程条件下使用等优势,但对超出训练集范围的数据预测精确不高.为保证模型整体预测精度,避免欠拟合,应保证训练集样本全面且不冗余.
2.2 训练集数据选取
单级土质路基边坡稳定可靠度主要受坡高H、土体重度γs、坡度系数m、黏聚力c和内摩擦角φ等参数影响.对于研究区段内的土质路基边坡,γs变化较小,可视为常量,不参与MARS建模;边坡几何参数H和m变异性不大,可视为确定性变量;边坡土体参数c和φ的变异性较大,需按随机变量考虑.综上,选用H、m、μc、μφ、σc、σφ共6个因素进行MARS建模,其中μc、σc分别为c的均值和方差,μφ、σφ分别为φ的均值和方差.
考虑各因素量纲不同,为便于统计,将2 279个土质路基边坡单元的影响因素按下式分别标准化:
(8)
通过MARS预测模型减轻人工重复机械工作量,应尽可能选取较少的典型样本作为训练集,同时确保模型精度足够高.训练集样本在各维影响因素水平上应满足:① 样本数据与真实总体样本分布相近;② 避免预测样本的参数远离训练集参数空间,训练集样本应保证足够大的覆盖范围.
因此,在6维影响因素水平上分别通过分层抽样法[22]采集样本,将总区间[0,1]等分为40份,子区间长度L为0.025.图6为标准化后各影响因素的分布规律.
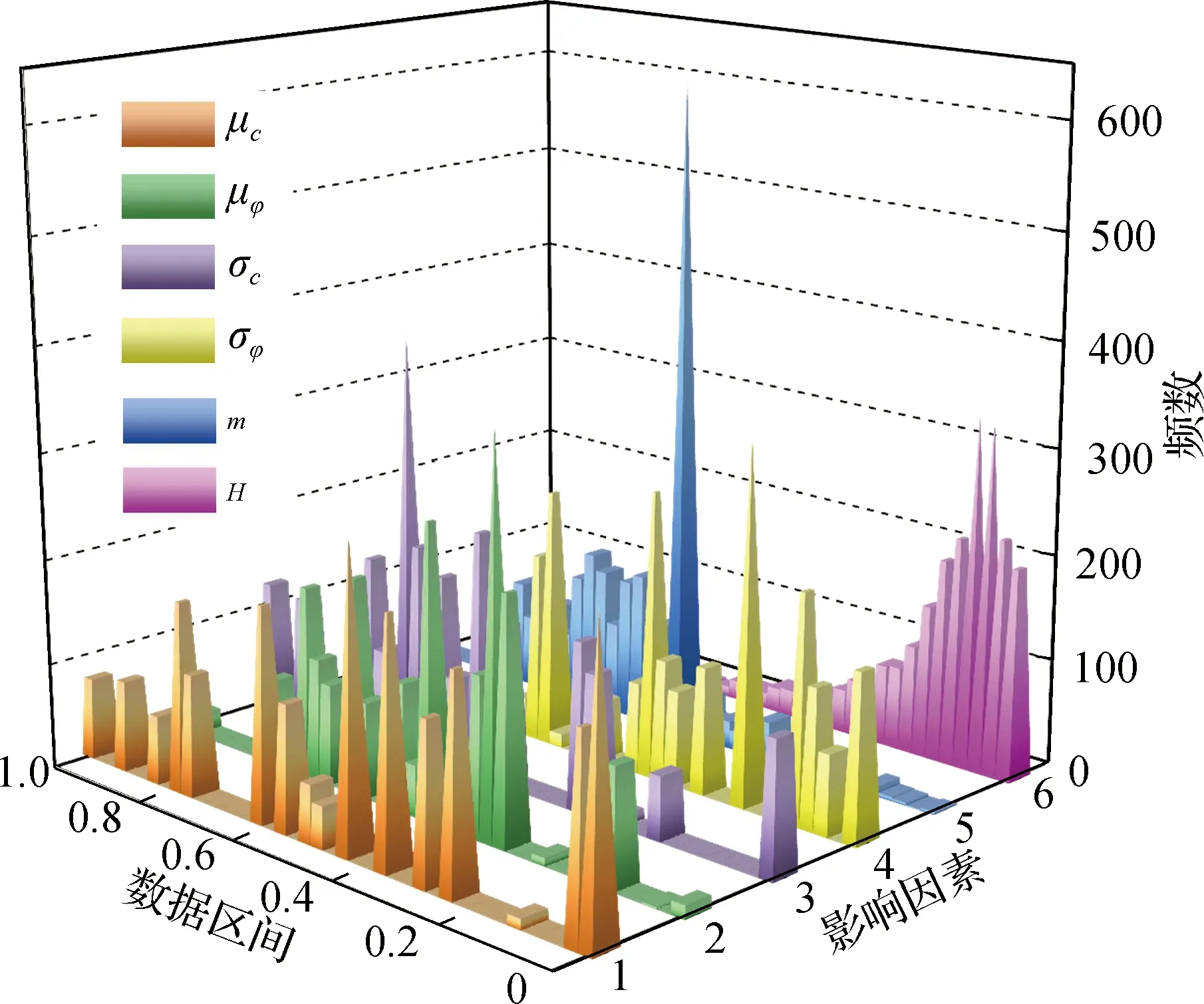
图6 各影响因素的分布

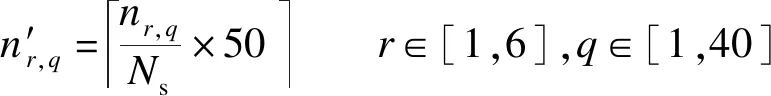
n′r,q=nr,qNs×50 r∈[1,6],q∈[1,40]
(9)
式中,nr,q为不同区间内总样本个数;Ns为单级土质路基边坡样本总数;「⎤为向上取整.将各维影响因素水平上抽取的316个土质单级路基边坡单元样本作为训练集.
图7为标准化后总样本集和训练集样本升序排列热力图,通过对比发现2个样本集趋势类似,说明训练集与总样本集分布接近.这有助于MARS算法在向前选择阶段,有充足的数据来拟合样本点集中区域,保证大部分数据预测精度.总样本集中坡高H超过橘红色、内摩擦角均值μc超过深红色和坡度系数m小于深蓝色的样本很少(见图7黑色框部分).若严格按总样本分布选训练集,会使这3部分数据量过少,降低模型局部预测精度.为避免此问题,通过式(9)在选择样本时强制向上取整,保证训练集数据覆盖范围.从图7(b)中训练集样本H、μc和m分布上可分别观察到橘红色、深红色和深蓝色数据条带变宽.

(a) 总样本集升序分布
训练集样本详细统计信息见表2,为方便使用MARS模型生成的表达式,输入数据均为未经标准化的原始数据.
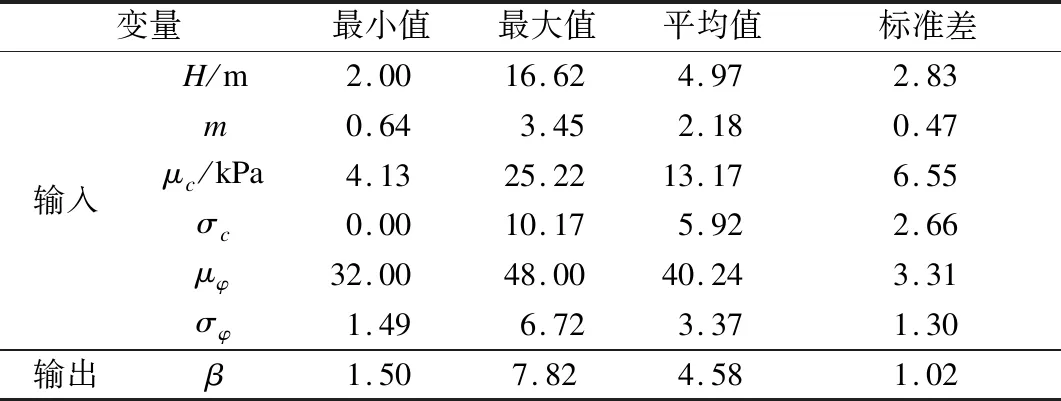
表2 训练集样本统计信息
2.3 模型建立
MARS模型在正向选择阶段,会逐步增加基函数个数形成过拟合模型.在向后剪枝阶段根据模型的GCV值将拟合效果贡献度较小的基函数逐步剪枝,从而找到最优模型.
如图8所示,通过改变模型基函数容许个数o来寻找最佳模型.发现o=29时,模型的GCV值首次达到最小值0.031 3,继续增大o,GCV保持不变,说明o=29时模型最优,基函数个数超过29时,会因过拟合而被逐步剪枝为最优模型.表3为o=29时最优MARS模型的基函数及模型表达式:

表3 最优MARS模型基函数及其表达式

图8 基函数容许个数与GCV值的关系
β′=7.637 7+0.548 6B1-0.276 1B2+0.187 9B3+
0.097 0B4-0.343 4B5+2.887 6B6-1.994 6B7+
0.205 5B8+0.005 6B9-13.784 9B10-0.244 6B11+
0.294 6B12+41.013 6B13-0.014 5B14-0.015 4B15-
0.008 2B16-0.727 5B17+0.367 0B18+0.019 0B19+
0.196 4B20-0.261 0B21-0.026 1B22+0.007 4B23-
0.010 0B24-0.018 2B25-0.008 0B26-0.036 7B27+
0.021 5B28-0.881 3B29
(10)
式中,B1~B29为MARS算法在向前-向后选择过程中,依据GCV值所选择的影响因素交互项.
2.4 可靠度预测与评价
使用29个基函数的最优MARS模型进行评价与预测.训练集样本可靠指标计算值β在1.505~7.818之间,平均值为4.582,标准差为1.019;训练集样本可靠指标预测值β′在1.501~7.815之间,平均值为4.582,标准差为1.010.两者的平均值相同,且标准差相差极小,说明预测值与计算值整体相近.统计可靠度指标计算值与预测值的相对误差,结果如图9所示,可看出相对误差在±6%以内的样本占94.94%,仅极少数样本相对误差超过±10%.
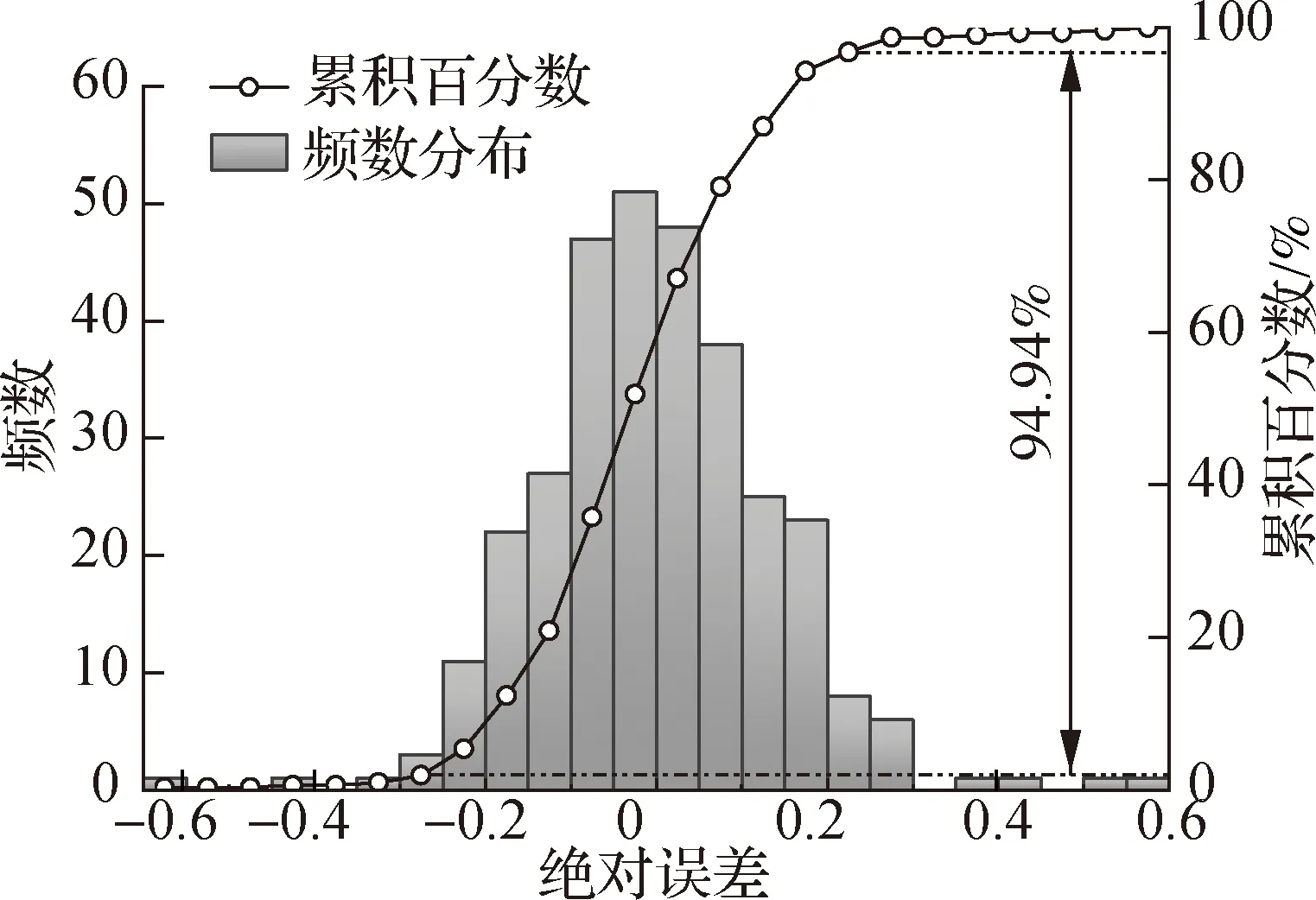
图9 预测结果相对误差分布
通过均方根误差(RMSE)、平均绝对误差(MAE)、决定系数R2评价模型的整体性能[23-24].
如图10所示,训练集样本绝大部分数据在±10%误差范围内,最大误差不超过16.5%,且RMSE仅为0.135 8,MAE仅为0.102 5,说明预测数据整体稳定,偏差很小.R2高达0.982 3,说明MARS模型可以很好地表达各影响因素与可靠指标间的内在复杂联系.

图10 可靠度指标计算值与预测值对比
为验证MARS模型的预测精度,从训练集外样本中随机抽取30组数据作为验证集进行预测,具体输入参数与预测结果见表4.如图10所示,验证集数据均在±10%的误差范围内,且RMSE仅为0.156 0,MAE仅为0.132 5,R2高达0.974 0.因此,MARS模型能够较好地预测可靠指标,具有较高的可信度和准确性.
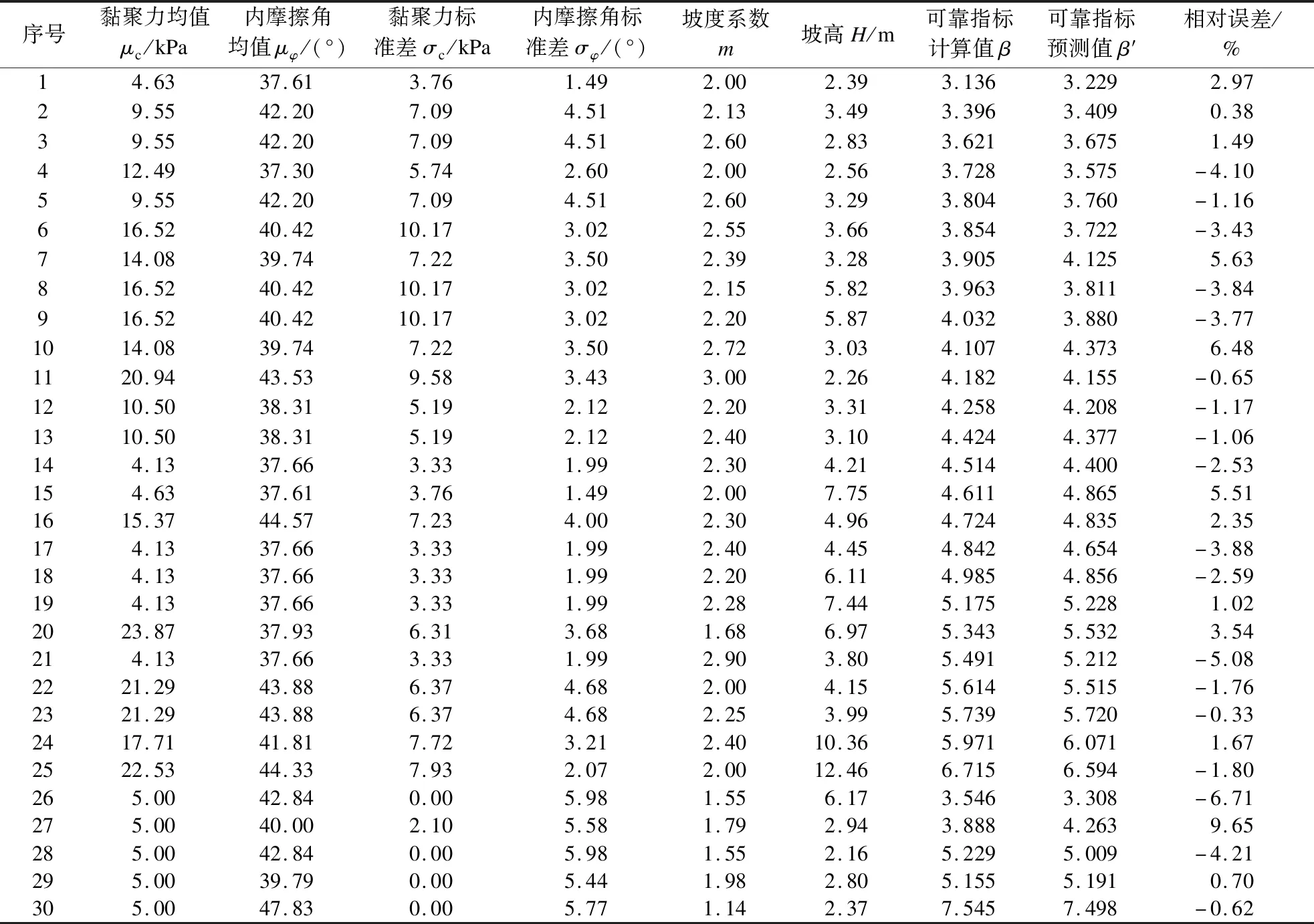
表4 验证集样本输入参数与结果对比
3 长区段路基边坡系统可靠性评价
3.1 K/N系统可靠度计算
将整个长区段路基边坡视为大量边坡单元组成的系统,单个边坡单元可靠度与系统可靠度之间的关系可用K/N(F)系统进行描述,如图11所示.当N个单元中至多有K个元件失稳时, 即失稳的单元数小于等于K时, 系统正常工作, 反之系统失效.

图11 长区段路基边坡K/N(F)系统(单位:m)
用失稳边坡单元个数Nf除以系统总边坡单元个数N来表示系统失效率ξ[13],即
(11)
则系统累积失稳个数Nfa为
Nfa=⎣Nξa」
(12)
式中,ξa为系统累积失效率;⎣」为向下取整.
各个边坡单元的稳定性是独立的,有t(t≤Nfa)个边坡失稳时的系统失效概率PfsT为
(13)

当系统累积失稳边坡个数Nfa=K时,系统累积发生概率为
(14)
此时,对应的系统失效概率Pfs为
Pfs=1-PNfa
(15)
3.2 边坡系统可靠性评价
使用训练好的MARS模型计算预测集内1 933个单级土质路基边坡单元的可靠指标β,根据式(4)求解对应失效概率Pf.统计研究区段内2 691个路基边坡的Pf,如表5所示,将其组集为K/N(F)系统,进行路基边坡系统可靠度计算.

表5 系统各单元失效概率频数分布
《铁路建设工程风险管理技术规范》(Q/CR 9006—2014) 依据发生概率P将风险事件划分为5级:频繁发生(P>30%)、可能发生(3% 图12 系统失效概率随失效个数变化规律 可以发现, 2个和3个边坡单元失效的概率分别为37.311%和31.193%,属于频繁发生的风险事件;1、4和5个边坡单元失效的概率分别为11.320%、13.978%和3.909%,为可能发生的风险事件;1个边坡都不发生失稳的概率为0.959%,仅会偶然发生.因此系统不发生破坏的可能性很小,且大概率会破坏2~3个边坡. 利用式(15)分别计算系统累积失效边坡个数Nfa=K时的系统失效概率Pfs,结果如图12所示.K≤2时,Pfs≥50.410%,为频繁发生事件;K=3,4时,Pfs分别为19.217%、5.239%,为可能发生事件;K=5时,Pfs=1.330%,属于偶然发生事件.发现K>4时,Pfs≤3%,因此研究区段路基边坡失稳累积个数不超过4个(占总单元数的比例为0.149%)的置信度大于97%. 对于相同研究区段,路基边坡单元长度取25和100 m时,可划分边坡单元总数分别为5 382和1 346个,相应失稳累积个数不超过7和2个的置信度大于97%,分别占各自总边坡单元数量的0.130%和0.149%.可以看出,97%置信度水平对应系统容许累积失稳边坡单元个数虽不同,但失效个数占总边坡单元数量的比例差异较小,说明单元长度取值对路基边坡系统稳定可靠性评价无本质影响. 1) 针对路基边坡失稳的有限宽度空间特征,将长区段路基边坡沿纵向划分为彼此相邻的独立单元,基于K/N(F)系统分析边坡系统可靠度与单元边坡失稳概率的关系,提出一种长区段路基边坡稳定可靠性评价方法. 2) 边坡系统可靠度分析存在多断面重复运算问题,通过MARS算法建立单元边坡几何、材料属性六维参数与可靠指标β的内在联系,形成以29项基函数表达的高精度非线性预测方程,大幅提高了众多单元边坡可靠度的计算效率. 3) 采用可容忍一定数量单元边坡失稳的K/N(F)系统,实现长区段路基边坡局部失稳单元个数与系统失效概率的量化评价,建立边坡失稳累积个数(或占比)与系统风险等级的关系.研究区段路基单元长度按50 m划分时,最可能发生2~3个边坡失稳,概率分别为37.3%、31.2%;边坡累积失稳个数占比不超过0.167%的置信度大于97%. 4) 路基边坡局部失稳长度在合理范围内取不同值时,系统独立边坡单元数量随之变化,进而影响系统失效概率随失效个数的分布特征,但按单元失效个数占比评价系统失效概率时分布趋于一致.本文方法无法评估可能失稳边坡单元的空间分布,而边坡单元连续或间隔失效对系统造成的灾害严重程度显然不同,后续将针对此问题进一步开展研究.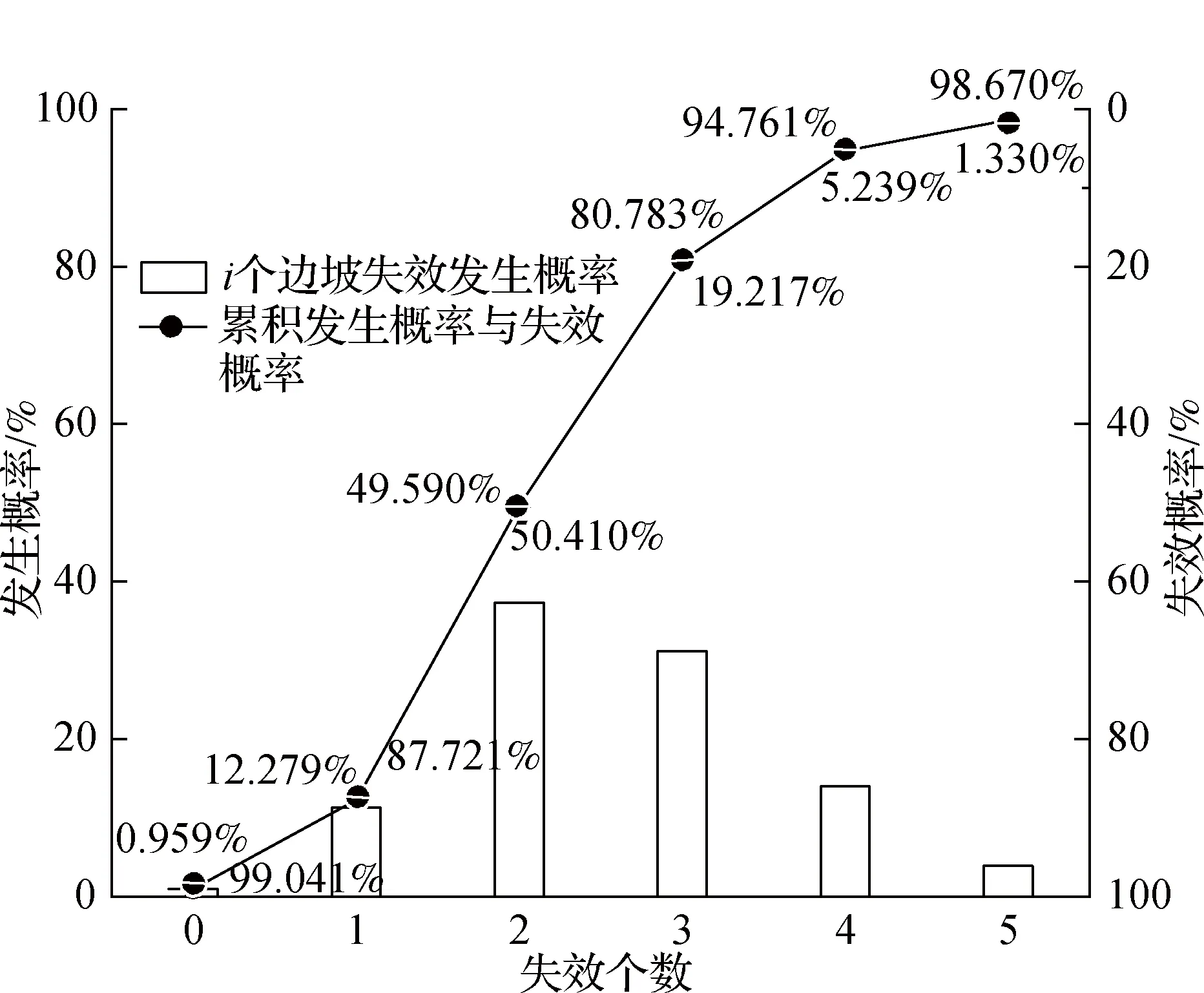
4 结论
