椭圆形无内环索网结构受力性能分析

鲁 建 薛素铎 李雄彦

(北京工业大学建筑工程学院， 北京 100124)

张拉结构具有质量轻盈、造型美观、跨越能力强、施工周期短等优点，广泛应用于实际工程中[1-3].目前，张拉结构主要包括索穹顶结构[4-6]、轮辐式结构[7-8]、无内环空间索桁结构[1-3,9]、索网结构[10]、索承网壳结构[11]等形式.部分张拉结构需要强大的内环索作为连接所有径向索的转力构件，以便构成中间大开口，方便采光和通风；部分张拉结构则需要强大的环索连接径向分布的平面索桁架以增加结构的侧向稳定性.文献[5,8,11]表明，张拉结构的关键构件环索会导致用钢量较大，当环索破断时，结构将丧失承载能力，甚至发生连续性倒塌事故.为解决张拉结构所面临的问题，需要在已有结构形式的基础上提出新的结构体系.

文献[12]提出了无环索预应力索支结构新体系，包括无内环索桁张拉结构[1-2]、单层无内环交叉索网结构[10]和无环索预应力索承网壳结构[11]等.文献[1-3]中的结构主要由上下层交叉索网、压杆和受压环梁组成；文献[10]中的结构主要由单层索网和受压环梁组成，形成自平衡体系；将文献[1-3]中结构的上弦索变成网壳，便可形成文献[11]中的无环索预应力索承网壳结构.无环索结构体系摒弃了内环索，以相互交叉一起的索网形成一个虚拟内环，而虚拟内环的每段索与其余内环索段没有直接关系，当虚拟内环索中的任一段断开后，不影响其他索段受力，故而提高了抗连续倒塌能力.

本文针对体育项目的特点和张拉整体结构内环索失效或破断问题，在文献[10]的基础上，提出了一种椭圆形无内环索网结构.二次开发了该结构的建模和找形软件，并对其进行了静力分析、参数化分析和断索研究.

1 建模及找形的二次开发

椭圆形无内环索网结构的平面形状由椭圆方程控制，单层索网的稳定性由马鞍形曲面所形成的正反双曲面提供,马鞍形曲面的曲率由其矢跨比控制.椭圆形无内环索网结构控制方程为

(1)

式中，R1、R2分别为椭圆的长轴半径和短轴半径；h为马鞍曲面外环的最大矢高；η为马鞍曲面矢跨比.

基于ANSYS有限元软件的APDL语言，二次开发了椭圆形无内环索网结构的参数化建模软件，实现了各种跨度、环向等分数N1、单索所跨越的环向等分数N2、马鞍曲面矢跨比η、整体预应力水平β等控制参数下的参数化建模功能.椭圆形无内环索网结构的结构形式见图1.

(a) 平面投影图

基于非线性有限元理论对该结构进行找形时，可对索施加初应变或赋予负温度，使索网结构产生预应力以抵抗外荷载作用.基于APDL语言和式(1)，二次开发了椭圆形无内环索网结构的参数化建模及找形软件.找形步骤如下：

①根据结构模型尺寸，输入相关控制参数R1、R2、N1、N2、η，得到结构的几何模型；

②对几何模型进行网格划分，得到相应结构的有限元模型；

③对有限元模型施加较大初应变或负温度，并设置小弹性模量；

④利用Newton-Raphson法，设置大变形命令、应力刚化命令及收敛容差，进行迭代求解；

⑤恢复材料的真实初应变和弹性模量，并再次进行迭代求解；

⑥更新节点坐标，直到前后2次计算结果满足收敛容差(一般位移及应力收敛容差取0.001)，迭代结束.

2 静力性能分析

椭圆形无内环索网结构三维模型示意图见图2.长轴单元编号为L1～L6，短轴单元编号为S1～S6.平面投影中R1=30 m，R2=20 m，N1=18，N2=6，η=3/R1.索体直径为45 mm，其横截面面积为 1 196.17 mm2，钢丝强度为1 520 MPa，破断索拉力为1 818.178 kN，弹性模量为133 GPa，泊松比为0.3，温度膨胀系数为1.2×10-5.不考虑环梁变形对结构的影响，在有限元软件中将环梁约束设置为刚性连接.

图2 椭圆形无内环索网结构三维有限元模型

对索网结构施加的初始应变为0.005，初应力为665 MPa，应力比为0.38，未超过规范[13]中容许应力比0.5.根据找形程序对结构进行找形，结果见图3.

图3 椭圆形无内环索网结构找形结果

由图3可知，索网结构的主要应力分布范围为524.41～777.14 MPa，与初始应力650 MPa基本相符，索网应力分布范围较为均匀.迭代完成前的最后2次迭代计算的变形容差较小，满足工程要求，最终找形后的最大变形为0.022 m.

设施加到结构上的外荷载为1.0 kPa，其等效节点荷载为F.研究分级荷载为0.4F、0.6F、0.8F、1.0F、1.2F、1.4F时，满跨荷载及半跨荷载对结构的影响.由于该结构的平面投影为椭圆形，存在2个方向的强轴和弱轴，故可将半跨荷载分为第1类半跨荷载和第2类半跨荷载(见图4).

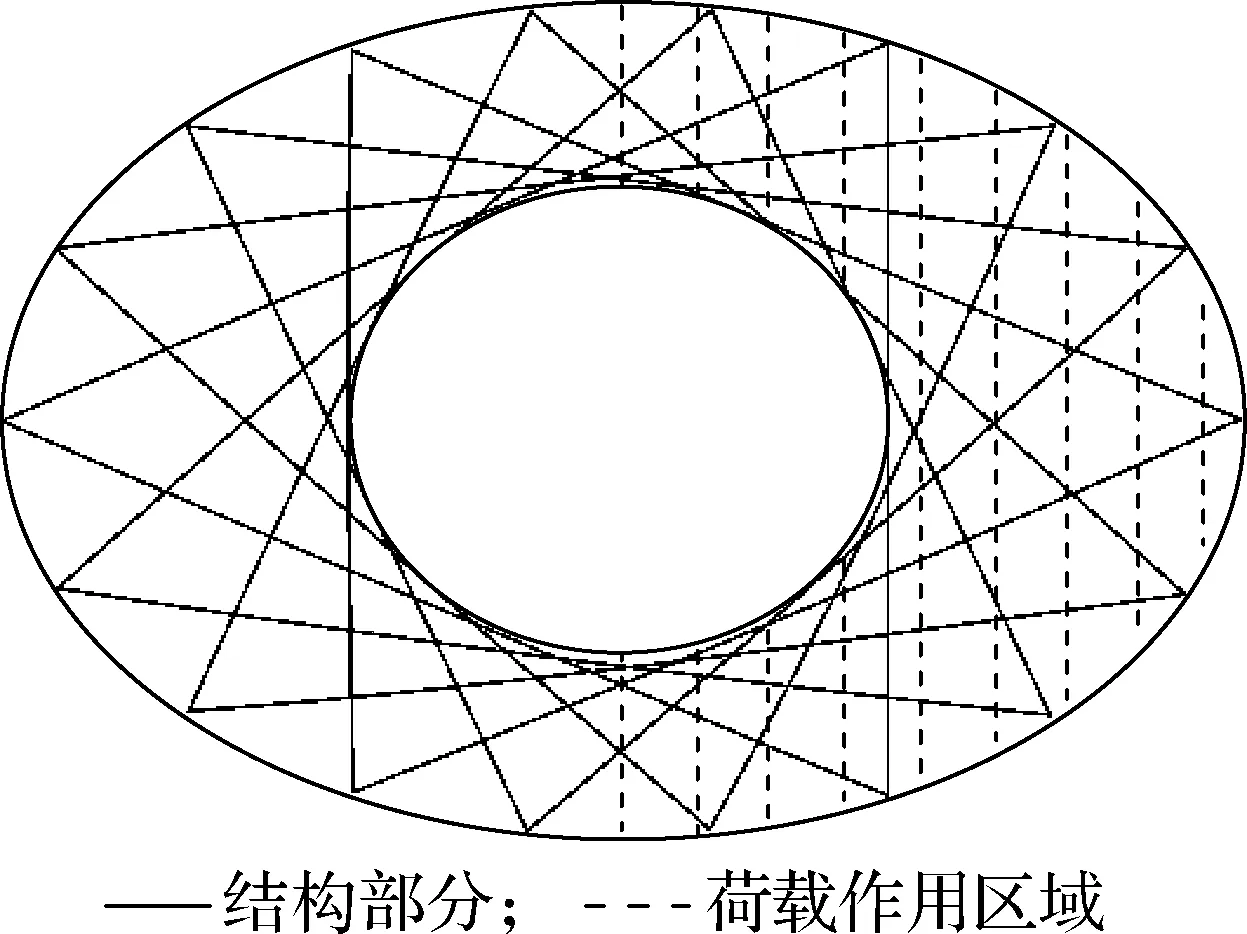
(a) 第1类半跨荷载

在满跨、半跨荷载作用下，当荷载为0.4F～1.4F时，荷载与结构内力和位移的关系曲线见图5.

(a) 位移-荷载关系曲线

由图5(a)可知，随着荷载F的增加，索网结构位移线性增大.当荷载为1.2F时，满跨荷载、第1类半跨荷载及第2类半跨荷载对应的索网结构最大位移分别为0.168、0.169、0.164 m，均满足《索结构技术规程》(JGJ 257—2012)[13]容许位移值σ=min(R1/200,R2/200)=0.2 m.在第1类半跨荷载作用下结构的最大位移值最大，因此在实际工程设计中需要验算第1类半跨荷载对结构的影响.

由图5(b)～(c)可知，随着荷载的增加，索网结构的最大应力线性增大，最小应力线性减小.在3类荷载作用下，第2类半跨荷载引起索网结构的最大、最小应力值均最大，因此在实际工程设计中需要验算第2类半跨荷载对结构最大内力的影响.当荷载为1.4F时，满跨荷载、第1类半跨荷载及第2类半跨荷载对应的索网结构最大应力分别为890.774、874.883、917.052 MPa，最大内力分别为 1 065.52、1 009.54、1 096.95 kN，均满足已知索的强度限值要求.满、半跨荷载分析结果表明，弹性范围内时，荷载与结构响应呈线性关系，半跨荷载对结构最为不利，实际设计过程中不可忽视.

表1给出了荷载作用下相邻单元内力值.由表可知，无荷载作用下，索力为661.63～979.98 kN；有荷载作用时，索力为549.82～1 041.20 kN.虽然整体结构的内力分布范围稍大，但相邻单元的索力分布相差不大.

表1 外荷载作用下相邻单元内力值 kN

分析时选取长轴方向的水平风荷载(简称风荷载1)、短轴方向的水平风荷载(简称风荷载2)以及竖向风荷载或风吸力(简称风荷载3).这3种风荷载、恒载及温度组合作用对结构的影响见表2.由于降温对结构有利，升温对结构不利，故研究升温20 ℃对结构的影响.

表2 不同荷载组合下结构的最大响应

由表2可知，在10种组合下，恒载、活载与升温组合对结构竖直向下位移最不利，风荷载3与升温组合对结构竖直向上位移最不利，风吸力对结构内力最不利.故实际设计时，选择恒载、活载与升温组合作为控制结构竖直向下位移的荷载组合，选择风荷载3与升温组合作为控制结构竖直向上位移的荷载组合，选择风荷载3作为控制结构内力的荷载取值.

3 参数化分析

参数化分析时，不考虑受压环梁对结构的影响，在有限元软件中将环梁约束设置为刚性连接.

3.1 环向等分数

通过设置不同的环向等分数，分析其对结构的影响，结果见表3.由表可知，随着N1的增加，最大位移Dmax逐渐减小，且减小趋势明显.这是因为N1增加时虽然施加给索网的初应变相同，即索网应力S的分布范围大致相同，但单索的数量增加，索网密度增大，故结构刚度增大，结构位移减小；同时，结构的最大应力Smax基本不变，而最小应力Smin增大，且S逐渐缩小.当N2不变时，N1越大则中间开口面积A1越大，悬挑部分面积越小.

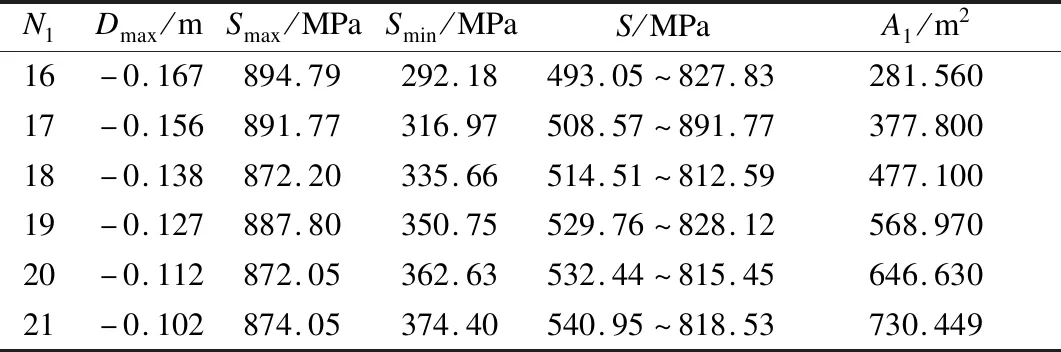
表3 环向等分数对结构的影响

由此可知，增加N1可增加结构的刚度，减小Dmax，同时也增大了用钢量.故实际工程中，在满足相关规范要求的最大位移限值基础上，应尽量减少单索数量.

3.2 单索跨越的环向等分数

通过设置不同的单索跨越的环向等分数，分析其对结构的影响，结果见表4.由表可知，随着N2的增加，结构位移先增大，然后逐渐减小，中间开口面积减小，而结构的最大应力变化不大，最小应力减小，索网应力分布范围先减小后变大.究其原因在于，N2增大时索的数量及初应力均没有改变，但单索长度增加，索网密度变小，即刚度减小，故结构位移增加.当N1不变时，N2越大，中间开口面积越小，悬挑部分面积越大，且随着N2的增大，悬挑面积增加越明显.

表4 单索跨越的环向等分数对结构的影响

由此可知，应根据实际结构跨度来设置N2，从而得到合理的结构刚度和开口面积.

3.3 马鞍曲面矢跨比

通过设置不同的马鞍形曲面矢跨比，分析其对结构的影响，结果见表5.由表可知，随着η的增大，结构的最大位移逐渐减小且位于虚拟内环处.当η=0.017时，最大位移为-0.313 m；当η=0.083 时，最大位移为-0.098 m.同时，索网应力分布范围上限基本保持不变，下限逐渐减小.由此说明，在其他控制参数不变的情况下，增大η能够显著提高结构刚度，但在一定程度上会导致索力分布不均匀.

表5 马鞍曲面矢跨比对结构的影响

3.4 椭圆形状

当R2=20 m时，通过设置不同的R1，分析椭圆形状对结构的影响，结果见表6.由表可知，随着R1/R2逐渐增大，结构的Dmax逐渐增大且均位于短轴方向的虚拟内环处，而索网应力分布范围基本保持不变.究其原因在于，R1增大时结构总面积的增幅较大，中间开口面积的增幅较小，即索网覆盖面积逐渐增大(见图6).而单索的总数量保持不变，索网结构的密度逐渐减小，故结构刚度减小，最大位移增大.由于短轴方向的索网密度小于长轴方向的索网密度，最大位移位于短轴处，当R2=72 m时，最大位移为-0.23 m，已超出短轴方向的位移限值0.2 m，但未超出长轴方向的位移限值0.3 m.因此，在实际工程中，R1/R2应控制在合理范围内，若超出R1/R2的合理范围则需要增大N1或N2.

图6 结构面积与椭圆长半轴的关系

3.5 预应力

通过设置不同的预应力，分析其对结构的影响，结果见图7.由图可知，在弹性范围内，预应力增大时，最大位移逐渐减小，且两者呈线性关系.由此表明，提高预应力可有效提高索网结构的刚度，降低结构的最大位移值.

(a) 预应力-位移曲线

3.6 弹性模量

常用拉索弹性模量为100～165 GPa.通过设置不同的拉索弹性模量E，分析其对结构的影响，结果见表7.由表可知，随着拉索弹性模量的增加，索网结构的最大位移逐渐减小，最大、最小应力逐渐增大.由此表明，弹性模量对结构内力和位移影响较大，工程设计中应进行弹性模量的材性试验，以确定真实弹性模量.

表7 弹性模量对结构的影响

3.7 索截面面积

通过设置不同的索截面面积A，分析其对结构的影响，结果见表8.随着索截面面积的逐渐增大，结构的最大位移逐渐减小.在弹性范围内，位移与索截面面积呈线性变化，应力分布范围基本保持不变.因此，实际设计时应选择合理的索截面面积，以节约材料.

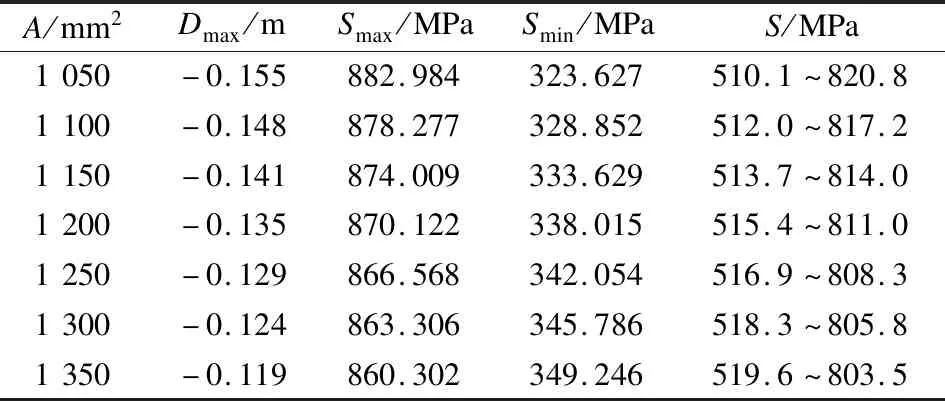
表8 索截面面积对结构的影响

4 断索分析

椭圆形无内环索网结构中索与索之间无直接相关性，断开任何一根索并不影响其余索的传力路径，即结构具有较好的抗倒塌能力.由第3节中的算例结果可知，该结构包含强轴和弱轴，故研究长、短轴方向的索单元断开后对结构的影响.

利用ANSYS软件中瞬态动力学模块对索进行瞬时移除，同时考虑结构的大变形和预应力效应，求解断索后的结构响应.根据图2中单元L1～L6和S1～S6的位置，求得外荷载为1.0 kPa时结构位移及内力响应，结果见表9.由表可知，单元L1和S1的失效比对结构位移的影响大于其余索失效对结构的影响，断索后结构的最大位移为-0.693 m，在可接受的范围内，且结构最大响应位置均在断索处，索网结构的最大内力均小于索的最小破断索力1 818.178 kN.断开单元L5时，索网的最大内力位于临近单元L5处，其值为1 150.82 kN.断索对结构位移和内力的影响范围接近，且断索后的变形仅影响与断索处相邻近的构件(见图8).由此可知，该结构不存在敏感性构件，各构件的内力基本相当，索网结构受力较为均匀.

表9 断索对结构的影响

(a) 内力最大位置

5 结论

1)基于ANSYS有限元软件的APDL语言，二次开发了椭圆形无内环索网结构的参数化建模与找形分析软件.

2)静力分析结果表明，半跨荷载对结构更不利，且恒载、活载与升温组合作用对竖直向上的位移最不利，风荷载3与升温组合作用对竖直向下的位移最不利，风吸力对结构内力最不利.

3)参数化分析结果表明，增加环向等分数、改变马鞍曲面的矢跨比、提高索网结构的预应力水平及增大索的截面面积均可增加结构刚度，减小结构最大位移.单索所跨越的环向等分数及结构的长、短轴比值应控制在合理范围内，且弹性模量对结构的影响较大.

4)断索分析结果表明，该结构不存在敏感性构件，抗断索能力较好，索网结构受力较为均匀.