逆向思维在初中数学解题中的应用

纪红芳

(江苏省南通市通州区金郊初级中学 226300)

思维模式主要有两种：一种是正向思维，即根据现成的资源，正向推进，稳扎稳打，逐步发展；一种是逆向思维，即倒推资源配置，从目标出发逆向而行，借助已知条件逐步推进.初中数学是一门基础学科，涵盖面广，逻辑性强，在学习过程中常常会碰到一些难题，在用正向思维难以解决的时候，不妨引导学生采用逆向思维来“夺取胜利”.本文通过例析逆向思维在初中数学解题中的应用，谈谈在教学实践中一些具体做法.

一、逆向推导

学习平方差公式是通过多项式的乘法进行计算正向推导得出结论，如果解题时采用逆向推导的方法去运用公式，可以激发出学生的学习兴趣心，促进课堂教学的顺利开展.

例1简便计算5512-4492

师：请大家观察这条算式的特点，联系学过的公式，看看是不是能利用公式来计算呢？

生：我想到了平方差公式：(a+b)(a-b)=a2-b2.(教师板书公式)

师：你的思维很活跃.我们一起来观察这条平方差公式具有哪些特征.

生1：等式左边是两个二项式相乘，这两个二项式中的第一项完全相同，第二项互为相反数.

生2：右边是两项的平方差，也就是相同项的平方与相反项的平方的差.

师：把这条公式反过来就是a2-b2=(a+b)(a-b)(教师板书公式)

师：你能用一句话把这条公式解释一下吗？

生：求两项的平方差就等于求这两项的和与这两项的差的积.

师：再来看算式5512-4492，这里的两项分别是指什么？

生：数字551和数字449.

师：5012-4992可以分解为哪两个因式的积？

生：可以分解为(551+449)与(551-449)的积.

师：现在你能把这道题非常简便地计算出来吗？

生：能.5512-4492=(551+449)×(551-449)=2000.

师：从运用平方差公式进行来简便计算的过程中，你得到了什么启发？

生：把平方差公式逆向思考，就得出了“两个数的平方差等于这两个数的和与这两个数的差的积”的结论，这样计算起来就非常简便.

这个课例中，教师引导学生逆向思考平方差公式，透过深入分析其内涵，深化了学生的理解与记忆.

二、逆向计算

学生计算题目时，往往会按部就班，根据常规的计算法则进行运算.实际上，数学中的许多计算法则都具有可逆性，在解题的时候教师就要充分利用这种可逆性，引导学生恰当运用公式法则寻求题目的简捷解法.

师：你准备怎么计算这道题？

师：大家觉得这种方法可行吗？

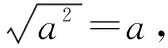
生：太方便了，而且很容易计算到正确的结果.

如果按照常规方法无法解决的时候，应该及时转换思路，尝试采用逆向思维的方法去解题，即由题目中所给条件的可逆性，思考逆转后会出现什么情况，能否再回到原来的题目中，如果可行的话，那就大胆地另辟蹊径去解决问题.

三、逆向分析

有些数学题，从已知条件直接入手去思考，会得到多个结论，导致在解题过程中“迷失方向”，不知道该如何继续下去.此时如果逆向分析，从题目的结论出发，逐步往回逆推，往往可以找到满意的解题途径.

例4已知x、y是不相等的正数，求证：x3+y3>x2y+xy2.

师：观察这条不等式，你想到了什么解题思路？

生：我看到不等式左边是x3+y3，马上就想到了公式：x2+y2=(x+y)(x2-xy+y2)，我就想能不能用这条等式来解题呢？

师：先请大家把不等式两边分解因式.

生：x2+y2=(x+y)(x2-xy+y2)，x2y+xy2=xy(x+y).

师：题目中要求证的不等式就转化为(x+y)(x2-xy+y2)>xy(x+y)，仔细观察，要使这道不等式成立，只需知道什么条件？

生：转化后的不等式两边都有因式(x+y)，因为x和y都是正数，x+y>0，所以只需知道x2-xy+y2>xy就可以了.

师：你真爱动脑筋！我们再用这样的思路去逆向分析题目.

生1：把不等式的右边项移到左边，转化为x2-2xy+y2>0，即求出(x-y)2>0就可以了.

生2：因为x、y是不相等的正数，所以(x-y)2>0是成立的.

这个课例中，学生采用“顺推不行则逆推”的方法进行逆向思考，打破了解题思路中的僵局，结合已学知识顺利地迎来了“新局面”.如果经常进行此类习题的练习，学生的创造性思维将会有飞跃的进步.

四、逆向证明

反证法因其遵循“由果溯因”的思维模式在学习某些基本的性质、定理和结论中经常被运用，因此在教学时教师也要将此作为解题的重要方法，引导学生在解决难度较大的题目时有意识地去尝试运用.

例5勾股定理的证明

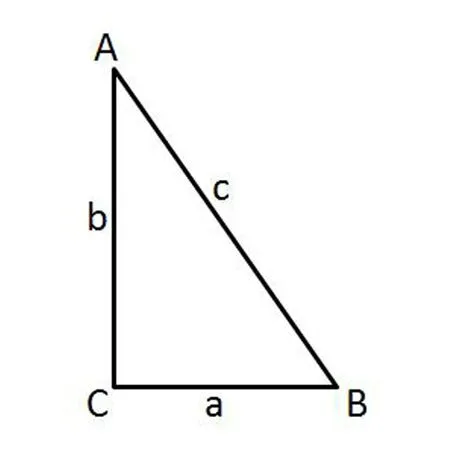
师：如图1，在Rt△ABC中，∠C=90°，三个边长分别为a、b、c，求证：a2+b2=c2.

师：可以用量出AB、AC、BC的长度后直接计算的方法来证明吗？

生：当然不行.

师：那怎么来求证两条直角边的平方和等于斜边的平方呢？

生：试一试用反证法.

师：好办法.说说你的思路.

生：假设a2+b2≠c2.

师：即BC2+AC2≠AB2.

生：如图2过C点作斜边AB上的垂线，垂足为O.

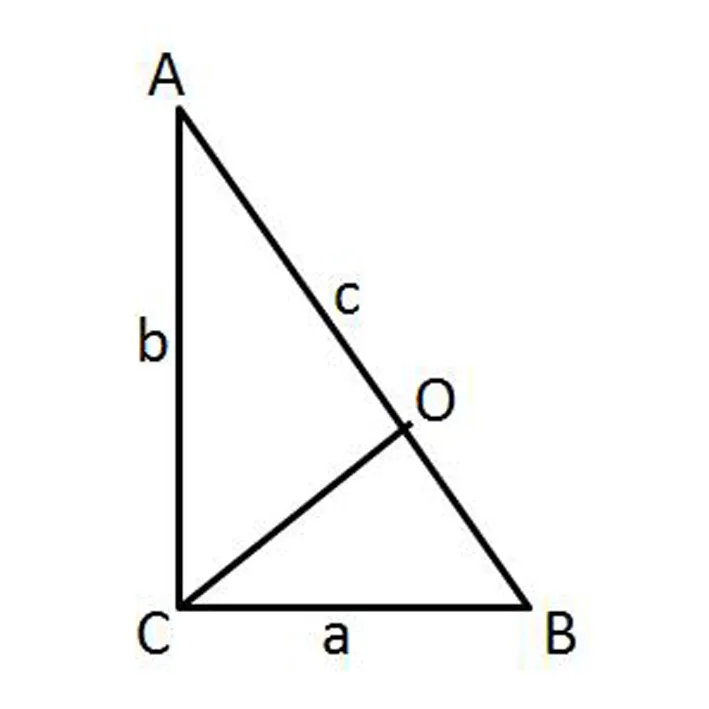
(教师在图形上添加辅助线CO)

生：斜边AB被分为两条线段AO和OB，由AB2=AB·AB=AB(AO+BO)=AB·AO+AB·BO

师：为什么要考虑这一步呢？

生：根据刚才的假设，可以推测出：BC2≠AB·BO，AC2≠AB·AO，即BO：BC≠BC：AB，或者AO：AC≠AC：AB.

师：可以看出BO和BC是Rt△BOC中的一条直角边和一条斜边；AO和AC是Rt△AOC中的一条直角边和一条斜边.

生：在△AOC和△ACB中，因为∠A=∠A，则当AO：AC≠AC：AB时，∠AOC≠∠ACB；在△BOC和△BCA中，因为∠B=∠B，则当BO：BC≠BC：AB时，∠BOC≠∠ACB，又因为∠ACB=90°，所以∠AOC≠90°，∠BOC≠90°，这与添加的辅助线CO⊥AB相矛盾，所以BC2+AC2≠AB2不成立.

师：你利用反证法证明出了AC2+BC2=AB2，即a2+b2=c2.

从这个课例中可以看出，反证法从假设命题结论的反面入手，将相反的判断作为已知条件，经过严谨的逻辑推导出与已知题设条件相矛盾的结论，从而证明原命题成立.