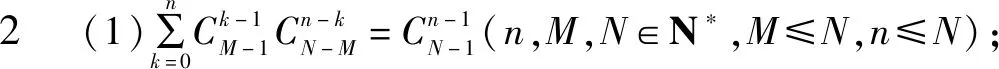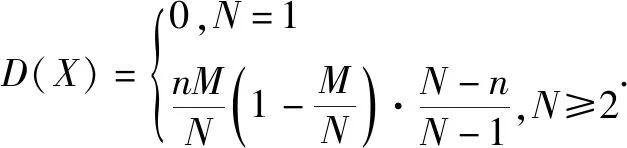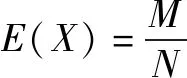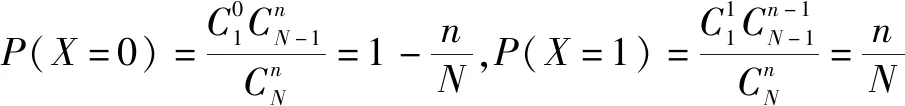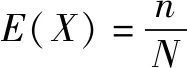超几何分布的分布列、期望与方差

甘志国

(北京丰台二中 100071)

普通高中课程标准实验教科书《数学·选修2-3·A版》(人民教育出版社，2009年第3版)(下简称《选修2-3》)第48页给出了

超几何分布的定义1 一般地，在含有M件次品的N件产品中任取n件，其中恰有X件次品，则

即

其中m=min{M,n}，且n≤N,M≤N，n,M,N∈N*.

如果随机变量X的分布列具有表1的形式，则称随机变量X服从超几何分布.

表1

高等学校统计教材[1]第98页及《数学词典》第463页给出的超几何分布定义(且该词条里等式右边分母中的“k”应改为“n”；所给方差公式也不完整，完整的方差公式可见后文定理3)也均同超几何分布的定义1.

拙文[3]指出了以上定义中的“随机变量X的取值范围是{0,1,…,m}”不对，并将其修正为

超几何分布的定义2 在含有M件次品的N件产品中，抽取n件产品(其中n≤N,M≤N；n,M,N∈N*).设其中恰有X件次品，则称随机变量X服从的概率分布是超几何分布.其分布列有以下两种情形：

(1)当n≤N-M时，X的分布列为

(2)当n>N-M时，X的分布列为

最近出版的高中数学教材普通高中教科书《数学·选择性必修·第三册·A版》(人民教育出版社，2020)(下简称《选择性必修·第三册》)第77-78页给出了超几何分布定义，即

超几何分布的定义2-1 一般地，假设一批产品共有N件，其中有M件次品.从这N件产品中不放回的随机抽取n件，用X表示抽取的n件产品中的次品数，则X的分布列为

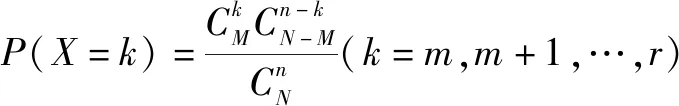
其中n,M,N∈N*，M≤N,n≤N,m=max{0,n+M-N},r=min{n,M}.如果随机变量X的分布列具有上式的形式，那么称随机变量X服从超几何分布.

显然，该定义与超几何分布的定义2是等价的.

《选择性必修·第三册》第79页还证得了

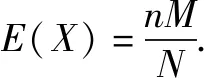
证明令m=max{0,n+M-N},r=min{n,M} ②

由随机变量期望的定义，可得

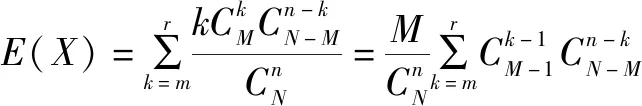
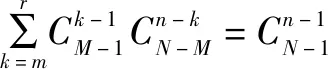
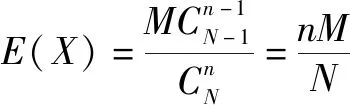
《选择性必修·第三册》配套使用的《教师教学用书》(人民教育出版社，2020)第91页写道：

关于分布列中k的取值范围max{0,n+M-N}≤k≤min{n,M}，可以通过几个特殊例子归纳得出.例如，设10个球中有4个红球、6个白球，如果随机摸出5个球，那么其中红球个数的可能取值为0,1,2,3,4；如果随机摸出8个球，那么其中红球个数的可能取值为2,3,4.

笔者认为这样不妥，难以让学生信服.

实际上，容易理解超几何分布的定义2(它与超几何分布的定义2′等价)，再由其两种情形可得该结论.

建议老师讲述超几何分布的定义2′时，先归纳出超几何分布的定义2，再归纳出超几何分布的定义2′.

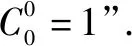
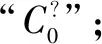
(4)证明定理1的关键就是证明等式④.

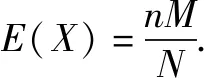
证明实际上，拙文[3]用分类讨论的方法已给出了定理2的严谨证明，再改述如下.

在前面“质疑及解决办法”的(2)中已证得当M=N时成立.

当M=1,N≥2时也成立：因为X的分布列为

表2

下证当N>M≥2即M-1,N-M,N-1∈N*时也成立.

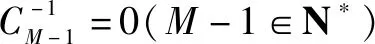
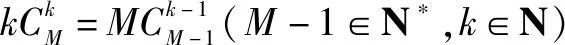
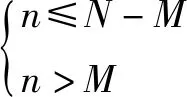
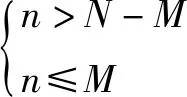
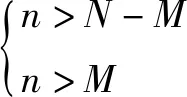
下面只证情形(1)即证⑥(其余的情形均同理可证)：

由恒等式

(1+x)M-1(1+x)N-M=(1+x)N-1(M-1,N-M,N-1∈N*)

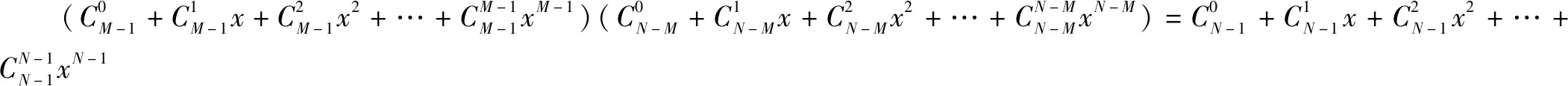
两边的展开式中含xn-1项的系数相等可得.

也可这样来证⑥：

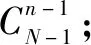
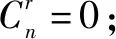
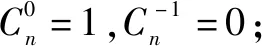
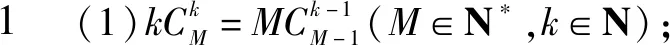
证明由广义组合数的定义，可得

(1)当k>M或k=0时，可得欲证等式的两边均为0；当1≤k=M时，可得欲证等式的两边均为k；当1≤k

综上所述，可得欲证结论成立.

(2)当N=1(即N=n=1)时，可得欲证等式的两边均为1；当N≥2时，可得欲证结论成立.

(3)同(2)可证.

证明当N=1时，可得M=n=1，进而可得D(X)=0.

下证当N≥2时成立.

(1)当n=1时.

①若M=N，可得D(X)=0.

②若M

表3

进而可得当n=1时欲证结论成立.

所以随机变量X的分布列为

表4

进而可得当n=1时欲证结论成立.

(3)当M≥2,n≥2时，令②成立，由广义组合数的定义可得随机变量X的方差

综上所述，可得欲证结论成立.

注也可不用广义组合数的定义按定理2的第一种证法分四种情形来证明定理3.