材料参数变异性对堆渣体沉降变形影响的数值模拟研究
2021-10-21车南雪
车南雪
(河北省子牙河务中心,河北 衡水 053000)
1 研究背景
水资源短缺和时空分布不均已经成为制约我国经济社会发展的重要因素。为了解决这一问题,加大水利工程建设力度就成为重要的工程技术措施。显然,在水利工程建设过程中,一般需要进行大量的土石方开挖,并产生数量巨大的弃渣。弃渣场作为弃渣的集中堆放地就成为水利工程建设的重要配套设施,需要占用大量的土地资源[1]。弃渣场堆积体的坡度越大,其占地面积越小,就可以产生明显的经济效益和生态环境效益[2]。当然,弃渣一般是由比较松散的碎石和土体构成,因此,弃渣堆积体的边坡具有非饱和、欠密实和多孔隙的特点,稳定性差,容易发生滑坡、泥石流等地质灾害,并产生严重的经济损失和社会影响[3]。辽宁蒲石河抽水蓄能电站是我国东北地区兴建的最大抽水蓄能电站,根据工程设计和施工场地特点,需要进行数量巨大的土石方开挖。为了堆放施工弃渣,工程项目部在上水库库盆、下水库库盆、六道坎和泉眼沟等地方设置了四处渣场。其中,设计堆渣量最大的是六道坎渣场,预计其堆渣量将达到34.56万m3,属于大型渣场,研究堆渣体的稳定性具有十分重要的意义[4]。
随着计算机技术的迅速发展,数值模拟已经成为边坡稳定性研究的重要方法,得到了十分广泛的应用。显然,数值模拟计算结果的科学性和准确性会受到多种因素,特别是弃渣材料参数的影响。另一方面,对弃渣堆积体边坡而言,沉降变形又是边坡变形破坏的重要表征参数,对研究弃渣体边坡的稳定性具有重要意义[5]。基于此,本研究以六道坎渣场弃渣堆积体边坡为例,利用数值模拟的方法研究材料参数的变异性对堆渣体沉降变形影响,以期为相关研究和具体的工程设计提供一定的理论借鉴。
2 ABAQUS模型的构建
2.1 计算模型的构建
ABAQUS是一套功能强大的工程模拟有限元软件,其解决问题的范围由相对简单的线性分析逐步拓展到复杂的非线性问题领域。同时,该软件还可以根据不同的模型参数对模型进行调整,而不必重新进行计算模型的构建,对此次研究十分有利。因此,选择ABAQUS软件进行计算模型的构建。
根据工程渣土场的实际勘测资料,设置二维有限元计算模型的长度为82.78 m,总坡高为45 m。对构建的几何模型采用CPE4P网格单元划分[6],该单元为四节点平面应变四边形单元,具有双线性位移和双线性孔压,将各边统一为步种,最终划分为5827个计算单元,4464个计算节点。
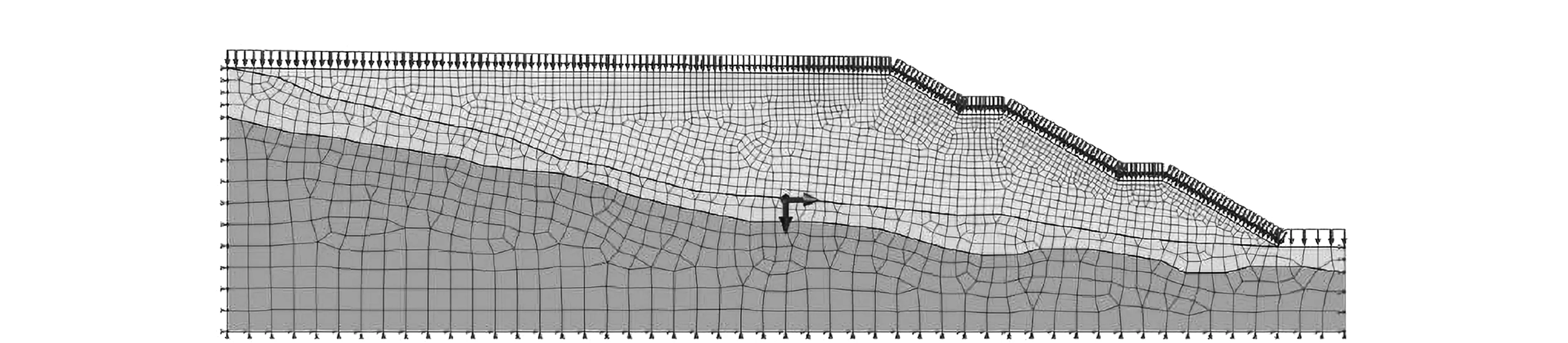
图1 有限元模型示意图
在ABAQUS中提供了邓肯模型、摩尔-库伦模型等多种土体本构模型,由于摩尔-库伦模型能够有效凸显其抗剪强度的不同,更为贴近渣土材料的屈服特征,因此研究中选择摩尔-库伦模型[7]。为了简化计算模型和考虑计算的效率,仅考虑渣土材料的物理力学性质,其容重为23 kN/m3,泊松比为0.28,黏聚力为22.2 MPa,内摩擦角为27.1°,弹性模量为382 MPa。
2.2 边界条件和计算荷载
结合工程的实际情况,对构建的各个表面施加如下边界条件:对模型的两侧施加水平位移约束;对模型的底部施加竖向和水平位移约束[8]。除了施加位移约束之外,在模型的各边界还需要施加荷载,以准确反映边坡的初始应力状态。在荷载施加之后,需要对模型进行初始地应力平衡。首先需要建立静力分析步,将时间设置为10 h,然后在Load模块中对分析区域施加10 kN的重力荷载,从而计算构建的模型在重力作用下的应力应变情况,最终完成地应力平衡。
2.3 计算方案
相关研究结果显示,堆渣体边坡的竖向位移变形是影响其稳定性的重要表征量。因此,研究中利用构建的有限元模型对不同计算方案下的边坡竖向位移量进行模拟计算,以获取模型参数变异系数对边坡稳定性的影响。结合背景工程的实际情况以及模型参数的特点,研究中保持渣土体材料的容重和泊松比不变,选择黏聚力、内摩擦角以及弹性模量作为变异参数进行研究。为了表示参数的变异性,对每种参数均设置了0.2、0.4、0.6、0.8和1.0等5个不同的变异系数,利用构建的模型对不同变异系数下的边坡竖向位移进行模拟计算,根据计算结果,探讨参数变异性对竖向位移的影响。
3 计算结果与分析
3.1 弹性模量
利用构建的有限元模型,对不同弹性模量变异系数下的堆渣体边坡竖向位移进行模拟计算,从计算结果中提取典型高程部位的竖向位移值计算结果,绘制出如图2所示的不同弹性模量变异系数下的竖向位移变化曲线。由图2可知,在不同的变异系数下,堆渣体边坡下部的竖向位移值基本相同,说明材料参数的变异性对边坡底部的竖向位移影响不大。究其原因,边坡底部受岩石地基的约束作用较强,竖向位移的变化并不明显。不同变异系数下沉降位移最大值和变化速率的计算结果如表1所示。由表1中的计算结果可知,当变异系数较小时,其变异性对沉降变形的影响较小,随着变异系数的增大,沉降值的变化速率也逐渐增大。例如,当变异系数为0.2时,竖向位移的变化速率为5.99%,当变异系数为1.0时,竖向位移的变化速率增加到15.34%。

图2 不同弹性模型变异系数竖向位移变化曲线
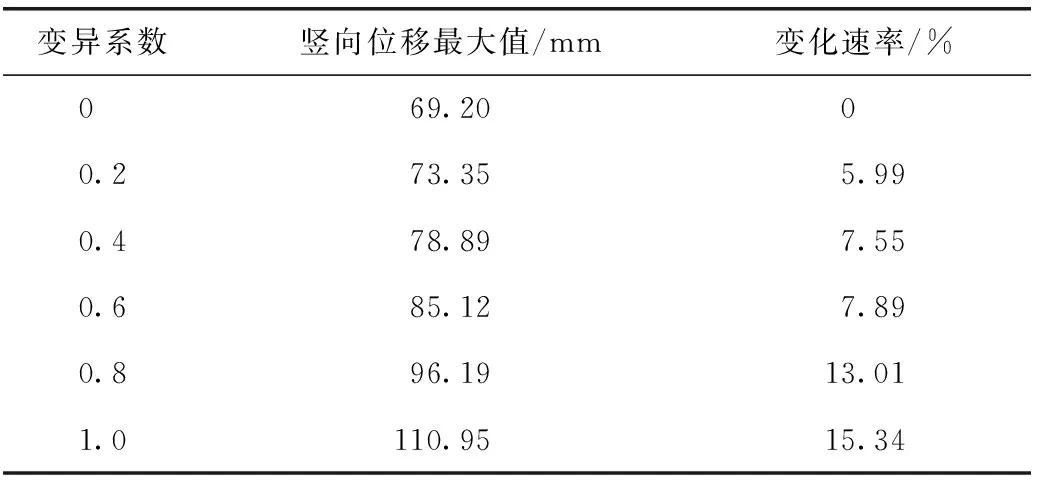
表1 不同弹性模量变异系数竖向位移最大值及变化速率
3.2 内摩擦角
利用构建的有限元模型,对不同内摩擦角变异系数下的堆渣体边坡竖向位移进行模拟计算,从计算结果中提取典型高程部位的竖向位移值计算结果,绘制出如图3所示的不同内摩擦角变异系数下的竖向位移变化曲线。由图2可知,在不同的变异系数下,堆渣体边坡下部的竖向位移值的变化特征与弹性模量相似,变异系数对边坡底部竖向位移的影响较小,对边坡中上部的影响相对较大。不同变异系数下沉降位移最大值和变化速率的计算结果如表2所示。由表2中的计算结果可知,变异系数越大,对边坡竖向位移的影响也越大。例如,当变异系数为0.2时,竖向位移的变化速率为3.01%,当变异系数为1.0时,竖向位移的变化速率增加到12.50%。此外,与弹性模量的计算结果相比,在相同变异系数条件下,内摩擦角的变异性对边坡竖向位移的影响相对较小。例如,在弹性模量变异系数为1.0时,竖向位移的变化速率为15.34%,在内摩擦角变异系数为1.0时,竖向位移的变化速率为12.50%。由此可见,竖向位移对内摩擦角的敏感性相对较低。

表2 不同内摩擦角变异系数竖向位移最大值及变化速率
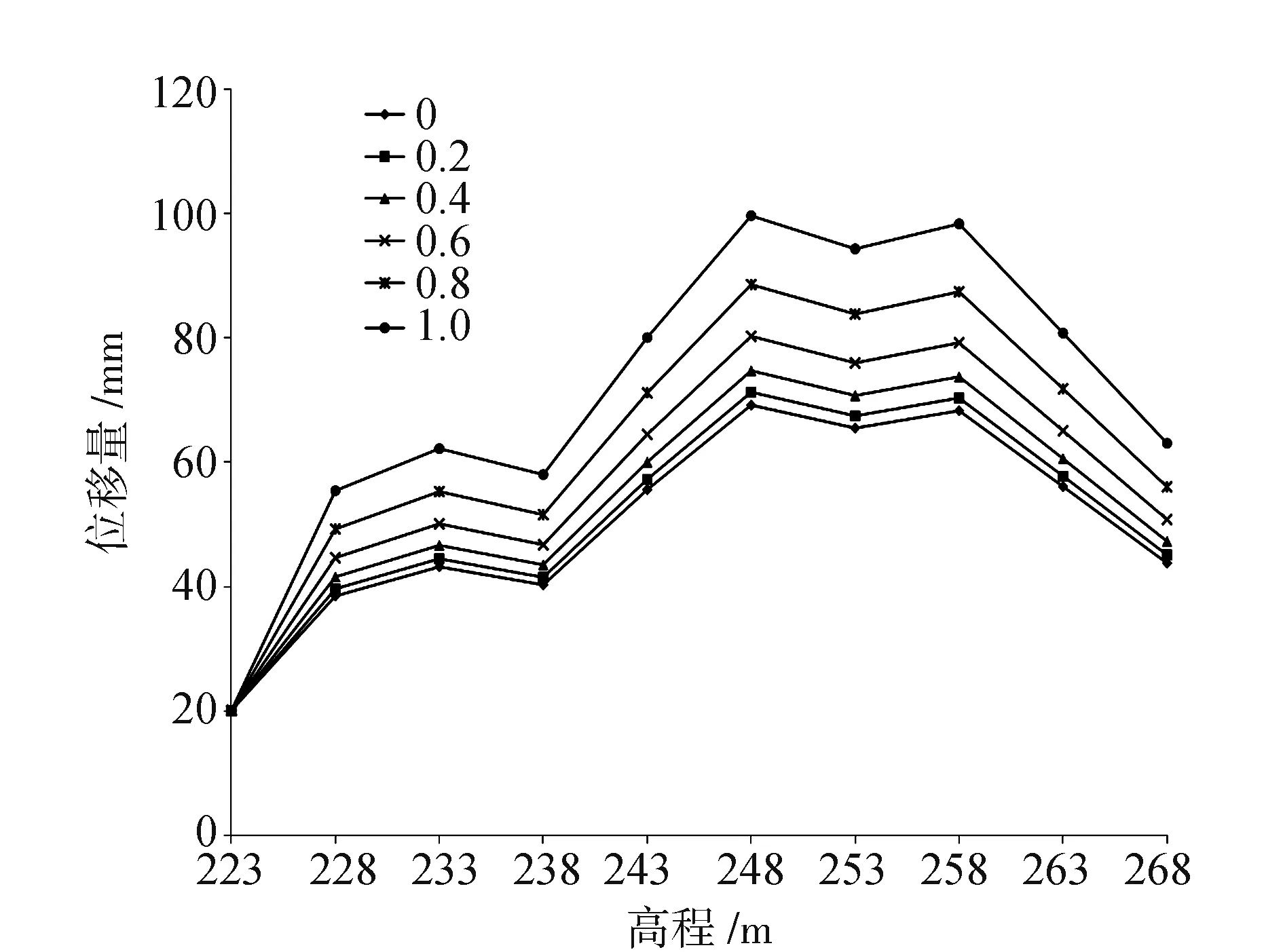
图3 不同内摩擦角变异系数竖向位移变化曲线
3.3 黏聚力
利用构建的有限元模型,对不同黏聚力变异系数下的堆渣体边坡竖向位移进行模拟计算,从计算结果中提取典型高程部位的竖向位移值计算结果,绘制出如图4所示的不同黏聚力变异系数下的竖向位移变化曲线。由图4可知,在不同的变异系数下,堆渣体边坡下部的竖向位移值的变化特征与内摩擦角和弹性模量相似,变异系数对边坡底部竖向位移的影响较小,对边坡中上部的影响相对较大。不同变异系数下沉降位移最大值和变化速率的计算结果如表3所示。由表3中的计算结果可知,与内摩擦角和弹性模量类似,变异系数越大对边坡竖向位移的影响也越大。此外,与弹性模量和内摩擦角的计算结果相比,在相同变异系数条件下,黏聚力的变异性对边坡竖向位移的影响相对较小,三个变量中竖向位移对黏聚力的敏感性最低。

图4 不同黏聚力变异系数竖向位移变化曲线
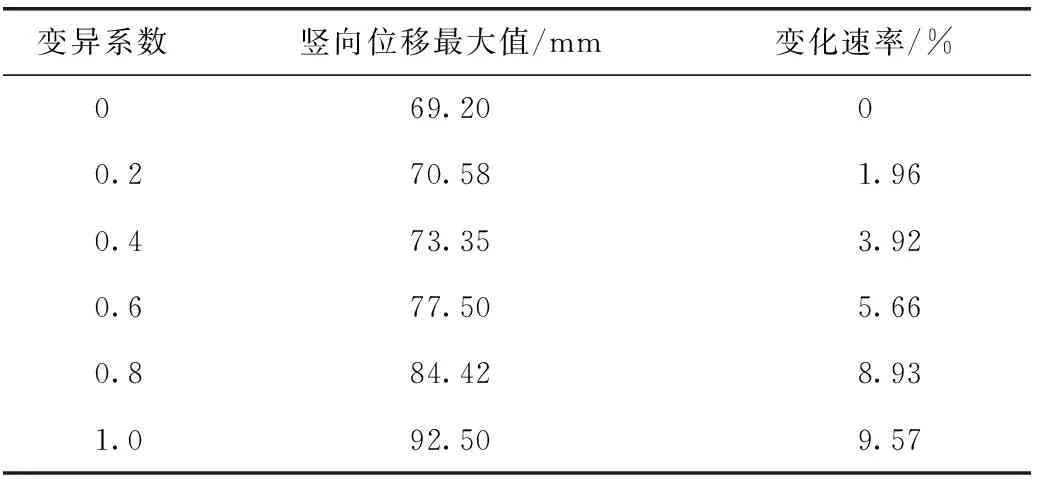
表3 不同黏聚力变异系数竖向位移最大值及变化速率
4 结 论
(1)材料的弹性模量、黏聚力和内摩擦角的变异性对堆渣体边坡下部的竖向位移值影响不大,对中部和上部的位移影响较为显著。
(2)材料参数的变异系数越大,边坡竖向位移的变化速率越快,说明材料参数的变异性越大,对边坡竖向位移的影响也越大。
(3)从弹性模量、黏聚力和内摩擦角对竖向位移的影响对比来看,弹性模量的影响最大,内摩擦角次之,黏聚力的影响最小。
