基于Matlab的工业炉径向热管稳态数学模型构建

黄阿娜

(咸阳职业技术学院，陕西 咸阳 712000)

现阶段，面向径向热管的模拟研究一般都是以CFD模拟Fluent多相流模型进行的[1]，Fadhl模拟探析了以R134a与R404a作为工质的热虹吸管管壁液膜特性；Rahimi通过水作为工质进行了模拟分析，结果表明,在加热功率处于300～350 W不断增加时，热虹吸管效率则会随之提升；涂福炳则在此基础上模拟研究了基于水作为工质的径向热管内部温度场与速度场分布[2]。基于以上研究结果，本文基于Matlab构建了工业炉径向热管稳态数学模型。

1 实验设计

1.1 实验装置

实验系统装置[3]具体如图1所示，其由热管加热、冷却水冷却、数据采集、测量等子模块共同构成。

图1 实验系统装置示意图

其中加热模块基于加热炉与调压-稳压器控制器组成，均匀缠绕加热丝于炉内热管外壁，且利用调压稳压进行加热通断适度调整。同时，在加热丝的外层包裹上保温层，两个侧端以盖扣法兰为辅助加以封闭处理，以此避免加热时发生热损，造成漏热。

冷却模块由冷却水冲刷内管与水流控制阀共同构成，基于严格控制送入内管冷却的水流量，从而实现热量传输。在热管正常开始运行之后，外壁不会出现太过明显的温度变化，此时可断定为热管已处于稳定运行态势，然后基于数据采集仪全方位记录外壁以及进出口冷却水的温度值，同时以电子流量计和温度测量计为载体进行出口流量与冷却水进出口温度测量。热管数据采集仪可自动全面采集温度测量结果相关数据信息，且基于电脑终端加以呈现，以此实现数据输出。

本文径向热管以三种不同工况条件开展实验测量，并适度调整电压大小，以便于有效控制径向热管输入功率，工况条件与输入功率[4]具体如表1所示。

表1 工况及输入功率

1.2 热管模型

以同轴径向热管为模型，直径小，可用热管出口位置径向截面代替整个热管换热情况。热管材料为铜，内部工质与热交换介质为水。径向热管截面[5]具体如图2所示。

图2 径向热管截面

2 稳态数学模型构建

基于热阻与管内工质稳态换热模型融合水于管内定压汽化的相关原理，对热管内传热影响要素进行详细分析，以计算获得在不同条件状态下传热过程的均温分布与最大换热量。

以既定输入功率为基础，工业炉径向热管可实现运行稳定，热量由外管到内管传输需通过7个步骤[6]，具体如图3所示，传热步骤热阻网络关系具体如图4所示。

图3 热管传热过程

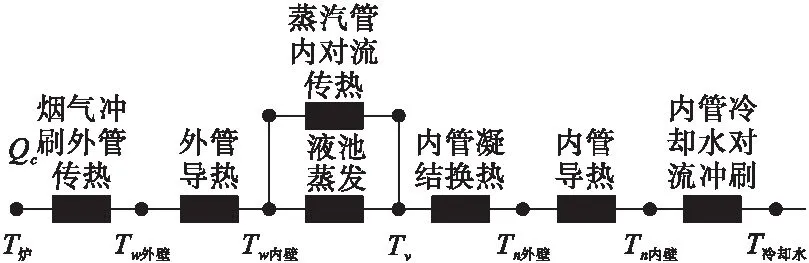
图4 热管传热热阻

蒸汽与液池共同构成了工业炉径向热管内腔，而液池蒸发和套管内蒸汽对流传热同步完成，步骤3与4之间保持并联关系状态。受热阻作用，管内温度沿着径向走向逐步下降。

2.1 冷凝段模型构建

根据数值平板凝结计算模型，进一步推导分析得出沿着径向热管内管壁液膜凝结换热系数的具体分布形态。为精确模拟不同工况状态下水平单管的冷凝模型，假设入口位置为饱和蒸汽，温度为TS，在达到稳定运行状态之后，蒸汽便以避免为载体逐步凝结，以生成稳定层流液膜，在表面剪切力和重力双重作用下，液膜朝向内管底端涌动。

简化冷凝段相关数学模型，需紧紧围绕其关键要素[7]，进行假设：假设液膜温度呈现为线性分布状态，热量以导热为基础以径向加以传输；假设直接忽视液膜的内惯性力；假设以液膜凝结为稳态条件，忽视表层相间波动现象；假设气液相界面并不存在温度差，也就是界面位置液膜温度属于饱和蒸汽温度；假设液膜具备常物性；假设直接忽略液膜的过冷度；假设圆管的外壁一直保持于恒温态势。

就内管管壁为辅助获取液膜的微元体，据此深入探索液膜的具体受力运动流程[8]，具体如图5所示。

图5 液膜受力运动过程

以极坐标为主要方式，R为半径，θ为圆心角，基于此，取δ、dθ沿着管周方向的微元体，其单位为1。在重力超过压强梯度力时，直接忽略摩擦阻力，以简化相关方程，有

质量守恒：

(1)

质量守恒：

(2)

边界条件：

(3)

基于此，冷凝液膜速度与温度分布计算即

(4)

(5)

就质量守恒与能量守恒，获取液膜厚度公式，即

(6)

以牛顿冷却公式为辅助，可知单管壁面的局部凝结换热系数为

(7)

针对上式计算积分，以获得热管冷凝侧对流换热系数，即

(8)

以此冷凝热阻便是凝结换热热阻和气液界面热阻之和，即

(9)

式中：An=πd1le为内管外壁面积，m2；RW为气液界面热阻，K/W；ρ1为水密度，kg/m3；μ1为水动力黏度，Pa·s；λ1为液体导热系数，W/m·K；d为内管直径，m；r为汽化潜热，J/kg；TS为蒸汽饱和温度，K；TW为内管壁温度，K。

2.2 蒸发段模型构建

(10)

则

(11)

2.3 热平衡计算分析

在具体实验时，假设感应加热机的输入电压是380 V，内部安装的电流表精确度数值各不相一，那么加热输入功率计算具体为

Qe=IU

(12)

式中：Qe为蒸发段输入功率，W；I为电流，A；U为电压，V。

输出功率计算即

Qc=cl×ml×(Tlin-Tlout)

(13)

此程序可忽略能量损失，在后续就具体模型，可考虑热力损失系数η。热管温度关系式即

(14)

3 实验结果讨论与分析

所谓数值模拟以1.81 m热管长度为条件，热管处于稳态运行状况时，程序及时将工况、操作、热管结构准确输入，则实时输出相关参数。

数值模拟输入参数需切实依据热管不同状态下的具体稳定运行状况[10]。基于不同冷却水流速状态时，基于输入功率的冷却水出口温度具体如表2所示。

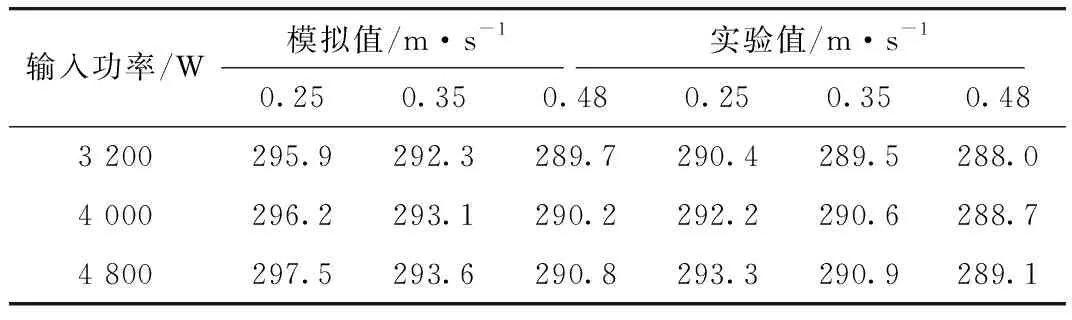
表2 基于输入功率的冷却水出口温度 ℃

由表2可知，工业炉炉内输入功率越大，则实验与模拟的水出口温度越大，而且在水流量越大时，冷却水出口的温度则越低；数值模拟和实验测试所得的冷却水出口温度分布态势高度类似，在流速比较大时，实验测量中的冷却水热管内表面比摩阻随之增大，对实际对流换热过程造成了直接性影响，而流量比较大时，实验与模拟差异明显超过了流量小时的差异。此外，在实验过程中，还需对热量消耗与测量误差的影响性进行综合考虑，因此相对于模拟值，实验值整体偏小，温度偏差控制在8 K之内。

针对实验和程序计算的平均外壁温度、冷却水平均温度开展误差分析，在不同输入功率和冷却水流速条件下，模拟值与实验值具体如表3所示。

表3 基于不同输入功率与冷却水流速的模拟值与实验值

在输入功率为3 268 W时，误差最大；冷却水流速为0.16 kg/s时，误差率达到3.20%；实验与模拟数值之间的最大均误差为1.62%，严格控制于10%之内，这就表明所构建稳态数学模型的数值模拟结果准确性较高。

不同输入功率条件下，沿管长局部换热系数分布曲线具体如图6所示。

图6 沿管长局部换热系数

由图6可知，在液膜累积越厚的形态下，对应壁面位置的局部换热系数就越小，二者表现为负相关关系；输入功率越大，换热系数越小，二者同样呈现为负相关关系。其中，局部换热系数的最大最小值差异非常大，代表液膜所生成的热阻，可促使热管稳态传热效率下降，以此径向热管启动响应变得越来越慢。

4 结 论

综上所述，本文基于Matlab构建了工业炉径向热管稳态数学模型，且设计了传热计算程序，以输入基础参数，自动计算热管稳定时的局部温度值与最大换热量等相关参数，以此进行了实验与模拟数据对比分析。得出结论：通过实验和程序计算的平均外壁温度、冷却水平均温度开展误差相关分析发现，实验与模拟数值之间的最大均误差为1.62%，严格控制于10%之内，表明所构建稳态数学模型的数值模拟结果准确性较高；基于不同输入功率条件下沿管长局部换热系数分布状态，得知液膜累积越厚，则相应壁面位置局部换热系数越小，二者表现为负相关关系，输入功率越大，换热系数越小，二者同样呈现为负相关关系，局部换热系数的最大最小值差异非常大，代表液膜所生成的热阻，可促使热管稳态传热效率下降，以此径向热管启动响应变得越来越慢。