基于模糊控制理论的机械臂PID控制算法优化设计
2021-10-21郑美茹
郑美茹
(陕西铁路工程职业技术学院 铁道装备制造学院,陕西 渭南 714000)
机械臂可直接替代人工,完成重复机械的生产活动,且在智能化水平不断提高的形势下,对于机械臂控制精确度的要求也随之提高,但受外界环境变化的扰动影响,机械臂控制精确度难以得到保障,使得产品质量也有所下降。所以对机械臂控制进行深入研究具有十分重要的现实意义。姚月琴,王影星,张磊等人,基于抗饱和神经网络动态面控制方法,有效解决了机械臂的外界扰动与输入受限等相关问题[1];梁骅旗,米根锁进行了干扰观测器与滑模控制有机结合的机械臂控制方法设计,切实有效解决了滑模控制抖动与振动等问题[2];许洋洋,王莹,薛东彬等人通过RBF神经网络进行了自适应控制器设计,其中一个作为输入端控制器,另一个作为辨识器,在很大程度上提升了机械臂末端连杆控制稳定性与可靠性[3]。在上述研究基础上,本文基于模糊控制理论进行了机械臂PID控制算法优化设计。
1 基于模糊控制理论的机械臂PID控制算法
1.1 模糊控制
就简单控制系统而言,PID参数调整都是通过工程技术人员既有经验完成的,但是复杂控制系统的参数调整难度较大,动态性能较差,无法确保其平稳性。而PID模糊控制算法属于智能算法,通过模糊控制就机械臂反馈位置、速度信号变化自适应调节PID的相关参数,可有效解决实时变化且复杂的控制问题,以此实现PID调整,并满足系统性能多元化要求。模糊控制结构[4]具体如图1所示。
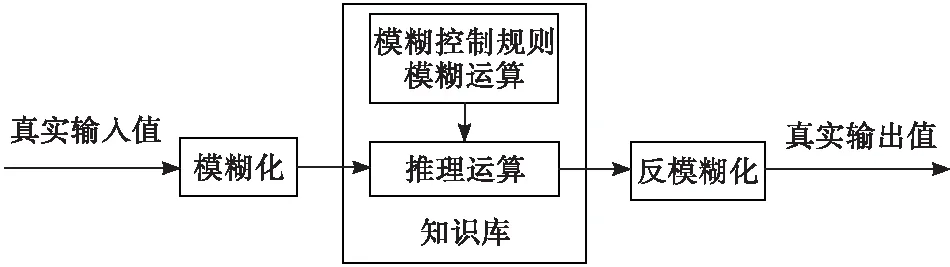
图1 模糊控制结构
其中,模糊化即将实际输入通过模糊集合形式加以表达;知识库即模糊化之后的量需基于知识库进行推理;反模糊化即将模糊推理运算之后的模糊子集清晰明确化之后,输出最终精确值。
1.2 机械臂PID模糊控制
机械臂PID模糊控制原理[5]具体如图2所示。

图2 机械臂PID模糊控制原理
其中,e代表输入误差;ec代表误差变化率。
模糊化机械臂位置输入误差与误差变化率,获得模糊子集(E、EC),根据模糊关系对模糊子集进行逻辑推理,获得输出量(Δkp、Δki、Δkd),反模糊化输出量,转变为精准量(Δkp、Δki、Δkd),将其与常规PID 参数叠加运算,最终获取kp、ki、kd,并传输结果于机械臂,从而实现机械臂控制。
此过程需通过模糊化输入量与输出量、设计模糊控制原则、推理、反模糊化四个环节。
1.2.1 模糊化输入量与输出量
就机械臂而言,模糊控制输入量包含E、EC、Δkd,输出量包括Δkp、Δki。输入量论域设定为[-3,-2,-1,0,1,2,3];输出量论域设定为[-6,-4,-2,0,2,4,6];模糊子集设定为[NB,NM,NS,ZO,PS,PM,PB],分别代表负大、负中、负小、零、正小、正中、正大。通过三角形隶属度函数可获得输入量与输出量隶属度表[6],具体如表1与表2所示。

表1 e、ec、△kd隶属度表

表2 △kp、△ki隶属度表
1.2.2 设计模糊规则
机械臂PID模糊控制规则具体为:误差偏大时,需适度缩小误差,即e过大,则取较大Δkp、Δki与较小Δkd;误差中等时,需适当缩小误差,并避免缩小时出现过度调整,以确保响应速度,即e中等,则缩小Δki;误差偏小时,需有效保障稳定性,避免状态突变,即e过小,则增大Δkp、Δki与缩小Δkd[7]。
1.2.3 模糊推理

(1)
(2)
式中:Dij(E,EC)代表将第一行元素编写为列的形式,第二行到第七行以此类推,紧随第一行。若控制器存在n条模糊规则,那么其模糊关系Q由n条模糊蕴含关系Qij并构而成,具体为
(3)
通过机械臂模糊输入量与输出量的隶属度函数,可得:
(4)
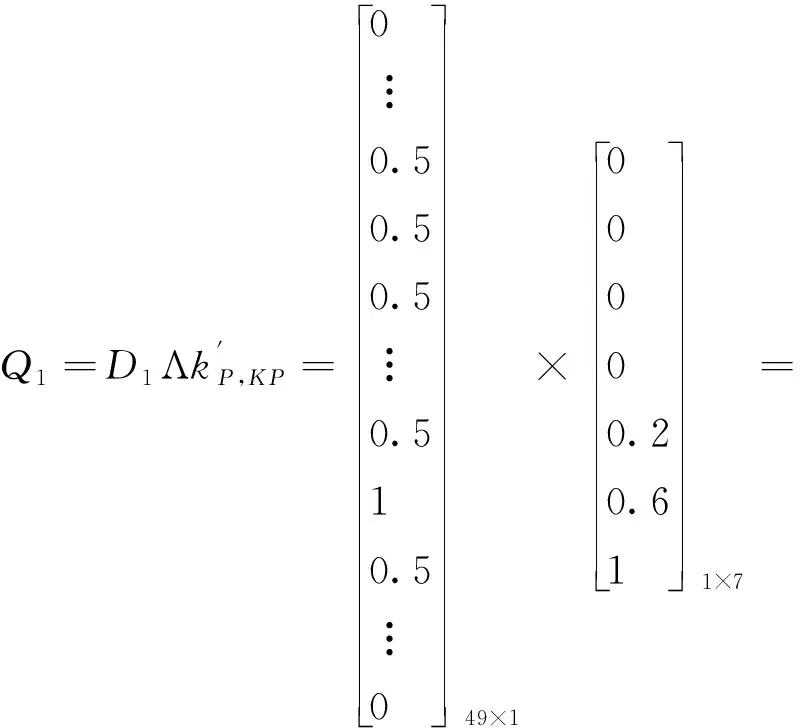
(5)
如此实现了对于Δkp的模糊推理,以此可获得Q2~Q49,同样Δki与Δkd也存在49条规则,推理方法相同。
1.2.4 反模糊化
反模糊化即清晰化模糊推理所得理论,本文选用了最大隶属度的反模糊化方法。就△kp而言,就最大隶属度原则,以隶属度峰值为输出值。针对模糊输出量kp,论域范围为M,精确量为△kp,则:kp=maxfM(Δkp),Δkp⊂M[9]。
反模糊化隶属度查询表格具体如表3与表4所示。
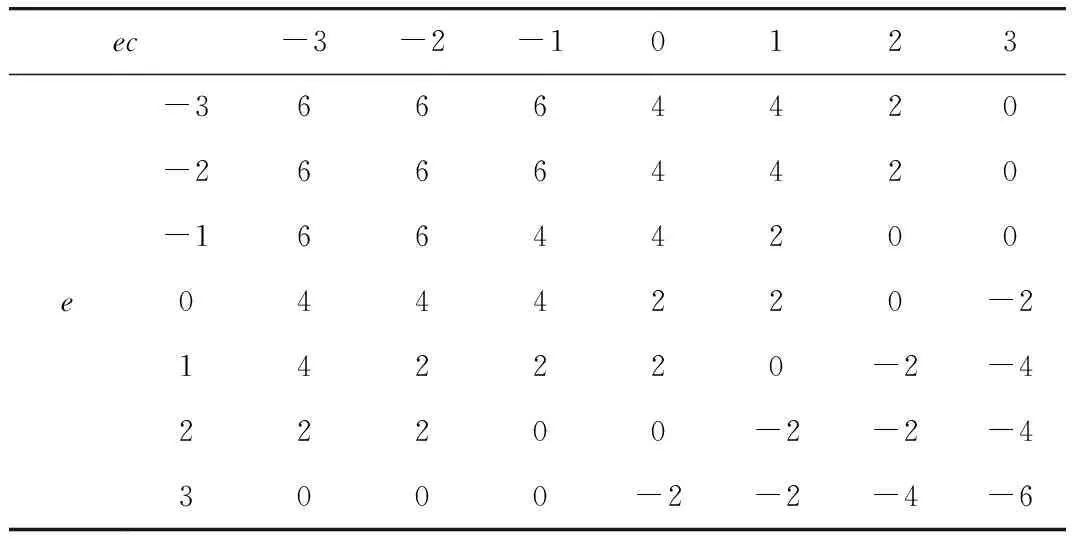
表3 e、ec、△kd隶属度表

表4 △kp、△ki隶属度表
2 仿真分析
2.1 环境设置
以Simulink为仿真环境,对机械臂PID模糊控制算法进行仿真分析。Simulink属于可视化仿真工具,所用Matlab所提供框图工具,不需要编制代码,就可实现动态化建模、仿真。机械臂属于二自由度机械臂结构[10],具体如图3所示。

图3 机械臂示意图
二自由度机械臂参数[11]具体如表5所示。

表5 机械臂参数
由图3和表5可知,二自由度机械臂末端坐标为
简化为
基于Simulink模糊控制器设置仿真参数,合理设置E、EC、Δkp、Δki、Δkd隶属度函数形状,以此为输入量,同时设置相关参数,具体如图4所示。

图4 Simulink参数设置
2.2 结果分析
△kp、△ki、△kd于论域上的输出曲面[9]具体如图5所示。
由图5可知,e、ec分别为PID模糊控制中的输入变量,对应x与y轴;△kp、△ki、△kd分别为PID模糊控制中的输出变量,对应z轴。所以在给定输入变量时,分别存在唯一的输出变量值与其相对应。

图5 △kp、△ki、△kd输出曲面示意图
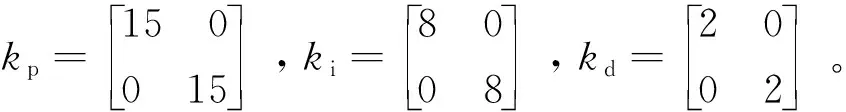
机械臂运动结果具体为:就连杆1而言,在采用机械臂PID模糊控制算法时,响应时间缩短到了0.30 s,达到稳态的时间具体为2.30 s,而通过既有PID控制算法,响应时间为0.54 s,达到稳态的时间具体为5.30 s;就连杆2而言,在采用机械臂PID模糊控制算法时,响应时间缩短到了0.33 s,达到稳态的时间具体为0.95 s,而通过既有PID控制算法,响应时间为0.57 s,达到稳态的时间具体为2.90 s;相对于既有PID算法,机械臂PID模糊控制算法的响应时间与达到稳态的时间都实现了显著优化。
3 结 论
综上所述,本文基于结构复杂的机械臂设计了PID模糊控制算法,其基于既有PID控制算,引进了模糊控制理论,采用了模糊推理方法。并通过Simulink仿真环境实现了仿真分析,给定了Δkp、Δki、Δkd的变化曲面。仿真结果表明,就连杆1而言,在采用机械臂PID模糊控制算法时,响应时间缩短到了0.30 s,达到稳态的时间具体为2.30 s;就连杆2而言,在采用机械臂PID模糊控制算法时,响应时间缩短到了0.33 s,达到稳态的时间具体为0.95 s;相对于既有PID算法,响应时间与达到稳态的时间都实现了显著优化。
