可倾瓦推力轴承的分形表面形貌润滑性能研究

张新宝，范华显

（华中科技大学机械科学与工程学院，湖北 武汉430074）

1 前言

可倾瓦推力轴承是船舶动力装置中重要组成部分，它将螺旋桨产生的推力或拉力传递给船体，推动船舶前进或后退［1］。推力轴承在工作中承受复杂轴向载荷［2］，容易造成轴瓦磨损和轴系振动。轴承表面形貌不仅关系到其摩擦、磨损和润滑，更影响着推力轴承的运行稳定性和振动。

目前，国内外学者对推力轴承的润滑特性做了大量的研究，如瓦块倾斜角、瓦块最小油膜厚度等结构因素对推力滑动轴承性能的影响［3］。轴承润滑性能不仅受到结构等宏观因素影响，也受到润滑表面形貌的微观因素影响。实际上任何表面都是不光滑的，推力轴承润滑表面在微观上都是由许多不规则的凸峰和凹谷组成，这些微观结构在一定程度上影响着轴承的润滑性能和启动运行平稳性［4-5］。由于轴承润滑表面的几何形貌是一个非平稳随机的过程，具有统计相似和自仿射性，即具有分形特征，因此用分形理论来表示润滑表面的形貌结构是有效的［6-8］。

这里基于分形理论的研究，开展关于可倾瓦推力轴承的润滑性能的研究，用分形函数生成润滑表面三维表面形貌，将表面形貌的几何特征参数整合到可倾瓦推力轴承的润滑方程中，用分形法模拟的表面形貌在一定程度上可以反映实际的工程表面，可以通过改变分形函数的相关参数来实现模拟润滑表面几何参数的改变，因此可以实现润滑表面的研究。

2 润滑表面分形几何模型建立

基于分形理论得到模拟表面轮廓的函数模型［9］：

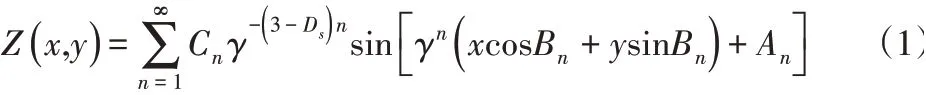
图1 三维随机表面Fig.1 Three-Dimensional Random Surface

3 可倾瓦轴承动压润滑模型

在船舶推进轴系中，可倾瓦推力轴承的轴瓦成均匀对称布置，因此选取其中一片轴瓦进行研究，就可以推测出整个轴承的动载特性，单片轴瓦的结构图，如图2所示。图中：r1-轴瓦内半径；r2-轴瓦外半径；φ-轴瓦圆心角；P-轴瓦支撑筋所在的位置；θp为推力块的支撑线与轴瓦起始边的夹角；hp-推力块在其支撑点处与推力盘的轴向间隙；α-推力盘与推力块间的夹角。

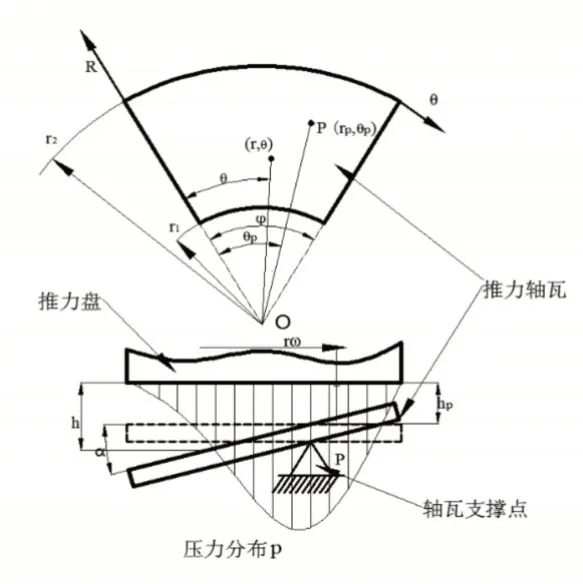
图2 可倾瓦推力轴承油膜厚度图Fig.2 Oil Film Thickness Diagram of Tilting Pad Thrust Bearing

3.1 基本方程

基本上流体润滑理论计算方法是对N-S方程的特殊形式-Reynolds方程的应用和求解［10］。假设轴系在正常工作状态下，油膜是层流的。对于船舶推力轴承来说，为了计算的方便性，建立圆柱坐标系，可得圆柱坐标系下的雷诺方程：

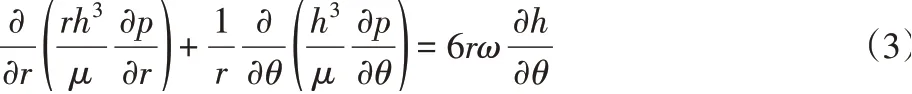
式中：p-油膜压力分布，单位Pa；μ-润滑油动力粘度，单位Pa·s；ω-推力盘的转速，单位rad/s；h-油膜厚度，单位m。式（3）的边界条件为Reynolds边界条件。即润滑油膜边界上的压力为零。

四周边压力边界条件表示为：

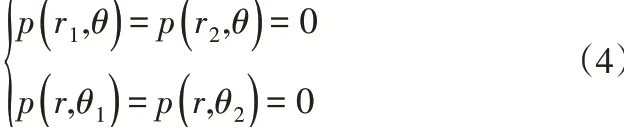
3.2 油膜厚度方程

米切尔式推力轴承在不考虑制造装配误差时油膜厚度包括两部分：支撑点的油膜厚度、绕支撑点倾斜形成的油膜厚度，轴瓦表面处的油膜厚度方程可以表示为下式［11］：

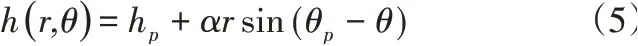
式中：hp-推力瓦支撑中心位置对应的油膜厚度；α-推力瓦绕支撑线OP的倾斜角；θp-推力瓦支撑中心的周向角度；r1＜r＜

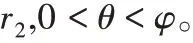
当轴瓦表面和推力盘表面存在形貌误差时，会对油膜厚度产生影响，将推力盘表面形貌和轴瓦表面形貌等效成一个表面的形貌误差，用Δh表示，如图3所示。

图3 有形貌误差的油膜厚度图Fig.3 Oil Film Thickness with Profile Error

则存在形貌误差下的油膜厚度方程为：

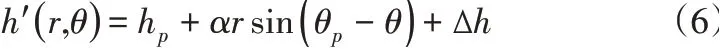
3.3 润滑参数的计算

油膜的承载能力W：

在运动过程中，推力环与油膜之间产生剪应力，产生的油膜摩擦力Ff，在油膜范围内进行积分得到：

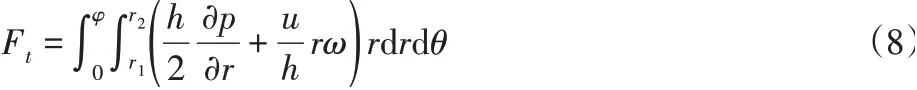
4 模型求解

为了方便方程进行求解计算，定义如下无量量纲：

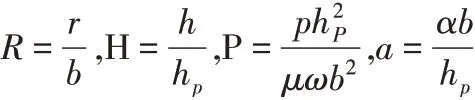
式中：b=r2-r1。对式（3）～（8）进行无量纲化，并采用有限差分法进行求解。

无量纲油膜厚度方程为

对轴瓦表面进行网格划分，将油膜延轴向划分为m格，每个节点用1,2,…,i,…,m+1表示，周向步长Δθ=φ/m，延径向划分为n格，每个节点用1,2,…j…,m+1表示，径向步长为ΔR=1/n，每个单元的节点可以用唯一的形式(i,j)来表示，如图4所示。

图4 润滑油膜有限差分网格Fig.4 Finite Difference Mesh of Lubricating Oil Film

在轴瓦表面上的油膜厚度可以用网格节点上的值来近似表示，因此无量纲化的油膜厚度可以表示为m×n的矩阵：

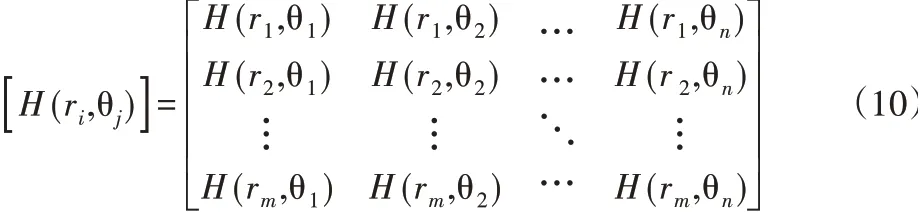
由于表面轮廓的幅值具有随机性，采用公式（2）得到的三维分形表面形貌的幅值轴瓦尺寸位置无关，将式（3）进行无量纲化Z=z/hp，使式（3）和式（9）的维数保持一致，将分形函数得到各节点的幅值整合到油膜厚度中，得到新的油膜厚度：

根据差分原理，任意节点p()i,j的一阶和二阶偏导数都可用周围节点的变量值。故雷诺方程中的一阶偏导数可表示为：

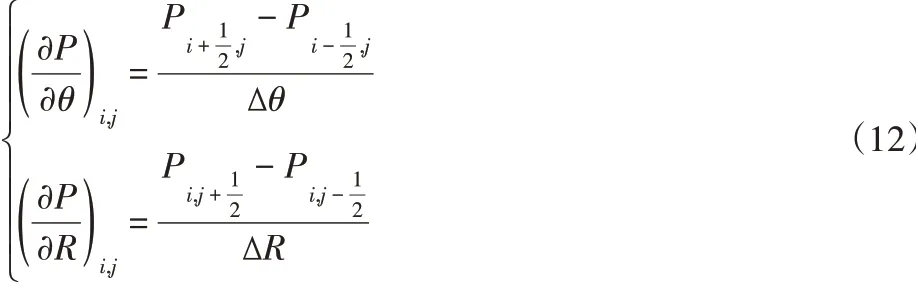
同理二阶偏导数也可以用类似的表示方法。将偏微分方程用差分形式表示后，代入无量纲雷诺方程中去，整理可得：

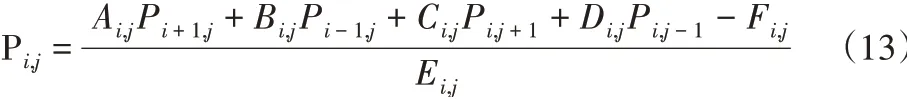
方程中各项系数为：

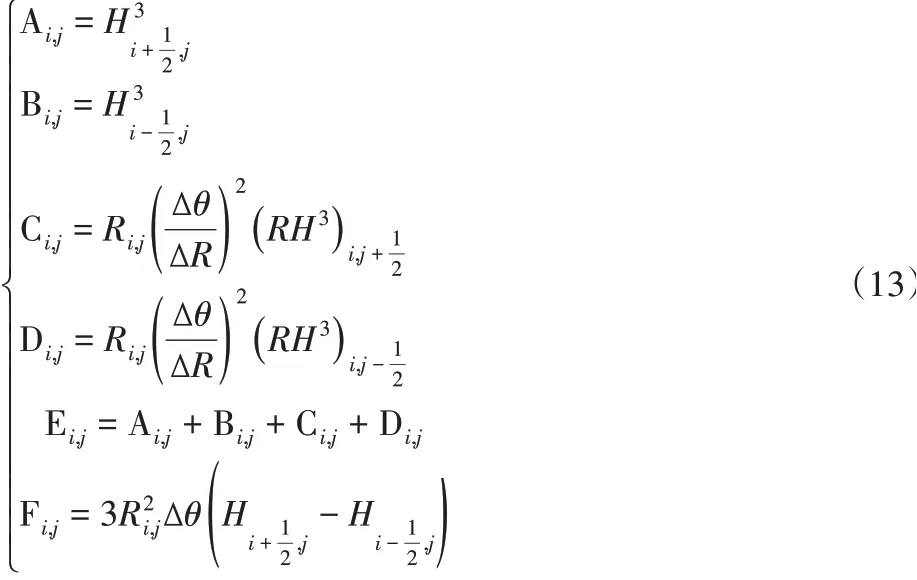
采用松弛迭代法进行求解［12］，通过Matlab软件编程计算，可以得到可倾瓦推力轴承在不同模拟表面形貌下的压力分布p(i,j)，结合式（6）、（7），对可倾瓦轴承推力轴承的求解区域进行积分，可以得到润滑油膜的承载力、摩擦力等润滑参数。计算流程图如图5所示。

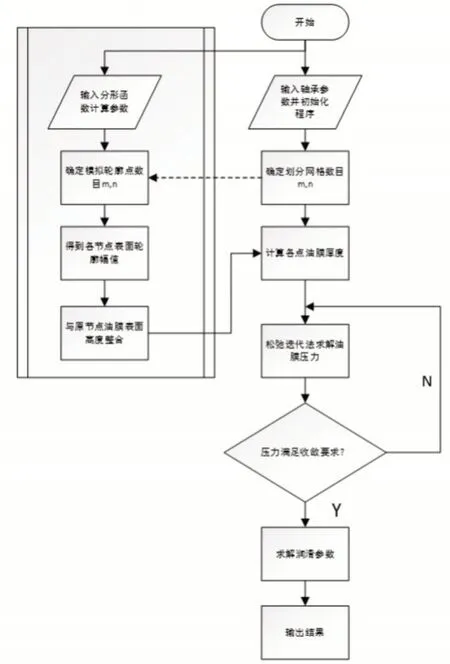
图5 程序求解流程图Fig.5 Flow Chart of Program Solution

5 计算结果及分析

通过改变分形函数中的尺度系数C和分形维数D来表征润滑表面的形貌变化，探究表面形貌的变化对可倾瓦轴承润滑性能的影响。取常数，步距为0.05，共（10×10）个采样点；采用有限差分法计算时，选取网格数m=100,n=100，轴瓦倾角为α=0.003°，轴瓦支撑点油膜厚度hp=10μm，分别改变模拟表面轮廓的D和C值，分析可倾瓦推力轴承的润滑表面幅值及复杂程度对轴承润滑性能的影响。

这里选取某船舶上的可倾瓦推力轴承作为算例分析，该轴承的性能参数如表1所示。首先选取分形维数D=2.5，尺度系数C=1e-4、3e-4、4e-4、5e-4，分析在不同的尺度系数下润滑油膜特性；其次选取尺度系数C=3e-4，分形维数Ds=2.1、2.3、2.5、2.7、2.9，分析分形维数对轴承润滑特性的影响。取推力轴承最大油膜压力及最小油膜厚度所在的位置，分别延轴瓦的径向和圆周方向观察其变化情况。

表1 可倾瓦推力轴承的性能参数Tab.1 Performance Parameters of Tilting Pad Thrust Bearing

如图6可以看出，在特征参数D不变的情况下，油膜厚度变化频率基本相同，随着尺度系数C的逐渐增大，油膜厚度起伏越剧烈，并出现逐渐减小的趋势，同时油膜的最大压力逐渐增大，而且润滑油膜的压力分布波动程度逐渐增大，即整个油膜“震荡”更加剧烈；当尺度系数C为0.0005相比较与尺度系数0.0001，润最小油膜厚度减小了4.5%，油膜最大压力增大10%；当尺度系数变化时单个轴瓦的轴承的整体承载力和摩擦力随着出现波动，但变化程度很小。

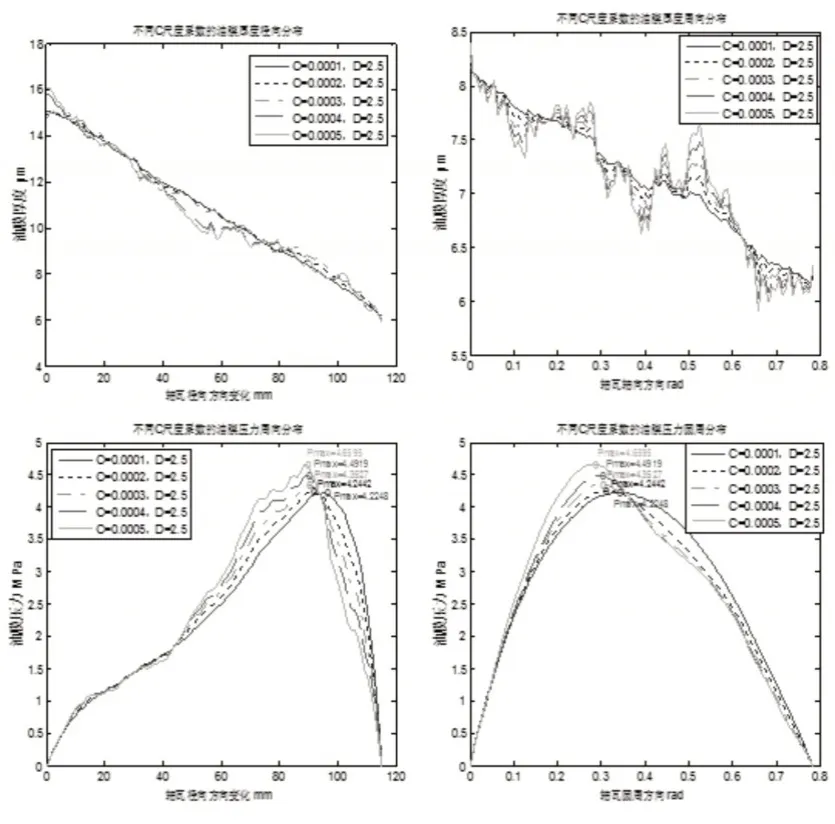
图6 不同尺度系数的影响Fig.6 Effects of Different Scaling Coefficients

如图7所示，在特征参数C不变的情况下，随着分形维数D的逐渐增大，油膜厚度变化频率越来快，对润滑表面形貌的影响也越来越大，使得整个楔形油膜变的更加复杂，油膜厚度变化越来越不稳定，同时最小油膜厚度逐渐减小；分形维数D增大时油膜的最大压力也随着增大，不同分形维数下油膜波动情况不再相同，变的更加复杂，但总体趋势还是在逐渐增大，符合实际表面形貌高度对油膜压力分布的影响规律；当尺度系数D为2.9相比较与分形维数D为2.1，最小油膜厚度减小了约33%，油膜最大压力增大约11.7%；单个轴瓦的轴承的整体承载力和摩擦力也发生变化但变化程度很小。

图7 不同分形维数的影响Fig.7 The Influence of Different Fractal Dimensions

6 结论

（1）这里提出一种考虑表面形貌时可倾瓦推力轴承的数值计算方法，采用分形函数法得到模拟表面形貌幅值，并将整合到可倾瓦推力轴承润滑油膜的数值计算中，从而实现表面形貌变化对润滑特性影响的分析。（2）通过数值计算可以发现，当尺度系数C变大时，楔形油膜厚度最小油膜厚度变小且变化趋势保持一致，油膜的压力分布也随之出现较大的波动；当分形维数D增大时，可倾瓦轴承的油膜厚度曲线和压力分布都变得更加复杂，而且分布趋势不再相同；当两个参数变化时，可倾瓦推力轴承的整体的承载能力和摩擦力出现波动，但变化很小。（3）由上面分析可知，可倾瓦轴系润滑表面形貌误差变化越大，油膜的波动程度变大，不利于整个轴承的承载稳定性，同时也会对推力轴承的刚度造成很大影响，因此在可倾瓦推力轴承的设计制造中要控制润滑表面的加工精度。