巴哈赛车车架多目标拓扑优化设计

鲁春艳，万长东，田 菲

（苏州市职业大学机电工程学院，江苏 苏州215100）

1 引言

拓扑优化是在设计区域内寻找结构的最佳材料分布的优化技术，已成为复杂结构和部件优化的关键技术［1］。巴哈赛车是一种小型越野车，其行驶环境十分恶劣。车架是承载基体，在比赛过程中不仅需要有足够的强度和刚度以承受载荷和冲击，还需要有较高的动态振动频率避免共振，同时轻量化的车架可提高赛车的动力性和经济性。因此在对车架进行拓扑优化时，需要综合考虑多个性能目标。为解决多目标的优化问题需要协调多个目标并进行综合权衡，工程中经常采用折衷规划法，将多个子目标函数加权，归一成一个单目标函数。

在多目标拓扑优化时，子目标权重系数的选择直接影响最终的拓扑结构。目前常用的方法有经验法、层次分析法［2］和正交试验法［3］。经验法是由决策者根据经验赋予权重系数；层次分析法是通过对比子目标之间的重要程度构建决策矩阵，从而求出权重系数。这两者都属于主观赋值范畴，对评价结果的准确性有一定的影响。正交试验法是通过对子目标设置多组权重值，利用正交表进行试验得出最优权重组合，能避免决策者主观因素对权重的影响，但是计算量比较大［4］。

为实现巴哈赛车车架的轻量化设计，选择四种车架的典型工况为刚度优化目标，以及前六阶模态固有频率为动态特性目标，采用折衷规划法，运用灰色关联分析法评价子目标权重系数，建立综合目标函数，对车架进行拓扑优化设计，获得同时满足刚度和振动频率要求的拓扑结构，根据拓扑优化的结果对车架进行二次设计，在保证车架结构性能的条件下，对车架管件截面尺寸进行优化。分析结果表明，改进后的车架强度、刚度和模态固有频率均有提高，轻量化效果明显。

2 多目标拓扑优化数学模型

折衷规划法是将多个子目标函数正规化后加权在一起，形成一个单目标函数。对于静态多刚度目标，可把刚度最大化问题等效为柔度最小化问题来研究。动态振动频率拓扑优化是以提高低阶频率为目标而进行的优化，在优化过程中，将个别阶次的频率作为优化目标并不能代表其他阶次也会正向变化，因此要对各阶次频率进行必要的协调，从而使所有阶次的频率在整体上做到相对最好。因此引入平均频率公式［5］，将平均频率作为优化目标。

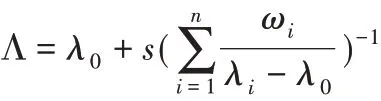
式中：Λ-前n阶的平均频率；λi-第i阶特征频率值；ωi-第i阶频率的加权值；n-频率的阶次；λ0、s-调整目标函数的参数。

基于变密度法材料插值模型，使用折衷规划法结合平均频率法，综合静态多柔度目标和动态振动频率目标的拓扑优化的数学模型如下［6］：

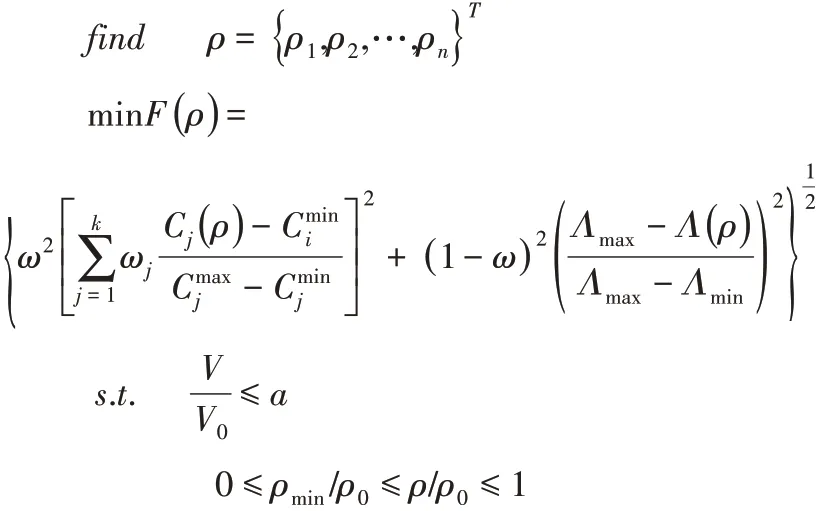
式中：ρ-材料密度；ρmin-材料为空的最小密度值；ρ0-初始单元密度；n-单元总数；F()ρ-综合目标函数；ω-柔度目标函数的权重；k-工况个数；ωj-第j个工况的权重系数，Cj()ρ-工况j的柔度目标函数工况j下柔度目标函数的最大值、最小值；Λ()ρ-平均频率目标函数；Λmax和Λmin-平均频率最大值和最小值；V0和V-优化前、后的体积；a-约束的体积分数，0＜a＜1。

3 灰色关联分析法

灰色关联分析法是分析和确定系统因素间的影响程度的一种方法。系统因素关联度的确定完全依靠客观数据之间的关系，对样本量及样本有无规律没有要求，而且计算量少，不会出现量化结果与定性分析结果不符的情况［7］。采用灰色关联分析法，计算各子目标的关联度，可确定各子目标的权重。灰色关联分析法分析步骤如下［8］：

（1）根据单目标优化结果构建比较序列X。

式中：Xi-第i（i=1，2，...，m）个子目标的优化结果序列；m-子目标总数；n-子目标优化结果总数。

（2）根据各子目标最优值构建参考序列X0。

（3）对比较序列进行无量纲化，无量纲化后形成的序列为X′。

可以采用均值化法进行无量纲化：

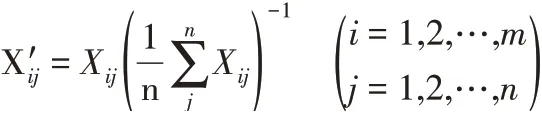
（4）分别计算每个比较序列与参考序列对应元素的关联系数：

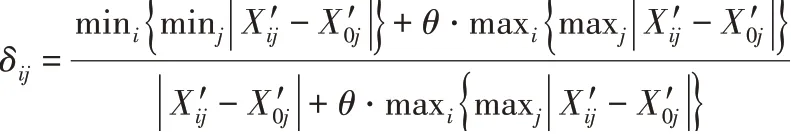
（5）计算比较序列与参考序列的关联度：

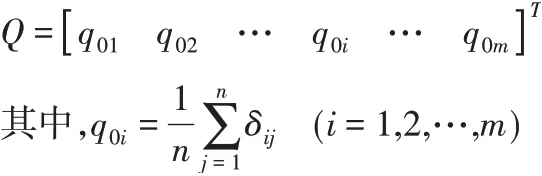
4 车架拓扑优化设计

4.1 车架拓扑优化模型的建立

巴哈车架为金属桁架式，由钢管焊接而成，选用材料为30CrMo，其泊松比为0.279，弹性模量为211GPa，密度为7850kg/m3。根据原始车架，填充设计区域，建立车架拓扑优化有限元模型，如图1所示。深色为不可设计区域，浅色为设计区域，采用壳单元对车架的初始轮廓进行设计。车架前环、车架后部防滚环、防滚环头顶构件以及前端支撑构件是车架的主要构件，防滚环头顶构件之间的横向管件是用来支承车架顶部的，均设置为不可设计区；悬架与车架的连接点采用REB2刚性单元连接，也设置为不可设计区域。

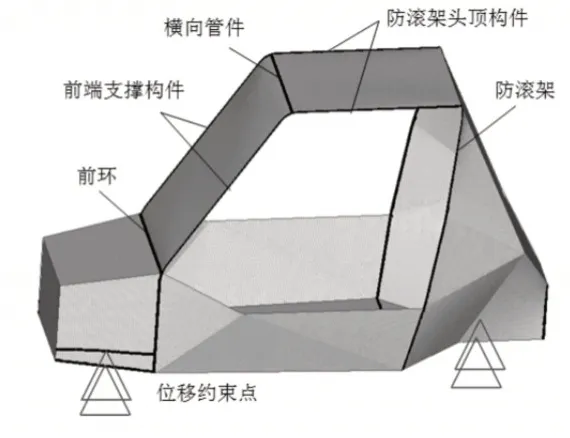
图1 车架拓扑优化有限元模型Fig.1 Frame Topology Optimization Finite Element Model

4.2 静载工况单目标拓扑优化

巴哈赛车需要进行绕桩、跑坡等极限越野项目的比赛，因此选取了弯曲工况和左前轮悬空、右后轮悬空以及左前轮、右后轮同时悬空三种扭转工况进行多柔度拓扑优化［9］。车架承受的载荷及约束方式，如表1所示。

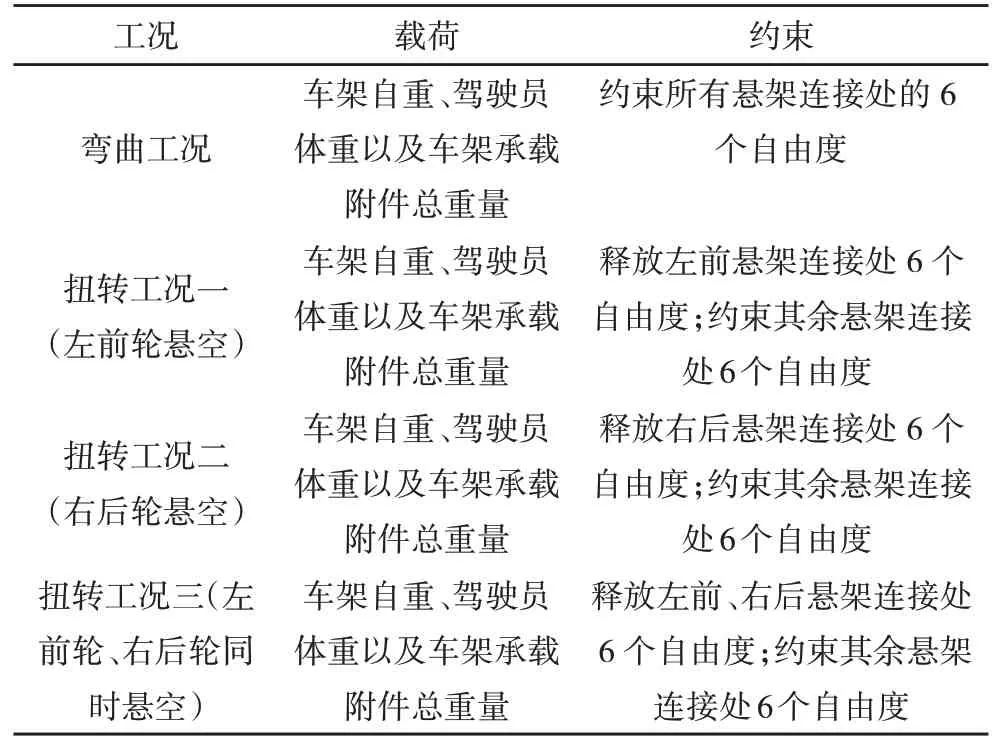
表1 载荷和约束Tab.1 Load and Constraint

以柔度作为优化目标，约束体积分数不大于0.3，对以上四种工况分别进行单目标拓扑优化，各工况拓扑优化结果如图2～5。从out文件中可查看各工况优化前后的最大最小柔度值

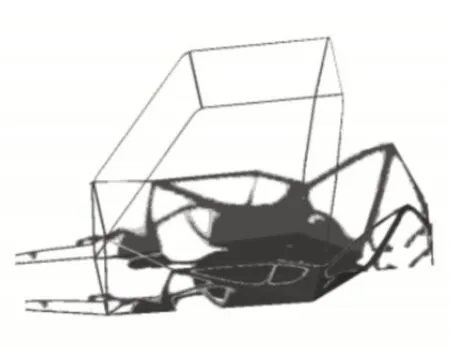
图2 弯曲工况Fig.2 Bending Condition

从图2弯曲工况拓扑结构可知，材料主要分布在座舱底部及两侧，前后舱均没有出现较完整材料分布，这是因为座舱承受了大部分的整车载荷。如图3～5所示，座舱底部均没有材料分布。如图3所示，出现了较清晰的车架前部抗扭桁架结构。如图4所示，出现了较清晰的车架后部抗扭桁架结构。如图5所示，出现了较清晰的车架中部抗扭桁架结构。拓扑结果与边界条件的施加相一致。

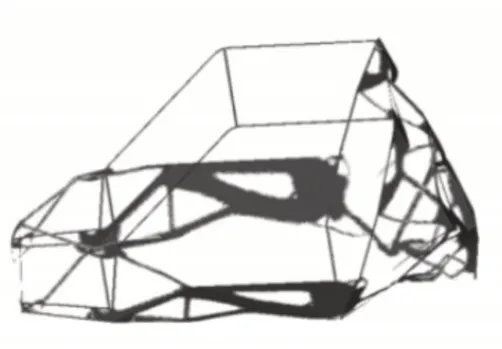
图3 左前轮悬空Fig.3 Left Front Wheel Dangling

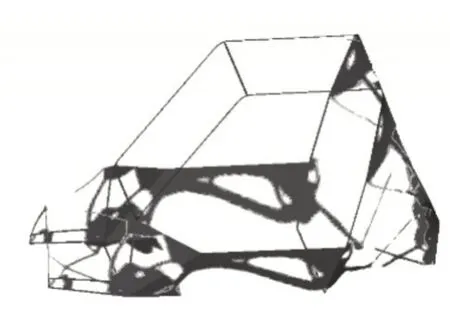
图4 右后轮悬空Fig.4 Right Rear Wheel Dangling Right Rear

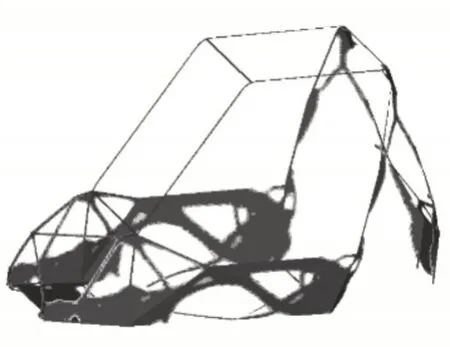
图5 左前、右后轮同时悬空Fig.5 Left Front and Wheels Dangling

4.3 动态固有频率拓扑优化

动态拓扑优化的主要目标是为了提高车架的低阶固有频率。定义一个加权特征频率响应，设定前6阶频率的权重值均为1/6，使用该响应可以增加低阶模态频率的提高对目标函数所产生的影响。以前6阶平均频率最大为优化目标，约束体积分数，提交计算，得到结果如图6所示。从out文件中可获得Λmax和Λmin的值。

从图6的优化结果可以看出，在车架中部优化出了比较清晰车架上、下边梁结构，在车架的前环、防滚架与下车架边梁之间出现了一些小尺寸的孔洞，其作用类似于为提高固有频率所增加的加强筋。

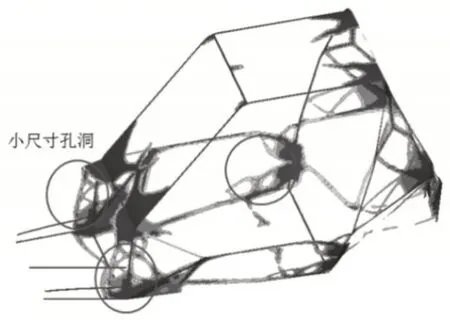
图6 车架固有频率拓扑优化结果Fig.6 Results of Frame Natural Frequency Topology Optimization

4.4 车架多目标拓扑优化

进行多目标拓扑优化时，采用灰色关联分析法来确定各子目标的权重系数。将各子目标优化后的结果形成的序列作为比较序列，每一行表示单目标优化时各子目标对应的性能值，各子目标最优值形成的序列作为参考序列。由于柔度和频率量纲不同，不便于比较，采用均值化法对参考序列的数据无量纲化处理。调节系数θ取0.5，计算出各个子目标的综合关联度，如表2所示。

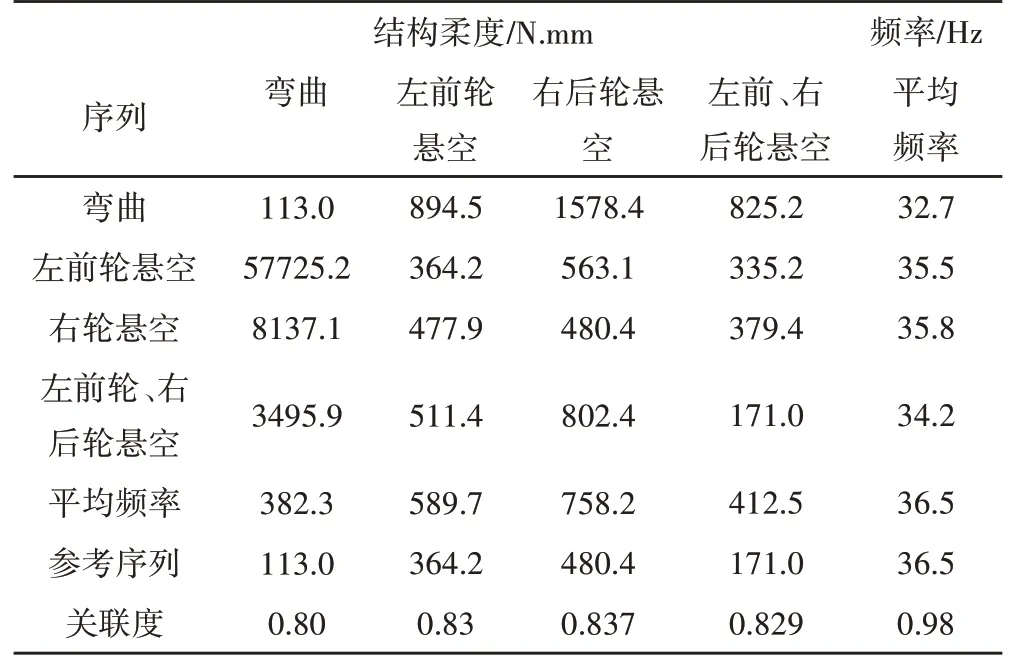
表2 灰色关联序列Tab.2 Grey Relational Sequence

根据关联度计算各子目标的权重系数分别为0.187，0.194，0.196，0.194，0.229。

将各项数据带入综合目标函数F（ρ）中，约束体积分数，经过55步迭代，综合目标函数逐渐减少并最终达到稳定值，如图7所示。

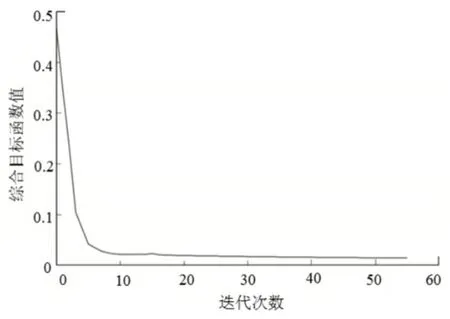
图7 综合目标函数迭代历程Fig.7 Comprehensive Objective Function Iteration Process

从图8可以看出，各目标函数对应的工况都有相同的波动趋势；随着迭代过程的进行，各个工况的柔度值平稳降低。

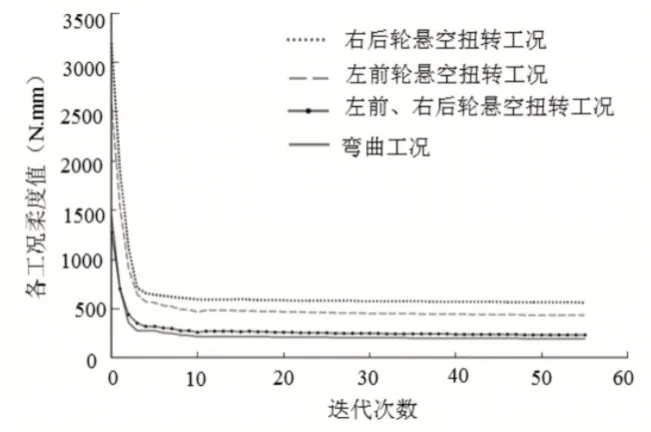
图8 各工况柔度迭代历程Fig.8 Iteration Course of Flexibility In Various Operating Conditions

由图9可以看出，前六阶固有频率逐渐增加，且各阶频率之间无交叠现象，证明以平均频率作为优化目标是可行的。由图8、9可知结构的刚度和频率都有所提高。

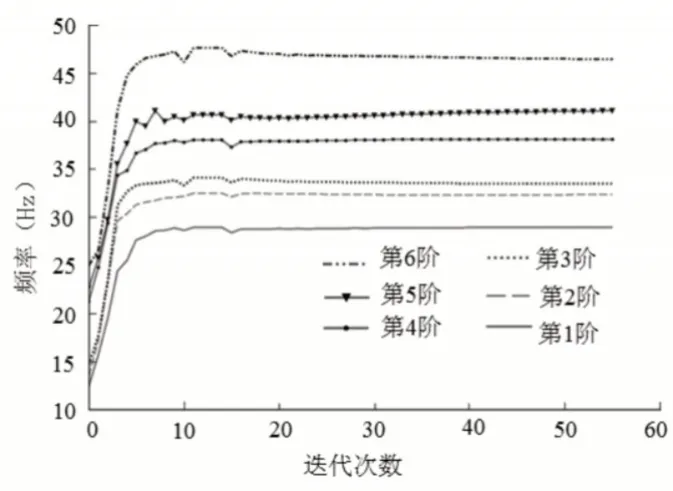
图9 各阶频率迭代历程Fig.9 Iteration Process of Each Order Frequency

从图10可以看出，车架前部、中部、后部都拓扑出来比较清晰的材料分布路径，车架的轮廓基本形成。

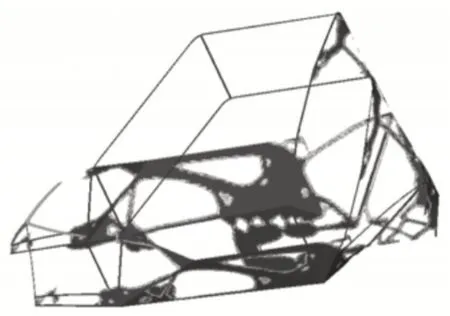
图10 车架拓扑优化结果图Fig.10 Results of Frame Topology Optimization

4.5 提取拓扑结果与车架建模

根据拓扑结果对车架进行二次设计，对于单元密度大的区域采用管径大、壁厚的钢管，对于单元密度小的区域采用管径小、壁薄的钢管。原始车架采用了3种不同型号的钢管，因此新设计的车架钢管型号沿用原始车架，如图11所示，主要结构件（深色）采用1号钢管，钢管外径为31.75mm，壁厚1.8mm；次主要结构件（次浅色）采用2号钢管，其外径为25.4mm，壁厚1.6mm；次要结构件（最浅色）采用3号钢管，其外径为25.4mm，壁厚1.3mm。

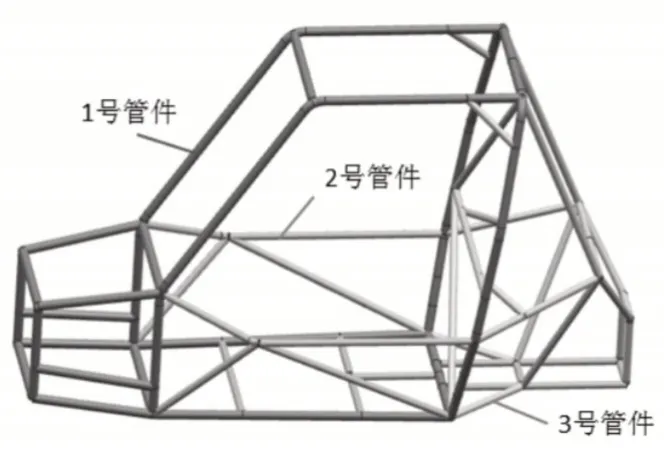
图11 拓扑优化后设计的车架三维模型Fig.11 Three-Dimensional Model of Vehicle Frame Designed After Topology Optimization

5 车架轻量化设计

5.1 尺寸优化

对二次设计的车架进行强度分析，发现存在较大的应力富余，在保证车架性能的同时，对车架钢管进行尺寸优化。设定管件的外径不变，选取三种类型的钢管内径作为优化的设计变量（外径尺寸不变，改变内径即改变厚度），采用响应面法对车架质量进行优化［10］。设定设计变量的优化尺寸范围为原尺寸的（90～110）%。设置目标函数：车架质量最小，车架扭转变形最小，最大弯扭应力在一定范围内最小，车架一阶固有频率在一定范围内最大。计算得到的优化数据如表3所示。

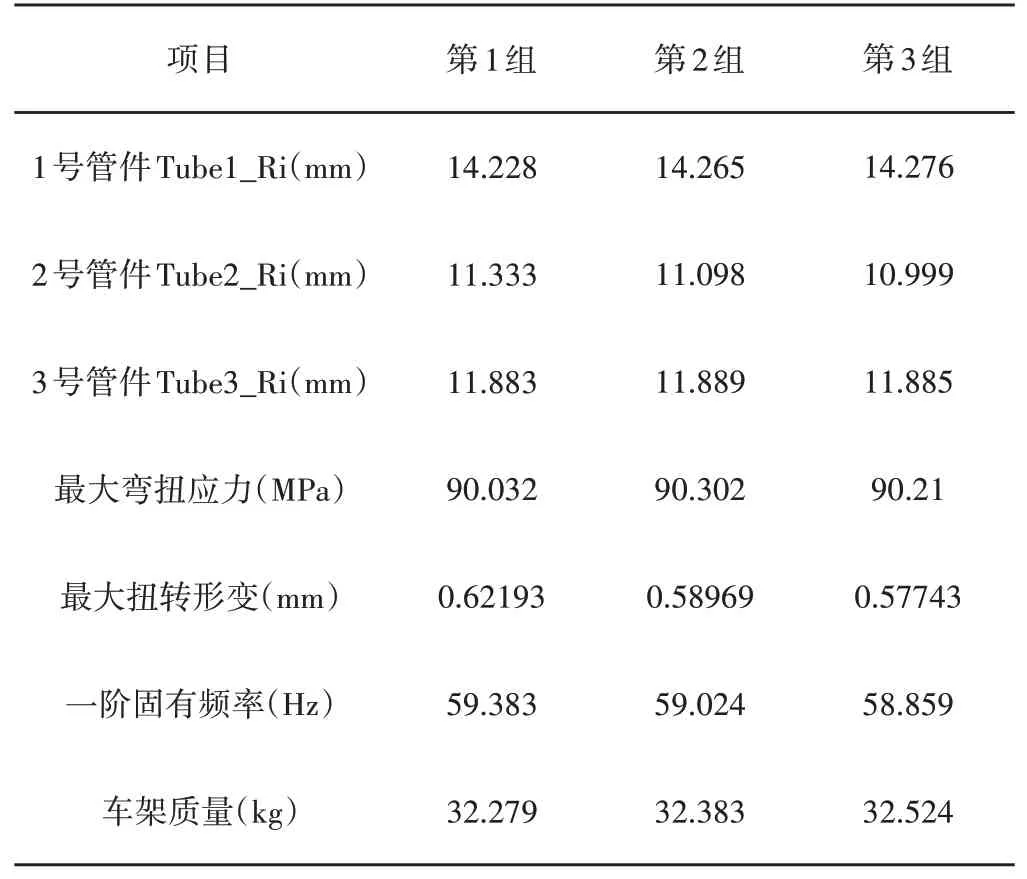
表3 尺寸优化结果Tab.3 Size Optimization Results

从表3的结果来看，第一组数据为最优，得到的车架质量最小，考虑到实际的钢管型号，对优化结果进行了调整，最终采用的管件厚度，如表4所示。

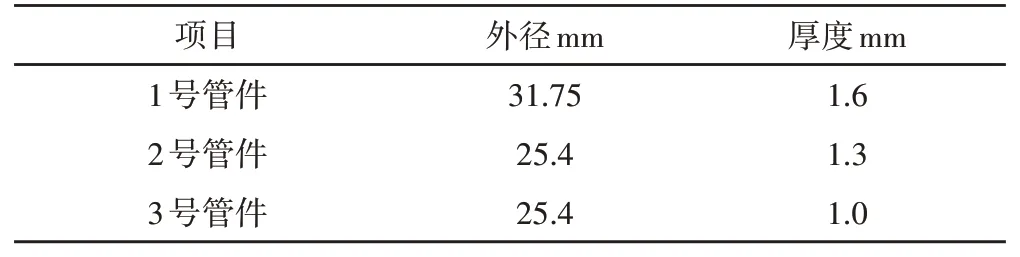
表4 优化后管件尺寸Tab.4 Optimized Pipe Fitting Size

5.2 车架结构性能分析验证

根据调整后的管件尺寸，修改车架三维模型，重新建立了车架的有限元模型，对尺寸改进后的车架进行强度、刚度、模态分析。车架优化前后的仿真结果，如表5所示。

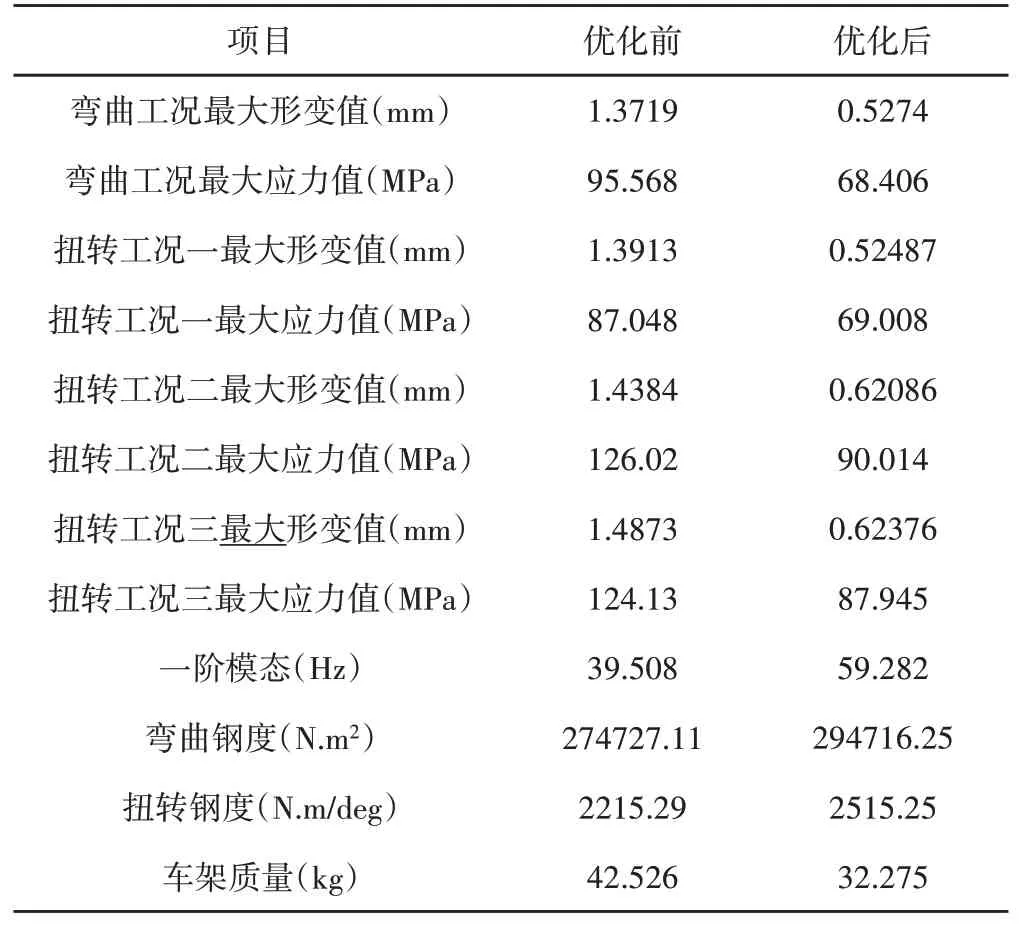
表5 车架优化前后结构性能对比Tab.5 Structural Performance Comparison Before and After Frame Optimization

经过拓扑优化和尺寸优化后的车架在各工况下的应力均小于原始车架，且远小于材料的屈服强度；各工况的形变也小于优化前；一阶固有频率为59.28 Hz，比原始车架的39.25 Hz大幅度增加；车架的质量由原来的42.526kg减少至32.275kg，减轻了24.1%。在车架轻量化的同时改善了车架的结构性能，表明拓扑优化是成功的。

6 结论

（1）将折衷规划法引入到巴哈车架的多目标拓扑优化设计中，建立了综合刚度和频率的多目标拓扑优化数学模型，实现了车架的多目标拓扑优化。

（2）采用灰色关联分析法确定子目标的权重系数，避免了主观因素对于权重的影响，使子目标的权重系数分配更加合理，为处理多目标优化问题提供了参考。

（3）根据拓扑优化的结果对车架进行二次设计，并对车架管件的截面尺寸进行优化，通过对优化前后车架结构性能分析可知，优化后的车架刚度、强度、固有频率均有提高，车架质量减轻24.1%，证明了优化的可行性。