断屑钻尖后刀面的砂轮磨削位姿算法

马玉豪 李 勇 江 磊 丁国富

西南交通大学机械工程学院，成都，610031

0 引言

钻尖作为钻头的重要结构，具有定心、控制切屑长度与毛刺状况的作用，并且会影响钻头的强度。针对不同钻削工况，钻尖存在多种结构形式。断屑钻尖是一种新型的钻头端齿结构，具有较高的孔底切削和断屑能力。断屑钻尖结构具有三段切削刃，中心钻尖直线刃、外侧钻尖直线刃使得切屑受力方向不同而提高断屑性能，中间的钻尖圆弧刃能改善钻尖的受力情况，可减小应力集中和延长使用寿命。对应于切削刃的分段，断屑钻尖也存在两个钻尖角——较小的中心钻尖角能提高钻头定心性能，较大的外侧钻尖角能减小孔的边缘变形并改善毛刺状况。断屑钻尖的各钻尖角以及切削刃的长度，需要根据对应的加工材料、孔直径和工艺参数确定。

断屑钻尖后刀面是断屑钻尖结构的关键几何特征，也是断屑钻尖制造工艺的难点和重点。目前，针对刀具后刀面的磨削加工，许多学者已经进行了相关研究工作。梁志强等[1]研究了等径向后角微细球头铣刀刃磨工艺；张潇然[2]研究了圆弧头立铣刀端齿部分的刀刃曲线数学模型和磨削工艺算法模型；HAN等[3]推导出了圆弧头立铣刀具有齿偏和齿过刃线的数学模型以及端齿前后刀面砂轮磨削轨迹；孙晓军等[4]对球头立铣刀进行了数学建模，将各个加工部位参数化，提出了高精度后刀面加工算法；刘长玲[5]研究了球头立铣刀的前刀面、两个后刀面以及螺旋槽的加工方法；CHENG等[6]构建了具有齿偏心中心的球头S形刃线数学模型，并通过仿真软件与实际机床进行了验证；宾鸿赞等[7]提出了一种采用CBN球面砂轮数控磨削复杂形状刀具的新磨削加工工艺，实现了球头铣刀不同形状刀体接合处前刀面的光滑过渡；周焱强等[8]建立了钻头圆锥面后刀面的数学模型；房晨等[9]利用三维软件建立了钻头模型，并利用锥面刃磨法对钻头后刀面磨削轨迹进行了研究；易格等[10]建立了钻削功率与钻头后刀面几何参数之间的关系模型。目前，人们对常规钻尖及立铣刀端齿前后刀面磨削工艺的研究已较为成熟，然而针对断屑钻尖后刀面的磨削工艺研究还不完善，且相关文献报道较少。

本文针对断屑钻尖后刀面砂轮磨削位姿进行数学建模，根据工程应用要求和砂轮运动约束条件，借助于运动学理论和坐标变换矩阵，给出了断屑钻尖后刀面的砂轮磨削位姿算法，提高了断屑钻头的断屑性能与制造精度。

1 断屑钻尖后刀面的结构参数定义

为了完整准确地描述断屑钻尖后刀面结构，定义以下结构参数：①中心钻尖角χ(即中心钻尖直线刃线绕钻头轴线回转所形成的锥角)；②外侧钻尖角θ(即外侧钻尖直线刃线绕钻头轴线回转所形成的锥角)；③中心钻尖直径D(即两直线刃线理论交点绕钻头轴线回转所形成的圆轮廓直径；④外侧钻尖直径D1(即外侧钻尖直线刃线与周齿螺旋刃的交点绕钻头轴线回转所形成的圆轮廓直径；⑤钻头周刃长度Lw(即周齿沿钻头轴线方向的长度)；⑥钻尖圆弧半径r(即钻尖圆弧刃线的圆弧半径)；⑦锥度角κ(即周齿回转轮廓母线与钻头轴线的夹角)；⑧周刃螺旋角β(即周齿回转轮廓母线与周齿刃线切矢的夹角)；⑨后角λ(即后刀面在刃线法截面的轮廓与钻头轴线法截面的夹角)；⑩后刀面宽度W(即后刀面在刃线法截面的轮廓长度)。其中参数①～⑧如图1所示，参数⑨、⑩如图2所示。

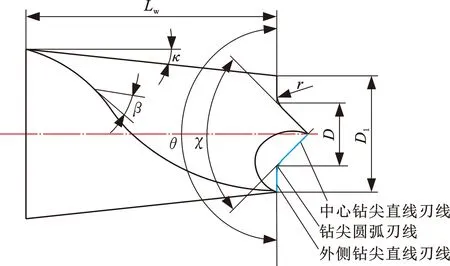
图1 断屑钻尖后刀面结构示意图Fig.1 Structural diagram of flank face of cutting-breaking drill tip

图2 后刀面剖面及坐标系Fig.2 Profile of flank face and coordinate systems

由以上部分结构参数可推导出周齿回转角φ(即周齿螺旋刃从尾部起点至断屑钻尖后刀面终点的绕钻头轴线回转角度)，如图2所示。周齿回转角的计算表达式为

(1)

2 坐标系定义及变换

2.1 坐标系定义

为了便于断屑钻尖三段刃线的参数化建模以及砂轮磨削位置和姿态的描述，建立图2所示的三个坐标系。

(1)工件坐标系OWXWYWZW：原点OW位于钻头尾端圆心，坐标轴ZW为钻头轴线，坐标轴XW由原点OW指向周齿刃线起点。为了便于工具磨床后置处理，砂轮磨削轨迹的刀位坐标都需要在工件坐标系下进行描述。

(2)钻尖坐标系OTXTYTZT：原点OT位于两直线刃的理论交点，坐标轴ZT平行于坐标轴ZT，坐标轴XT垂直于第一后刀面刃线与钻头轴线所在的平面。刃线数学模型的建立以及砂轮磨削姿态的完整定义均基于钻尖坐标系。

(3)刃线法截面坐标系ONXNYNZN：原点ON位于第一后刀面刃线上，坐标轴XN与坐标轴XT平行，坐标轴YN为原点ON处的刃线切线。该坐标系为浮动坐标系，用以约束砂轮的磨削姿态。

2.2 坐标系变换矩阵构建

为了便于采用运动学理论进行砂轮磨削位姿的求解，本文构建了如下齐次坐标变换矩阵。

(1)由刃线法截面坐标系到钻尖坐标系的变换矩阵MN→T。该变换矩阵的描述为，刃线法截面坐标系先绕XN轴旋转至与钻尖坐标系平行，再平移至与钻尖坐标系重合。定义第一后刀面刃线上任意点P1的坐标在钻尖坐标系下的表达为P1_T，即

(2)

则变换矩阵MN→T可表示为

(3)

其中，Ag为点P1的刃线切矢与坐标轴YT的夹角。当点P1位于不同刃线段时，夹角Ag的计算方式不同：

当点P1位于外侧钻尖直线刃线段时，有

(4)

当点P1位于钻尖圆弧刃线段时，有

(5)

当点P1位于中心钻尖直线刃线段时，有

(6)

(2)由钻尖坐标系变换到工件坐标系的变换矩阵MT→W。该变换矩阵的描述为，钻尖坐标系先绕坐标轴ZT旋转回转角φ与工件坐标系平行，再平移至与工件坐标系重合。则变换矩阵MT→W可表示为

(7)

3 断屑钻尖刃线的数学建模

由钻尖坐标系的定义可知断屑钻尖刃线位于坐标平面OTYTZT内，则断屑钻尖刃线可分段表达为如下三个数学模型。

(1)外侧钻尖直线刃线的数学模型。在钻尖坐标系下，外侧钻尖直线刃线上任意点P1的坐标可表达为

(8)

(2)钻尖圆弧刃线的数学模型。在钻尖坐标系下，钻尖圆弧刃线上任意点P1的坐标可表达为

(9)

y2≤yP1_T≤y1

(3)中心钻尖直线刃线的数学模型。在钻尖坐标系下，中心钻尖直线刃线上任意点P1的坐标可表达为

(10)

为了减少后刀面摩擦，断屑钻尖可能存在多个后刀面。在钻尖坐标系下，本文通过对上述后刀面钻尖刃线模型进行扩展，以满足第二、三后刀面的几何定义。如图2所示，第二后刀面刃线只需根据第一后角和第一后刀面宽度在钻尖坐标系下将第一后刀面刃线进行偏移即可，则第二后刀面刃线上任意点P2的坐标在钻尖坐标系下可表达为

(11)

以此类推，可得到第三后刀面刃线上任意点的坐标表达式。

4 砂轮磨削轨迹的位姿计算

4.1 砂轮磨削姿态定义

刀具后刀面的磨削工艺通常采用11V9碗形砂轮，本文以砂轮轴矢量Fg(即碗形砂轮大端圆心指向小端圆心的方向矢量)描述砂轮的磨削姿态。为了保证磨削过程中砂轮姿态的一致性，如图3所示，在钻尖坐标系下定义砂轮初始磨削姿态，包含如下两个约束条件：①砂轮大端圆切矢F1与后刀面在刃线法截面的轮廓重合；②砂轮轴矢量Fg与刃线上点P1处的后刀面垂直。

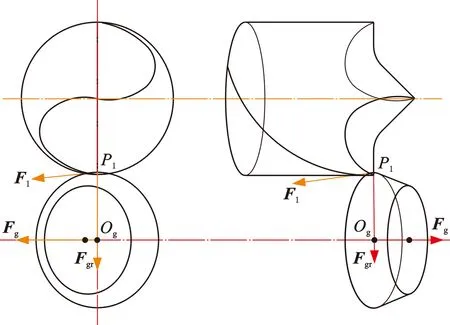
图3 砂轮初始磨削姿态Fig.3 Initial grinding pose of grinding wheel

由上述定义，切矢F1在刃线法截面坐标系下可表达为

(12)

在钻尖坐标系下可表达为

F1_T=MN→TF1_N

(13)

砂轮轴矢量Fg在钻尖坐标系下可表达为

Fg_T=F1_T×FY_T

(14)

其中，FY_T为坐标轴YT的单位矢量。

定义刃线上点P1指向砂轮圆心Og的径向矢量为Fgr，它在钻尖坐标系下可表达为

Fgr_T=Fg_T×F1_T

(15)

为了避免实际磨削过程的干涉问题，在砂轮初始磨削姿态的约束下，本文引入磨削抬角δg。定义抬角δg为砂轮绕矢量F1旋转的角度，在保证后刀面磨削精度的基础上，使砂轮的磨削姿态具有一定的调整空间，如图4所示。

图4 增加抬角后的砂轮磨削姿态Fig.4 Grinding pose of grinding wheel with lifting angle

定义绕空间任一单位矢量N(Nx，Ng，Nz)旋转角度α的变换矩阵为

(16)

F′g_T=Rot(F1_T，δg)Fg_T

(17)

F′gr_T=Rot(F1_T，δg)Fgr_T

(18)

4.2 砂轮磨削轨迹计算

以砂轮大端面圆心点Og的坐标描述砂轮磨削位置，其约束条件为磨削过程中砂轮的大端圆始终与刃线接触。以第一后刀面磨削为例，圆心点Og在钻尖坐标系下可表达为

(19)

其中，Rg为砂轮大端面圆周半径。

4.3 砂轮磨削刀位点计算

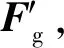
Og_W=MT→WOg_T

(20)

(21)

5 加工验证

表1 断屑钻尖后刀面的结构设计参数Tab.1 Structural design parameters of flank face of cutting-breaking drill tip

表2 断屑钻尖后刀面的磨削工艺参数Tab.2 Grinding processing parameters of flank face of cutting-breaking drill tip

实际磨削的断屑钻尖后刀面如图5所示。为进一步验证所提算法的计算准确性，利用某PG1000刀具检测仪对实物的结构进行了测量，检测数据如表3所示。

图5 断屑钻尖后刀面的实际磨削结果Fig.5 Actual grinding result of flank face of cutting-breaking drill tip

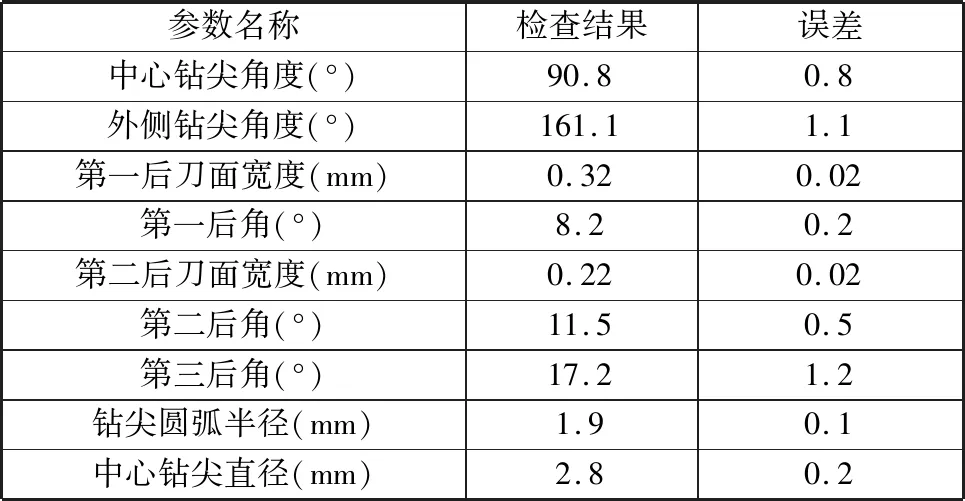
表3 断屑钻尖后刀面的实际测量结果Tab.3 Actual measurement result of flank face of cutting-breaking drill tip

测量结果表明，所提出的砂轮磨削位姿算法可基本满足断屑钻尖后刀面的设计和加工要求，但由于砂轮微量磨损导致磨削点发生偏移，使得实际后角和后刀面宽度还存在微小误差，可以通过相应的补偿方式来进一步提高加工精度。

6 结语

对断屑钻尖后刀面的结构参数以及相关坐标系进行了定义，建立了钻尖后刀面刃线的数学模型；应用运动学原理并基于磨削工艺的约束条件，推导出了基于工件坐标系的砂轮磨削位置和姿态求解的数学模型；通过实际加工和测量，验证了所提砂轮磨削位姿算法的有效性。所提算法可应用于断屑钻尖多重后刀面加工，并可灵活调整砂轮磨削姿态。