基于坡体含水率分布的非饱和土边坡上限分析方法
2021-10-20孙志彬杨胜宇聂秀鹏侯超群谭晓慧
孙志彬, 王 振, 杨胜宇, 聂秀鹏, 侯超群, 谭晓慧
(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009;2.合肥工业大学 资源与环境工程学院,安徽 合肥 230009)
引言
大部分人工或自然边坡为非饱和土边坡,土体强度受基质吸力影响较为明显。受地下水位高度等因素影响,非饱和边坡的基质吸力分布存在明显的非均匀特征,进而导致边坡的土体强度也表现非均匀特性。因此,考虑基质吸力影响的非饱和土边坡稳定分析问题,是道(铁)路工程中研究热点和难点之一。
国内外学者采用数值模拟或理论分析方法对非饱和土边坡稳定性展开研究。数值模拟主要基于有限元或者有限差分手段开展,文献[1]利用Seep/W有限元软件对非饱和土坡进行建模分析,重点考察了基质吸力变化对边坡稳定性的影响;在已知黄土基质吸力和抗剪强度相关特性的基础上,文献[2]运用GeoStudio有限元软件分析了不同降雨强度、降雨时长对坡稳定性的影响。
考虑到数值模拟建模流程复杂且需要较长的运算时间,有学者采用理论方法对非饱和土边坡稳定性开展了研究。文献[3]采用简化的Bishop抗剪强度公式建立了非饱和土边坡的稳定方程,研究结果指出基质吸力的存在对边坡稳定性有较大影响;文献[4]基于极限分析方法研究了非饱和土边坡的三维稳定性,并讨论了基质吸力均匀、线性分布下的稳定性指标的变化情况;文献[5]通过现场试验获取边坡含水率、基质吸力随深度变化关系,并采用无限边坡法分析了不同季节土体基质吸力变化对边坡稳定性的影响。
上述工作为研究基质吸力变化对非饱和土边坡稳定性的影响提供了重要参考。在确定边坡基质吸力分布时,目前研究一般采用试验实测数据或进行简化假设的方式进行,但均存在一定缺点。开展基质吸力的实际量测能够获取工程边坡的基质吸力分布,但所需量测成本较大,获得结果的普适性有待进一步考量。对基质吸力分布进行简化假设建模有利于工程上的广泛应用,但基质吸力的分布形式大多呈现非线性,如何建立合理的分布模型需要进一步研究。与基质吸力相比,非饱和土边坡土体含水率的现场量测与计算分析相对简单。在获取土水特征曲线的基础上,通过土体含水率来确定边坡基质吸力的大小,进而分析非饱和土边坡的稳定性,可以在避免对基质吸力开展现场量测情况下,获取较为可靠的基质吸力分布规律。
本文基于极限分析上限定理,利用边坡含水率分布方程与非饱和土水特征模型,拟合了非饱和土边坡基质吸力沿坡高分布的曲线。在此基础上采用边坡上限分析模型与能量耗散平衡方程,建立基于含水率特征参数的非饱和土边坡的安全系数计算方法。初步讨论了土体强度、吸力摩擦角、边坡几何形状等因素对边坡稳定性的影响,为考虑基质吸力的非饱和土边坡的稳定性分析提供了一种新的计算方法。
1 理论与方法
1.1 非饱和土强度及边坡基质吸力分布
非饱和土体抗剪强度受基质吸力影响,为描述非饱和土抗剪强度,学者们提出了一系列非饱和土强度公式,其中以Fredlund提出线性强度公式较有代表性。该公式将正应力和基质吸力作为控制土体抗剪强度的双应力状态变量,描述了基质吸力对土体抗剪强度的贡献[6-7],表达式为:
τf=c′+(σ-μa)tanφ′+(μa-μw)tanφb
(1)
由(1)式可知,了解边坡各点基质吸力大小,获取基质吸力的空间分布,是正确求解非饱和土边坡的剪切强度场,并进行可靠的稳定性分析的关键。
边坡基质吸力的分布形式与地下水位密切相关,如图1所示。当地下水位较深时,边坡基质吸力沿深度呈均匀分布,大致符合曲线①所示。对于地下水位附近的土体,基质吸力随高度线性增大,大致符合曲线②所示。曲线③及④表示边坡地下水位以上较大范围内土体的基质吸力情况。
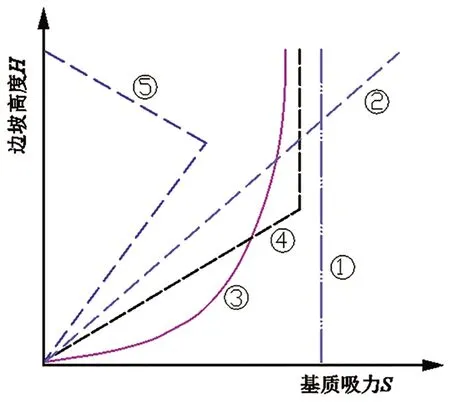
图1 非饱和边坡中几种假设的基质吸力分布[9]Fig.1 Matric suction distribution of several hypotheses in unsaturated slope
曲线①、②中的吸力模型较易求得,学者们据此建立了基质吸力的均匀分布以及线性分布假设[10],并将其应用于非饱和土边坡的稳定性分析中。但由于①、②情况仅限于地下水位较深或较浅的情况,对于一般地下水位情况,①、②假设与实际的基质吸力分布之间存在较大的差异。当应用于大型的实践工程当中时,不可避免地会造成计算结果与实际情况之间的误差。
如何获取基质吸力,尤其是普通水位下基质吸力分布的精确描述,是非饱和土边坡稳定分析的重要前提。由于基质吸力的实际量测与理论计算方法较为复杂,而土体含水率的量测手段与实验方法更为成熟。根据边坡的含水率分布,通过基质吸力与土体饱和度之间的对应关系(即土水特征曲线)推求边坡基质吸力分布,是获得非饱和土边坡剪切强度的一种有效方法。天然工况下边坡含水率分布曲线也具有非线性特征,根据现场试验结果可以建立边坡不同高度处的含水率分布曲线。文献[11]通过室内试验拟合了不同粒径的土质边坡中初始含水率沿坡高变化的函数关系,并引入了含水率分布系数和相关修正系数来提高含水率在不同土质边坡中分布的准确性,为边坡稳定性的分析提供了试验依据。其函数关系式为:
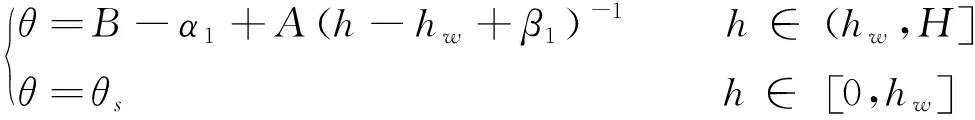
(2)
其中,h为边坡上某点的高度;θ为土体体积含水率;hw为地下水位高度;B为土体自然持水能力;H为边坡总高度;A为含水率分布系数;θs为土体饱和含水率;α1、β1为修正系数,其表达式为:
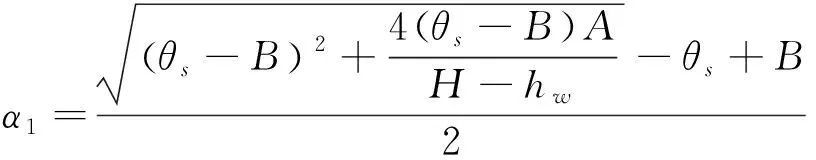
(3)
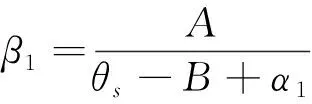
(4)
基于(2)式可以得到土体含水率沿坡高变化的简化模型,三种土体边坡中含水率分布形状相似,均呈现出“L”形分布状态,如图2所示。
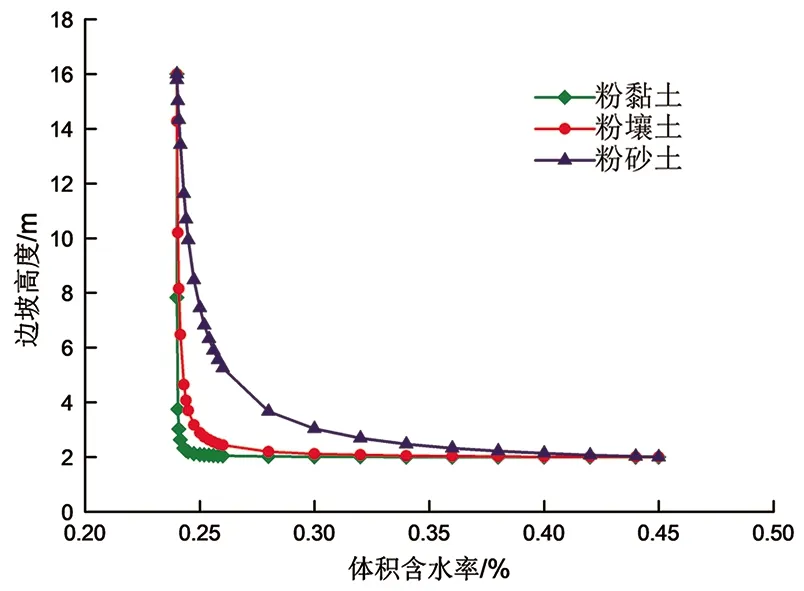
图2 土体含水率随坡高度分布Fig.2 Distribution of soil water content in the slope
1.2 土水特征曲线
非饱和土的基质吸力随土体含水率发生变化,体积含水率和基质吸力的关系曲线称为土水特征曲线(characteristic curve of soil water,SWCC)。常用的土水特征模型包括Van Genuchten模型(VG模型)、Brooks and Corey模型(BC模型)、Fredlund and Xing模型等。BC模型的表达形式相对较简单,但对于颗粒较细的土体通常精度不高。Fredlund and Xing模型和VG模型的应用更为广泛,其中VG模型对非饱和土具有更高的拟合精度[12],因此本文利用VG模型进行土水特征的建模更加合适,其表达式为:
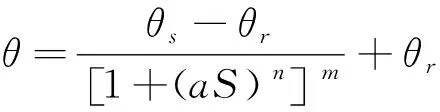
(5)
其中,θ为土体体积含水率;θr为土体残余含水率;θs为土体饱和含水率;S为基质吸力;α、m、n为土水特征曲线的拟合参数,其中,m=1-1/n。
由于土体粒径及矿物成分均不相同,粉黏土、粉壤土、粉砂土的土水特征曲线也具有较大差别。本文在前人对VG模型参数研究的基础之上,选择3种具有代表性的土体[12-14],粉黏土和粉壤土的土水特征曲线较为接近,进气值较高,曲线斜率变化较小,土体持水能力较好;而粉砂土曲线斜率变化趋势较快,持水性能低于粉黏土和粉壤土,其VG土水特征曲线如图3所示。
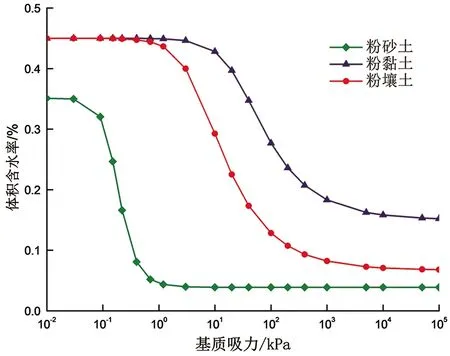
图3 非饱和土-水特征曲线Fig.3 Soil-water characteristic curve of unsaturated soil
2 上限分析离散法的基本原理
2.1 上限分析离散机构生成原理
基于“离散”法的边坡破坏机构示意图,如图4所示。边坡高度为H,地下水位高度为hw,水位线以上ABDE为非饱和区域,水位线以下DCE为饱和区域,边坡坡度为β。本文的破坏机构与传统极限分析法的对数螺旋线滑动面有所不同,滑动面采用“点到点”的方式生成,即离散点Pi+1的位置是由前一个离散点Pi所确定的。滑动面从破趾C处(点P0)开始生成的,并以C点为原点建立直角坐标系。AC为破坏机构的速度间断面,θ0,θh,r0和rh分别为间断面上各点的角度与半径,滑动块体BCA是围绕旋转中心O旋转的刚体,旋转的角速度为ω。在速度间断面下方的土体是静止的,射线OPi和射线OPi+1之间的离散角度为定值δθ,δθ值对边坡稳定性计算的得准确性具有较大影响,δθ值越小,计算精度越高。

图4 离散结构示意图Fig.4 Schematic diagram of discrete structure
假设速度间断面上下均是刚体,破坏机构间断面切向速度v与PiPi+1面速度的夹角为内摩擦角φi,其中速度v遵循相关联流动法则。结合几何关系,通过(6)式可以由点Pi推导出点Pi+1。

(6)
其中,xi和yi是点Pi的横坐标以及纵坐标;xi+1、yi+1是点Pi的横坐标和纵坐标。xo和yo是O横坐标和纵坐标,θi为横轴负方向与射线OPi+1的夹角。
当离散点的纵坐标yi 利用上限分析法对边坡的稳定性进行研究时,计算破坏机构的外力功率以及内能耗散是求解得边坡的稳定性指标关键步骤。文中考虑了基质吸力以及空隙水压力对边坡的影响,因此,破坏机构的总的外力功率等于滑动块体ABC重力功率加上孔隙水压的外力公率;总的内能耗散等于滑动面AC上的内能耗散加上基质吸力的内能耗散。 计算滑动块体ABC的重力功率时,以滑动面AC上相邻的离散点为基础[15],将两相邻的Pi、Pi+1点与B点连接,最后将整个滑动块体分为若干个小的三角形滑动体BPiPi+1,因此整个滑动块的重力功率等于若干小三角形滑动体的重力功率之和: Wγ=-γω∑SiRicosθi (7) 其中,γ为边坡土体的重度;ω为边坡块体的旋转角速度;Si为小三角形滑动块体的面积;Ri为小三角形滑动块体的重心到O点的距离。 当yi (8) 其中,γw为水的重度;hw为地下水位高度;h为滑动面上Pi点的高度,t为滑动面的长度,ru空隙水压力系数;φ为点Pi处的内摩擦角。 当yi≥hw时,机构中空隙水压的外力功率: Ww=0 (9) 则该机构总的外力功率: W=Wγ+Ww (10) 由于滑动块体ABC为刚体,因此只需要计算发生在滑动面AC上耗散的能量,机构的内能耗散即为各直线单元PiPi+1上能量耗散之和: D1=cω∑Liricosφ (11) 其中,c、φ分别为点Pi处的黏聚力和内摩擦角;Li为PiPi+1的长度;ri为O点到点Pi的距离。 当0≤yi≤hw时,滑动面上基质吸力内能耗散率: D2=0 (12) 当hw D2=Sω∑Liricosφ (13) 其中,S为基质吸力,其表达式为: (14) 则该破坏机构总的内能耗散率为: D=D1+D2 (15) 求解安全系数常采用强度折减法,通过将土体的抗剪强度折减,使边坡达到临界破坏状态,折减系数Fs即为边坡安全系数,折减后的抗剪强度参数cf和φf为: (16) 其中,c、φ为原始的抗剪强度参数。 将上限分析与强度折减法相结合进行计算时,可以得到关于安全系数Fs的隐函数,然后对其利用遗传算法进行最优解的搜索计算[16]。同时在本离散机构中,因为外力功率、内能耗散都是通过累积求和的方式得到,Fs的计算还需要结合二分法,优化流程如下: (1)对Fs的搜索范围[Fs1,Fs2]进行设置,令安全系数Fs=(Fs1+Fs1)/2,将其代入(16)式,即可得到cf和φf。 (2)依据上限定理,如果可以搜索到一组θ0和r0解,使min|W-D|<ε,则Fs为上限解。此时令Fs2=Fs,否则,Fs1=Fs。其中,ε为规定阈值,当δθ=0.1o时,ε=5。 (3)重复上述步骤,直到|Fs2-Fs1|<δFs,优化过程结束,得到的Fs即为安全系数的最小上限解。δFs为规定阈值,一般取δFs=0.1。具体Fs的求解过程如图5所示。 图5 安全系数求解流程图Fig.5 Flow chart of safety factor solution 为验证本文模型和所导公式的正确性,将本文的计算结果同已有文献[9]的结果进行对比。基本参数:含水率分布参数A黏=0.5,吸力摩擦角φb=20°,残余含水率θr=0.15,饱和含水率θs=0.45,边坡高度H=20m,有效粘聚力c′=14kPa,有效内摩擦角φ′=27.63°,土体重度γ=19.08kN/m3。结合(2)式和(5)式可以获得基质吸力沿坡高分布的曲线,如图6所示。 图6 基质吸力沿坡高分布的示意图Fig.6 Matrix suction distribution along slope height 本文计算了不同地下水位(2m和6m)和不同坡度(1∶4~1∶1)下边坡安全系数,并将本文计算结果与文献[9]的计算结果进行对比,对比结果如表1所示。从计算结果可以看出,本文结果与文献[9]中假设基质吸力线性分布的安全系数具有良好的一致性,最大误差大仅为8%,充分证明了通过土体含水率掌握基质吸力在边坡中分布形态,进而对边坡稳定性分析是可行的。 表1 不同坡度、地下水位条件下的安全系数对比 为分析边坡坡度、地下水位高度、吸力摩擦角等因素对边坡稳定性的影响,假设本文的非饱和土边坡是均质的。参数取值:边坡表面含水率0.24,含水率分布系数分别是:A黏=0.1,A壤=0.01,A砂=0.001,土体重度γ=20kN/m3。并分析了3种不同粒径的土体边坡在稳定性方面的差异。 4.1.1 模拟结果及工况β是影响边坡稳定性的重要指标,为了解坡度对边坡稳定性的影响机理。本文选取粉砂土、粉壤土、粉黏土的c′分别是5、10、14kPa,有效内摩擦角φ′=27°,φb=20°,坡度β从25°递增到50°。在上述参数下计算了水位hw=2m和hw=5m时的安全系数,计算结果如图7所示。 图7 安全系数-坡度-水位曲线Fig.7 The safety factor-gradient-water level curve 4.1.2 参数分析 不同地下水位,3种土体边坡安全系数Fs与坡度β的关系如图7所示。由图7可知,两种不同水位下,边坡安全系数Fs变化规律较为相似,地下水位hw和坡度β对边坡的Fs影响较大。当处于同一坡度β,同一地下水位hw时,对比3种土体边坡的安全系数可以发现:粉黏土边坡稳定性最佳、粉砂土边坡稳定性最差、粉壤土边坡在两者之间。当地下水位发生变化时,粉黏土边坡和粉壤土边坡的安全性系数降低幅度较粉砂土大。例如,坡度β=40°,水位从2m升高至5m时,粉黏土边坡和粉壤土边坡的安全系数平均降低幅度超过8.5%,而粉砂土边坡的安全系数降低幅度低于6%。 对于不同土体的非饱和边坡,Fs值与坡度β值之间存在非线性的变化关系。随着坡度增大,边坡安全系数显著降低,并且变化速率逐渐降低。以地下水位hw=2m的粉黏土边坡为例,当坡度从β在25°到30°之间时,边坡平均安全系数Fs≈1.52,安全系数的变化速率为0.0457;而当β升高到45°到50°之间时,边坡平均安全系数Fs≈0.9483,安全系数变化速率为0.0211。因此在实际工程中边坡坡度对边坡安全性的影响也是不容忽视的。 4.2.1 模拟结果及工况 吸力摩擦角φb反映抗剪强度随基质吸力增加的速率,是非饱和土抗剪强度的重要指标,因此有必要考察不同取值对边坡安全系数的影响。研究选取粉砂土、粉壤土、粉黏土的c′分别是5、10、14kPa,有效内摩擦角φ′=27°,地下水位高度hw=2m,吸力摩擦角φb从10°变化到27°,基于以上条件分别计算坡度β=30°和β=45°时的安全系数,计算结果如图8所示。 图8 安全系数-吸力摩擦角-坡度曲线Fig.8 The safety factor-angle of suction friction-gradient curve 4.2.2 参数分析 从图8可知,在不同坡度情况下,三种土体边坡的安全系数都随着吸力摩擦角的增大而增加。观察不同土体边坡在不同坡角下,吸力摩擦角对边坡稳定性影响因土壤类型而异。当吸力摩擦角φb取较小值,坡度β分别取值30°和45°时,三种土体边坡的Fs降低了约0.2;而随着吸力摩擦角的不断增大,两坡度下Fs的差值也在不断增加,其中粉黏土边坡的Fs下降最多,在φb=φ′时,安全系数Fs降低约0.56。 研究采用了线性的非饱和强度公式,将吸力摩擦角取值为常数,观察图8可知,同一坡度,同一土体时,吸力摩擦角的取值大小对边坡的稳定性具有较大的影响,以粉黏土为例,当φb=10°时,边坡安全系数Fs=0.8965,当φb=27°时,边坡安全系数Fs=1.7920,安全系数相差较大。因此对于实际工程中的边坡,非饱和强度对边坡安全系数的影响较为显著,在设计时对于土体φb的取值应给予充分考虑。 4.3.1 模拟结果及工况 在影响非饱和土边坡滑动的各种外界的因素中,地下水位对边坡的安全稳定性具有显著的影响作用,为突出地下水位对边坡稳定性的影响。研究选取粉砂土、粉壤土、粉黏土的c′分别是5、10、14kPa,有效内摩擦角φ′=27°,φb=20°,地下水位hw从1m上升到10m。基于以上条件分别计算坡度β=30°和β=45°时的安全系数,计算结果如图9所示。 图9 安全系数-地下水位-坡度曲线Fig.9 The safety factor-ground water level-gradient curve 4.3.2 参数分析 不同粒径土体边坡安全系数Fs与地下水位hw的关系如图9所示。在不同坡度情况下,三种粒径的土体边坡安全系数都随着地下水位的升高而减小。以β=30°的粉壤土边坡为例,当地下水位hw=1m时,安全系数Fs=1.1999;hw=10m时,安全系数Fs=0.8778,安全系数降低了27%,边坡处于失稳状态。 产生上述现象的原因有两种,一是水位上升导致部分边坡土体由非饱和状态转变至饱和状态,边坡非饱和区域面积减小,同时非饱和区内部的含水率显著增大,造成边坡内部基质吸力持续降低,总抗剪强度显著下降;二是随着地下水位升高,原饱和区内部土体的孔隙水压持续增大,土体有效应力下降,也导致边坡抗剪强度降低。 从图9可以看出,在低水位的情况下,地下水位变化对边坡安全系数的影响更加敏感;在高水位时,地下水位的变化对边坡安全系数影响较小,以β=30°的粉黏土边坡为例,当地下水位hw=1m,Fs=1.5599;hw=4m,Fs=1.2188,平均地下水位每升高1m,安全系数降低0.1137;而当地下水位hw由7m升高至10m时,平均地下水位每升高1m,安全系数降低0.0315。由此可见,处于初始地下水位较低的边坡,地下水位的骤然升高,将对边坡的稳定性产生较大影响。 本文从非饱和土边坡的含水率分布出发得到基质吸力分布曲线,基于极限分析上限模型,讨论了不同非饱和土边坡的稳定性问题,研究了地下水位、边坡坡度以及吸力摩擦角对边坡稳定性的影响。根据计算结果,可以得出以下结论: (1)通过含水率分布曲线与土水特征模型的拟合获得了较为精确的吸力曲线,不同的微观土性参数可以获得不同的吸力曲线,不同曲线之间的差异表征了边坡中基质吸力的变化。土体含水率以及相关土性参数对土质边坡的稳定性具有重要影响,应在边坡设计、施工中充分考虑其影响。 (2)本文从坡度、吸力摩擦角,地下水位高度这三个方面研究了非饱和土边坡的失稳特点,研究表明它们与边坡安全系数之间存在一定的变化规律。其中,随着β的增加,安全系数降低的同时,β的变化对稳定性的影响逐渐减小;当φb的增加,Fs近乎均匀增长;当hw处于浅水位时,地下水位变化对边坡稳定性影响较大,hw增长至较高水位时,地下水位变化对边坡稳定性影响较小。 (3)边坡稳定性受多种因素的影响,β和φb是从边坡的几何形态以及土体强度直接对稳定性产生影响,坡度越陡稳定性越低,由抗剪强度理论可知,φb越大稳定性越高;而hw变化时边坡安全系数变化规律相对较复杂,是因为地下水位的变化先对边坡内基质吸力产生影响,水位上升,基质吸力降低或消失,使得土体抗剪强度降低,边坡稳定性降低;反之,则边坡稳定性得到提高。2.2 能耗计算

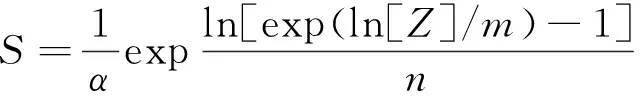

2.3 安全系数优化计算

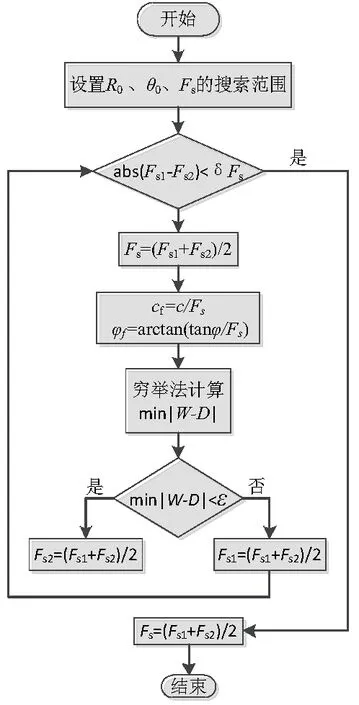
3 对比验证

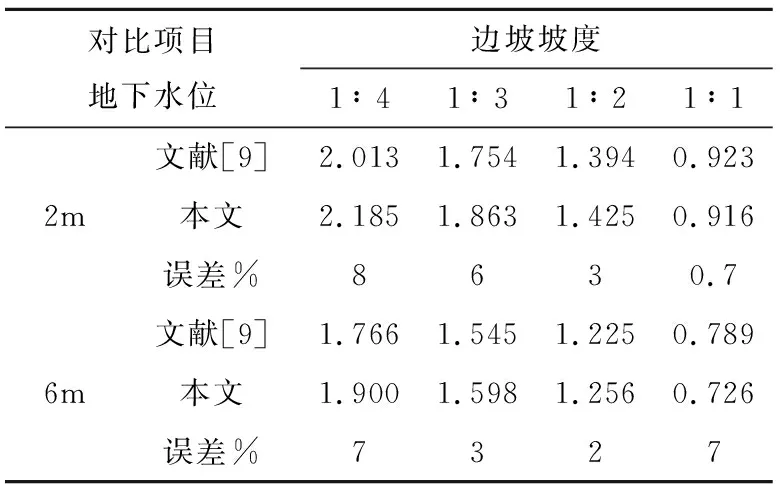
4 模拟结果和参数分析
4.1 不同地下水位时β对安全系数的影响

4.2 不同坡度时φb对安全系数的影响
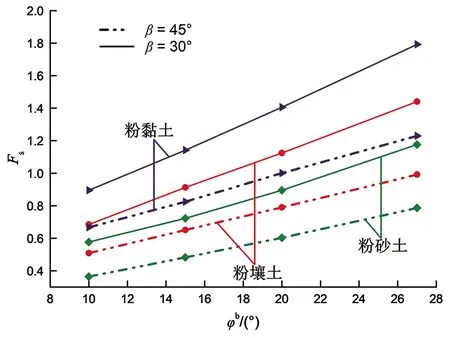
4.3 不同坡度时hw对安全系数的影响

5 结论
